8.8: Applications
- Page ID
- 60050
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The Five-Step Method
We are now in a position to study some applications of rational equations. Some of these problems will have practical applications while others are intended as logic developers.
We will apply the five-step method for solving word problems.
Five-Step Method
- Represent all unknown quantities in terms of x or some other letter.
- Translate the verbal phrases to mathematical symbols and form an equation.
- Solve this equation.
- Check the solution by substituting the result into the original statement of the problem.
- Write the conclusion.
Remember, step 1 is very important: always
Introduce a variable.
Sample Set A
When the same number is added to the numeartor and denominator of the fraction \(\dfrac{3}{5}\), the result if \(\dfrac{7}{9}\). What is the number that is added?
Step 1: Let \(x = \) the number being added.
\(\begin{array}{flushleft}
\text{Step 2: } & \dfrac{3+x}{5+x} &= \dfrac{7}{9}\\
\text{Step 3: } & \dfrac{3+x}{5+x} &= \dfrac{7}{9} & \text{An excluded value is } -5\\
&&& \text{ Multiply each term by } 9(5 + x)\\
& 9(5 + x) \cdot \dfrac{3 + x}{5 + x} &= 9(5 + x) \cdot \dfrac{7}{9}\\
& 9(3 + x) &= 7(5 + x)\\
& 27 + 9x &= 35 + 7x\\
& 2x &=8\\
& x &= 4 & \text{ Check this potential solution }\\
\text{Step 4: } & \dfrac{3 + 4}{5 + 4} &= \dfrac{7}{9} & \text{ Yes, this is correct }\\
\text{Step 5: The number added is } 4
\end{array}\)
Practice Set A
The same number is added to the numerator and denominator of the fraction \(\dfrac{4}{9}\). The result is \(\dfrac{2}{3}\). What is the number that is added?
Step 1: Let \(x =\)
Step 2:
Step 3:
Step 4:
Step 5: The number added is __.
- Answer
-
The number added is 6.
Sample Set B
Two thirds of a number added to the reciprocal of the number yields \(\dfrac{25}{6}\). What is the number?
Step 1: Let \(x = \) the number.
Step 2: Recall that the reciprocal of a number \(x\) is the number \(\dfrac{1}{x}\).
\(\dfrac{2}{3} \cdot x + \dfrac{1}{x} = \dfrac{25}{6}\)
\(\begin{array}{flushleft}
\text{Step 3: } & \dfrac{2}{3} \cdot x + \dfrac{1}{x} &= \dfrac{25}{6} & \text{ The LCD is } 6x \text{. Multiply eeach term by } 6x\\
& 6x \cdot \dfrac{2}{3}x + 6x \cdot \dfrac{1}{x} &= 6x \cdot \dfrac{25}{6}\\
& 4x^2 + 6 &= 25x & \text{ Solve this nonfractional quadratic equation to obtain the potential solutions. (Use the zero-factor property.)\\
& 4x^2 - 25x + 6 &= 0\\
& (4x - 1)(x - 6) &= 0\\
& x &= \dfrac{1}{4}, 6 & \text{ Check these potential solutions }
\end{array}\)
Step 4: Substituting into the original equation, it can be that both solutions check.
Step 5: There are two solutions: \(\dfrac{1}{4}\) and \(6\).
Practice Set B
Seven halves of a number added to the reciprocal of the number yields \(\dfrac{23}{6}\). What is the number?
Step 1: Let \(x =\)
Step 2:
Step 3:
Step 4:
Step 5: The number is .
- Answer
-
There are two numbers: \(\dfrac{3}{7}, \dfrac{2}{3}\)
Sample Set C
Person A, working alone, can pour a concrete walkway in 6 hours. Person B, working alone, can pour the same walkway in 4 hours. How long will it take both people to pour the concrete walkway working together?
Step 1: Let \(x = \) the number of hours to pour the concrete walkway working together (since this is what we’re looking for).
Step 2: If person A can complete the job in 6 hours, A can complete \(\dfrac{1}{6}\) of the job in 1 hour. If person B can complete the job in 4 hours, B can complete \(\dfrac{1}{4}\) of the job in 1 hour. If A and B, working together, can complete the job in \(x\) hours, they can complete \(\dfrac{1}{x}\) of the job in 1 hour. Putting these three facts into equation form, we have:
\(\dfrac{1}{6} + \dfrac{1}{4} = \dfrac{1}{x}\)
\(\begin{array}{flushleft}
\text{Step 3: } & \dfrac{1}{6} + \dfrac{1}{4} &= \dfrac{1}{x} & \text{ An excluded value is 0}\\
& 12x \cdot \dfrac{1}{6} + \dfrac{12x} \cdot \dfrac{1}{4} &= 12x \cdot \dfrac{1}{x}\\
& 2x + 3x &= 12 & \text{ Solve this nonfractional equation to obtain the potential solutions}\\
& 5x &= 12\\
& x &=\dfrac{12}{5} \text{or} x=2\dfrac{2}{5} & \text{ Check this potential solution. }\\
\text{ Step 4: } & \dfrac{1}{6} + \dfrac{1}{4} &= \dfrac{1}{x}\\
& \dfrac{1}{6} + \dfrac{1}{4} = \dfrac{\frac{1}{12}}{5}. & \text{ Is this correct? }\\
& \dfrac{1}{6} + \dfrac{1}{4} &= \dfrac{5}{12} & \text{ The LCD is } 12 \text{. Is this correct? }\\
& \dfrac{2}{12} + \dfrac{3}{12} &= \dfrac{5}{12} & \text{ Is this correct? }\\
& \dfrac{5}{12} &= \dfrac{5}{12} & \text{Yes, this is correct}
\end{array}\)
Step 5: Working together, A and B can pour the concrete walkway in \(2\dfrac{2}{5}\) hours.
Practice Set C
Person A, working alone, can pour a concrete walkway in 9 hours. Person B, working alone, can pour the same walkway in 6 hours. How long will it take both people to pour the concrete walkway working together?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5: Working together, A and B .
- Answer
-
Working together, A and B can pour the concrete walkway in \(3\dfrac{3}{5}\) hr.
Sample Set D
An inlet pipe can fill a water tank in 12 hours. An outlet pipe can drain the tank in 20 hours. If both pipes are open, how long will it take to fill the tank?
Step 1: Let x = the number of hours required to fill the tank.
Step 2: If the inlet pipe can fill the tank in \(12\) hours, it can fill \(\dfrac{1}{12}\) of the tank in \(1\) hour.
If the outlet pipe can drain the tank in 20 hours, it can drain \(\dfrac{1}{20}\) of the tank in \(1\) hour.
If both pipes are open, it takes \(x\) hours to fill the tank. So \(\dfrac{1}{x}\) of the tank will be filled in \(1\) hour.
Since water is being added (inlet pipe) and subtracted (outlet pipe) we get
\(\dfrac{1}{12} - \dfrac{1}{20} = \dfrac{1}{x}\)
\(\begin{array}{flushleft}
\text{Step 3: }& \dfrac{1}{12} - \dfrac{1}{20} &= \dfrac{1}{x} & \text{ An excluded value is } 0 \text{. The LCD is } 60x \text{. Multiply each term by } 60x.\\
& 60x \cdot \dfrac{1}{12} - 60x \cdot \dfrac{1}{20} &= 60x \cdot \dfrac{1}{x}\\
& 5x - 3x &= 60 & \text{ Solve this nonfractional equation to obtain the potential solutions. }\\
& 2x &= 60\\
& x &= 30 & \text{ Check this potential solution }\\
\text{Step 4: } & \dfrac{1}{12} - \dfrac{1}{20} &= \dfrac{1}{x}\\
& \dfrac{1}{12} - \dfrac{1}{20} &= \dfrac{1}{30} & \text{ The LCD is } 60 \text{. Is this correct? }\\
& \dfrac{5}{60} - \dfrac{3}{60} &= \dfrac{1}{30} & \text{ Is this correct? }\\
& \dfrac{1}{30} &= \dfrac{1}{30} & \text{ Yes, this is correct }
\end{array}\)
Step 5: With both pipes open, it will take \(30\) hours to fill the water tank.
Practice Set D
An inlet pipe can fill a water tank in 8 hours and an outlet pipe can drain the tank in 10 hours. If both pipes are open, how long will it take to fill the tank?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
- Answer
-
It will take 40 hr to fill the tank.
Sample Set E
It takes person A 3 hours longer than person B to complete a certain job. Working together, both can complete the job in 2 hours. How long does it take each person to complete the job working alone?
Step 1: Let \(x=\) time required for B to complete the job working alone. Then, \((x+3) =\) time required for A to complete the job working alone.
\(\begin{array}{flushleft}
\text{Step 2: } & \dfrac{1}{x} + \dfrac{1}{x+3} &= \dfrac{1}{2}\\
\text{Step 3: } & \dfrac{1}{x} + \dfrac{1}{x+3} &= \dfrac{1}{2} & \text{ The two excluded values are } 0 \text{ and } -3 \text{. The LCD is } 2x(x+3)\\
& 2x(x+3) \cdot \dfrac{1}{x} + 2x(x+3) \cdot \dfrac{1}{x+3} &= 2x(x+3) \cdot \dfrac{1}{2}\\
& 2(x+3) + 2x &= x(x+3)\\
& 2x + 6 + 2x &= x^2 + 3x & \text{This is a quadratic equation that can be solved using the zero-factor property}\\
& 4x + 6 &= x^2 + 3x\\
& x^2 - x - 6 &= 0\\
& (x-3)(x+2) &= 0\\
& (x-3)(x+2) &= 0\\
& x &= 3, -2 & \text{Check these potential solutions}
\end{array}\)
Step 4: If \(x = -2\), the equation checks, but does not even make physical sense.
If \(x = 3\), the equation checks
\(x = 3\) and \(x + 3 = 6\).
Step 5: Person B can do the job in \(3\) hours and person A can do the job in \(6\) hours.
Practice Set E
It takes person A 4 hours less than person B to complete a certain task. Working together, both can complete the task in \(\dfrac{8}{3}\) hours. How long does it take each person to complete the task working alone?
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
- Answer
-
Person A, 4 hr to complete the task; person B, 8 hr complete the task.
Sample Set F
The width of a rectangle is \(\dfrac{1}{3}\) its length. Find the dimensions (length and width) if the permieter is \(16\) cm.
Step 1: Let \(x=\) length. Then \(\dfrac{x}{3}=\) width.
Step 2: Make a sketch of the rectangle.
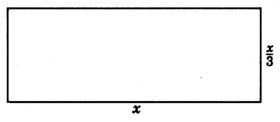
The perimeter of a figure is the total length around the figure.
\(\begin{array}{flushleft}
& x + \dfrac{x}{3} + x + \dfrac{x}{3} &= 16\\
& 2x + \dfrac{2x}{3} &= 16\\
\text{Step 3: } & 2x + \dfrac{2x}{3} &= 16 & \text{The LCD is } 3\\
& 3 \cdot 2x + 3 \cdot \dfrac{2x}{3} &= 3 \cdot 16\\
& 6x + 2x &= 48\\
& 8x &= 48\\
& x &= 6 & \text{ Check this potential solution. }\\
\text{Step 4: } & 6 + \dfrac{6}{3} + 6 + \dfrac{6}{3} &= 16 & \text{Is this correct?}
& 6 + 2 + 6 + 2 &= 16 & \text{Is this correct?}\\
& 16 &= 16 & \text{Yes, this is correct.}
\end{array}\)
Since \(x = 6, \dfrac{x}{3} = \dfrac{6}{3} = 2\)
Step 5: The length\(=6\)cm and the width\(=2\)cm.
Practice Set F
The width of a rectangle is \(\dfrac{1}{12}\) its length. Find the dimensions (length and width) if the perimeter is \(78\) feet.
Step 1:
Step 2:
Step 3:
Step 4:
Step 5:
- Answer
-
length = 36 ft, width = 3 ft.
Exercises
For the following problems, solve using the five-step method.
When the same number is added to both the numerator and denominator of the fraction \(\dfrac{3}{7}\), the result is \(\dfrac{2}{3}\). What is the number?
- Answer
-
The number added is \(5\).
When the same number is added to both the numerator and denominator of the fraction \(\dfrac{5}{8}\), the result is \(\dfrac{3}{4}\). What is the number?
When the same number is added to both the numerator and denominator of the fraction \(\dfrac{3}{8}\), the result is \(\dfrac{1}{6}\). What is the number?
- Answer
-
The number added is \(−2\).
When the same number is added to both the numerator and denominator of the fraction \(\dfrac{7}{9}\), the result is \(\dfrac{2}{3}\). What is the number?
When the same number is subtracted to both the numerator and denominator of the fraction \(\dfrac{1}{10}\), the result is \(\dfrac{2}{3}\). What is the number?
- Answer
-
The number subtracted is \(−17\).
When the same number is subtracted to both the numerator and denominator of the fraction \(\dfrac{3}{4}\), the result is \(\dfrac{5}{6}\). What is the number?
One-third of a number added to the reciprocal of number yields \(\dfrac{13}{6}\). What is the number?
- Answer
-
\(x= \dfrac{1}{2}, 6\)
Four-fifths of a number added to the reciprocal of number yields \(\dfrac{81}{10}\). What is the number?
One-half of a number added to twice the reciprocal of the number yields \(2\). What is the number?
- Answer
-
\(2\)
One-fourth of a number added to four times the reciprocal of the number yields \(\dfrac{-10}{3}\). What is the number?
One inlet pipe can fill a tank in 8 hours. Another inlet pipe can fill the tank in 5 hours. How long does it take both pipes working together to fill the tank?
- Answer
-
\(3\dfrac{1}{13}\) hours.
One pipe can drain a pool in 12 hours. Another pipe can drain the pool in 15 hours. How long does it take both pipes working together to drain the pool?
A faucet can fill a bathroom sink in 1 minute. The drain can empty the sink in 2 minutes. If both the faucet and drain are open, how long will it take to fill the sink?
- Answer
-
two minutes
A faucet can fill a bathtub in \(6\dfrac{1}{2}\) minutes. The drain can empty the tub in \(8\dfrac{1}{3}\) minutes. If both the faucet and drain are open, how long will it take to fill the bathtub?
An inlet pipe can fill a tank in 5 hours. An outlet pipe can empty the tank in 4 hours. If both pipes are open, can the tank be filled? Explain.
- Answer
-
No. \(x=−20\) hours.
An inlet pipe can fill a tank in \(a\) units of time. An outlet pipe can empty the tank in \(b\) units of time. If both pipes are open, how many units of time are required to fill the tank? Are there any restrictions on \(a\) and \(b\) ?
A delivery boy, working alone, can deliver all his goods in 6 hours. Another delivery boy, working alone, can deliver the same goods in 5 hours. How long will it take the boys to deliver all the goods working together?
- Answer
-
\(2\dfrac{8}{11}\) hours.
A Space Shuttle astronaut can perform a certain experiment in 2 hours. Another Space Shuttle astronaut who is not as familiar with the experiment can perform it in \(2\dfrac{1}{2}\) hours. Working together, how long will it take both astronauts to perform the experiment?
One person can complete a task 8 hours sooner than another person. Working together, both people can perform the task in 3 hours. How many hours does it take each person to complete the task working alone?
- Answer
-
First person: 12 hours; second person: 4 hours
Find two consecutive integers such that two thirds of the smaller number added to the other yields 11.
Find two consecutive integers such that three fourths of the smaller number added to the other yields 29.
- Answer
-
16,17
The width of a rectangle is \(\dfrac{2}{5}\) its length. Find the dimensions if the perimeter is 42 meters.
The width of a rectangle is \(\dfrac{3}{7}\) the length. Find the dimensions if the perimeter is 60 feet.
- Answer
-
width=9 ft; length=21 ft
Two sides of a triangle have the same length. The third side is twice as long as either of the other two sides. The perimeter of the triangle is 56 inches. What is the length of each side?
In a triangle, the second side is 3 inches longer than first side. The third side is \(\dfrac{3}{4}\) the length of the second side. If the perimeter is 30 inches, how long is each side?
- Answer
-
side 1=9 inches; side 2=12 inches; side 3=9 inches
he pressure due to surface tension in a spherical drop of liquid is given by \(P=\dfrac{2T}{r}\), where \(T\) is the surface tension of the liquid and \(r\) is the radius of the drop. If the liquid is a bubble, it has two surfaces and the surface tension is given by
\(P = \dfrac{2T}{r} + \dfrac{2T}{r} = \dfrac{4T}{r}\)
(a) Determine the pressure due to surface tension within a soap bubble of radius 2 inches and surface tension 28.
(b) Determine the radius of a bubble if the pressure due to surface tension is 52 and the surface tension is 39.
The equation \(\dfrac{1}{p} + \dfrac{1}{q} = \dfrac{1}{f}\) relates the distance \(p\) of an object from a lens and the image distance \(q\) from the lens to the focal length \(f\) of the lens.
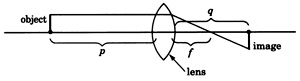
(a) Determine the focal length of a lens in which an object 10 feet away produces an image 6 feet away.
(b) Determine how far an object is from a lens if the focal length of the lens is 6 inches and the image distance is 10 inches.
(c) Determine how far an image will be from a lens that has a focal length of \(4\dfrac{4}{5}\) cm and the object is 12 cm away from the lens.
- Answer
-
a) \(f = \dfrac{15}{4}\) ft.
b) \(p = 15\) inches.
c) \(q = 8\) cm.
Person A can complete a task in 4 hours, person B can complete the task in 6 hours, and person C can complete the task in 3 hours. If all three people are working together, how long will it take to complete the task?
Three inlet pipes can fill a storage tank in 4, 6, and 8 hours, respectively. How long will it take all three pipes to fill the tank?
- Answer
-
\(1\dfrac{11}{13}\) hours
An inlet pipe can fill a tank in 10 hours. The tank has two drain pipes, each of which can empty the tank in 30 hours. If all three pipes are open, can the tank be filled? If so, how long will it take?
An inlet pipe can fill a tank in 4 hours. The tank has three drain pipes. Two of the drain pipes can empty the tank in 12 hours, and the third can empty the tank in 20 hours. If all four pipes are open, can the tank be filled? If so, how long will it take?
- Answer
-
30 hours
Exercises For Review
Factor \(12a^2 + 13a - 4\).
Find the slope of the line passing through the points \((4, -3)\) and \((1, -6)\).
- Answer
-
\(m=1\)
Find the quotient: \(\dfrac{2 x^{2}-11 x-6}{x^{2}-2 x-24} \div \dfrac{2 x^{2}-3 x-2}{x^{2}+2 x-8}\)
Find the difference: \(\dfrac{x+2}{x^{2}+5 x+6}-\dfrac{x+1}{x^{2}+4 x+3}\)
- Answer
-
\(0\)
Solve the equation \(\dfrac{9}{2m-5} = -2\)


