8.10: Dividing Polynomials
- Page ID
- 60052
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dividing A Polynomial By A Monomial
The following examples illustrate how to divide a polynomial by a monomial. The division process is quite simple and is based on the addition of rational expressions.
\(\dfrac{a}{c} + \dfrac{b}{c} = \dfrac{a+b}{c}\)
Turning this equation around we get
\(\dfrac{a+b}{c} = \dfrac{a}{c} + \dfrac{b}{c}\)
Now we simply divide \(c\) into \(a\), and \(c\) into \(b\). This should suggest a rule.
To divide a polynomial by a monomial, divide every term of the polynomial by the monomial.
Sample Set A
\(\dfrac{3x^2 + x - 11}{x}\). Divide every term of \(3x^2 + x - 11\) by \(x\).
\(\dfrac{3x^2}{x} + \dfrac{x}{x} - \dfrac{11}{x} = 3x + 1 - \dfrac{11}{x}\)
\(\dfrac{8x^3 + 4a^2 - 16a + 9}{2a^2}. Divide every term of \(8a^3 + 4a^2 - 16a + 9\) by \(2a^2\).
\(\dfrac{4b^6 - 9b^4 - 2b + 5}{-4b^2}\). Divide every term of \(4b^6 - 9b^4 - 2b + 5\) by \(-4b^2\).
\(\dfrac{4b^6}{-4b^2} - \dfrac{9b^4}{-4b^2} - \dfrac{2b}{-4b^2} + \dfrac{5}{-4b^2} = -b^4 + \dfrac{9}{4}b^2 + \dfrac{1}{2b} - \dfrac{5}{4b^2}\)
Practice Set A
Perform the following divisions.
\(\dfrac{2x^2 + x - 1}{x}\)
- Answer
-
\(2x + 1 - \dfrac{1}{x}\)
\(\dfrac{3x^3 + 4x^2 + 10x - 4}{x^2}\)
- Answer
-
\(3x + 4 + \dfrac{10}{x} - \dfrac{4}{x^2}\)
\(\dfrac{a^2b + 3ab^2 + 2b}{ab}\)
- Answer
-
\(a + 3b + \dfrac{2}{a}\)
\(\dfrac{14x^2y^2 - 7xy}{7xy}\)
- Answer
-
\(2xy−1\)
\(\dfrac{10m^3n^2 + 15m^2n^3 - 20mn}{-5m}\)
- Answer
-
\(-2m^2n^2 - 3mn^3 + 4n\)
The Process Of Division
In Section 8.3 we studied the method of reducing rational expressions. For example, we observed how to reduce an expression such as
\(\dfrac{x^2 - 2x - 8}{x^2 - 3x - 4}\)
Our method was to factor both the numerator and denominator, then divide out common factors.
\(\dfrac{(x-4)(x+2)}{(x-4)(x+1)}\)
\(\dfrac{\cancel{(x-4)}(x+2)}{\cancel{(x-4)}(x+1)}\)
\(\dfrac{x+2}{x+1}\)
When the numerator and denominator have no factors in common, the division may still occur, but the process is a little more involved than merely factoring. The method of dividing one polynomial by another is much the same as that of dividing one number by another. First, we’ll review the steps in dividing numbers.
\(\dfrac{35}{8}\). We are to divide 35 by 8.
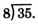We try 4, since 32 divided by 8 is 4.
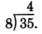Multiply 4 and 8
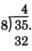Subtract 32 from 35
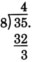Since the remainder 3 is less than the divisor 8, we are done with the 32 division.
\(4\dfrac{3}{8}\). The quotient is expressed as a mixed number.
The process was to divide, multiply, and subtract.
Review Of Subtraction Of Polynomials
A very important step in the process of dividing one polynomial by another is the subtraction of polynomials. Let’s review the process of subtraction by observing a few examples.
1. Subtract \(x -2\) from \(x-5\); that is, find \((x-5) - (x-2)\).
Since \(x-2\) is preceded by a minus sign, remove the parentheses, change the sign of each term, then add.
\(\begin{array}{flushleft}
x-5 && x-5\\
-(x-2) && -x+2\\
\text{_______} & = & \text{_______}\\
&&-3
\end{array}\)
The result is \(-3\)
2. Subtract \(x^3 + 3x^2\) from \(x^3 + 4x^2 + x - 1\).
Since \(x^3 + 3x^2\) is preceded by a minus sign, remove the parentheses, change the sign of each term, then add.
\(\begin{array}{flushleft}
x^3 + 4x^2 + x - 1 && x^3 + 4x^2 + x - 1\\
-(x^3 + 3x^2) && -x^3 - 3x^2\\
\text{_______________} & = & \text{_______________}\\
&&x^2 + x - 1
\end{array}\)
The result is \(x^2 + x - 1\)
3. Subtract \(x^2 + 3x\) from \(x^2 + 1\)
We can write \(x^2 + 1\) as \(x^2 + 0x + 1\).
\(\begin{array}{flushleft}
x^2 + 1 && x^2 + 0x + 1 && x^2 + 0x + 1\\
-(x^2 + 3x) && -(x^2 + 3x) && -x^2 - 3x\\
\text{____________} & = & \text{____________} & = & \text{____________}\\
&&&& -3x + 1
\end{array}\)
Dividing A Polynomial By A Polynomial
Now we’ll observe some examples of dividing one polynomial by another. The process is the same as the process used with whole numbers: divide, multiply, subtract, divide, multiply, subtract,....
The division, multiplication, and subtraction take place one term at a time. The process is concluded when the polynomial remainder is of lesser degree than the polynomial divisor.
Sample Set B
Perform the division.
\(\dfrac{x-5}{x-2}\). We are to divide \(x-5\) by \(x-2\).
\(1 - \dfrac{3}{x-2}\)
Thus,
\(\dfrac{x-5}{x-2} = 1 - \dfrac{3}{x-2}\)
\(\dfrac{x^3 + 4x^2 + x - 1}{x + 3}\). We are to divide \(x^3 + 4x^2 + x - 1\) by \(x + 3\).
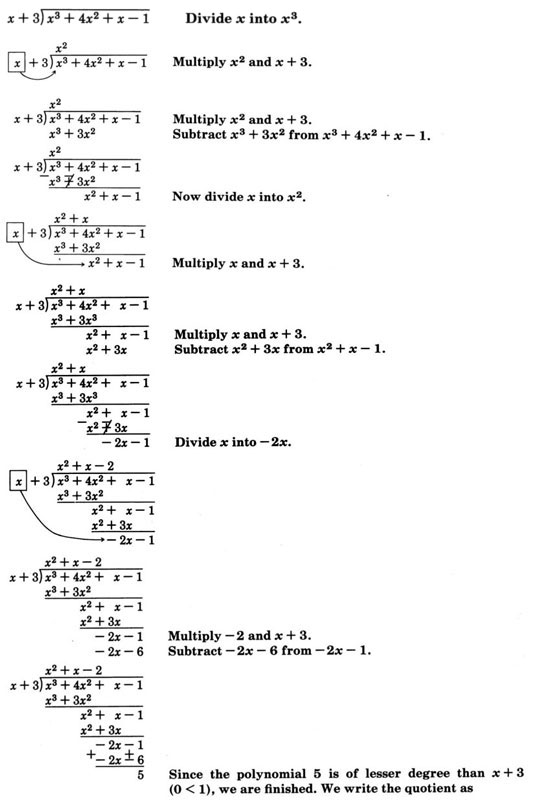
\(x^2 + x - 2 + \dfrac{5}{x+3}\)
Thus,
\(\dfrac{x^3 + 4x^2 + x - 1}{x + 3} = x^2 + x - 2 + \dfrac{5}{x+3}\)
Practice Set B
Perform the following divisions.
\(\dfrac{x+6}{x-1}\)
- Answer
-
\(1 + \dfrac{7}{x-1}\)
\(\dfrac{x^2 + 2x + 5}{x + 3}\)
- Answer
-
\(x - 1 + \dfrac{8}{x+3}\)
\(\dfrac{x^3 + x^2 - x - 2}{x + 8}\)
- Answer
-
\(x^2 - 7x + 55 - \dfrac{442}{x+8}\)
\(\dfrac{x^3 + x^2 - 3x + 1}{x^2 + 4x - 5}\)
- Answer
-
\(x - 3 + \dfrac{14x - 14}{x^2 + 4x - 5} = x - 3 + \dfrac{14}{x+5}\)
Sample Set C
Divide \(2x^3 - 4x + 1\) by \(x + 6\)
\(\dfrac{2x^3 - 4x + 1}{x + 6}\) Notice that the \(x^2\) term in the numerator is missing. We can avoid any confusion by writing
\(\dfrac{2x^3 + 0x^2 - 4x + 1}{x+6}\) Divide, multiply, and subtract.
\(\dfrac{2x^3 - 4x + 1}{x + 6} = 2x^3 - 12x + 68 - \dfrac{407}{x + 6}\)
Practice Set C
Perform the following divisions.
\(\dfrac{x^2 - 3}{x+2}\)
- Answer
-
\(x - 2 + \dfrac{1}{x+2}\)
\(\dfrac{4x^2 - 1}{x-3}\)
- Answer
-
\(4x + 12 + \dfrac{35}{x-3}\)
\(\dfrac{x^3 + 2x + 2}{x-2}\)
- Answer
-
\(x^2 + 2x + 6 + \dfrac{14}{x-2}\)
\(\dfrac{6x^3 + 5x^2 - 1}{2x + 3}\)
- Answer
-
\(3x^2 - 2x + 3 - \dfrac{10}{2x + 3}\)
Exercises
For the following problems, perform the divisions.
\(\dfrac{6a + 12}{2}\)
- Answer
-
\(3a+6\)
\(\dfrac{12b - 6}{3}\)
\(\dfrac{8y - 4}{-4}\)
- Answer
-
\(−2y+1\)
\(\dfrac{21a - 9}{-3}\)
\(\dfrac{3x^2 - 6x}{-3}\)
- Answer
-
\(−x(x−2)\)
\(\dfrac{4y^2 - 2y}{2y}\)
\(\dfrac{9a^2 + 3a}{2a}\)
- Answer
-
\(3a+1\)
\(\dfrac{20x^2 + 10x}{5x}\)
\(\dfrac{6x^3 + 2x^2 + 8x}{2x}\)
- Answer
-
\(3x^2 + x + 4\)
\(\dfrac{26y^3 + 13y^2 + 39y}{13y}\)
\(\dfrac{a^2b^2 + 4a^2b + 6ab^2 - 10ab}{ab}\)
- Answer
-
\(ab+4a+6b−10\)
\(\dfrac{7x^3y + 8x^2y^3 + 3xy^4 - 4xy}{xy}\)
\(\dfrac{5x^3y^3 - 15x^2y^2 + 20xy}{-5xy}\)
- Answer
-
\(-x^2y^2 + 3xy - 4\)
\(\dfrac{4a^2b^3 - 8ab^4 + 12ab^2}{-2ab^2}\)
\(\dfrac{6a^2y^2 + 12a^2y + 18a^2}{24a^2}\)
- Answer
-
\(\dfrac{1}{4}y^2 + \dfrac{1}{2}y + \dfrac{3}{4}\)
\(\dfrac{3c^3y^3 + 99c^3y^4 - 12c^3y^5}{3x^3y^3}\)
\(\dfrac{16ax^2 - 20ax^3 + 24ax^4}{6a^4}\)
- Answer
-
\(\dfrac{8x^2 - 10x^3 + 12x^4}{3a^3}\) or \(\dfrac{12x^4 - 10x^3 + 8x^2}{3a^2}\)
\(\dfrac{21ay^3 - 18ay^2 - 15ay}{6ay^2}\)
\(\dfrac{-14b^2c^2 + 21b^3 - 28c^3}{-7a^2c^3}\)
- Answer
-
\(\dfrac{2b^2 - 3b^3c + 4c}{a^2c}\)
\(\dfrac{-30a^2b^4 - 35a^2b^3 - 25a^2}{-5b^3}\)
\(\dfrac{x+6}{x-2}\)
- Answer
-
\(1 + \dfrac{8}{x-2}\)
\(\dfrac{y + 7}{y + 1}\)
\(\dfrac{x^2 - x + 4}{x + 2}\)
- Answer
-
\(x - 3 + \dfrac{10}{x+2}\)
\(\dfrac{x^2 + 2x - 1}{x + 1}\)
\(\dfrac{x^2 - x + 3}{x + 1}\)
- Answer
-
\(x - 2 + \dfrac{5}{x + 1}\)
\(\dfrac{x^2 + 5x + 5}{x + 5}\)
\(\dfrac{x^2 - 2}{x + 1}\)
- Answer
-
\(x - 1 - \dfrac{1}{x+1}\)
\(\dfrac{a^2 - 6}{a + 2}\)
\(\dfrac{y^2 + 4}{y + 2}\)
- Answer
-
\(y - 2 + \dfrac{8}{y + 2}\)
\(\dfrac{x^2 + 36}{x + 6}\)
\(\dfrac{x^3 - 1}{x + 1}\)
- Answer
-
\(x^2 - x + 1 - \dfrac{2}{x + 1}\)
\(\dfrac{a^3 - 8}{a + 2}\)
\(\dfrac{x^3 + 3x^2 + x - 2}{x-2}\)
- Answer
-
\(x^2 + 5x + 11 + \dfrac{20}{x-2}\)
\(\dfrac{a^3 + 2a^2 - a + 1}{a - 3}\)
\(\dfrac{x^3 + 2x + 1}{x - 3}\)
\(\dfrac{y^3 + 2y^2 + 4}{y + 2}\)
- Answer
-
\(y^2 + y - 2 + \dfrac{8}{y + 2}\)
\(\dfrac{y^3 + 5y^2 - 3}{y - 1}\)
\(\dfrac{x^3 + 3x^2}{x + 3}\)
- Answer
-
\(x^2\)
\(\dfrac{a^2 + 2a}{a + 2}\)
\(\dfrac{x^2 - x - 6}{x^2 - 2x - 3}\)
- Answer
-
\(1 + \dfrac{1}{x + 1}\)
\(\dfrac{a^2 + 5a + 4}{a^2 - a - 2}\)
\(\dfrac{2y^2 + 5y + 3}{y^2 - 3y - 4}\)
- Answer
-
\(2 + \dfrac{11}{y-4}\)
\(\dfrac{3a^2 + 4a + 2}{3a + 4}\)
\(\dfrac{6x^2 + 8x - 1}{3x + 4}\)
- Answer
-
\(2x - \dfrac{1}{3x + 4}\)
\(\dfrac{20y^2 + 15y - 4}{4y + 3}\)
\(\dfrac{4x^3 + 4x^2 - 3x - 2}{2x - 1}\)
- Answer
-
\(2x^2 + 3x - \dfrac{2}{2x - 1}\)
\(\dfrac{9a^3 - 18a^2 8a - 1}{3a - 2}\)
\(\dfrac{4x^4 - 4x^3 + 2x^2 - 2x - 1}{x-1}\)
- Answer
-
\(4x^3 + 2x - \dfrac{1}{x-1}\)
\(\dfrac{3y^4 + 9y^3 - 2y^2 - 6y + 4}{y + 3}\)
\(\dfrac{3y^2 + 3y + 5}{y^2 + y + 1}\)
- Answer
-
\(3 + \dfrac{2}{y^2 + y + 1}\)
\(\dfrac{2a^2 + 4a + 1}{a^2 + 2a + 3}\)
\(\dfrac{8z^6 - 4z^5 - 8z^4 + 8z^3 + 3z^2 - 14z}{2z - 3}\)
- Answer
-
\(4z^5 + 4z^4 + 2z^3 + 7z^2 + 12z + 11 + \dfrac{33}{2z - 3}\)
\(\dfrac{9 a^{7}+15 a^{6}+4 a^{5}-3 a^{4}-a^{3}+12 a^{2}+a-5}{3 a+1}\)
\((2x^5 + 5x^4 -1) \div (2x + 5)\)
- Answer
-
\(x^4 - \dfrac{1}{2x + 5}\)
\((6a^4 - 2a^3 - 3a^2 + a + 4) \div (3a - 1)\)
Exercises For Review
Find the product. \(\dfrac{x^2 + 2x - 8}{x^2 - 9} \cdot \dfrac{2x + 6}{4x - 8}\)
- Answer
-
\(\dfrac{x + 4}{2(x-3)}\)
Find the sum. \(\dfrac{x-7}{x + 5} + \dfrac{x + 4}{x - 2}\)
Solve the equation \(\dfrac{1}{x + 3} + \dfrac{1}{x - 3} = \dfrac{1}{x^2 - 9}\)
- Answer
-
\(x = \dfrac{1}{2}\)
When the same number is subtracted from both the numerator and denominator of \(dfrac{3}{10}\), the result is \(\dfrac{1}{8}\). What is teh number that is subtracted?
Simplify \(\dfrac{\frac{1}{x+5}}{\frac{4}{x^{2}-25}}\)
- Answer
-
\(\dfrac{x-5}{4}\)