10.2: Solving Quadratic Equations
- Page ID
- 49402
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Standard Form of A Quadratic Equation
In Chapter 5 we studied linear equations in one and two variables and methods for solving them. We observed that a linear equation in one variable was any equation that could be written in the form \(ax + b = 0, a\not = 0\), and a linear equation in two variables was any equation that could be written in the form \(ax + by = c\), where \(a\) and \(b\) are not both \(0\). We now wish to study quadratic equations in one variable.
A quadratic equation is an equation of the form \(ax^2 + bx + c = 0, a \not = 0\).
The standard form of the quadratic equation is \(ax^2 + bx + c = 0, a \not = 0\).
For a quadratic equation in standard form \(ax^2 + bx + c = 0\),
\(a\) is the coefficient of \(x^2\).
\(b\) is the coefficient of \(x\).
\(c\) is the constant term.
Sample Set A
The following are quadratic equations.
\(3x^2 + 2x - 1 = 0\). \(a = 3, b = 2, c = -1\)
\(5x^2 + 8x = 0\). \(a = 5, b = 8, c = 0\)
Notice that this equation could be written \(5x^2 + 8x + 0 = 0\). Now it is clear that \(c = 0\).
\(x^2 + 7 = 0\). \(a = 1, b = 0, c = 7\).
Notice that this equation could be written \(x^2 + 0x + 7 = 0\). Now it is clear that \(b = 0\)
The following are not quadratic equations.
\(3x + 2 = 0\). \(a = 0\). This equation is linear.
\(8x^2 + \dfrac{3}{x} - 5 = 0\)
The expression on the left side of the equal sign has a variable in the denominator and, therefore is not a quadratic.
Practice Set A
Which of the following equations are quadratic equations? Answer “yes” or “no” to each equation.
\(6x^2 - 4x + 9 = 0\)
- Answer
-
yes
\(5x+8=0\)
- Answer
-
no
\(4x^3 - 5x^2 + x + 6 = 8\)
- Answer
-
no
\(4x^2 - 2x + 4 = 1\)
- Answer
-
yes
\(\dfrac{2}{x} - 5x^2 = 6x + 4\)
- Answer
-
no
\(9x^2 - 2x + 6 = 4x^2 + 8\)
- Answer
-
yes
Zero-Factor Property
Our goal is to solve quadratic equations. The method for solving quadratic equations is based on the zero-factor property of real numbers. We were introduced to the zero-factor property in Section 8.2. We state it again.
If two numbers \(a\) and \(b\) are multiplied together adn the resulting product is \(0\), then at least one of the numbers must be \(0\). Algebraically, if \(a \cdot b = 0\), then \(a = 0\) or both \(a = 0\) and \(b = 0\).
Sample Set B
Use the zero-factor property to solve each equation.
If \(9x = 0\), then \(x\) must be \(0\).
If \(-2x^2 = 0\), then \(x^2 = 0, x = 0\)
If \(5\) then \(x-1\) must be \(0\), since \(5\) is not zero.
\(\begin{array}{flushleft}
x - 1 &= 0\\
x &= 1
\end{array}\)
If \(x(x+6) = 0\), then
\(\begin{array}{flushleft}
x &= 0 & \text{ or } & x+6&=0\\
x&=0, -6 && x &= -6
\end{array}\)
If \((x+2)(x+3) = 0\), then
\(\begin{array}{flushleft}
x + 2 &= 0 & \text{ or } & x + 3 &= 0\\
x &= -2 && x &= -3\\
x &= -2, -3
\end{array}\)
If \((x+10)(4x - 5) = 0\), then
\(\begin{array}{flushleft}
x + 10 &= 0 & \text{ or } & 4x - 5 &= 0\\
x &= -10 && 4x &= 5\\
x &= -10, \dfrac{5}{4} && x &= \dfrac{5}{4}
\end{array}\)
Practice Set B
Use the zero-factor property to solve each equation.
\(6(a−4)=0\)
- Answer
-
\(a=4\)
\((y+6)(y−7)=0\)
- Answer
-
\(y=−6, 7\)
\((x+5)(3x−4)=0\)
- Answer
-
\(x = -5, \dfrac{4}{3}\)
Exercises
For the following problems, write the values of \(a\), \(b\), and \(c\) in quadratic equations.
\(3x^2 + 4x - 7 = 0\)
- Answer
-
\(3,4,−7\)
\(7x^2 + 2x + 8 = 0\)
\(2y^2 - 5y + 5 = 0\)
- Answer
-
\(2,−5,5\)
\(7a^2 + a - 8 = 0\).
\(-3a^2 + 4a - 1 = 0\)
- Answer
-
\(−3,4,−1\)
\(7b^2 + 3b + 0\)
\(2x^2 + 5x + 0\)
- Answer
-
\(2, 5, 0\)
\(4y^2 + 9 = 0\)
\(8a^2 - 2a = 0\)
- Answer
-
\(8,−2,0\)
\(6x^2 = 0\)
\(4y^2 = 0\)
- Answer
-
\(4, 0, 0\)
\(5x^2 - 3x + 9 = 4x^2\)
\(7x^2 + 2x + 1 = 6x^2 + x - 9\)
- Answer
-
\(1, 1, 10\)
\(-3x^2 + 4x - 1 = -4x^2 - 4x + 12\)
\(5x - 7 = -3x^2\)
- Answer
-
\(3,5,−7\)
\(3x - 7 = -2x^2 + 5x\)
\(0 = x^2 + 6x - 1\)
- Answer
-
\(1,6,−1\)
\(9 = x^2\)
\(x^2 = 9\)
- Answer
-
\(1,0,−9\)
\(0 = -x ^2\)
For the following problems, use the zero-factor property to solve the equations.
\(4x = 0\)
- Answer
-
\(x=0\)
\(16y=0\)
\(9a=0\)
- Answer
-
\(a=0\)
\(4m=0\)
\(3(k+7)=0\)
- Answer
-
\(k=−7\)
\(8(y−6)=0\)
\(−5(x+4)=0\)
- Answer
-
\(x=−4\)
\(−6(n+15)=0\)
\(y(y−1)=0\)
- Answer
-
\(y=0,1\)
\(a(a−6)=0\)
\(n(n+4)=0\)
- Answer
-
\(n=0,−4\)
\(x(x+8)=0\)
\(9(a−4)=0\)
- Answer
-
\(a=4\)
\(−2(m+11)=0\)
\(x(x+7) = 0\)
- Answer
-
\(x=−7 \text{ or } x=0\)
\(n(n−10)=0\)
\((y−4)(y−8)=0\)
- Answer
-
\(y=4 \text{ or } y=8\)
\((k−1)(k−6)=0\)
\((x+5)(x+4)=0\)
- Answer
-
\(x=−4 \text{ or } x=−5\)
\((y+6)(2y+1)=0\)
\((x−3)(5x−6)=0\)
- Answer
-
\(x = \dfrac{6}{5} \text{ or } x = 3\)
\((5a+1)(2a−3)=0\)
\((6m+5)(11m−6)=0\)
- Answer
-
\(m = -\dfrac{5}{6} \text{ or } m = \dfrac{6}{11}\)
\((2m−1)(3m+8)=0\)
\((4x+5)(2x−7)=0\)
- Answer
-
\(x = \dfrac{-5}{4}, \dfrac{7}{2}\)
\((3y + 1)(2y + 1) = 0\)
\((7a + 6)(7a - 6) = 0\)
- Answer
-
\(a = \dfrac{-6}{7}, \dfrac{6}{7}\)
\((8x+11)(2x−7)=0\)
\((5x−14)(3x+10)=0\)
- Answer
-
\(x = \dfrac{14}{5}, \dfrac{-10}{3}\)
\((3x−1)(3x−1)=0\)
\((2y+5)(2y+5)=0\)
- Answer
-
\(y = \dfrac{-5}{2}\)
\((7a - 2)^2 = 0\)
\((5m - 6)^2 = 0\)
- Answer
-
\(m = \dfrac{6}{5}\)
Exercises For Review
Factor \(12ax - 3x + 8a - 2\) by grouping.
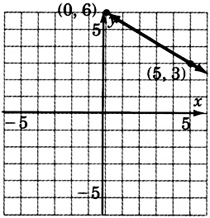
Construct the graph of \(6x + 10y - 60 = 0\)
- Answer
-
Find the difference: \(\dfrac{1}{x^2 + 2x + 1} - \dfrac{1}{x^2 - 1}\).
Simplify \(\sqrt{7}(\sqrt{2} + 2)\)
- Answer
-
\(\sqrt{14} + 2\sqrt{7}\)
Solve the radical equation \(\sqrt{3x + 10} = x + 4\)