6.7: Applications Involving Quadratic Equations
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Set up and solve applications involving relationships between real numbers.
- Set up and solve applications involving geometric relationships involving area and the Pythagorean theorem.
- Set up and solve applications involving the height of projectiles.
Number Problems
The algebraic setups of the word problems that we have previously encountered led to linear equations. When we translate the applications to algebraic setups in this section, the setups lead to quadratic equations. Just as before, we want to avoid relying on the “guess and check” method for solving applications. Using algebra to solve problems simplifies the process and is more reliable.
One integer is 4 less than twice another integer, and their product is 96. Set up an algebraic equation and solve it to find the two integers.
Solution:
First, identify the variables. Avoid two variables by using the relationship between the two unknowns.
.png?revision=1)
The key phrase, “their product is 96,” indicates that we should multiply and set the product equal to 96.
n⋅(2n−4)=96
Once we have the problem translated to a mathematical equation, we then solve. In this case, we can solve by factoring. The first step is to write the equation in standard form:
n⋅(2n−4)=96Distributen.2n2−4n=96Subtract96frombothsides.2n2−4n−96=0
Next, factor completely and set each variable factor equal to zero.
2n2−4n−96=0FactorouttheGCF,2.2(n2−2n−48)=0Factortheresultingtrinomial.2(n+6)(n−8)=0Seteachvariablefactorequaltozero.
n+6=0orn−8=0n=−6n=8
The problem calls for two integers whose product is +96. The product of two positive numbers is positive and the product of two negative numbers is positive. Hence we can have two sets of solutions. Use 2n−4 to determine the other integers.
n=−6n=82n−4=2(−6)−42n−4=2(8)−4=−12−4=16−4=−16=12
Answer:
Two sets of integers solve this problem: {8,12} and {−6,−16}. Notice that (8)(12)=96 and (−6)(−16)=96; our solutions check out.
With quadratic equations, we often obtain two solutions for the identified unknown. Although it may be the case that both are solutions to the equation, they may not be solutions to the problem. If a solution does not solve the original application, then we disregard it.
Recall that consecutive odd and even integers both are separated by two units.
.png?revision=1)
The product of two consecutive positive odd integers is 99. Find the integers.
Solution:
Let n represent the first positive odd integer.
Let n+2 represent the next positive odd integer.
The key phase, “product…is 99,” indicates that we should multiply and set the product equal to 99.
n⋅(n+2)=99
Rewrite the quadratic equation in standard form and solve by factoring.
n2+2n=99n2+2n−99=0(n−9)(n+11)=0
n−9=0orn+11=0n=9n=−11
Because the problem asks for positive integers, n=9 is the only solution. Back substitute to determine the next odd integer.
n+2=9+2=11
Answer:
The consecutive positive odd integers are 9 and 11.
Given two consecutive positive odd integers, the product of the larger and twice the smaller is equal to 70. Find the integers.
Solution:
Let n represent the smaller positive odd integer.
Let n+2 represent the next positive odd integer.
The key phrase “twice the smaller” can be translated to 2n. The phrase “product…is 70” indicates that we should multiply this by the larger odd integer and set the product equal to 70.
(n+2)⋅2n=70
Solve by factoring.
(n+2)⋅2n=70Distribute.2n2+4n=70Subtract70frombothsides.2n2+4n−70=0FactorouttheGCF,2.2(n2+2n−35)=0Factortheresultingtrinomial.2(n−5)(n+7)=0Seteachvariablefactorequaltozero.
n−5=0orn+7=0n=5n=−7
Because the problem asks for positive integers, n=5 is the only solution.
Back substitute into n+2 to determine the next odd integer.
n+2=5+2=7
Answer:
The positive odd integers are 5 and 7.
The product of two consecutive positive even integers is 168. Find the integers.
- Answer
-
The positive even integers are 12 and 14.
Geometry Problems
When working with geometry problems, it is helpful to draw a picture. Below are some area formulas that you are expected to know. (Recall that π≈3.14.)
| Area of a rectangle: | A=l⋅w |
| Area of a square: | A=s2 |
| Area of a triangle: | A=12bh |
| Area of a circle: | A=πr2 |
The floor of a rectangular room has a length that is 4 feet more than twice its width. If the total area of the floor is 240 square feet, then find the dimensions of the floor.
Solution:
.png?revision=1)
Use the formula A=l⋅w and the fact that the area is 240 square feet to set up an algebraic equation.
A=l⋅w240=(2w+4)⋅w
Solve by factoring.
w−10=0orw+12=0w=10w=−12
At this point we have two possibilities for the width of the rectangle. However, since a negative width is not defined, choose the positive solution, w=10. Back substitute to find the length.
2w+4=2(10)+4=20+4=24
Answer:
The width is 10 feet and the length is 24 feet.
It is important to include the correct units in the final presentation of the answer. In the previous example, it would not make much sense to say the width is 10. Make sure to indicate that the width is 10 feet.
The height of a triangle is 3 inches less than twice the length of its base. If the total area of the triangle is 7 square inches, then find the lengths of the base and height.
Solution:
.png?revision=1)
Use the formula A=12bh and the fact that the area is 7 square inches to set up an algebraic equation.
A=12b⋅h7=12b(2b−3)
To avoid fractional coefficients, multiply both sides by 2 and then rewrite the quadratic equation in standard form.
Factor and then set each factor equal to zero.
2b−7=0orb+2=02b=7b=−2b=72
In this case, disregard the negative answer; the length of the base is 72 inches long. Use 2b−3 to determine the height of the triangle.
Answer:
The base measures 72=312 inches and the height is 4 inches.
The base of a triangle is 5 units less than twice the height. If the area is 75 square units, then what is the length of the base and height?
- Answer
-
The height is 10 units and the base is 15 units.
Recall that a right triangle is a triangle where one of the angles measures 90°. The side opposite of the right angle is the longest side of the triangle and is called the hypotenuse. The Pythagorean theorem gives us a relationship between the legs and hypotenuse of any right triangle, where a and b are the lengths of the legs and c is the length of the hypotenuse:
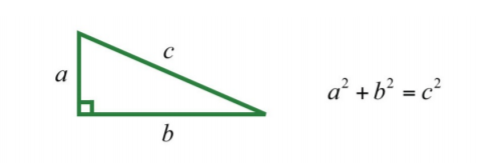.png?revision=1)
Given certain relationships, we use this theorem when determining the lengths of sides of right triangles.
The hypotenuse of a right triangle is 10 inches. If the short leg is 2 inches less than the long leg, then find the lengths of the legs.
Solution:
.png?revision=1)
Given that the hypotenuse measures 10 inches, substitute its value into the Pythagorean theorem and obtain a quadratic equation in terms of x.
a2+b2=c2(x−2)2+x2=102
Multiply and rewrite the equation in standard form.
(x−2)2+x2=102x2−4x+4+x2=1002x2−4x−96=0
Once it is in standard form, factor and set each variable factor equal to zero.
2x2−4x−96=02(x2−2x−48)=02(x+6)(x−8)=0
x+6=0orx−8=0x=−6x=8
Because lengths cannot be negative, disregard the negative answer. In this case, the long leg measures 8 inches. Use x−2 to determine the length of the short leg.
x−2=8−2=6
Answer:
The short leg measures 6 inches and the long leg measures 8 inches.
One leg of a right triangle measures 3 centimeters. The hypotenuse of the right triangle measures 3 centimeters less than twice the length of the unknown leg. Find the measure of all the sides of the triangle.
Solution:
.png?revision=1)
To set up an algebraic equation, we use the Pythagorean theorem.
a2+b2=c232+x2=(2x−3)2
Solve by factoring.
32+x2=(2x−3)29+x2=4x2−12x+90=3x2−12x0=3x(x−4)
3x=0orx−4=0x=0x=4
Disregard 0. The length of the unknown leg is 4 centimeters. Use 2x−3 to determine the length of the hypotenuse.
Answer:
The sides of the triangle measure 3 centimeters, 4 centimeters, and 5 centimeters.
The hypotenuse of a right triangle measures 13 units. If one leg is 2 units more than twice that of the other, then find the length of each leg.
- Answer
-
The two legs measure 5 units and 12 units.
Projectile Problems
The height of an object launched upward, ignoring the effects of air resistance, can be modeled with the following formula:
height=−12gt2+v0t+s0
Using function notation, which is more appropriate, we have
h(t)=−12gt2+v0t+s0
With this formula, the height can be calculated at any given time t after the object is launched. The coefficients represent the following:
| −12g | The letter g represents the acceleration due to gravity. |
| v0 | “v-naught” represents the initial velocity of the object. |
| s0 | “s-naught” represents the initial height from which the object is launched. |
We consider only problems where the acceleration due to gravity can be expressed as g=32 ft/sec2. Therefore, in this section time will be measured in seconds and the height in feet. Certainly though, the formula is valid using units other than these.
The height of a projectile launched upward at a speed of 32 feet/second from a height of 128 feet is given by the function h(t)=−16t2+32t+128. How long does it take to hit the ground?
Solution:
An inefficient method for finding the time to hit the ground is to simply start guessing at times and evaluating. To do this, construct a chart.
.png?revision=1)
Use the table to sketch the height of the projectile over time.
.png?revision=1)
We see that at 4 seconds, the projectile hits the ground. Note that when this occurs, the height is equal to 0. Now we need to solve this problem algebraically. To find the solution algebraically, use the fact that the height is 0 when the object hits the ground. We need to find the time, t, when h(t)=0.
h(t)=−16t2+32t+128↓0=−16t2+32t+128
Solve the equation by factoring
0=−16t2+32t+1280=−16(t2−2t−8)0=−16(t−4)(t+2)
Now set each variable factor to zero.
t−4=0ort+2=0t=4t=−2
As expected, the projectile hits the ground at t=4 seconds. Disregard −2 as a solution because negative time is not defined.
Answer:
The projectile hits the ground 4 seconds after it is launched.
The height of a certain book dropped from the top of a 144 foot building is given by h(t)=−16t2+144. How long does it take to hit the ground?
Solution:
Find the time t when the height h(t)=0.
0=−16t2+1440=−16(t2−9)0=−16(t+3)(t−3)
t+3=0ort−3=0t=−3t=3
Answer:
The book takes 3 seconds to hit the ground when dropped from the top of a 144-foot building.
The height of a projectile, shot straight up into the air from the ground, is given by h(t)=−16t2+80t. How long does it take to come back down to the ground?
- Answer
-
It will take 5 seconds to come back down to the ground.
Key Takeaways
- It is best to translate a word problem to a mathematical setup and then solve using algebra. Avoid using the “guess and check” method of solving applications in this section.
- When solving applications, check that your solutions make sense in the context of the question. For example, if you wish to find the length of the base of a triangle, then you would disregard any negative solutions.
- It is important to identify each variable and state in a sentence what each variable represents. It is often helpful to draw a picture.
Set up an algebraic equation and then solve.
- One integer is five times another. If the product of the two integers is 80, then find the integers.
- One integer is four times another. If the product of the two integers is 36, then find the integers.
- An integer is one more than four times another. If the product of the two integers is 39, then find the integers.
- An integer is 3 more than another. If the product of the two integers is 130, then find the integers.
- An integer is 2 less than twice another. If the product of the two integers is 220, then find the integers.
- An integer is 3 more than twice another. If the product of the two integers is 90, then find the integers.
- One integer is 2 units more than another. If the product of the two integers is equal to five times the larger, then find the two integers.
- A positive integer is 1 less than twice another. If the product of the two integers is equal to fifteen times the smaller, then find the two integers.
- A positive integer is 3 more than twice a smaller positive integer. If the product of the two integers is equal to six times the larger, then find the integers.
- One positive integer is 3 more than another. If the product of the two integers is equal to twelve times the smaller, then find the integers.
- An integer is 3 more than another. If the product of the two integers is equal to 2 more than four times their sum, then find the integers.
- An integer is 5 more than another. If the product of the two integers is equal to 2 more than twice their sum, then find the integers.
- The product of two consecutive positive even integers is 120. Find the integers.
- The product of two consecutive positive odd integers is 99. Find the integers.
- The product of two consecutive positive integers is 110. Find the integers.
- The product of two consecutive positive integers is 42. Find the integers.
- The product of two consecutive positive odd integers is equal to 1 less than seven times the sum of the integers. Find the integers.
- The product of two consecutive positive even integers is equal to 22 more than eleven times the sum of the integers. Find the integers.
- The sum of the squares of two consecutive positive odd integers is 74. Find the integers.
- The sum of the squares of two consecutive positive even integers is 100. Find the integers.
- The sum of the squares of two consecutive positive integers is 265. Find the integers.
- The sum of the squares of two consecutive positive integers is 181. Find the integers.
- For two consecutive positive odd integers, the product of twice the smaller and the larger is 126. Find the integers.
- For two consecutive positive even integers, the product of the smaller and twice the larger is 160. Find the integers.
- Answer
-
1. {4,20} or {−4,−20}
3. 3,13
5. {11,20} or {−22,−10}
7. {5,7} or {−2,0}
9. 6,15
11. {7,10} or {−2,1}
13. 10,12
15. 10,11
17. 13,15
19. 5,7
21. 11,12
23. 7,9
Set up an algebraic equation and then solve.
- The width of a rectangle is 7 feet less than its length. If the area of the rectangle is 170 square feet, then find the length and width.
- The length of a rectangle is 2 feet more than its width. If the area of the rectangle is 48 square feet, then find the length and width.
- The width of a rectangle is 3 units less than the length. If the area is 70 square units, then find the dimensions of the rectangle.
- The width of a rectangle measures one half of the length. If the area is 72 square feet, then find the dimensions of the rectangle.
- The length of a rectangle is twice that of its width. If the area of the rectangle is 72 square inches, then find the length and width.
- The length of a rectangle is three times that of its width. If the area of the rectangle is 75 square centimeters, then find the length and width.
- The length of a rectangle is 2 inches more than its width. The area of the rectangle is equal to 12 inches more than three times the perimeter. Find the length and width of the rectangle.
- The length of a rectangle is 3 meters more than twice the width. The area of the rectangle is equal to 10 meters less than three times the perimeter. Find the length and width of the rectangle.
- A uniform border is to be placed around an 8-inch-by-10-inch picture. If the total area including the border must be 224 square inches, then how wide should the border be?
.png?revision=1)
10. A 2-foot brick border is constructed around a square cement slab. If the total area, including the border, is 121 square feet, then what are the dimensions of the slab?
11. The area of a picture frame including a 2-inch wide border is 99 square inches. If the width of the inner area is 2 inches more than its length, then find the dimensions of the inner area.
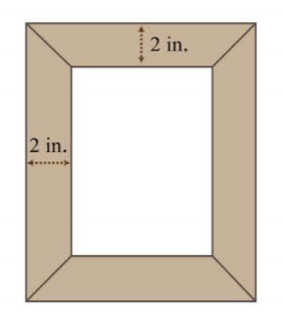.png?revision=1)
12. A box can be made by cutting out the corners and folding up the edges of a square sheet of cardboard. A template for a cardboard box with a height of 2 inches is given. What is the length of each side of the cardboard sheet if the volume of the box is to be 50 cubic inches?
.png?revision=1)
13. The height of a triangle is 3 inches more than the length of its base. If the area of the triangle is 44 square inches, then find the length of its base and height.
14. The height of a triangle is 4 units less than the length of the base. If the area of the triangle is 48 square units, then find the length of its base and height.
15. The base of a triangle is twice that of its height. If the area is 36 square centimeters, then find the length of its base and height.
16. The height of a triangle is three times the length of its base. If the area is 7312 square feet, then find the length of the base and height.
17. The height of a triangle is 1 unit more than the length of its base. If the area is 5 units more than four times the height, then find the length of the base and height of the triangle.
18. The base of a triangle is 4 times that of its height. If the area is 3 units more than five times the height, then find the length of the base and height of the triangle.
19. The diagonal of a rectangle measures 5 inches. If the length is 1 inch more than its width, then find the dimensions of the rectangle.
20. The diagonal of a rectangle measures 10 inches. If the width is 2 inches less than the length, then find the area of the rectangle.
21. If the sides of a right triangle are consecutive even integers, then what are their measures?
22. The hypotenuse of a right triangle is 13 units. If the length of one leg is 2 more than twice the other, then what are their lengths?
23. The shortest leg of a right triangle measures 9 centimeters and the hypotenuse measures 3 centimeters more than the longer leg. Find the length of the hypotenuse.
24. The long leg of a right triangle measures 24 centimeters and the hypotenuse measures 4 centimeters more three times the short leg. Find the length of the hypotenuse.
- Answer
-
1. Length: 17 feet; width: 10 feet
3. Length: 10 units; width: 7 units
5. Length: 12 inches; width: 6 inches
7. Length: 14 inches; width: 12 inches
9. 3 inches
11. 5 inches by 7 inches
13. Base: 8 inches; height: 11 inches
15. Base: 12 centimeters; height: 6 centimeters
17. Base: 9 units; height: 10 units
19. 3 inches by 4 inches
21. 6 units, 8 units, and 10 units
23. 15 centimeters
Set up an algebraic equation and then solve.
- The height of a projectile launched upward at a speed of 32 feet/second from a height of 48 feet is given by the function \(h(t)=−16t^{2}+32t+48. How long will it take the projectile to hit the ground?
- The height of a projectile launched upward at a speed of 16 feet/second from a height of 192 feet is given by the function h(t)=−16t2+16t+192. How long will it take to hit the ground?
- An object launched upward at a speed of 64 feet/second from a height of 80 feet. How long will it take the projectile to hit the ground?
- An object launched upward at a speed of 128 feet/second from a height of 144 feet. How long will it take the projectile to hit the ground?
- The height of an object dropped from the top of a 64-foot building is given by h(t)=−16t2+64. How long will it take the object to hit the ground?
- The height of an object dropped from an airplane at 1,600 feet is given by h(t)=−16t2+1,600. How long will it take the object to hit the ground?
- An object is dropped from a ladder at a height of 16 feet. How long will it take to hit the ground?
- An object is dropped from a 144-foot building. How long will it take to hit the ground?
- The height of a projectile, shot straight up into the air from the ground at 128 feet/second, is given by h(t)=−16t2+128t. How long does it take to come back down to the ground?
- A baseball, tossed up into the air from the ground at 32 feet/second, is given by h(t)=−16t2+32t. How long does it take to come back down to the ground?
- How long will it take a baseball thrown into the air at 48 feet/second to come back down to the ground?
- A football is kicked up into the air at 80 feet/second. Calculate how long will it hang in the air.
- Answer
-
1. 3 seconds
3. 5 seconds
5. 2 seconds
7. 1 second
9. 8 seconds
11. 3 seconds
- Research and discuss the life of Pythagoras.
- If the sides of a square are doubled, then by what factor is the area increased? Why?
- Design your own geometry problem involving the area of a rectangle or triangle. Post the question and a complete solution on the discussion board.
- Write down your strategy for setting up and solving word problems. Share your strategy on the discussion board.
- Answer
-
1. Answers may vary
3. Answers may vary


