1.9E: Exercises

Last updated
Save as PDF

Page ID: 30098

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Simplify Expressions with Square Roots

In the following exercises, simplify.

1. $\sqrt{36}$

Answer: $\sqrt{36} = 6$

2. $\sqrt{4}$

3. $\sqrt{64}$

Answer: $\sqrt{64} = 8$

4. $\sqrt{169}$

5. $\sqrt{9}$

Answer: $\sqrt{9} = 3$

6. $\sqrt{16}$

7. $\sqrt{100}$

Answer: $\sqrt{100} = 10$

8. $\sqrt{144}$

9. $\sqrt{−4}$

Answer: $\sqrt{-4}$ is not a real number.

10. $\sqrt{−100}$

11. $\sqrt{−1}$

Answer: $\sqrt{-1}$ is not a real number.

12. $\sqrt{−121}$

Identify Integers, Rational Numbers, Irrational Numbers, and Real Numbers

In the following exercises, write each rational number as the ratio of two integers.

13. ⓐ 5 ⓑ 3.19

Answer: a. $5 = \frac{5}{1}$ b. $3.19 = \frac{319}{100}$

14. ⓐ 8 ⓑ 1.61

15. ⓐ −12 ⓑ 9.279

Answer: a. $-12 = \frac{-12}{1}$ b. $9.279 = \frac{9279}{1000}$

16. ⓐ −16 ⓑ 4.399

In the following exercises, list the ⓐ rational numbers, ⓑ irrational numbers

17. {0.75, $0.22\overline{3}$, 1.39174}

Answer: All of these numbers are rational.

18. {0.36, 0.94729…, $2.52\overline{8}$}

19. {$0.4\overline{5}$, 1.919293…, 3.59}

Answer: a. $0.4\overline{5}$ and 3.59 are rational numbers. b. 1.919293… is irrational, since it does not terminate or repeat.

20. {$0.1\overline{3}$, 0.42982…, 1.875}

In the following exercises, identify whether each number is rational or irrational.

21. ⓐ $\sqrt{25}$ ⓑ $\sqrt{30}$

Answer: a. $\sqrt{25} = 5$ is rational. b. $\sqrt{30}$ is irrational.

22. ⓐ $ \sqrt{44} $ ⓑ $ \sqrt{49} $

23. ⓐ $ \sqrt{164} $ ⓑ $ \sqrt{169} $

Answer: a. $\sqrt{164}$ is irrational. b. $\sqrt{169} = 13$ is rational.

24. ⓐ $ \sqrt{225} $ ⓑ $ \sqrt{216} $

In the following exercises, identify whether each number is a real number or not a real number.

25. ⓐ $ -\sqrt{81} $ ⓑ $ \sqrt{-121} $

Answer: a. $-\sqrt{81} = -9$ is a real number. b. $\sqrt{-121}$ is not a real number.

26. ⓐ $ -\sqrt{64} $ ⓑ $ \sqrt{-9} $

27. ⓐ $ \sqrt{-36} $ ⓑ $ -\sqrt{144} $

Answer: a. $\sqrt{-36}$ is not a real number. b. $-\sqrt{144} = -12$ is a real number.

28. ⓐ $ \sqrt{-49} $ ⓑ $ -\sqrt{144} $

In the following exercises, for each set of numbers, list the ⓐ whole numbers, ⓑ integers, ⓒ rational numbers, ⓓ irrational numbers, ⓔ real numbers.

29. {−8, 0, 1.95286…, $\tfrac{12}{5}$, $\sqrt{36}$, 9}

Answer: a. whole numbers: 0,  $\sqrt{36} = 6$, 9
b. integers: -8, 0,  $\sqrt{36} = 6$, 9
c. rational numbers: -8, 0,  $\sqrt{36} = 6$, 9, $\tfrac{12}{5}$
d. irrational numbers: 1.95286…
e. real numbers: All of these numbers are real numbers.

30. {−9, $−3\tfrac{4}{9}$, $-\sqrt{9}$, $0.40\overline{9}$, 116, 7}

31. {$-\sqrt{100}$, −7, $−\tfrac{8}{3}$, −1, 0.77, $3\tfrac{1}{4}$}

Answer: a. whole numbers: None of these numbers are whole numbers.
b. integers: $-\sqrt{100}=-10$, −7, -1
c. rational numbers: All of these numbers are rational.
d. irrational numbers: None of these numbers is irrational.
e. real numbers: All of these numbers are real numbers.

32. {−6, $−\tfrac{5}{2}$, 0, $0.\overline{714285}$, $2\tfrac{1}{5}$, $\sqrt{14}$}

Locate Fractions on the Number Line

In the following exercises, locate the numbers on a number line.

33. $\tfrac{3}{4}, \tfrac{8}{5}, \tfrac{10}{3}$

Answer: $Number line showing these numbers$

34. $\tfrac{1}{4}, \tfrac{9}{5}, \tfrac{11}{3}$

35. $\frac{3}{10}, \frac{7}{2}, \frac{11}{6}, 4$

Answer: $Number line showing these numbers$

36. $\frac{7}{10}, \frac{5}{2}, \frac{13}{8}, 3$

37. $\frac{2}{5}, −\frac{2}{5}$

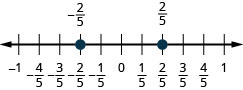
Answer: $Number line showing these numbers$

38. $\frac{3}{4},−\frac{3}{4}$

39. $\frac{3}{4},−\frac{3}{4}, 1\tfrac{2}{3}, −1\tfrac{2}{3}, \frac{5}{2}, −\frac{5}{2}$

Answer: $Number line showing these numbers$

40. $\frac{1}{5}, −\frac{2}{5}, 1\tfrac{3}{4}, −1\tfrac{3}{4}, \frac{8}{3}, −\frac{8}{3}$

In the following exercises, order each of the pairs of numbers, using < or >.

41. −1 ___ $−\frac{1}{4}$

Answer: $−1 < −\frac{1}{4}$

42. −1 ___ $−\frac{1}{3}$

43. $−2\tfrac{1}{2}$ ___ −3

Answer: $−2\tfrac{1}{2} > −3$

44. $−1\tfrac{3}{4}$ ___ −2

45. $−\frac{5}{12}$ ___ $−\frac{7}{12}$

Answer: $−\frac{5}{12} > −\frac{7}{12}$

46. $−\frac{9}{10}$ ___ $−\frac{3}{10}$

47. −3 ___ $−\frac{13}{5}$

Answer: $−3 < −\frac{13}{5}$

48. −4 ___ $−\frac{23}{6}$

Locating Decimals on the Number Line In the following exercises, locate the number on the number line.

49. 0.8

Answer: $Number line showing this number$

50. −0.9

51. −1.6

Answer: $Number line showing this number$

52. 3.1

In the following exercises, order each pair of numbers, using < or >.

53. 0.37 ___ 0.63

Answer: 0.37 < 0.63

54. 0.86 ___ 0.69

55. 0.91 ___ 0.901

Answer: 0.91 > 0.901

56. 0.415 ___ 0.41

57. −0.5 ___ −0.3

Answer: −0.5 < −0.3

58. −0.1 ___ −0.4

59. −0.62 ___ −0.619

Answer: −0.62 < −0.619

60. −7.31 ___ −7.3

Everyday Math

61. Field trip All the 5th graders at Lincoln Elementary School will go on a field trip to the science museum. Counting all the children, teachers, and chaperones, there will be 147 people. Each bus holds 44 people.

ⓐ How many busses will be needed?
ⓑ Why must the answer be a whole number?
ⓒ Why shouldn’t you round the answer the usual way, by choosing the whole number closest to the exact answer?

62. Child care Serena wants to open a licensed child care center. Her state requires there be no more than 12 children for each teacher. She would like her child care center to serve 40 children.

ⓐ How many teachers will be needed?
ⓑ Why must the answer be a whole number?
ⓒ Why shouldn’t you round the answer the usual way, by choosing the whole number closest to the exact answer?

Writing Exercises

63. In your own words, explain the difference between a rational number and an irrational number.

64. Explain how the sets of numbers (counting, whole, integer, rational, irrationals, reals) are related to each other.

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objective of this section.

$This is a table that has five rows and four columns. In the first row, which is a header row, the cells read from left to right “I can…,” “Confidently,” “With some help,” and “No-I don’t get it!” The first column below “I can…” reads “simplify expressions with square roots,” “identify integers, rational numbers, irrational numbers and real numbers,” locate fractions on the number line,” and “locate decimals on the number line.” The rest of the cells are blank$

ⓑ On a scale of 1−10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Search

Text Color

Text Size

Margin Size

Font Type