3.1E: Exercises
- Page ID
- 30113
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Practice Makes Perfect
Use the Approach Word Problems with a Positive Attitude
In the following exercises, prepare the lists described.
List five positive thoughts you can say to yourself that will help you approach word problems with a positive attitude. You may want to copy them on a sheet of paper and put it in the front of your notebook, where you can read them often.
- Answer
-
Answers will vary
List five negative thoughts that you have said to yourself in the past that will hinder your progress on word problems. You may want to write each one on a small piece of paper and rip it up to symbolically destroy the negative thoughts.
Use a Problem-Solving Strategy for Word Problems
In the following exercises, solve using the problem solving strategy for word problems. Remember to write a complete sentence to answer each question.
Two-thirds of the children in the fourth-grade class are girls. If there are 20 girls, what is the total number of children in the class?
- Answer
-
30
Three-fifths of the members of the school choir are women. If there are 24 women, what is the total number of choir members?
Zachary has 25 country music CDs, which is one-fifth of his CD collection. How many CDs does Zachary have?
- Answer
-
125
One-fourth of the candies in a bag of M&M’s are red. If there are 23 red candies, how many candies are in the bag?
There are 16 girls in a school club. The number of girls is four more than twice the number of boys. Find the number of boys.
- Answer
-
6
There are 18 Cub Scouts in Pack 645. The number of scouts is three more than five times the number of adult leaders. Find the number of adult leaders.
Huong is organizing paperback and hardback books for her club’s used book sale. The number of paperbacks is 12 less than three times the number of hardbacks. Huong had 162 paperbacks. How many hardback books were there?
- Answer
-
58
Jeff is lining up children’s and adult bicycles at the bike shop where he works. The number of children’s bicycles is nine less than three times the number of adult bicycles. There are 42 adult bicycles. How many children’s bicycles are there?
Philip pays $1,620 in rent every month. This amount is $120 more than twice what his brother Paul pays for rent. How much does Paul pay for rent?
- Answer
-
$750
Marc just bought an SUV for $54,000. This is $7,400 less than twice what his wife paid for her car last year. How much did his wife pay for her car?
Laurie has $46,000 invested in stocks and bonds. The amount invested in stocks is $8,000 less than four times the amount invested in bonds. How much does Laurie have invested in bonds?
- Answer
-
$13,500
Erica earned a total of $50,450 last year from her two jobs. The amount she earned from her job at the store was $1,250 more than three times the amount she earned from her job at the college. How much did she earn from her job at the college?
Solve Number Problems
In the following exercises, solve each number word problem.
The sum of a number and eight is 12. Find the number.
- Answer
-
4
The sum of a number and nine is 17. Find the number.
The difference of a number and 12 is three. Find the number.
- Answer
-
15
The difference of a number and eight is four. Find the number.
The sum of three times a number and eight is 23. Find the number.
- Answer
-
5
The sum of twice a number and six is 14. Find the number.
The difference of twice a number and seven is 17. Find the number.
- Answer
-
12
The difference of four times a number and seven is 21. Find the number.
Three times the sum of a number and nine is 12. Find the number.
- Answer
-
-5
Six times the sum of a number and eight is 30. Find the number.
One number is six more than the other. Their sum is 42. Find the numbers.
- Answer
-
18, 24
One number is five more than the other. Their sum is 33. Find the numbers.
The sum of two numbers is 20. One number is four less than the other. Find the numbers.
- Answer
-
8, 12
The sum of two numbers is 27. One number is seven less than the other. Find the numbers.
The sum of two numbers is −45. One number is nine more than the other. Find the numbers.
- Answer
-
−18,−27
The sum of two numbers is −61. One number is 35 more than the other. Find the numbers.
The sum of two numbers is −316. One number is 94 less than the other. Find the numbers.
- Answer
-
−111,−205
The sum of two numbers is −284. One number is 62 less than the other. Find the numbers.
One number is 14 less than another. If their sum is increased by seven, the result is 85. Find the numbers.
- Answer
-
32, 46
One number is 11 less than another. If their sum is increased by eight, the result is 71. Find the numbers.
One number is five more than another. If their sum is increased by nine, the result is 60. Find the numbers.
- Answer
-
23, 28
One number is eight more than another. If their sum is increased by 17, the result is 95. Find the numbers.
One number is one more than twice another. Their sum is −5. Find the numbers.
- Answer
-
−2,−3
One number is six more than five times another. Their sum is six. Find the numbers.
The sum of two numbers is 14. One number is two less than three times the other. Find the numbers.
- Answer
-
4, 10
The sum of two numbers is zero. One number is nine less than twice the other. Find the numbers.
The sum of two consecutive integers is 77. Find the integers.
- Answer
-
38, 39
The sum of two consecutive integers is 89. Find the integers.
The sum of two consecutive integers is −23. Find the integers.
- Answer
-
−11,−12
The sum of two consecutive integers is −37. Find the integers.
The sum of three consecutive integers is 78. Find the integers.
- Answer
-
25, 26, 27
The sum of three consecutive integers is 60. Find the integers.
Find three consecutive integers whose sum is −36.
- Answer
-
−11,−12,−13
Find three consecutive integers whose sum is −3.
Find three consecutive even integers whose sum is 258.
- Answer
-
84, 86, 88
Find three consecutive even integers whose sum is 222.
Find three consecutive odd integers whose sum is 171.
- Answer
-
55, 57, 59
Find three consecutive odd integers whose sum is 291.
Find three consecutive even integers whose sum is −36.
- Answer
-
−10,−12,−14
Find three consecutive even integers whose sum is −84.
Find three consecutive odd integers whose sum is −213.
- Answer
-
−69,−71,−73
Find three consecutive odd integers whose sum is −267.
Everyday Math
Sale Price Patty paid $35 for a purse on sale for $10 off the original price. What was the original price of the purse?
- Answer
-
$45
Sale Price Travis bought a pair of boots on sale for $25 off the original price. He paid $60 for the boots. What was the original price of the boots?
Buying in Bulk Minh spent $6.25 on five sticker books to give his nephews. Find the cost of each sticker book.
- Answer
-
$1.25
Buying in Bulk Alicia bought a package of eight peaches for $3.20. Find the cost of each peach.
Price before Sales Tax Tom paid $1,166.40 for a new refrigerator, including $86.40 tax. What was the price of the refrigerator?
- Answer
-
$1080
Price before Sales Tax Kenji paid $2,279 for a new living room set, including $129 tax. What was the price of the living room set?
Writing Exercises
What has been your past experience solving word problems?
- Answer
-
answers will vary
When you start to solve a word problem, how do you decide what to let the variable represent?
What are consecutive odd integers? Name three consecutive odd integers between 50 and 60.
- Answer
-
Consecutive odd integers are odd numbers that immediately follow each other. An example of three consecutive odd integers between 50 and 60 would be 51, 53, and 55.
What are consecutive even integers? Name three consecutive even integers between −50 and −40.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
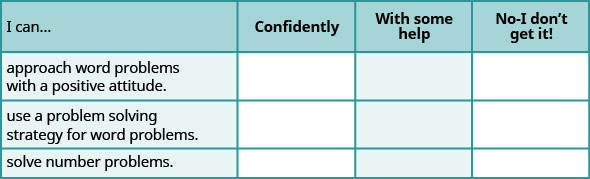
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved your goals in this section! Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific!
…with some help. This must be addressed quickly as topics you do not master become potholes in your road to success. Math is sequential—every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is critical and you must not ignore it. You need to get help immediately or you will quickly be overwhelmed. See your instructor as soon as possible to discuss your situation. Together you can come up with a plan to get you the help you need.


