3.1: Use a Problem-Solving Strategy
- Page ID
- 15136
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Approach word problems with a positive attitude
- Use a problem-solving strategy for word problems
- Solve number problems
Before you get started, take this readiness quiz.
- Translate “6 less than twice x” into an algebraic expression.
If you missed this problem, review Exercise 1.3.43. - Solve: \(\frac{2}{3}x=24\).
If you missed this problem, review Exercise 2.2.10. - Solve: \(3x+8=14\).
If you missed this problem, review Exercise 2.3.1.
Approach Word Problems with a Positive Attitude
“If you think you can… or think you can’t… you’re right.”—Henry Ford
The world is full of word problems! Will my income qualify me to rent that apartment? How much punch do I need to make for the party? What size diamond can I afford to buy my girlfriend? Should I fly or drive to my family reunion? How much money do I need to fill the car with gas? How much tip should I leave at a restaurant? How many socks should I pack for vacation? What size turkey do I need to buy for Thanksgiving dinner, and then what time do I need to put it in the oven? If my sister and I buy our mother a present, how much does each of us pay?
Now that we can solve equations, we are ready to apply our new skills to word problems. Do you know anyone who has had negative experiences in the past with word problems? Have you ever had thoughts like the student below (Figure \(\PageIndex{1}\))?

When we feel we have no control, and continue repeating negative thoughts, we set up barriers to success. We need to calm our fears and change our negative feelings.
Start with a fresh slate and begin to think positive thoughts. If we take control and believe we can be successful, we will be able to master word problems! Read the positive thoughts in Figure \(\PageIndex{2}\) and say them out loud.

Think of something, outside of school, that you can do now but couldn’t do 3 years ago. Is it driving a car? Snowboarding? Cooking a gourmet meal? Speaking a new language? Your past experiences with word problems happened when you were younger—now you’re older and ready to succeed!
Use a Problem-Solving Strategy for Word Problems
We have reviewed translating English phrases into algebraic expressions, using some basic mathematical vocabulary and symbols. We have also translated English sentences into algebraic equations and solved some word problems. The word problems applied math to everyday situations. We restated the situation in one sentence, assigned a variable, and then wrote an equation to solve the problem. This method works as long as the situation is familiar and the math is not too complicated.
Now, we’ll expand our strategy so we can use it to successfully solve any word problem. We’ll list the strategy here, and then we’ll use it to solve some problems. We summarize below an effective strategy for problem solving.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebraic equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Pilar bought a purse on sale for \($18\), which is one-half of the original price. What was the original price of the purse?
Solution
Step 1. Read the problem. Read the problem two or more times if necessary. Look up any unfamiliar words in a dictionary or on the internet.
In this problem, is it clear what is being discussed? Is every word familiar?Let p = the original price of the purse.
Step 2. Identify what you are looking for. Did you ever go into your bedroom to get something and then forget what you were looking for? It’s hard to find something if you are not sure what it is! Read the problem again and look for words that tell you what you are looking for!
In this problem, the words “what was the original price of the purse” tell us what we need to find.
Step 3. Name what we are looking for. Choose a variable to represent that quantity. We can use any letter for the variable, but choose one that makes it easy to remember what it represents.
Step 4. Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Translate the English sentence into an algebraic equation.
Reread the problem carefully to see how the given information is related. Often, there is one sentence that gives this information, or it may help to write one sentence with all the important information. Look for clue words to help translate the sentence into algebra. Translate the sentence into an equation.
| Restate the problem in one sentence with all the important information. | \(\color{cyan} \underbrace{\strut \color{black}\mathbf{18}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\color{black}\textbf{one-half the original price.}}\) |
| Translate into an equation. | \(18 \qquad = \qquad \qquad \qquad \frac{1}{2}\cdot p\) |
Step 5. Solve the equation using good algebraic techniques. Even if you know the solution right away, using good algebraic techniques here will better prepare you to solve problems that do not have obvious answers.
| Solve the equation. | \(18 = \frac{1}{2}p\) |
| Multiply both sides by 2. | \( {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p \) |
| Simplify. | \(36 = p\) |
Step 6. Check the answer in the problem to make sure it makes sense. We solved the equation and found that \(p=36\),which means “the original price” was \($36\).
Does $36 make sense in the problem? Yes, because 18 is one-half of 36, and the purse was on sale at half the original price.If this were a homework exercise, our work might look like this:
Pilar bought a purse on sale for \($18\), which is one-half the original price. What was the original price of the purse?
Step 7. Answer the question with a complete sentence. The problem asked “What was the original price of the purse?”
The answer to the question is: “The original price of the purse was $36.”| Let \(p =\) the original price. | |
| \(18\) is one-half the original price. | |
| \(18 = \frac{1}{2}p\) | |
| Multiply both sides by \(2\). | \( {\color{red}{2}}\cdot 18 = {\color{red}{2}}\cdot \frac{1}{2}p \) |
| Simplify. | \(36 = p\) |
| Check. Is \($36\) a reasonable price for a purse? | |
| Yes. | |
| Is \(18\) one half of \(36\)? | |
| \(18 \stackrel{?}{=} \frac{1}{2}\cdot 36\) | |
| \(18 = 18\checkmark\) | |
| The original price of the purse was \($36\). |
Joaquin bought a bookcase on sale for \($120\), which was two-thirds of the original price. What was the original price of the bookcase?
- Answer
-
\($180\)
Two-fifths of the songs in Mariel’s playlist are country. If there are \(16\) country songs, what is the total number of songs in the playlist?
Answer-
\(40\)
Let’s try this approach with another example.
Ginny and her classmates formed a study group. The number of girls in the study group was three more than twice the number of boys. There were \(11\) girls in the study group. How many boys were in the study group?
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | How many boys were in the study group? |
| Step 3. Name. Choose a variable to represent the number of boys. | Let \(n=\) the number of boys. |
| Step 4. Translate. Restate the problem in one sentence with all the important information. | \(\color{cyan} \underbrace{\color{black}\textbf{The number}\\ \color{black}\textbf{of girls}(11)} \quad \underbrace{\strut \text{ } \\ \color{black}\textbf{was}} \quad \underbrace{\color{black}\textbf{three more than}\\ \color{black}\textbf{twice the number of boys}}\) |
| Translate into an equation. | \(\qquad 11 \qquad \quad = \qquad \qquad \quad 2b + 3\) |
| Step 5. Solve the equation. | \(\quad 11 = 2b + 3 \) |
| Subtract 3 from each side. | \(\quad 11 \,{\color{red}{- \,3}} = 2b + 3 \,{\color{red}{- \,3}} \) |
| Simplify. | \(\quad 8 = 2b \) |
| Divide each side by 2. | \( \quad \dfrac{8}{\color{red}{2}}=\dfrac{2b}{\color{red}{2}} \) |
| Simplify. | \(\quad 4 = b\) |
| Step 6. Check. First, is our answer reasonable? Yes, having \(4\) boys in a study group seems OK. The problem says the number of girls was \(3\) more than twice the number of boys. If there are four boys, does that make eleven girls? Twice \(4\) boys is \(8\). Three more than \(8\) is \(11\). | |
| Step 7. Answer the question. | There were \(4\) boys in the study group. |
Guillermo bought textbooks and notebooks at the bookstore. The number of textbooks was \(3\) more than twice the number of notebooks. He bought \(7\) textbooks. How many notebooks did he buy?
- Answer
-
\(2\)
Gerry worked Sudoku puzzles and crossword puzzles this week. The number of Sudoku puzzles he completed is eight more than twice the number of crossword puzzles. He completed \(22\) Sudoku puzzles. How many crossword puzzles did he do?
- Answer
-
\(7\)
Solve Number Problems
Now that we have a problem solving strategy, we will use it on several different types of word problems. The first type we will work on is “number problems.” Number problems give some clues about one or more numbers. We use these clues to write an equation. Number problems don’t usually arise on an everyday basis, but they provide a good introduction to practicing the problem solving strategy outlined above.
The difference of a number and six is \(13\). Find the number.
Solution
| Step 1. Read the problem. Are all the words familiar? | |
| Step 2. Identify what we are looking for. | the number |
| Step 3. Name. Choose a variable to represent the number. | Let \(n=\) the number. |
| Step 4. Translate. Remember to look for clue words like "difference... of... and..." | |
| Restate the problem as one sentence. | \(\color{cyan} \underbrace{\color{black}\textbf{The difference of the number and }\mathbf{6}} \quad \underbrace{\strut \color{black}\textbf{ is }} \quad \underbrace{\strut \color{black}\mathbf{13}}\) |
| Translate into an equation. | \(\qquad \qquad \qquad n-6 \qquad \qquad \qquad \quad = \quad 13\) |
| Step 5. Solve the equation. | \(\quad n - 6 = 13\) |
| Simplify. | \(\quad n =19\) |
| Step 6. Check. | |
| The difference of \(19\) and \(6\) is \(13\). It checks! | |
| Step 7. Answer the question. | The number is \(19\). |
The difference of a number and eight is \(17\). Find the number.
- Answer
-
\(25\)
The difference of a number and eleven is \(−7\). Find the number.
- Answer
-
\(4\)
The sum of twice a number and seven is \(15\). Find the number.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | the number |
| Step 3. Name. Choose a variable to represent the number. | Let \(n =\) the number. |
| Step 4. Translate. | |
| Restate the problem as one sentence. |  |
| Translate into an equation. |  |
| Step 5. Solve the equation. |  |
| Subtract 7 from each side and simplify. |  |
| Divide each side by 2 and simplify. |  |
| Step 6. Check. | |
| Is the sum of twice 4 and 7 equal to 15? | |
| \(\begin{array} {rrl} {2\cdot 4 + 7} &{\stackrel{?}{=}}& {15} \\ {15} &{=} &{15\checkmark} \end{array}\) | |
| Step 7. Answer the question. | The number is \(4\). |
The sum of four times a number and two is \(14\). Find the number.
- Answer
-
\(3\)
The sum of three times a number and seven is \(25\). Find the number.
- Answer
-
\(6\)
Some number word problems ask us to find two or more numbers. It may be tempting to name them all with different variables, but so far we have only solved equations with one variable. In order to avoid using more than one variable, we will define the numbers in terms of the same variable. Be sure to read the problem carefully to discover how all the numbers relate to each other.
One number is five more than another. The sum of the numbers is 21. Find the numbers.
Solution
| Step 1. Read the problem. | ||
| Step 2. Identify what we are looking for. | We are looking for two numbers. | |
| Step 3. Name. We have two numbers to name and need a name for each. | ||
| Choose a variable to represent the first number. | Let \(n=1^{st}\) number. | |
| What do we know about the second number? | One number is five more than another. | |
| \(n+5=2^{nd}\) number | ||
| Step 4. Translate. Restate the problem as one sentence with all the important information. | The sum of the 1st number and the 2nd number is 21. | |
| Translate into an equation. | 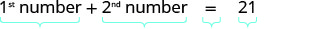 |
|
| Substitute the variable expressions. | 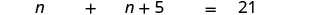 |
|
| Step 5. Solve the equation. | 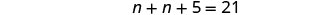 |
|
| Combine like terms. | 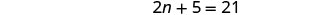 |
|
| Subtract 5 from both sides and simplify. |  |
|
| Divide by 2 and simplify. |  |
|
| Find the second number, too. |  |
|
 |
||
 |
||
| Step 6. Check. | ||
| Do these numbers check in the problem? | ||
| Is one number \(5\) more than the other? | \(13\stackrel{?}{=} 8 + 5\) | |
| Is thirteen \(5\) more than \(8\)? Yes. | \(13 = 13\checkmark\) | |
| Is the sum of the two numbers \(21\)? | \(8 + 13 \stackrel{?}{=} 21\) | |
| \(21 = 21\checkmark\) | ||
| Step 7. Answer the question. | The numbers are \(8\) and \(13\). |
One number is six more than another. The sum of the numbers is twenty-four. Find the numbers.
- Answer
-
9, 15
The sum of two numbers is fifty-eight. One number is four more than the other. Find the numbers.
- Answer
-
27, 31
The sum of two numbers is negative fourteen. One number is four less than the other. Find the numbers.
Solution
| Step 1. Read the problem. | ||
| Step 2. Identify what we are looking for. | We are looking for two numbers. | |
| Step 3. Name. | ||
| Choose a variable. | Let \(n=1^{st}\) number. | |
| One number is 4 less than the other. | \(n−4=2^{nd}\) number | |
| Step 4. Translate. | ||
| Write as one sentence. | The sum of the 2 numbers is negative 14. | |
| Translate into an equation. |  |
|
| Step 5. Solve the equation. |  |
|
| Combine like terms. | 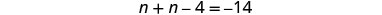 |
|
| Add 4 to each side and simplify. | 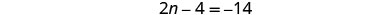 |
|
| Simplify. | 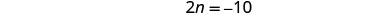 |
|
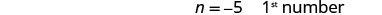 |
||
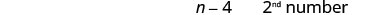 |
||
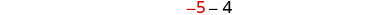 |
||
 |
||
| Step 6. Check. | ||
| Is −9 four less than −5? | \(-5-4\stackrel{?}{=}-9\) | |
| \(-9 = -9 \checkmark\) | ||
| Is their sum −14? | \(-5+ (-9)\stackrel{?}{=}-14\) | |
| \(-14 = -14 \checkmark\) | ||
| Step 7. Answer the question. | The numbers are −5 and −9. |
The sum of two numbers is negative twenty-three. One number is seven less than the other. Find the numbers.
- Answer
-
-15, -8
The sum of two numbers is \(−18\). One number is \(40\) more than the other. Find the numbers.
- Answer
-
-29, 11
One number is ten more than twice another. Their sum is one. Find the numbers.
Solution
| Step 1. Read the problem. | ||
| Step 2. Identify what you are looking for. | We are looking for two numbers. | |
| Step 3. Name. | ||
| Choose a variable. | Let \(x=1^{st}\) number. | |
| One number is 10 more than twice another. | \(2x+10=2^{nd}\) number | |
| Step 4. Translate. | ||
| Restate as one sentence. | Their sum is one. | |
| The sum of the two numbers is 1. | ||
| Translate into an equation. | 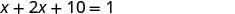 |
|
| Step 5. Solve the equation. | ||
| Combine like terms. | 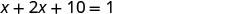 |
|
| Subtract 10 from each side. | 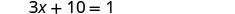 |
|
| Divide each side by 3. | 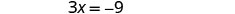 |
|
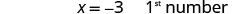 |
||
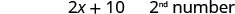 |
||
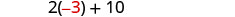 |
||
 |
||
| Step 6. Check. | ||
| Is ten more than twice −3 equal to 4? | \(2(-3) + 10 \stackrel{?}{=} 4\) | |
| \(-6 + 10 \stackrel{?}{=} 4\) | ||
| \(4 = 4\checkmark\) | ||
| Is their sum 1? | \(-3 + 4 \stackrel{?}{=} 1\) | |
| \(1 = 1\checkmark\) | ||
| Step 7. Answer the question. | The numbers are −3 and 4. |
One number is eight more than twice another. Their sum is negative four. Find the numbers.
- Answer
-
\(-4,\; 0\)
One number is three more than three times another. Their sum is \(−5\). Find the numbers.
- Answer
-
\(-3,\; -2\)
Some number problems involve consecutive integers. Consecutive integers are integers that immediately follow each other. Examples of consecutive integers are:
\[\begin{array}{l}{1,2,3,4} \\ {-10,-9,-8,-7} \\ {150,151,152,153}\end{array}\]
Notice that each number is one more than the number preceding it. So if we define the first integer as \(n\), the next consecutive integer is \(n+1\). The one after that is one more than \(n+1\), so it is \(n+1+1\), which is \(n+2\).
\[\begin{array}{ll}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text { consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]
The sum of two consecutive integers is \(47\). Find the numbers.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | two consecutive integers |
| Step 3. Name each number. | Let \(n=1^{st}\) integer. |
| \(n+1=\) next consecutive integer | |
| Step 4. Translate. | |
| Restate as one sentence. | The sum of the integers is \(47\). |
| Translate into an equation. |  |
| Step 5. Solve the equation. |  |
| Combine like terms. |  |
| Subtract 1 from each side. |  |
| Divide each side by 2. |  |
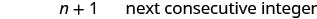 |
|
 |
|
 |
|
| Step 6. Check. | |
| \(\begin{array} {lll} {23 + 24} &{\stackrel{?}{=}} &{47} \\ {47} &{=} &{47\checkmark} \end{array}\) | |
| Step 7. Answer the question. | The two consecutive integers are 23 and 24. |
The sum of two consecutive integers is 95. Find the numbers.
- Answer
-
47, 48
The sum of two consecutive integers is −31. Find the numbers.
- Answer
-
-16, -15
Find three consecutive integers whose sum is −42.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | three consecutive integers |
| Step 3. Name each of the three numbers. | Let \(n=1^{st}\) integer. |
| \(n+1= 2^{nd}\) consecutive integer | |
| \(n+2= 3^{rd}\) consecutive integer | |
| Step 4. Translate. | |
| Restate as one sentence. | The sum of the three integers is \(−42\). |
| Translate into an equation. | 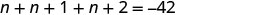 |
| Step 5. Solve the equation. | 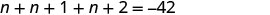 |
| Combine like terms. | 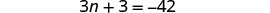 |
| Subtract 3 from each side. | 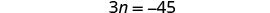 |
| Divide each side by 3. | 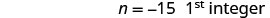 |
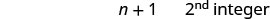 |
|
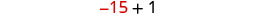 |
|
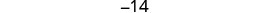 |
|
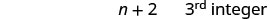 |
|
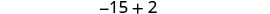 |
|
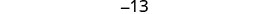 |
|
| Step 6. Check. | |
| \(\begin{array}{lll} {-13 + (-14) + (-15)} &{\stackrel{?}{=}} &{-42} \\ {-42} &{=} &{-42\checkmark} \end{array}\) | |
| Step 7. Answer the question. | The three consecutive integers are −13, −14, and −15. |
Find three consecutive integers whose sum is −96.
- Answer
-
-33, -32, -31
Find three consecutive integers whose sum is −36.
- Answer
-
-13, -12, -11
Now that we have worked with consecutive integers, we will expand our work to include consecutive even integers and consecutive odd integers. Consecutive even integers are even integers that immediately follow one another. Examples of consecutive even integers are:
\[\begin{array}{l}{18,20,22} \\ {64,66,68} \\ {-12,-10,-8}\end{array}\]
Notice each integer is \(2\) more than the number preceding it. If we call the first one \(n\), then the next one is \(n+2\). The next one would be \(n+2+2\) or \(n+4\).
\[\begin{array}{cll}{n} & {1^{\text { st }} \text { even integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]
Consecutive odd integers are odd integers that immediately follow one another. Consider the consecutive odd integers \(77\), \(79\), and \(81\).
\[\begin{array}{l}{77,79,81} \\ {n, n+2, n+4}\end{array}\]
\[\begin{array}{cll}{n} & {1^{\text { st }} \text {odd integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]
Does it seem strange to add 2 (an even number) to get from one odd integer to the next? Do you get an odd number or an even number when we add 2 to 3? to 11? to 47?
Whether the problem asks for consecutive even numbers or odd numbers, you don’t have to do anything different. The pattern is still the same—to get from one odd or one even integer to the next, add 2.
Find three consecutive even integers whose sum is 84.
Solution
\[\begin{array}{ll} {\textbf{Step 1. Read} \text{ the problem.}} & {} \\ {\textbf{Step 2. Identify} \text{ what we are looking for.}} & {\text{three consecutive even integers}} \\ {\textbf{Step 3. Name} \text{ the integers.}} & {\text{Let } n = 1^{st} \text{ even integers.}} \\ {} &{n + 2 = 2^{nd} \text{ consecutive even integer}} \\ {} &{n + 4 = 3^{rd} \text{ consecutive even integer}} \\ {\textbf{Step 4. Translate.}} &{} \\ {\text{ Restate as one sentence. }} &{\text{The sum of the three even integers is 84.}} \\ {\text{Translate into an equation.}} &{n + n + 2 + n + 4 = 84} \\ {\textbf{Step 5. Solve} \text{ the equation. }} &{} \\ {\text{Combine like terms.}} &{n + n + 2 + n + 4 = 84} \\ {\text{Subtract 6 from each side.}} &{3n + 6 = 84} \\ {\text{Divide each side by 3.}} &{3n = 78} \\ {} &{n = 26 \space 1^{st} \text{ integer}} \\\\ {} &{n + 2\space 2^{nd} \text{ integer}} \\ {} &{26 + 2} \\ {} &{28} \\\\ {} &{n + 4\space 3^{rd} \text{ integer}} \\ {} &{26 + 4} \\ {} &{30} \\ {\textbf{Step 6. Check.}} &{} \\\\ {26 + 28 + 30 \stackrel{?}{=} 84} &{} \\ {84 = 84 \checkmark} & {} \\ {\textbf{Step 7. Answer} \text{ the question.}} &{\text{The three consecutive integers are 26, 28, and 30.}} \end{array}\]
Find three consecutive even integers whose sum is 102.
- Answer
-
32, 34, 36
Find three consecutive even integers whose sum is −24.
- Answer
-
−10,−8,−6
A married couple together earns $110,000 a year. The wife earns $16,000 less than twice what her husband earns. What does the husband earn?
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what we are looking for. | How much does the husband earn? |
| Step 3. Name. | |
| Choose a variable to represent the amount the husband earns. |
Let \(h=\) the amount the husband earns. |
| The wife earns \($16,000\) less than twice that. | \(2h−16,000\) the amount the wife earns. |
| Step 4. Translate. | Together the husband and wife earn \($110,000\). |
| Restate the problem in one sentence with all the important information. |
 |
| Translate into an equation. | 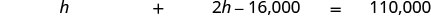 |
| Step 5. Solve the equation. | \(h + 2h − 16,000 = 110,000\) |
| Combine like terms. | \(3h − 16,000 = 110,000\) |
| Add \(16,000\) to both sides and simplify. | \(3h = 126,000\) |
| Divide each side by \(3\). | \(h = 42,000\) |
| \($42,000\) amount husband earns | |
| \(2h − 16,000\) amount wife earns | |
| \(2(42,000) − 16,000\) | |
| \(84,000 − 16,000\) | |
| \(68,000\) | |
| Step 6. Check. | |
| If the wife earns \($68,000 \) and the husband earns \($42,000 \) is the total \($110,000 \) ? Yes! | |
| Step 7. Answer the question. | The husband earns \($42,000 \) a year. |
According to the National Automobile Dealers Association, the average cost of a car in 2014 was $28,500. This was $1,500 less than 6 times the cost in 1975. What was the average cost of a car in 1975?
- Answer
-
$5000
U.S. Census data shows that the median price of new home in the United States in November 2014 was $280,900. This was $10,700 more than 14 times the price in November 1964. What was the median price of a new home in November 1964?
- Answer
-
$19300
Key Concepts
- Problem-Solving Strategy
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
- Consecutive Integers
Consecutive integers are integers that immediately follow each other.\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+1} & {2^{\text { nd }} \text {consecutive integer }} \\ {n+2} & {3^{\text { rd }} \text { consecutive integer } \ldots \text { etc. }}\end{array}\]
Consecutive even integers are even integers that immediately follow one another.\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive even integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive even integer } \ldots \text { etc. }}\end{array}\]
Consecutive odd integers are odd integers that immediately follow one another.\[\begin{array}{cc}{n} & {1^{\text { st }} \text { integer }} \\ {n+2} & {2^{\text { nd }} \text { consecutive odd integer }} \\ {n+4} & {3^{\text { rd }} \text { consecutive odd integer } \ldots \text { etc. }}\end{array}\]


