6.7E: Exercises

Last updated
Save as PDF

Page ID: 30258

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Practice Makes Perfect

Use the Definition of a Negative Exponent

In the following exercises, simplify.

Exercise 1

$4^{−2}$
$10^{−3}$

Exercise 2

$3^{−4}$
$10^{−2}$

Answer

$\frac{1}{81}$
$\frac{1}{100}$

Exercise 3

$5^{−3}$
$10^{−5}$

Exercise 4

$2^{−8}$
$10^{−2}$

Answer

$\frac{1}{256}$
$\frac{1}{100}$

Exercise 5

$\dfrac{1}{c^{−5}}$
$\dfrac{1}{3^{−2}}$

Exercise 6

$\dfrac{1}{c^{−5}}$
$\dfrac{1}{5^{−2}}$

Answer

$c^5$
25

Exercise 7

$\dfrac{1}{q^{−10}}$
$\dfrac{1}{10^{−3}}$

Exercise 8

$\dfrac{1}{t^{−9}}$
$\dfrac{1}{10^{−4}}$

Answer

$t^9$
$10000$

Exercise 9

$\left(\dfrac{5}{8}\right)^{−2}$
$\left(−\dfrac{3m}{n}\right)^{−2}$

Exercise 10

$\left(\dfrac{3}{10}\right)^{−2}$
$\left(−\dfrac{2c}{d}\right)^{−3}$

Answer

$\dfrac{100}{9}$
$−\dfrac{d^3}{8c^3}$

Exercise 11

$\left(\dfrac{4}{9}\right)^{−3}$
$\left(−\dfrac{u^2}{2v}\right)^{−5}$

Exercise 12

$\left(\dfrac{7}{2}\right)^{−3}$
$\left(−\dfrac{3}{xy^2}\right)^{−3}$

Answer

$\dfrac{8}{343}$
$−\dfrac{x^{3}y^6}{27}$

Exercise 13

$(−5)^{−2}$
$−5^{−2}$
$\left(−\frac{1}{5}\right)^{−2}$
$−\left(\frac{1}{5}\right)^{−2}$

Exercise 14

$(−7)^{−2}$
$−7^{−2}$
$\left(−\frac{1}{7}\right)^{−2}$
$−\left(\frac{1}{7}\right)^{−2}$

Answer

$\frac{1}{49}$
$−\frac{1}{49}$
49
−49

Exercise 15

$−3^{−3}$
$\left(−\frac{1}{3}\right)^{−3}$
$−\left(\frac{1}{3}\right)^{−3}$
$(−3)^{−3}$

Exercise 16

$−5^{−3}$
$\left(−\frac{1}{5}\right)^{−3}$
$−\left(\frac{1}{5}\right)^{−3}$
$(−5)^{−3}$

Answer

$−\frac{1}{125}$
−125
−125
$−\frac{1}{125}$

Exercise 17

$3·5^{−1}$
$(3·5)^{−1}$

Exercise 18

$2·5^{−1}$
$(2·5)^{−1}$

Answer

$\frac{2}{5}$
$\frac{1}{10}$

Exercise 19

$4·5^{−2}$
$(4·5)^{−2}$

Exercise 20

$3·4^{−2}$
$(3·4)^{−2}$

Answer

$\frac{3}{16}$
$\frac{1}{144}$

Exercise 21

$m^{−4}$
$(x^3)^{−4}$

Exercise 22

$b^{−5}$
$(k^2)^{−5}$

Answer

$\dfrac{1}{b^5}$
$\dfrac{1}{k^{10}}$

Exercise 23

$p^{−10}$
$(q^6)^{−8}$

Exercise 24

$s^{−8}$
$(a^9)^{−10}$

Answer

$\dfrac{1}{s^8}$
$\dfrac{1}{a^{90}}$

Exercise 25

$7n^{−1}$
$(7n)^{−1}$
$(−7n)^{−1}$

Exercise 26

$6r^{−1}$
$(6r)^{−1}$
$(−6r)^{−1}$

Answer

$\dfrac{6}{r}$
$\dfrac{1}{6r}$
$−\dfrac{1}{6r}$

Exercise 27

$(3p)^{−2}$
$3p^{−2}$
$−3p^{−2}$

Exercise 28

$(2q)^{−4}$
$2q^{−4}$
$−2q^{−4}$

Answer

$\dfrac{1}{16q^4}$
$\dfrac{2}{q^4}$
$−\dfrac{2}{q^4}$

Simplify Expressions with Integer Exponents

In the following exercises, simplify.

Exercise 29

$b^{4}b^{−8}$
$r^{−2}r^5$
$x^{−7}x^{−3}$

Exercise 30

$s^3·s^{−7}$
$q^{−8}·q^3$
$y^{−2}·y^{−5}$

Answer

$\dfrac{1}{s^4}$
$\dfrac{1}{q^5}$
$\dfrac{1}{y^7}$

Exercise 31

$a^3·a^{−3}$
$a·a^3$
$a·a^{−3}$

Exercise 32

$y^5·y^{−5}$
$y·y^5$
$y·y^{−5}$

Answer

1
$y^6$
$\dfrac{1}{y^4}$

Exercise 33

$p^5·p^{−2}·p^{−4}$

Exercise 34

$x^4·x^{−2}·x^{−3}$

Answer: $\dfrac{1}{x}$

Exercise 35

$(w^{4}x^{−5})(w^{−2}x^{−4})$

Exercise 36

$(m^{3}n^{−3})(m^{−5}n^{−1})$

Answer: $\dfrac{1}{m^{2}n^4}$

Exercise 37

$(uv^{−2})(u^{−5}v^{−3})$

Exercise 38

$(pq^{−4})(p^{−6}q^{−3})$

Answer: $\dfrac{1}{p^{5}q^{7}}$

Exercise 39

$(−6c^{−3}d^9)(2c^{4}d^{−5})$

Exercise 40

$(−2j^{−5}k^8)(7j^{2}k^{−3})$

Answer: $−\dfrac{14k^5}{j^3}$

Exercise 41

$(−4r^{−2}s^{−8})(9r^{4}s^3)$

Exercise 42

$(−5m^{4}n^6)(8m^{−5}n^{−3})$

Answer: $−\dfrac{40n^3}{m}$

Exercise 43

$(5x^2)^{−2}$

Exercise 44

$(4y^3)^{−3}$

Answer: $\dfrac{1}{64y^9}$

Exercise 45

$(3z^{−3})^2$

Exercise 46

$(2p^{−5})^2$

Answer: $\dfrac{4}{p^{10}}$

Exercise 47

$\dfrac{t^{9}}{t^{−3}}$

Exercise 48

$\dfrac{n^{5}}{n^{−2}}$

Answer: $n^7$

Exercise 49

$\dfrac{x^{−7}}{x^{−3}}$

Exercise 50

$\dfrac{y^{−5}}{y^{−10}}$

Answer: $y^5$

Convert from Decimal Notation to Scientific Notation

In the following exercises, write each number in scientific notation.

Exercise 51

57,000

Exercise 52

340,000

Answer: $3.4 \times 10^{5}$

Exercise 53

8,750,000

Exercise 54

1,290,000

Answer: $1.29 \times 10^{6}$

Exercise 55

0.026

Exercise 56

0.041

Answer: $4.1 \times 10^{-2}$

Exercise 57

0.00000871

Exercise 58

0.00000103

Answer: $1.03 \times 10^{-6}$

Convert Scientific Notation to Decimal Form

In the following exercises, convert each number to decimal form.

Exercise 59

$5.2 \times 10^{2}$

Exercise 60

$8.3 \times 10^{2}$

Answer: 830

Exercise 61

$7.5 \times 10^{6}$

Exercise 62

$1.6 \times 10^{10}$

Answer: 16,000,000,000

Exercise 63

$2.5 \times 10^{-2}$

Exercise 64

$3.8 \times 10^{-2}$

Answer: 0.038

Exercise 65

$4.13 \times 10^{-5}$

Exercise 66

$1.93 \times 10^{-5}$

Answer: 0.0000193

Multiply and Divide Using Scientific Notation

In the following exercises, multiply. Write your answer in decimal form.

Exercise 67

$\left(3 \times 10^{-5}\right)\left(3 \times 10^{9}\right)$

Exercise 68

$\left(2 \times 10^{2}\right)\left(1 \times 10^{-4}\right)$

Answer: 0.02

Exercise 69

$\left(7.1 \times 10^{-2}\right)\left(2.4 \times 10^{-4}\right)$

Exercise 70

$\left(3.5 \times 10^{-4}\right)\left(1.6 \times 10^{-2}\right)$

Answer: $5.6 \times 10^{-6}$

In the following exercises, divide. Write your answer in decimal form.

Exercise 71

$\dfrac{7 \times 10^{-3}}{1 \times 10^{-7}}$

Exercise 72

$\dfrac{5 \times 10^{-2}}{1 \times 10^{-10}}$

Answer: 500,000,000

Exercise 73

$\dfrac{6 \times 10^{4}}{3 \times 10^{-2}}$

Exercise 74

$\dfrac{8 \times 10^{6}}{4 \times 10^{-1}}$

Answer: 20,000,000

Everyday Math

Exercise 75

The population of the United States on July 4, 2010 was almost 310,000,000. Write the number in scientific notation.

Exercise 76

The population of the world on July 4, 2010 was more than 6,850,000,000. Write the number in scientific notation

Answer: $6.85 \times 10^{9}$

Exercise 77

The average width of a human hair is 0.0018 centimeters. Write the number in scientific notation.

Exercise 78

The probability of winning the 2010 Megamillions lottery was about 0.0000000057. Write the number in scientific notation.

Answer: $5.7 \times 10^{-9}$

Exercise 79

In $2010,$ the number of Facebook users each day who changed their status to 'engaged" was $2 \times 10^{4} .$ Convert this number
to decimal form.

Exercise 80

At the start of $2012,$ the US federal budget had a deficit of more than $\$ 1.5 \times 10^{13} .$ Convert this number to decimal form.

Answer: 15,000,000,000,000

Exercise 81

The concentration of carbon dioxide in the atmosphere is $3.9 \times 10^{-4} .$ Convert this number to decimal form.

Exercise 82

The width of a proton is $1 \times 10^{-5}$ of the width of an atom. Convert this number to decimal form.

Answer: 0.00001

Exercise 83

Health care costs The Centers for Medicare and Medicaid projects that consumers will spend more than $4 trillion on health care by 2017.

Write 4 trillion in decimal notation.
Write 4 trillion in scientific notation.

Exercise 84

Coin production In 1942, the U.S. Mint produced 154,500,000 nickels. Write 154,500,000 in scientific notation.

Answer: $1.545 \times 10^{8}$

Exercise 85

Distance The distance between Earth and one of the brightest stars in the night star is 33.7 light years. One light year is about 6,000,000,000,000 (6 trillion), miles.

Write the number of miles in one light year in scientific notation.
Use scientific notation to find the distance between Earth and the star in miles. Write the answer in scientific notation.

Exercise 86

Debt At the end of fiscal year 2015 the gross United States federal government debt was estimated to be approximately $18,600,000,000,000 ($18.6 trillion), according to the Federal Budget. The population of the United States was approximately 300,000,000 people at the end of fiscal year 2015.

Write the debt in scientific notation.
Write the population in scientific notation.
Find the amount of debt per person by using scientific notation to divide the debt by the population. Write the answer in scientific notation.

Answer

$1.86 \times 10^{13}$
$3 \times 10^{8}$
$6.2 \times 10^{4}$

Writing Exercises

Exercise 87

Explain the meaning of the exponent in the expression $2^{3}$.
Explain the meaning of the exponent in the expression $2^{-3}$.

Exercise 88

When you convert a number from decimal notation to scientific notation, how do you know if the exponent will be positive or negative?

Answer: answers will vary

Self Check

a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

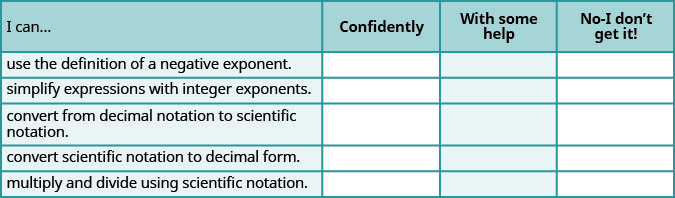
$This is a table that has six rows and four columns. In the first row, which is a header row, the cells read from left to right “I can…,” “Confidently,” “With some help,” and “No-I don’t get it!” The first column below “I can…” reads “use the definition of a negative exponent,” “simplify expressions with integer exponents,” “convert from decimal notation to scientific notation,” “convert scientific notation to decimal form,” and “multiply and divide using scientific notation.” The rest of the cells are blank.$

b. Overall, after looking at the checklist, do you think you are well-prepared for the next section? Why or why not?