6.7: Integer Exponents and Scientific Notation

Learning Objectives

By the end of this section, you will be able to:

• Use the definition of a negative exponent
• Simplify expressions with integer exponents
• Convert from decimal notation to scientific notation
• Convert scientific notation to decimal form
• Multiply and divide using scientific notation

Note

Before you get started, take this readiness quiz.

1. What is the place value of the 6 in the number 64891?
   If you missed this problem, review Example 1.2.1.
2. Name the decimal: 0.0012.
   If you missed this problem, review Example 1.8.1.
3. Subtract: 5−(−3).
   If you missed this problem, review Example 1.4.33.

Use the Definition of a Negative Exponent

We saw that the Quotient Property for Exponents introduced earlier in this chapter, has two forms depending on whether the exponent is larger in the numerator or the denominator.

QUOTIENT PROPERTY FOR EXPONENTS

If a is a real number, $a\neq0$, and m and n are whole numbers, then

$$\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \quad$$

and

$$\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m$$

What if we just subtract exponents regardless of which is larger?

Let’s consider $\dfrac{x^{2}}{x^{5}}$.

We subtract the exponent in the denominator from the exponent in the numerator.

$$\begin{array}{c}{\dfrac{x^{2}}{x^{5}}} \\ {x^{2-5}} \\ {x^{-3}}\end{array}$$

We can also simplify $\dfrac{x^{2}}{x^{5}}$ by dividing out common factors:

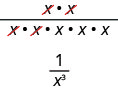
This implies that $x^{-3}=\dfrac{1}{x^{3}}$ and it leads us to the definition of a negative exponent.

Definition: NEGATIVE EXPONENT

If n is an integer and $a\neq 0$, then $a^{-n}=\dfrac{1}{a^{n}}$

The negative exponent tells us we can re-write the expression by taking the reciprocal of the base and then changing the sign of the exponent.

Any expression that has negative exponents is not considered to be in simplest form. We will use the definition of a negative exponent and other properties of exponents to write the expression with only positive exponents.

For example, if after simplifying an expression we end up with the expression $x^{-3}$, we will take one more step and write $\dfrac{1}{x^{3}}$. The answer is considered to be in simplest form when it has only positive exponents.

Example $\PageIndex{1}$

Simplify:

1. $4^{-2}$
2. $10^{-3}$

Solution

$\begin{array}{lll} 1. && 4^{-2} \\& {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & {\dfrac{1}{4^{2}}} \\& {\text { Simplify. }} & \dfrac{1}{16} \end{array}$

$\begin{array}{lll} \\ 2. && 10^{-3} \\& {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & \dfrac{1}{10^{3}} \\& {\text { Simplify. }} & \dfrac{1}{1000}\end{array}$

Try It $\PageIndex{2}$

Simplify:

1. $2^{-3}$
2. $10^{-7}$

Answer

1. $\dfrac{1}{8}$
2. $\dfrac{1}{10^{7}}$

Try It $\PageIndex{3}$

Simplify:

1. $3^{-2}$
2. $10^{-4}$

Answer

1. $\dfrac{1}{9}$
2. $\dfrac{1}{10,000}$

In Example $\PageIndex{1}$ we raised an integer to a negative exponent. What happens when we raise a fraction to a negative exponent? We’ll start by looking at what happens to a fraction whose numerator is one and whose denominator is an integer raised to a negative exponent.

$\begin{array}{ll}& \dfrac{1}{a^{-n}}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\dfrac{1}{a^{n}}} \\ {\text { Simplify the complex fraction. }} & 1 \cdot \dfrac{a^{n}}{1}\\ {\text { Multiply. }} & a^{n}\end{array}$

This leads to the Property of Negative Exponents.

PROPERTY OF NEGATIVE EXPONENTS

If n is an integer and $a\neq 0$, then $\dfrac{1}{a^{-n}}=a^{n}$.

Example $\PageIndex{4}$

Simplify:

1. $\dfrac{1}{y^{-4}}$
2. $\dfrac{1}{3^{-2}}$

Solution

$\begin{array} { lll } 1. && \dfrac{1}{y^{-4}}\\& \text { Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & y^{4}\end{array}$

$\begin{array} { lll } \\ 2. && \dfrac{1}{3^{-2}}\\& \text {Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & 3^{2} \\& \text{Simplify.}& 9\end{array}$

Try It $\PageIndex{5}$

Simplify:

1. $\dfrac{1}{p^{-8}}$
2. $\dfrac{1}{4^{-3}}$

Answer

1. $p^{8}$
2. 64

Try It $\PageIndex{6}$

Simplify:

1. $\dfrac{1}{q^{-7}}$
2. $\dfrac{1}{2^{-4}}$

Answer

1. $q^{7}$
2. 16

Suppose now we have a fraction raised to a negative exponent. Let’s use our definition of negative exponents to lead us to a new property.

$\begin{array}{ll}& \left(\dfrac{3}{4}\right)^{-2}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\left(\dfrac{3}{4}\right)^{2}} \\ {\text { Simplify the denominator. }} & \dfrac{1}{\dfrac{9}{16}}\\ {\text { Simplify the complex fraction.}} &\dfrac{16}{9}\\ \text { But we know that } \dfrac{16}{9} \text { is }\left(\dfrac{4}{3}\right)^{2} & \\ \text { This tells us that: } & \left(\dfrac{3}{4}\right)^{-2}=\left(\dfrac{4}{3}\right)^{2}\end{array}$

To get from the original fraction raised to a negative exponent to the final result, we took the reciprocal of the base—the fraction—and changed the sign of the exponent.

This leads us to the Quotient to a Negative Power Property.

QUOTIENT TO A NEGATIVE EXPONENT PROPERTY

If $a$ and $b$ are real numbers, $a \neq 0, b \neq 0,$ and $n$ is an integer, then $\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}$

Example $\PageIndex{7}$

Simplify:

1. $\left(\dfrac{5}{7}\right)^{-2}$
2. $\left(-\dfrac{2 x}{y}\right)^{-3}$

Solution

$\begin{array}{lll}1. && \left(\dfrac{5}{7}\right)^{-2}\\ & \begin{array}{l} {\text {Use the Quotient to a Negative Exponent Property, } } \\ { \left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n} \text {. Take the reciprocal of the } } \\ {\text {fraction and change the sign of the exponent. }. } \end{array} &\left(\dfrac{7}{5}\right)^{2}\\ & \text { Simplify. } & \dfrac{49}{25}\end{array}$

$\begin{array}{lll}\\2. && \left(-\dfrac{2 x}{y}\right)^{-3}\\ & \begin{array}{l} {\text {Use the Quotient to a Negative Exponent Property, } } \\ { \left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n} \text {. Take the reciprocal of the } } \\ {\text {fraction and change the sign of the exponent. } } \end{array} &\left(-\dfrac{y}{2 x}\right)^{3}\\ & \text { Simplify. } & -\dfrac{y^{3}}{8 x^{3}}\end{array}$

Try It $\PageIndex{8}$

Simplify:

1. $\left(\dfrac{2}{3}\right)^{-4}$
2. $\left(-\dfrac{6 m}{n}\right)^{-2}$

Answer

1. $\dfrac{81}{16}$
2. $\dfrac{n^{2}}{36 m^{2}}$

Try It $\PageIndex{9}$

Simplify:

1. $\left(\dfrac{3}{5}\right)^{-3}$
2. $\left(-\dfrac{a}{2 b}\right)^{-4}$

Answer

1. $\dfrac{125}{27}$
2. $\dfrac{16 b^{4}}{a^{4}}$

When simplifying an expression with exponents, we must be careful to correctly identify the base.

Example $\PageIndex{10}$

Simplify:

1. $(-3)^{-2}$
2. $-3^{-2}$
3. $\left(-\dfrac{1}{3}\right)^{-2}$
4. $-\left(\dfrac{1}{3}\right)^{-2}$

Solution

1. Here the exponent applies to the base −3.

$\begin{array}{ll} & (-3)^{-2}\\ \begin{array}{l} {\text { Take the reciprocal of the base } }\\ {\text { and change the sign of the exponent}. } \end{array} & \dfrac{1}{(-3)^{2}} \\ {\text { Simplify. }} & \dfrac{1}{9}\end{array}$

2. The expression $-3^{-2}$ means “find the opposite of $3^{-2}$”. Here the exponent applies to the base 3.

$\begin{array}{ll} &-3^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot 3^{-2}\\ \begin{array}{l} {\text { Take the reciprocal of the base } }\\ {\text { and change the sign of the exponent}. } \end{array} & -1 \cdot \dfrac{1}{3^{2}}\\ {\text { Simplify. }} & -\dfrac{1}{9}\end{array}$

3. Here the exponent applies to the base$\left(-\frac{1}{3}\right)$.

$\begin{array}{ll} &\left(-\dfrac{1}{3}\right)^{-2}\\ \begin{array}{l} {\text { Take the reciprocal of the base } }\\ {\text { and change the sign of the exponent}. } \end{array} & \left(-\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & 9\end{array}$

4. The expression $-\left(\frac{1}{3}\right)^{-2}$ means “find the opposite of $\left(\frac{1}{3}\right)^{-2}$”. Here the exponent applies to the base $\left(\frac{1}{3}\right)$.

$\begin{array}{ll} &-\left(\dfrac{1}{3}\right)^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot\left(\dfrac{1}{3}\right)^{-2}\\ \begin{array}{l} {\text { Take the reciprocal of the base } }\\ {\text { and change the sign of the exponent}. } \end{array} & -1 \cdot\left(\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & -9 \end{array}$

Try It $\PageIndex{11}$

Simplify:

1. $(-5)^{-2}$
2. $-5^{-2}$
3. $\left(-\dfrac{1}{5}\right)^{-2}$
4. $-\left(\dfrac{1}{5}\right)^{-2}$

Answer

1. $\dfrac{1}{25}$
2. $-\dfrac{1}{25}$
3. $25$
4. $−25$

Try It $\PageIndex{12}$

Simplify:

1. $(-7)^{-2}$
2. $-7^{-2}$
3. $\left(-\dfrac{1}{7}\right)^{-2}$
4. $-\left(\dfrac{1}{7}\right)^{-2}$

Answer

1. $\dfrac{1}{49}$
2. $-\dfrac{1}{49}$
3. $49$
4. $−49$

We must be careful to follow the Order of Operations. In the next example, parts (a) and (b) look similar, but the results are different.

Example $\PageIndex{13}$

Simplify:

1. 4$\cdot 2^{-1}$
2. $(4 \cdot 2)^{-1}$

Solution

$\begin{array}{lll} 1. &\text { Do exponents before multiplication. }&4 \cdot 2^{-1}\\& \text { Use } a^{-n}=\dfrac{1}{a^{n}}&4 \cdot \dfrac{1}{2^{1}}\\& {\text { Simplify. }} & 2 \end{array}$

$\begin{array}{lll} \\2. &&(4 \cdot 2)^{-1}\\& \text { Simplify inside the parentheses first. }&(8)^{-1}\\& \text { Use } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{8^{1}}\\&{\text { Simplify. }} & \dfrac{1}{8} \end{array}$

Try It $\PageIndex{14}$

Simplify:

1. 6$\cdot 3^{-1}$
2. $(6 \cdot 3)^{-1}$

Answer

1. $2$
2. $\dfrac{1}{18}$

Try It $\PageIndex{15}$

Simplify:

1. 8$\cdot 2^{-2}$
2. $(8 \cdot 2)^{-2}$

Answer

1. $2$
2. $\dfrac{1}{256}$

When a variable is raised to a negative exponent, we apply the definition the same way we did with numbers. We will assume all variables are non-zero.

Example $\PageIndex{16}$

Simplify:

1. $x^{-6}$
2. $\left(u^{4}\right)^{-3}$

Solution

$\begin{array}{lll}1. & &x^{-6}\\& \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{x^{6}}\end{array}$

$\begin{array}{lll} \\ 2. &\left(u^{4}\right)^{-3}\\& \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{\left(u^{4}\right)^{3}} \\& \text{ Simplify.} & \dfrac{1}{u^{12}}\end{array}$

Try It $\PageIndex{17}$

Simplify:

1. $y^{-7}$
2. $\left(z^{3}\right)^{-5}$

Answer

1. $\dfrac{1}{y^{7}}$
2. $\dfrac{1}{z^{15}}$

Try It $\PageIndex{18}$

Simplify:

1. $p^{-9}$
2. $\left(q^{4}\right)^{-6}$

Answer

1. $\dfrac{1}{p^{9}}$
2. $\dfrac{1}{q^{24}}$

When there is a product and an exponent we have to be careful to apply the exponent to the correct quantity. According to the Order of Operations, we simplify expressions in parentheses before applying exponents. We’ll see how this works in the next example.

Example $\PageIndex{19}$

Simplify:

1. $5 y^{-1}$
2. $(5 y)^{-1}$
3. $(-5 y)^{-1}$

Solution

1. Notice the exponent applies to just the base $y$.

$\begin{array}{ll} & 5 y^{-1}\\ \begin{array}{l} {\text { Take the reciprocal of the base } y, } \\ {\text { and change the sign of the exponent}. } \end{array} &5 \cdot \dfrac{1}{y^{1}} \\ \text { Simplify. } & \dfrac{5}{y}\end{array}$

2. Here the parentheses make the exponent apply to the base $5y$

$\begin{array}{ll} &(5 y)^{-1}\\ \begin{array}{l} {\text { Take the reciprocal of the base } 5y, }\\ {\text { and change the sign of the exponent}. } \end{array} &\dfrac{1}{(5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{5 y} \end{array}$

3. The base here is $-5 y$

$\begin{array}{ll} &(-5 y)^{-1}\\ \begin{array}{l} {\text { Take the reciprocal of the base }-5 y }\\ {\text { and change the sign of the exponent}. } \end{array} & \dfrac{1}{(-5 y)^{1}} \\ \text { Simplify. } & \dfrac{1}{-5 y} \\ \text { Use } \dfrac{a}{-b}=-\dfrac{a}{b} & -\dfrac{1}{5 y} \end{array}$

Try It $\PageIndex{20}$

Simplify:

1. $8 p^{-1}$
2. $(8 p)^{-1}$
3. $(-8 p)^{-1}$

Answer

1. $\dfrac{8}{p}$
2. $\dfrac{1}{8 p}$
3. $-\dfrac{1}{8 p}$

Try It $\PageIndex{21}$

Simplify:

1. $11 q^{-1}$
2. $(11 q)^{-1}$
3. $(-11 q)^{-1}$

Answer

1. $\dfrac{11}{q}$
2. $\dfrac{1}{11 q}$
3. $-\dfrac{1}{11 q}$

With negative exponents, the Quotient Rule needs only one form $\dfrac{a^{m}}{a^{n}}=a^{m-n},$ for $a \neq 0$. When the exponent in the denominator is larger than the exponent in the numerator, the exponent of the quotient will be negative.

Simplify Expressions with Integer Exponents

All of the exponent properties we developed earlier in the chapter with whole number exponents apply to integer exponents, too. We restate them here for reference.

SUMMARY OF EXPONENT PROPERTIES

If $a$ and $b$ are real numbers, and $m$ and $n$ are integers, then

$\begin{array}{lrll}{\textbf { Product Property }}& a^{m} \cdot a^{n} &=&a^{m+n} \\ {\textbf { Power Property }} &\left(a^{m}\right)^{n} &=&a^{m \cdot n} \\ {\textbf { Product to a Power }} &(a b)^{m} &=&a^{m} b^{m} \\ {\textbf { Quotient Property }} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, \quad a \neq 0 \\ {\textbf { Zero Exponent Property }}& \quad a^{0} &= & 1, \quad a \neq 0 \\ {\textbf { Quotient to a Power Property }} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}},\quad b \neq 0 \\ {\textbf { Properties of Negative Exponents }} & a^{-n} &=&\dfrac{1}{a^{n}} \text { and } \dfrac{1}{a^{-n}}=a^{n}\\ {\textbf { Quotient to a Negative Exponents }}& \left(\dfrac{a}{b}\right)^{-n} &=&\left(\dfrac{b}{a}\right)^{n} \\\end{array}$

Example $\PageIndex{22}$

Simplify:

1. $x^{-4} \cdot x^{6}$
2. $y^{-6} \cdot y^{4}$
3. $z^{-5} \cdot z^{-3}$

Solution

$\begin{array}{lll} 1. && x^{-4} \cdot x^{6} \\ & \text { Use the Product Property, } a^{m} \cdot a^{n}=a^{m+n} & x^{-4+6} \\ & \text { Simplify. } & x^{2} \end{array}$

$\begin{array}{lll} \\2. && y^{-6} \cdot y^{4} \\ & \text { Notice the same bases, so add the exponents. }& y^{-6+4}\\& \text { Simplify. } & y^{-2} \\ & \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{y^{2}} \end{array}$

$\begin{array}{lll} \\3. && z^{-5} \cdot z^{-3} \\ & \text { Add the exponents, since the bases are the same. }& z^{-5-3}\\ & \text { Simplify. } & z^{-8}\\ & \begin{array}{l} {\text {Use the definition of a negative exponent } }\\ {\text { to take the reciprocal of the base } }\\ {\text { and change the sign of the exponent}. } \end{array} & \dfrac{1}{z^{8}} \\ \end{array}$

Try It $\PageIndex{23}$

Simplify:

1. $x^{-3} \cdot x^{7}$
2. $y^{-7} \cdot y^{2}$
3. $z^{-4} \cdot z^{-5}$

Answer

1. $x^{4}$
2. $\dfrac{1}{y^{5}}$
3. $\dfrac{1}{z^{9}}$

Try It $\PageIndex{24}$

Simplify:

1. $a^{-1} \cdot a^{6}$
2. $b^{-8} \cdot b^{4}$
3. $c^{-8} \cdot c^{-7}$

Answer

1. $a^{5}$
2. $\dfrac{1}{b^{4}}$
3. $\dfrac{1}{c^{15}}$

In the next two examples, we’ll start by using the Commutative Property to group the same variables together. This makes it easier to identify the like bases before using the Product Property.

Example $\PageIndex{25}$

Simplify: $\left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right)$

Solution

$\begin{array}{ll}& \left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right) \\ \text { Use the Commutative Property to get like bases together. }& m^{4} m^{-5} \cdot n^{-2} n^{-3}\\ \text { Add the exponents for each base. }&m^{-1} \cdot n^{-5}\\ \text { Take reciprocals and change the signs of the exponents. }& \dfrac{1}{m^{1}} \cdot \dfrac{1}{n^{5}} \\ \text { Simplify. } & \dfrac{1}{m n^{5}}\end{array}$

Try It $\PageIndex{26}$

Simplify: $\left(p^{6} q^{-2}\right)\left(p^{-9} q^{-1}\right)$

Answer

$\dfrac{1}{p^3 q^3}$

Try It $\PageIndex{27}$

Simplify:$\left(r^{5} s^{-3}\right)\left(r^{-7} s^{-5}\right)$

Answer

$\dfrac{1}{r^2 s^8}$

If the monomials have numerical coefficients, we multiply the coefficients, just like we did earlier.

Example $\PageIndex{28}$

Simplify: $\left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right)$

Solution

$\begin{array}{ll}& \left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right) \\ \text { Rewrite with the like bases together. }& 2(-5) \cdot\left(x^{-6} x^{5}\right) \cdot\left(y^{8} y^{-3}\right)\\ \text { Multiply the coefficients and add the exponents of each variable. }&-10 \cdot x^{-1} \cdot y^{5}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&-10 \cdot \dfrac{1}{x^{1}} \cdot y^{5} \\ \text { Simplify. } & \dfrac{-10 y^{5}}{x}\end{array}$

Try It $\PageIndex{29}$

Simplify: $\left(3 u^{-5} v^{7}\right)\left(-4 u^{4} v^{-2}\right)$

Answer

$-\dfrac{12v^5}{u}$

Try It $\PageIndex{30}$

Simplify: $\left(-6 c^{-6} d^{4}\right)\left(-5 c^{-2} d^{-1}\right)$

Answer

$\dfrac{30d^3}{c^8}$

In the next two examples, we’ll use the Power Property and the Product to a Power Property.

Example $\PageIndex{31}$

Simplify: $\left(6 k^{3}\right)^{-2}$

Solution

$\begin{array}{ll}&\left(6 k^{3}\right)^{-2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&(6)^{-2}\left(k^{3}\right)^{-2}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&6^{-2} k^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{6^{2}} \cdot \dfrac{1}{k^{6}} \\ \text { Simplify. } & \dfrac{1}{36 k^{6}}\end{array}$

Try It $\PageIndex{32}$

Simplify: $\left(-4 x^{4}\right)^{-2}$

Answer

$\dfrac{1}{16x^8}$

Try It $\PageIndex{33}$

Simplify: $\left(2 b^{3}\right)^{-4}$

Answer

$\dfrac{1}{16b^{12}}$

Example $\PageIndex{34}$

Simplify: $\left(5 x^{-3}\right)^{2}$

Solution

$\begin{array}{ll}&\left(5 x^{-3}\right)^{2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&5^{2}\left(x^{-3}\right)^{2}\\ \begin{array}{l}{\text { Simplify } 5^{2} \text { and multiply the exponents of } x \text { using the Power }} \\ {\text { Property, }\left(a^{m}\right)^{n}=a^{m \cdot n} .}\end{array}&25 \cdot x^{-6}\\ \begin{array}{l}{\text { Rewrite } x^{-6} \text { by using the Definition of a Negative Exponent, }} \\ {\space a^{-n}=\dfrac{1}{a^{n}}}\end{array}&25 \cdot \dfrac{1}{x^{6}}\\ \text { Simplify. } & \dfrac{25}{x^{6}}\end{array}$

Try It $\PageIndex{35}$

Simplify: $\left(8 a^{-4}\right)^{2}$

Answer

$\dfrac{64}{a^8}$

Try It $\PageIndex{36}$

Simplify: $\left(2 c^{-4}\right)^{3}$

Answer

$\dfrac{8}{c^{12}}$

To simplify a fraction, we use the Quotient Property and subtract the exponents.

Example $\PageIndex{37}$

Simplify: $\dfrac{r^{5}}{r^{-4}}$

Solution

$\begin{array}{l} & \dfrac{r^{5}}{r^{-4}}\\ {\text { Use the Quotient Property, } \dfrac{a^{n}}{a^{n}}=a^{m-n}} & r^{5-(-4)}\\ {\text { Simplify. }} & r^{9}\end{array}$

Try It $\PageIndex{38}$

Simplify: $\dfrac{x^{8}}{x^{-3}}$

Answer

$x^{11}$

Try It $\PageIndex{39}$

Simplify: $\dfrac{y^{8}}{y^{-6}}$

Answer

$y^{14}$

Convert from Decimal Notation to Scientific Notation

Remember working with place value for whole numbers and decimals? Our number system is based on powers of 10. We use tens, hundreds, thousands, and so on. Our decimal numbers are also based on powers of tens—tenths, hundredths, thousandths, and so on. Consider the numbers 4,000 and 0.004. We know that 4,000 means $4 \times 1,000$ and 0.004 means $4 \times \dfrac{1}{1,000}$.

If we write the 1000 as a power of ten in exponential form, we can rewrite these numbers in this way:

$$\begin{array}{ll}{4,000} & {0.004} \\ {4 \times 1,000} & {4 \times \dfrac{1}{1,000}} \\ {4 \times 10^{3}} & {4 \times \dfrac{1}{10^{3}}} \\ & {4 \times 10^{-3}}\end{array}$$

When a number is written as a product of two numbers, where the first factor is a number greater than or equal to one but less than 10, and the second factor is a power of 10 written in exponential form, it is said to be in scientific notation.

SCIENTIFIC NOTATION

A number is expressed in scientific notation when it is of the form

$$a \times 10^{n} \text { where } 1 \leq a<10 \text { and } n \text { is an integer }$$

It is customary in scientific notation to use as the $\times$ multiplication sign, even though we avoid using this sign elsewhere in algebra.

If we look at what happened to the decimal point, we can see a method to easily convert from decimal notation to scientific notation.

In both cases, the decimal was moved 3 places to get the first factor between 1 and 10.

$\begin{array}{ll}{\text { The power of } 10 \text { is positive when the number is larger than } 1 :} & {4,000=4 \times 10^{3}} \\ {\text { The power of } 10 \text { is negative when the number is between } 0 \text { and } 1 :} & {0.004=4 \times 10^{-3}} \end{array}$

Example $\PageIndex{40}$: HOW TO CONVERT FROM DECIMAL NOTATION TO SCIENTIFIC NOTATION

Write in scientific notation: 37000.

Solution

Try It $\PageIndex{41}$

Write in scientific notation: 96000.

Answer

$9.6 \times 10^{4}$

Try It $\PageIndex{42}$

Write in scientific notation: 48300.

Answer

$4.83 \times 10^{4}$

HOW TO: Convert from decimal notation to scientific notation

1. Step 1. Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
2. Step 2. Count the number of decimal places, n, that the decimal point was moved.
3. Step 3. Write the number as a product with a power of 10.
   If the original number is:
   • greater than 1, the power of 10 will be 10ⁿ.
   • between 0 and 1, the power of 10 will be 10⁻ⁿ.
4. Step 4. Check.

Example $\PageIndex{43}$

Write in scientific notation: 0.0052.

Solution

The original number, 0.0052, is between 0 and 1 so we will have a negative power of 10.

Move the decimal point to get 5.2, a number between 1 and 10.
Count the number of decimal places the point was moved.
Write as a product with a power of 10.
Check.
$\begin{array}{l}{5.2 \times 10^{-3}} \\ {5.2 \times \dfrac{1}{10^{3}}} \\ {5.2 \times \dfrac{1}{1000}} \\ {5.2 \times 0.001}\end{array}$
0.0052

Try It $\PageIndex{44}$

Write in scientific notation: 0.0078

Answer

$7.8 \times 10^{-3}$

Try It $\PageIndex{45}$

Write in scientific notation: 0.0129

Answer

$1.29 \times 10^{-2}$

Convert Scientific Notation to Decimal Form

How can we convert from scientific notation to decimal form? Let’s look at two numbers written in scientific notation and see.

$$\begin{array}{cc}{9.12 \times 10^{4}} & {9.12 \times 10^{-4}} \\ {9.12 \times 10,000} & {9.12 \times 0.0001} \\ {91,200} & {0.000912}\end{array}$$

If we look at the location of the decimal point, we can see an easy method to convert a number from scientific notation to decimal form.

$$9.12 \times 10^{4}=91,200 \quad 9.12 \times 10^{-4}=0.000912$$

In both cases the decimal point moved 4 places. When the exponent was positive, the decimal moved to the right. When the exponent was negative, the decimal point moved to the left.

Example $\PageIndex{46}$

Convert to decimal form: $6.2 \times 10^{3}$

Solution

Try It $\PageIndex{47}$

Convert to decimal form: $1.3 \times 10^{3}$

Answer

$1,300$

Try It $\PageIndex{48}$

Convert to decimal form: $9.25 \times 10^{4}$

Answer

$92,500$

The steps are summarized below.

HOW TO

Convert scientific notation to decimal form.

To convert scientific notation to decimal form:

1. Step 1. Determine the exponent, $n$, on the factor $10$.
2. Step 2. Move the decimal $n$ places, adding zeros if needed.
   • If the exponent is positive, move the decimal point $n$ places to the right.
   • If the exponent is negative, move the decimal point $|n|$ places to the left.
3. Step 3. Check.

Example $\PageIndex{49}$

Convert to decimal form: $8.9\times 10^{-2}$

Solution

Determine the exponent, $n$, on the factor $10$.
Since the exponent is negative, move the decimal point 2 places to the left.
Add zeros as needed for placeholders.

Try It $\PageIndex{50}$

Convert to decimal form: $1.2 \times 10^{-4}$

Answer

$0.00012$

Try It $\PageIndex{51}$

Convert to decimal form: $7.5 \times 10^{-2}$

Answer

$0.075$

Multiply and Divide Using Scientific Notation

Astronomers use very large numbers to describe distances in the universe and ages of stars and planets. Chemists use very small numbers to describe the size of an atom or the charge on an electron. When scientists perform calculations with very large or very small numbers, they use scientific notation. Scientific notation provides a way for the calculations to be done without writing a lot of zeros. We will see how the Properties of Exponents are used to multiply and divide numbers in scientific notation.

Example $\PageIndex{52}$

Multiply. Write answers in decimal form:$\left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)$

Solution

$\begin{array}{ll} & \left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\\\text { Use the Commutative Property to rearrange the factors. }& 4 \cdot 2 \cdot 10^{5} \cdot 10^{-7} \\ \text{ Multiply.} & 8 \times 10^{-2} \\ \text { Change to decimal form by moving the decimal two places left. } & 0.08\end{array}$

Try It $\PageIndex{53}$

Multiply $(3\times 10^{6})(2\times 10^{-8})$. Write answers in decimal form.

Answer

$0.06$

Try It $\PageIndex{54}$

Multiply $\left(3 \times 10^{-2}\right)\left(3 \times 10^{-1}\right)$. Write answers in decimal form.

Answer

$0.009$

Example $\PageIndex{55}$

Divide. Write answers in decimal form: $\dfrac{9 \times 10^{3}}{3 \times 10^{-2}}$

Solution

$\begin{array}{ll} & \dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\\\text { Separate the factors, rewriting as the product of two fractions. }& \dfrac{9}{3} \times \dfrac{10^{3}}{10^{-2}}\\ \text{ Divide.} & 3 \times 10^{5} \\ \text { Change to decimal form by moving the decimal five places right. } & 300000\end{array}$

Try It $\PageIndex{56}$

Divide $\dfrac{8 \times 10^{4}}{2 \times 10^{-1}} .$ Write answers in decimal form.

Answer

$400,000$

Try It $\PageIndex{57}$

Divide $\dfrac{8 \times 10^{2}}{4 \times 10^{-2}} .$ Write answers in decimal form.

Answer

$20,000$

MEDIA ACCESS ADDITIONAL ONLINE RESOURCES

Access these online resources for additional instruction and practice with integer exponents and scientific notation:

• Negative Exponents
• Scientific Notation
• Scientific Notation 2

Key Concepts

• Property of Negative Exponents
  • If $n$ is a positive integer and $a \ne 0$, then $\dfrac{1}{a^{−n}}=a^n$
• Quotient to a Negative Exponent
  • If $a$ and $b$ are real numbers, $b \ne 0$ and $n$ is an integer , then $\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n$
• To convert scientific notation to decimal form:
  1. Determine the exponent, $n$ on the factor $10$.
  2. Move the decimal $n$ places, adding zeros if needed.
     • If the exponent is positive, move the decimal point $n$ places to the right.
     • If the exponent is negative, move the decimal point $|n|$ places to the left.
  3. Check.
• To convert a decimal to scientific notation:
  1. Move the decimal point so that the first factor is greater than or equal to $1$ but less than $10$.
  2. Count the number of decimal places, $n$ that the decimal point was moved.
  3. Write the number as a product with a power of $10$. If the original number is:
     • greater than $1$, the power of $10$ will be $10^n$
     • between $0$ and $1$, the power of $10$ will be $10^{−n}$
  4. Check.

Glossary

negative exponent

If $n$ is a positive integer and $a \neq 0$, then $a^{-n}=\dfrac{1}{a^{n}}$.

scientific notation

A number is expressed in scientific notation when it is of the form $a \times 10^{n}$ where $a \geq 1$ and a<10 and $n$ is an integer.