8.5E: Exercises
- Page ID
- 30270
Practice Makes Perfect
Simplify a Complex Rational Expression by Writing It as Division
In the following exercises, simplify.
\(\frac{\frac{2a}{a+4}}{\frac{4a^2}{a^2−16}}\)
- Answer
-
\(\frac{a−4}{2a}\)
\(\frac{\frac{3b}{b−5}}{\frac{b^2}{b^2−25}}\)
\(\frac{\frac{5}{c^2+5c−14}}{\frac{10}{c+7}}\)
- Answer
-
\(\frac{1}{2(c−2)}\)
\(\frac{\frac{8}{d^2+9d+18}}{\frac{12}{d+6}}\)
\(\frac{\frac{1}{2}+\frac{5}{6}}{\frac{2}{3}+\frac{7}{9}}\)
- Answer
-
\(\frac{24}{26}\)
\(\frac{\frac{1}{2}+\frac{3}{4}}{\frac{3}{5}+\frac{7}{10}}\)
\(\frac{\frac{2}{3}−\frac{1}{9}}{\frac{3}{4}+\frac{5}{6}}\)
- Answer
-
\(\frac{20}{57}\)
\(\frac{\frac{1}{2}−\frac{1}{6}}{\frac{2}{3}+\frac{3}{4}}\)
\(\frac{\frac{n}{m}+\frac{1}{n}}{\frac{1}{n}−\frac{n}{m}}\)
- Answer
-
\(\frac{n^2+m}{m−n^2}\)
\(\frac{\frac{1}{p}+\frac{p}{q}}{\frac{q}{p}−\frac{1}{q}}\)
\(\frac{\frac{1}{r}+\frac{1}{t}}{\frac{1}{r^2}−\frac{1}{t^2}}\)
- Answer
-
\(\frac{rt}{t−r}\)
\(\frac{\frac{2}{v}+\frac{2}{w}}{\frac{1}{v^2}−\frac{1}{w^2}}\)
\(\frac{x−\frac{2x}{x+3}}{\frac{1}{x+3}+\frac{1}{x−3}}\)
- Answer
-
\(\frac{(x+1)(x−3)}{2}\)
\(\frac{y−\frac{2y}{y−4}}{\frac{2}{y−4}−\frac{2}{y+4}}\)
\(\frac{2−\frac{2}{a+3}}{\frac{1}{a+3}+\frac{a}{2}}\)
- Answer
-
\(\frac{4}{a+1}\)
\(\frac{4−\frac{4}{b−5}}{\frac{1}{b−5}+\frac{b}{4}}\)
In the following exercises, simplify.
\(\frac{\frac{1}{3}+\frac{1}{8}}{\frac{1}{4}+\frac{1}{12}}\)
- Answer
-
\(\frac{1}{18}\)
\(\frac{\frac{1}{4}+\frac{1}{9}}{\frac{1}{6}+\frac{1}{12}}\)
\(\frac{\frac{5}{6}+\frac{2}{9}}{\frac{7}{18}−\frac{1}{3}}\)
- Answer
-
19
\(\frac{\frac{1}{6}+\frac{4}{15}}{\frac{3}{5}−\frac{1}{2}}\)
\(\frac{\frac{c}{d}+\frac{1}{d}}{\frac{1}{d}−\frac{d}{c}}\)
- Answer
-
\(\frac{c^2+c}{c−d^2}\)
\(\frac{\frac{1}{m}+\frac{m}{n}}{\frac{n}{m}−\frac{1}{n}}\)
\(\frac{\frac{1}{p}+\frac{1}{q}}{\frac{1}{p^2}−\frac{1}{q^2}}\)
- Answer
-
\(\frac{pq}{q−p}\)
\(\frac{\frac{2}{r}+\frac{2}{t}}{\frac{1}{r^2}−\frac{1}{t^2}}\)
\(\frac{\frac{2}{x+5}}{\frac{3}{x−5}+\frac{1}{x^2−25}}\)
- Answer
-
\(\frac{2x−10}{3x+16}\)
\(\frac{\frac{5}{y−4}}{\frac{3}{y+4}+\frac{2}{y^2−16}}\)
\(\frac{\frac{5}{z^2−64}+\frac{3}{z+8}}{\frac{1}{z+8}+\frac{2}{z−8}}\)
- Answer
-
\(\frac{3z−19}{3z+8}\)
\(\frac{\frac{3}{s+6}+\frac{5}{s−6}}{\frac{1}{s^2−36}+\frac{4}{s+6}}\)
\(\frac{\frac{4}{a^2−2a−15}}{\frac{1}{a−5}+\frac{2}{a+3}}\)
- Answer
-
\(\frac{4}{3a−2}\)
\(\frac{\frac{5}{b^2−6b−27}}{\frac{3}{b−9}+\frac{1}{b+3}}\)
\(\frac{\frac{5}{c+2}−\frac{3}{c+7}}{\frac{5c}{c^2+9c+14}}\)
- Answer
-
\(\frac{2c+29}{5c}\)
\(\frac{\frac{6}{d−4}−\frac{2}{d+7}}{\frac{2d}{d^2+3d−28}}\)
\(\frac{2+\frac{1}{p−3}}{\frac{5}{p−3}}\)
- Answer
-
\(\frac{(2p−5)}{5}\)
\(\frac{\frac{n}{n−2}}{3+\frac{5}{n−2}}\)
\(\frac{\frac{m}{m+5}}{4+\frac{1}{m−5}}\)
- Answer
-
\(\frac{m(m−5)}{4m^2+m−95}\)
\(\frac{7+\frac{2}{q−2}}{\frac{1}{q+2}}\)
In the following exercises, use either method.
\(\frac{\frac{3}{4}−\frac{2}{7}}{\frac{1}{2}+\frac{5}{14}}\)
- Answer
-
\(\frac{13}{24}\)
\(\frac{\frac{v}{w}+\frac{1}{v}}{\frac{1}{v}−\frac{v}{w}}\)
\(\frac{\frac{2}{a+4}}{\frac{1}{a^2−16}}\)
- Answer
-
2(a−4)
\(\frac{\frac{3}{b^2−3b−40}}{\frac{5}{b+5}−\frac{2}{b−8}}\)
\(\frac{\frac{3}{m}+\frac{3}{n}}{\frac{1}{m^2}−\frac{1}{n^2}}\)
- Answer
-
\(\frac{3mn}{n−m}\)
\(\frac{\frac{2}{r−9}}{\frac{1}{r+9}+\frac{3}{r^2−81}}\)
\(\frac{x−\frac{3x}{x+2}}{\frac{3}{x+2}+\frac{3}{x−2}}\)
- Answer
-
\(\frac{(x−1)(x−2)}{6}\)
\(\frac{\frac{y}{y+3}}{2+\frac{1}{y−3}}\)
Everyday Math
Electronics The resistance of a circuit formed by connecting two resistors in parallel is \(\frac{1}{\frac{1}{R1}+\frac{1}{R2}}\)
- Simplify the complex fraction \(\frac{1}{\frac{1}{R1}+\frac{1}{R2}}\)
- Find the resistance of the circuit when R1=8 and R2=12
- Answer
-
- \(\frac{R1R2}{R2+R1}\)
- \(\frac{24}{5}\)
Ironing Lenore can do the ironing for her family’s business in hh hours. Her daughter would take h+2 hours to get the ironing done. If Lenore and her daughter work together, using 2 irons, the number of hours it would take them to do all the ironing is \(\frac{1}{\frac{1}{h}+\frac{1}{h+2}}\)
- Simplify the complex fraction \(\frac{1}{\frac{1}{h}+\frac{1}{h+2}}\)
- Find the number of hours it would take Lenore and her daughter, working together, to get the ironing done if h=4
Writing Exercises
In this section, you learned to simplify the complex fraction \(\frac{\frac{3}{x+2}}{\frac{x}{x^2−4}}\) two ways:
rewriting it as a division problem
multiplying the numerator and denominator by the LCD
Which method do you prefer? Why?
- Answer
-
Answers will vary.
Efraim wants to start simplifying the complex fraction \(\frac{\frac{1}{a}+\frac{1}{b}}{\frac{1}{a}−\frac{1}{b}}\) by cancelling the variables from the numerator and denominator. Explain what is wrong with Efraim’s plan.
Self Check
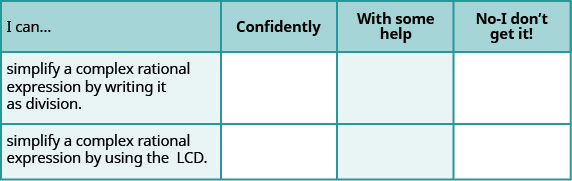
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
ⓑ After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?