9.1E: Exercises

Practice Makes Perfect

Simplify Expressions with Square Roots

In the following exercises, simplify.

Example $\PageIndex{34}$

$\sqrt{36}$

Answer

6

Example $\PageIndex{35}$

$\sqrt{4}$

Example $\PageIndex{36}$

$\sqrt{64}$

Answer

8

Example $\PageIndex{37}$

$\sqrt{169}$

Example $\PageIndex{38}$

$\sqrt{9}$

Answer

3

Example $\PageIndex{39}$

$\sqrt{16}$​​​​​​​

Example $\PageIndex{40}$

$\sqrt{100}$

Answer

10​​​​​​​

Example $\PageIndex{41}$

$\sqrt{144}$​​​​​​​

Example $\PageIndex{42}$

$−\sqrt{4}$

Answer

−2​​​​​​​

Example $\PageIndex{43}$

$−\sqrt{100}$​​​​​​​

Example $\PageIndex{44}$

$−\sqrt{1}$

Answer

−1​​​​​​​

Example $\PageIndex{45}$

$−\sqrt{121}$​​​​​​​

Example $\PageIndex{46}$

$\sqrt{−121}$

Answer

not a real number

Example $\PageIndex{47}$

$\sqrt{−36}$

Example $\PageIndex{48}$

$\sqrt{−9}$

Answer

not a real number​​​​​​​

Example $\PageIndex{49}$

$\sqrt{−49}$​​​​​​​

Example $\PageIndex{50}$

$\sqrt{9+16}$

Answer

5​​​​​​​

Example $\PageIndex{51}$

$\sqrt{25+144}$​​​​​​​

Example $\PageIndex{52}$

$\sqrt{9}+\sqrt{16}$

Answer

7​​​​​​​

Example $\PageIndex{53}$

$\sqrt{25}+\sqrt{144}$

​​​​​​​Estimate Square Roots

In the following exercises, estimate each square root between two consecutive whole numbers.

Example $\PageIndex{54}$

$\sqrt{70}$

Answer

$8<\sqrt{70}<9$​​​​​​​

Example $\PageIndex{55}$

$\sqrt{55}$​​​​​​​

Example $\PageIndex{56}$

$\sqrt{200}$

Answer

$14<\sqrt{200}<15$

Example $\PageIndex{57}$

$\sqrt{172}$

​​​​​​​Approximate Square Roots

In the following exercises, approximate each square root and round to two decimal places.

Example $\PageIndex{58}$

$\sqrt{19}$

Answer

4.36​​​​​​​

Example $\PageIndex{59}$

$\sqrt{21}$​​​​​​​

Example $\PageIndex{60}$

$\sqrt{53}$

Answer

7.28​​​​​​​

Example $\PageIndex{61}$

$\sqrt{47}$

​​​​​​​Simplify Variable Expressions with Square Roots

In the following exercises, simplify.

Example $\PageIndex{62}$

$\sqrt{y^2}$

Answer

y​​​​​​​

Example $\PageIndex{63}$

$\sqrt{b^2}$​​​​​​​

Example $\PageIndex{64}$

$\sqrt{a^{14}}$

Answer

$a^7$​​​​​​​

Example $\PageIndex{65}$

$\sqrt{w^{24}}$​​​​​​​

Example $\PageIndex{66}$

$\sqrt{49x^2}$

Answer

$7x$​​​​​​​

Example $\PageIndex{67}$

$\sqrt{100y^2}$​​​​​​​

Example $\PageIndex{68}$

$\sqrt{121m^{20}}$

Answer

$11m^{10}$​​​​​​​

Example $\PageIndex{69}$

$25h^{44}$​​​​​​​

Example $\PageIndex{70}$

$\sqrt{81x^{36}}$

Answer

$9x^{18}$​​​​​​​

Example $\PageIndex{71}$

$\sqrt{144z^{84}}$​​​​​​​

Example $\PageIndex{72}$

$−\sqrt{81x^{18}}$

Answer

$−9x^9$​​​​​​​

Example $\PageIndex{73}$

$−\sqrt{100m^{32}}$​​​​​​​

Example $\PageIndex{74}$

$−\sqrt{64a^2}$

Answer

$−8a$​​​​​​​

Example $\PageIndex{75}$

$−\sqrt{25x^2}$

Example $\PageIndex{76}$

$\sqrt{144x^{2}y^{2}}$

Answer

$12xy$

Example $\PageIndex{77}$

$\sqrt{196a^{2}b^{2}}$

Example $\PageIndex{78}$

$\sqrt{169w^{8}y^{10}}$

Answer

$13w^{4}y^{5}$

Example $\PageIndex{79}$

$\sqrt{81p^{24}q^{6}}$

Example $\PageIndex{80}$

$\sqrt{9c^{8}d^{12}}$

Answer

$3c^{4}d^{6}$

Examlpe $\PageIndex{81}$

$\sqrt{36r^{6}s^{20}}$

Everyday Math

Example $\PageIndex{82}$

Decorating Denise wants to have a square accent of designer tiles in her new shower. She can afford to buy 625 square centimeters of the designer tiles. How long can a side of the accent be?

Answer

25 centimeters

Example $\PageIndex{83}$

Decorating Morris wants to have a square mosaic inlaid in his new patio. His budget allows for 2025 square inch tiles. How long can a side of the mosaic be?​​​​​​​

Writing Exercises

Example $\PageIndex{84}$

Why is there no real number equal to $\sqrt{−64}$?

Answer

Answers will vary.

Example $\PageIndex{85}$

What is the difference between $9^{2}$ and $\sqrt{9}$?

Self Check

ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

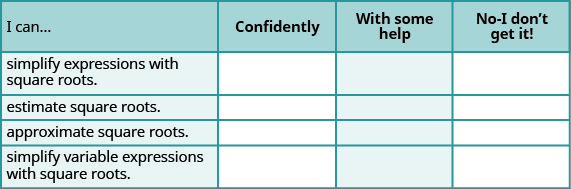
ⓑ On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?