Chapter 10 Review Exercises
- Page ID
- 30584
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Chapter 10 Review Exercises
10.1 Solve Quadratic Equations Using the Square Root Property
In the following exercises, solve using the Square Root Property.
\(x^2=100\)
- Answer
-
\(x=\pm10\)
\(y^2=144\)
\(m^2−40=0\)
- Answer
-
\(m=\pm2\sqrt{10}\)
\(n^2−80=0\)
\(4a^2=100\)
- Answer
-
\(a=\pm5\)
\(2b^2=72\)
\(r^2+32=0\)
- Answer
-
no solution
\(t^2+18=0\)
\(\frac{4}{3}v^2+4=28\)
- Answer
-
\(v=\pm3\sqrt{2}\)
\(\frac{2}{3}w^2−20=30\)
\(5c^2+3=19\)
- Answer
-
\(c=\pm\frac{4\sqrt{5}}{5}\)
\(3d^2−6=43\)
In the following exercises, solve using the Square Root Property.
\((p−5)^2+3=19\)
- Answer
-
p=1, 9
\((q+4)^2=9\)
\((u+1)^2=45\)
- Answer
-
\(u=−1\pm3\sqrt{5}\)
\((z−5)^2=50\)
\((x−\frac{1}{4})^2=\frac{3}{16}\)
- Answer
-
\(x=\frac{1}{4}\pm\frac{\sqrt{3}}{4}\)
\((y−\frac{2}{3})^2=\frac{2}{9}\)
\((m−7)^2+6=30\)
- Answer
-
\(m=7\pm2\sqrt{6}\)
\((n−4)^2−50=150\)
\((5c+3)^2=−20\)
- Answer
-
no solution
\((4c−1)^2=−18\)
\(m^2−6m+9=48\)
- Answer
-
\(m=3\pm4\sqrt{3}\)
\(n^2+10n+25=12\)
\(64a^2+48a+9=81\)
- Answer
-
a=−32, 34
\(4b^2−28b+49=25\)
10.2 Solve Quadratic Equations Using Completing the Square
In the following exercises, complete the square to make a perfect square trinomial. Then write the result as a binomial squared.
\(x^2+22x\)
- Answer
-
\((x+11)^2\)
\(y^2+6y\)
\(m^2−8m\)
- Answer
-
\((m−4)^2\)
\(n^2−10n\)
\(a^2−3a\)
- Answer
-
\((a−\frac{3}{2})^2\)
\(b^2+13b\)
\(p^2+\frac{4}{5}p\)
- Answer
-
\((p+\frac{2}{5})^2\)
\(q^2−13q\)
In the following exercises, solve by completing the square.
\(c^2+20c=21\)
- Answer
-
c=1, −21
\(d^2+14d=−13\)
\(x^2−4x=32\)
- Answer
-
x=−4, 8
\(y^2−16y=36\)
\(r^2+6r=−100\)
- Answer
-
no solution
\(t^2−12t=−40\)
\(v^2−14v=−31\)
- Answer
-
\(v=7\pm3\sqrt{2}\)
\(w^2−20w=100\)
\(m^2+10m−4=−13\)
- Answer
-
\(m=−9,−1\)
\(n^2−6n+11=34\)
\(a^2=3a+8\)
- Answer
-
\(a=\frac{3}{2}\pm\frac{\sqrt{41}}{2}\)
\(b^2=11b−5\)
\((u+8)(u+4)=14\)
- Answer
-
\(u=−6\pm2\sqrt{2}\)
\((z−10)(z+2)=28\)
\(3p^2−18p+15=15\)
- Answer
-
p=0, 6
\(5q^2+70q+20=0\)
\(4y^2−6y=4\)
- Answer
-
\(y=−\frac{1}{2}, 2\)
\(2x^2+2x=4\)
\(3c^2+2c=9\)
- Answer
-
\(c=−\frac{1}{3}\pm\frac{2\sqrt{7}}{3}\)
\(4d^2−2d=8\)
10.3 Solve Quadratic Equations Using the Quadratic Formula
In the following exercises, solve by using the Quadratic Formula.
\(4x^2−5x+1=0\)
- Answer
-
\(x=14, 1\)
\(7y^2+4y−3=0\)
\(r^2−r−42=0\)
- Answer
-
\(r=−6, 7\)
\(t^2+13t+22=0\)
\(4v^2+v−5=0\)
- Answer
-
\(v=−\frac{5}{4}, 1\)
\(2w^2+9w+2=0\)
\(3m^2+8m+2=0\)
- Answer
-
\(m=\frac{−4\pm\sqrt{10}}{3}\)
\(5n^2+2n−1=0\)
\(6a^2−5a+2=0\)
- Answer
-
no real solution
\(4b^2−b+8=0\)
\(u(u−10)+3=0\)
- Answer
-
\(u=5\pm2\sqrt{2}\)
\(5z(z−2)=3\)
\(\frac{1}{8}p^2−\frac{1}{5}p=−\frac{1}{20}\)
- Answer
-
\(p=\frac{4\pm\sqrt{6}}{5}\)
\(\frac{2}{5}q^2+\frac{3}{10}q=\frac{1}{10}\)
\(4c^2+4c+1=0\)
- Answer
-
\(c=−\frac{1}{2}\)
\(9d^2−12d=−4\)
In the following exercises, determine the number of solutions to each quadratic equation.
- \(9x^2−6x+1=0\)
- \(3y^2−8y+1=0\)
- \(7m^2+12m+4=0\)
- \(5n^2−n+1=0\)
- Answer
-
- 1
- 2
- 2
- none
- \(5x^2−7x−8=0\)
- \(7x^2−10x+5=0\)
- \(25x^2−90x+81=0\)
- \(15x^2−8x+4=0\)
In the following exercises, identify the most appropriate method (Factoring, Square Root, or Quadratic Formula) to use to solve each quadratic equation.
- \(16r^2−8r+1=0\)
- \(5t^2−8t+3=9\)\(3(c+2)^2=15\)
- Answer
-
- factor
- Quadratic Formula
- square root
- \(4d^2+10d−5=21\)
- \(25x^2−60x+36=0\)
- \(6(5v−7)^2=150\)
10.4 Solve Applications Modeled by Quadratic Equations
In the following exercises, solve by using methods of factoring, the square root principle, or the quadratic formula.
Find two consecutive odd numbers whose product is 323.
- Answer
-
Two consecutive odd numbers whose product is 323 are 17 and 19, and −17 and −19.
Find two consecutive even numbers whose product is 624.
A triangular banner has an area of 351 square centimeters. The length of the base is two centimeters longer than four times the height. Find the height and length of the base.
- Answer
-
The height of the banner is 13 cm and the length of the side is 54 cm.
Julius built a triangular display case for his coin collection. The height of the display case is six inches less than twice the width of the base. The area of the of the back of the case is 70 square inches. Find the height and width of the case.
A tile mosaic in the shape of a right triangle is used as the corner of a rectangular pathway. The hypotenuse of the mosaic is 5 feet. One side of the mosaic is twice as long as the other side. What are the lengths of the sides? Round to the nearest tenth.

- Answer
-
The lengths of the sides of the mosaic are 2.2 and 4.4 feet.
A rectangular piece of plywood has a diagonal which measures two feet more than the width. The length of the plywood is twice the width. What is the length of the plywood’s diagonal? Round to the nearest tenth.
The front walk from the street to Pam’s house has an area of 250 square feet. Its length is two less than four times its width. Find the length and width of the sidewalk. Round to the nearest tenth.
- Answer
-
The width of the front walk is 8.1 feet and its length is 30.8 feet.
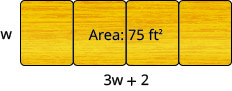
For Sophia’s graduation party, several tables of the same width will be arranged end to end to give a serving table with a total area of 75 square feet. The total length of the tables will be two more than three times the width. Find the length and width of the serving table so Sophia can purchase the correct size tablecloth. Round answer to the nearest tenth.
-
A ball is thrown vertically in the air with a velocity of 160 ft/sec. Use the formula \(h=−16t^2+v_{0}t\) to determine when the ball will be 384 feet from the ground. Round to the nearest tenth.
- Answer
-
The ball will reach 384 feet on its way up in 4 seconds and on the way down in 6 seconds.
A bullet is fired straight up from the ground at a velocity of 320 ft/sec. Use the formula \(h=−16t^2+v_{0}t\) to determine when the bullet will reach 800 feet. Round to the nearest tenth.
10.5 Graphing Quadratic Equations in Two Variables
In the following exercises, graph by plotting point.
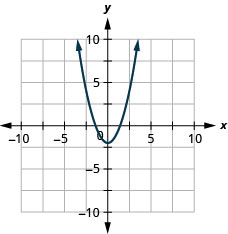
Graph \(y=x^2−2\)
- Answer
-
Graph \(y=−x^2+3\)
In the following exercises, determine if the following parabolas open up or down.
\(y=−3x^2+3x−1\)
- Answer
-
down
\(y=5x^2+6x+3\)
\(y=x^2+8x−1\)
- Answer
-
up
A\(y=−4x^2−7x+1\)
In the following exercises, find
- the axis of symmetry and,
- the vertex.
\(y=−x^2+6x+8\)
- Answer
-
- x=3
- (3,17)
\(y=2x^2−8x+1\)
In the following exercises, find the x- and y-intercepts.
\(y=x^2−4x+5\)
- Answer
-
y:(0,5); x:(5,0), (−1,0)
\(y=x^2−8x+15\)
\(y=x^2−4x+10\)
- Answer
-
y:(0,10); x:none
\(y=−5x^2−30x−46\)
\(y=16x^2−8x+1\)
- Answer
-
y:(0,1); x:(14,0)
\(y=x^2+16x+64\)
In the following exercises, graph by using intercepts, the vertex, and the axis of symmetry.
\(y=x^2+8x+15\)
- Answer
-
y:(0,15) ;x:(−3,0), (−5,0);
axis: x=−4; vertex:(−4,−1)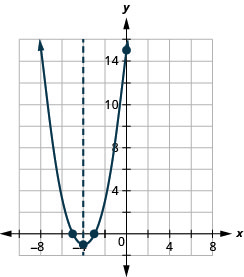
\(y=x^2−2x−3\)
\(y=−x^2+8x−16\)
- Answer
-
y:(0,−16); x:(4,0);
axis: x=4; vertex:(4,0)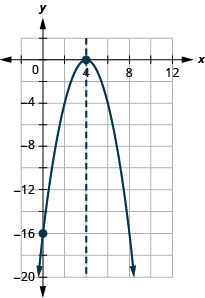
\(y=4x^2−4x+1\)
\(y=x^2+6x+13\)
- Answer
-
y:(0,13); x:none;
axis: x=−3; vertex:(−3,4)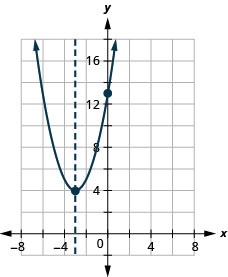
\(y=−2x^2−8x−12\)
\(y=−4x^2+16x−11\)
- Answer
-
y:(0,−11); x:(3.1,0),(0.9,0);
axis: x=2; vertex:(2,5)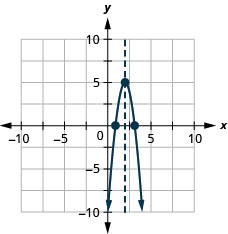
\(y=x^2+8x+10\)
In the following exercises, find the minimum or maximum value.
\(y=7x^2+14x+6\)
- Answer
-
The minimum value is −1 when \(x=−1\).
\(y=−3x^2+12x−10\)
In the following exercises, solve. Rounding answers to the nearest tenth.
A ball is thrown upward from the ground with an initial velocity of 112 ft/sec. Use the quadratic equation \(h=−16t^2+112t\) to find how long it will take the ball to reach maximum height, and then find the maximum height.
- Answer
-
In 3.5 seconds the ball is at its maximum height of 196 feet.
A daycare facility is enclosing a rectangular area along the side of their building for the children to play outdoors. They need to maximize the area using 180 feet of fencing on three sides of the yard. The quadratic equation \(A=−2x^2+180x\) gives the area, A, of the yard for the length, x, of the building that will border the yard. Find the length of the building that should border the yard to maximize the area, and then find the maximum area.
Practice Test
Use the Square Root Property to solve the quadratic equation: \(3(w+5)^2=27\).
- Answer
-
w=−2, −8
Use Completing the Square to solve the quadratic equation: \(a^2−8a+7=23\)
Use the Quadratic Formula to solve the quadratic equation: \(2m^2−5m+3=0\).
- Answer
-
m=1, 32
Solve the following quadratic equations. Use any method.
\(8v^2+3=35\)
\(3n^2+8n+3=0\)
- Answer
-
\(n=\frac{−4\pm\sqrt{7}}{3}\)
\(2b^2+6b−8=0\)
\(x(x+3)+12=0\)
- Answer
-
no real solution
\(\frac{4}{3}y^2−4y+3=0\)
Use the discriminant to determine the number of solutions of each quadratic equation.
\(6p^2−13p+7=0\)
- Answer
-
2
\(3q^2−10q+12=0\)
Solve by factoring, the Square Root Property, or the Quadratic Formula.
Find two consecutive even numbers whose product is 360.
- Answer
-
Two consecutive even number are −20 and −18 and 18 and 20.
The length of a diagonal of a rectangle is three more than the width. The length of the rectangle is three times the width. Find the length of the diagonal. (Round to the nearest tenth.)
For each parabola, find
- which ways it opens,
- the axis of symmetry,
- the vertex,
- the x- and y-intercepts, and
- the maximum or minimum value.
\(y=3x^2+6x+8\)
- Answer
-
- up
- \(x=−1\)
- (−1,5)
- y:(0,8);x:none; y:(0,8)
- minimum value of 5 when \(x=−1\).
\(y=x^2−4\)
\(y=x^2+10x+24\)
- Answer
-
- up
- \(x=−5\)
- (−5,−1)
- y:(0,24); x:(−6,0), (−4,0)
- minimum value of −5 when \(x=−1\)
\(y=−3x^2+12x−8\)
\(y=−x^2−8x+16\)
- Answer
-
- down
- \(x=−4\)
- (−4,32)
- y;(0,16); x:(−9.7,0),(1.7,0)
- maximum value of 32 when \(x=−4\)
Graph the following parabolas by using intercepts, the vertex, and the axis of symmetry.
\(y=2x^2+6x+2\)
\(y=16x^2+24x+9\)
- Answer
-
y:(0,9); x:(−34,0)
axis:\( x=−\frac{3}{4}\); vertex:\((−\frac{3}{4},0)\)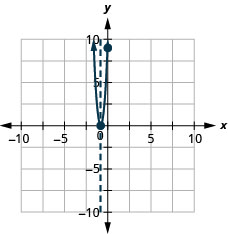
Solve.
A water balloon is launched upward at the rate of 86 ft/sec. Using the formula h=−16t^2+86t, find how long it will take the balloon to reach the maximum height and then find the maximum height. Round to the nearest tenth.


