6.1: Polynomial Functions
- Page ID
- 19713
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- We’ve seen in previous sections that a monomial is the product of a number and one or more variable factors, each raised to a positive integral power, as in \(-3 x^{2}\) or 4\(x^{3} y^{4}\).
- We’ve also seen that a binomial is the sum or difference of two monomial terms, as in \(3 x+5, x^{2}+4,\) or \(3 x y^{2}=2 x^{2} y\).
- We’ve also seen that a trinomial is the sum or difference of three monomial terms, as in \(x^{2}-2 x-3\) or \(x^{2}-4 x y+5 y^{2}\).
The root word “poly” means “many,” as in polygon (many sides) or polyglot (speaking many languages—multilingual).
- In algebra, the word polynomial means “many terms,” where the phrase “many terms” can be construed to mean anywhere from one to an arbitrary, but finite, number of terms. Consequently, a monomial could be considered a polynomial, as could binomials and trinomials. In our work, we will concentrate for the most part on polynomials of a single variable. What follows is a more formal definition of a polynomial in a single variable \(x\).
The function p, defined by
\[p(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n} \label{1} \]
is called a polynomial in \(x\).
There are several important points to be made about this definition.
- The polynomial in our definition in Equation \ref{1} is arranged in ascending powers of \(x\). We could just as easily arrange our polynomial in descending powers of \(x\), as in \[p(x)=a_{n} x^{n}+\cdots+a_{2} x^{2}+a_{1} x+a_{0} \nonumber \]
- The numbers \(a_{0}, a_{1}, a_{2}, \dots, a_{n}\) are called the coefficients of the polynomial p. − If all of the coefficients are integers, then we say that “\(p\) is a polynomial with integer coefficients.” − If all of the coefficients are rational numbers, then we say that “\(p\) is a polynomial with rational coefficients.” − If all of the coefficients are real numbers, then we say that “\(p\) is a polynomial with real coefficients.”
- The degree of the polynomial \(p\) is \(n\), the highest power of \(x\).
- The leading term of the polynomial \(p\) is the term with the highest power of \(x\). In the case of Equation \ref{2}, the leading term is an \(x^n\).
Let’s look at an example.
Consider the polynomial
\[p(x)=3-4 x^{2}+5 x^{3}-6 x\nonumber \]
Find the degree, the leading term, and make a statement about the coefficients of p by referencing the Note above to determine integer or rational coefficients.
Solution
First, put the polynomial terms in order. Whether you use ascending or descending powers of x makes no difference. Choose one or the other. In descending powers of x,
\[p(x)=5 x^{3}-4 x^{2}-6 x+3 \label{5} \]
but in ascending powers of \(x\),
\[p(x)=3-6 x-4 x^{2}+5 x^{3} \label{6} \]
In either case, Equation \ref{5} or Equation \ref{6}, the degree of the polynomial is 3. Also, in either case, the leading term of the polynomial is 5\(x^{3}\). Because all coefficients of this polynomial are integers, we say that “p is a polynomial with integer coefficients.” However, all the coefficients are also rational numbers, so we could say that p is a polynomial with rational coefficients. For that matter, all of the coefficients of p are real numbers, so we could also say that p is a polynomial with real coefficients.
Let’s look at another example.
Consider the polynomial
\[p(x)=3-\frac{4}{3} x+\frac{2}{5} x^{2}-9 x^{3}+12 x^{4}. \nonumber \]
Find the degree, the leading term, and make a statement about the coefficients of \(p\).
Solution
Fortunately, the polynomial p is already arranged in ascending powers of x. The degree of p is 4 and the leading term is 12\(x^{4}\). Not all of the coefficients are integers, so we cannot say that “p is a polynomial with integer coefficients.” However, all of the coefficients are rational numbers, so we can say that “p is a polynomial with rational coefficients.” Because all of the coefficients of p are real numbers, we could also say that “\(p\) is a polynomial with real coefficients.”
Consider the polynomial \[p(x)=3-\frac{4}{3} x+\sqrt{2} x^{2}-9 x^{3}+\pi x^{5} \nonumber \]. Find the degree, the leading term, and make a statement about the coefficients of p.
Solution
Fortunately, the polynomial p is already arranged in ascending powers of x. The degree of p is 5 and the leading term is \(\pi x^{5}\). Not all of the coefficients are integers, so we cannot say that “p is a polynomial with integer coefficients.” Not all of the coefficients are rational numbers, so we cannot say that “p is a polynomial with rational coefficients.” However, because all of the coefficients of p are real numbers, we can say that “p is a polynomial with real coefficients.”
The Graph of \(y=x^{n}\)
The primary goal in this section is to discuss the end-behavior of arbitrary polynomials. By “end-behavior,” we mean the behavior of the polynomial for very small values of x (like −1 000, −10 000, −100 000, etc.) or very large values of x (like 1 000, 10 000, 100 000, etc.). Before we can explore the end-behavior of arbitrary polynomials, we must first examine the end-behavior of some very basic monomials. Specifically, we need to investigate the end-behavior of the graphs of \(y=x^{n}\), where n = 1, 2, 3, . . ..
Let’s first examine the graph of \(y=x^{n}\), when n is even. The graphs are simple enough to draw, either by creating a table of points or by using your graphing calculator. In Figure \(\PageIndex{1}\)(a), (b), and (c), we’ve drawn the graphs of \(y=x^{2}, y=x^{4},\) and \(y=x^{6}\), respectively.
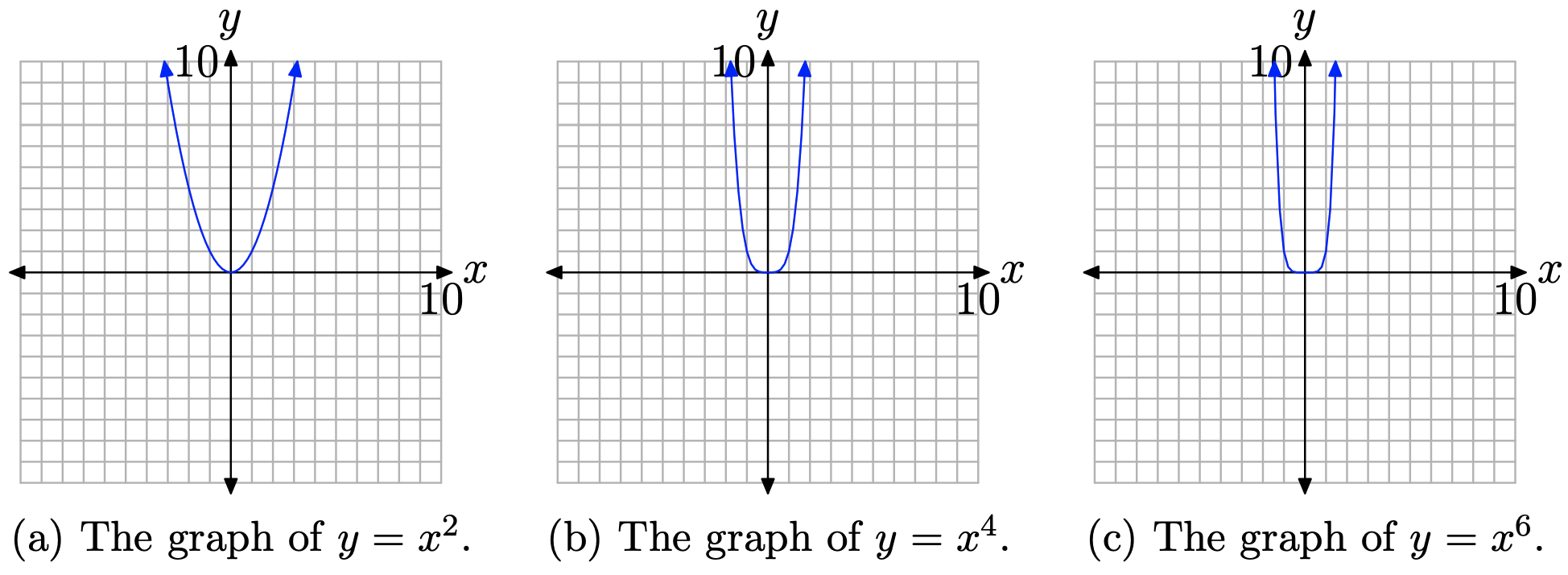
The graphs in Figure \(\PageIndex{1}\) share an important trait. As you sweep your eyes from left to right, each graph falls from positive infinity, wiggles through the origin, then rises back to positive infinity.
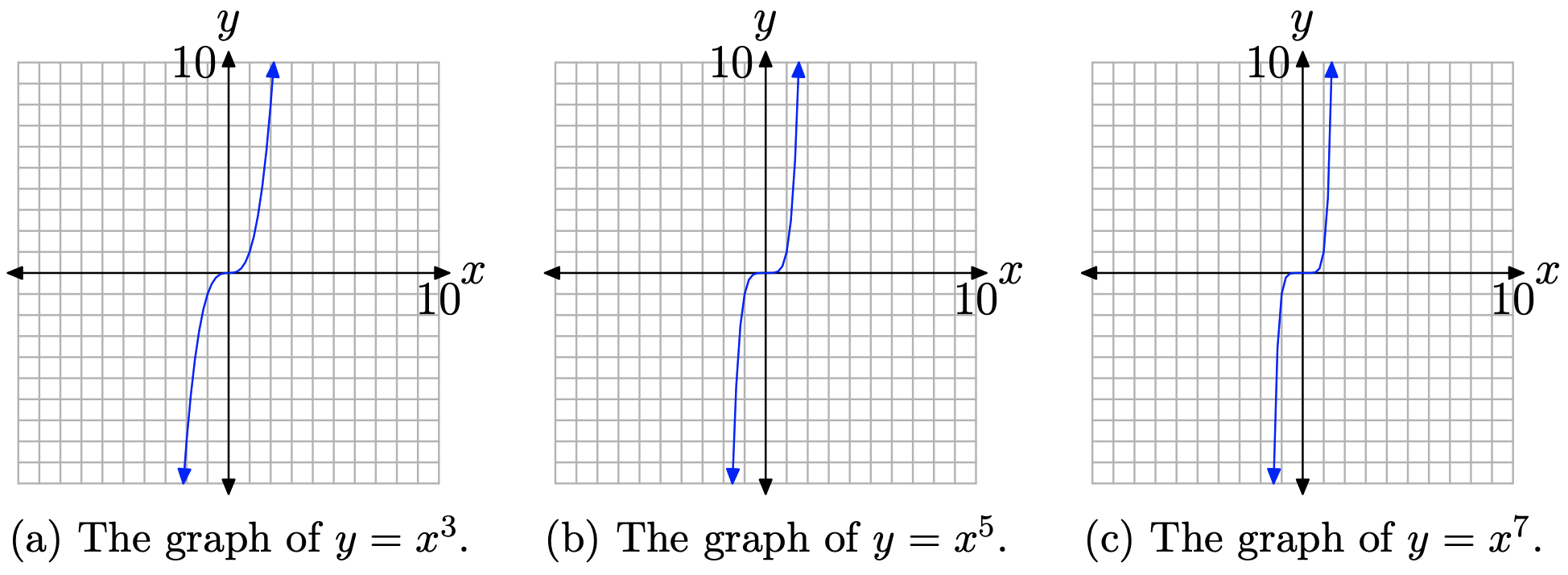
Next, let’s examine the graph of \(y=x^{n}\), when n is odd. Again, a table of points or a graphing calculator will help produce the graphs of \(y=x^{3}, y=x^{5},\) and \(y=x^{7}\), as shown in Figure \(\PageIndex{2}\)(a), (b), and (c), respectively.
The graphs in Figure \(\PageIndex{2}\) share an important trait. As you sweep your eyes from left to right, each graph rises from negative infinity, wiggles through the origin, then rises up to positive infinity.
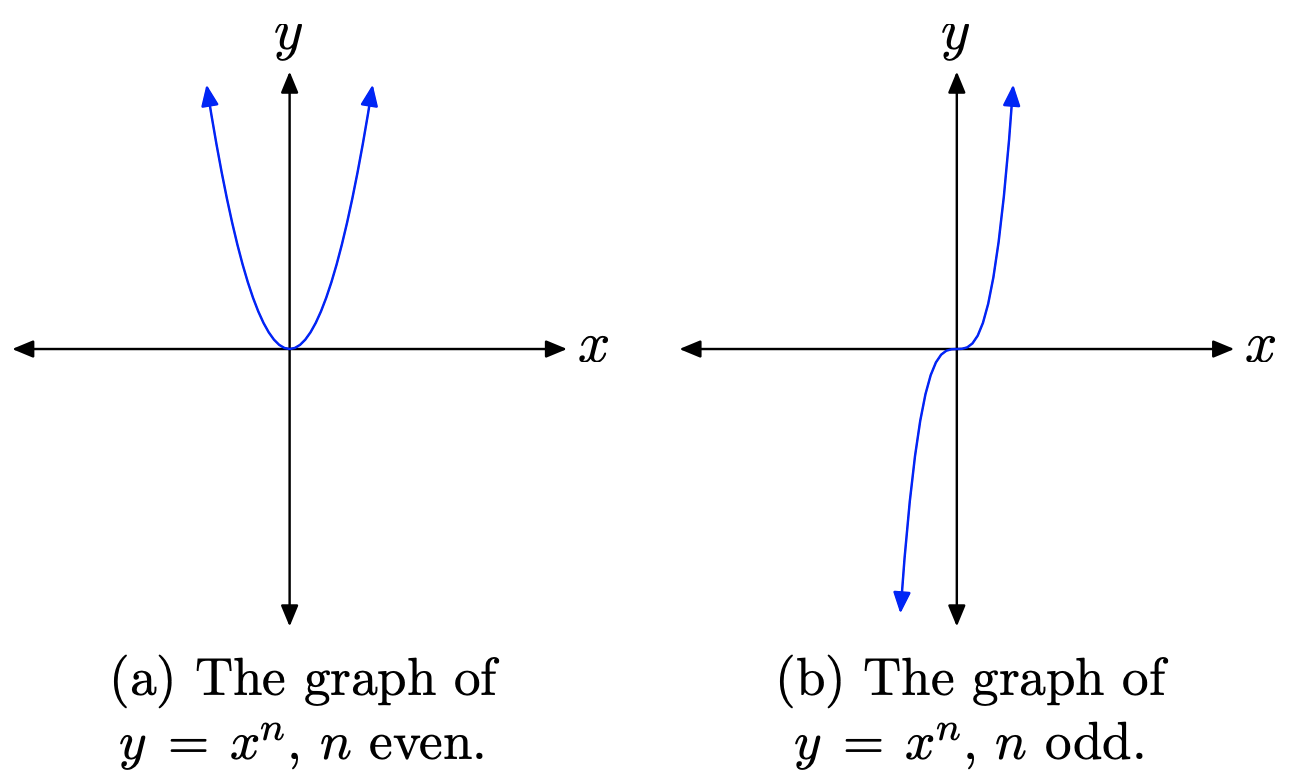
The behavior shown in Figure \(\PageIndex{1}\) and Figure \(\PageIndex{2}\) is typical.
When n is an even natural number, the graph of \(y=x^{n}\) will look like that shown in Figure \(\PageIndex{3}\)(a). If n is an odd natural number, then the graph of \(y=x^{n}\) will be similar to that shown in Figure \(\PageIndex{3}\)(b).
- When n is even, as you sweep your eyes from left to right, the graph of \(y=x^{n}\) falls from positive infinity, wiggles through the origin, then rises back to positive infinity.
- If n is odd, as you sweep your eyes from left to right, the graph of \(y=x^{n}\) rises from negative infinity, wiggles through the origin, then rises to positive infinity.
The Graph of \(y=a x^{n}\)
Now that we know the general shape of the graph of \(y=x^{n}\), let’s scale this function by multiplying by a constant, as in \(y=a x^{n}\).
In our study of the parabola, we learned that if we multiply by a factor of a, where a > 1, then we will stretch the graph in the vertical direction by a factor of a. Conversely, if we multiply the graph by a factor of a, where 0 < a < 1, then we will compress the graph in the vertical direction by a factor of 1/a. If a < 0, then not only will we scale the graph, but multiplying by this factor will also reflect the graph across the horizontal axis.
Let’s look at a few examples.
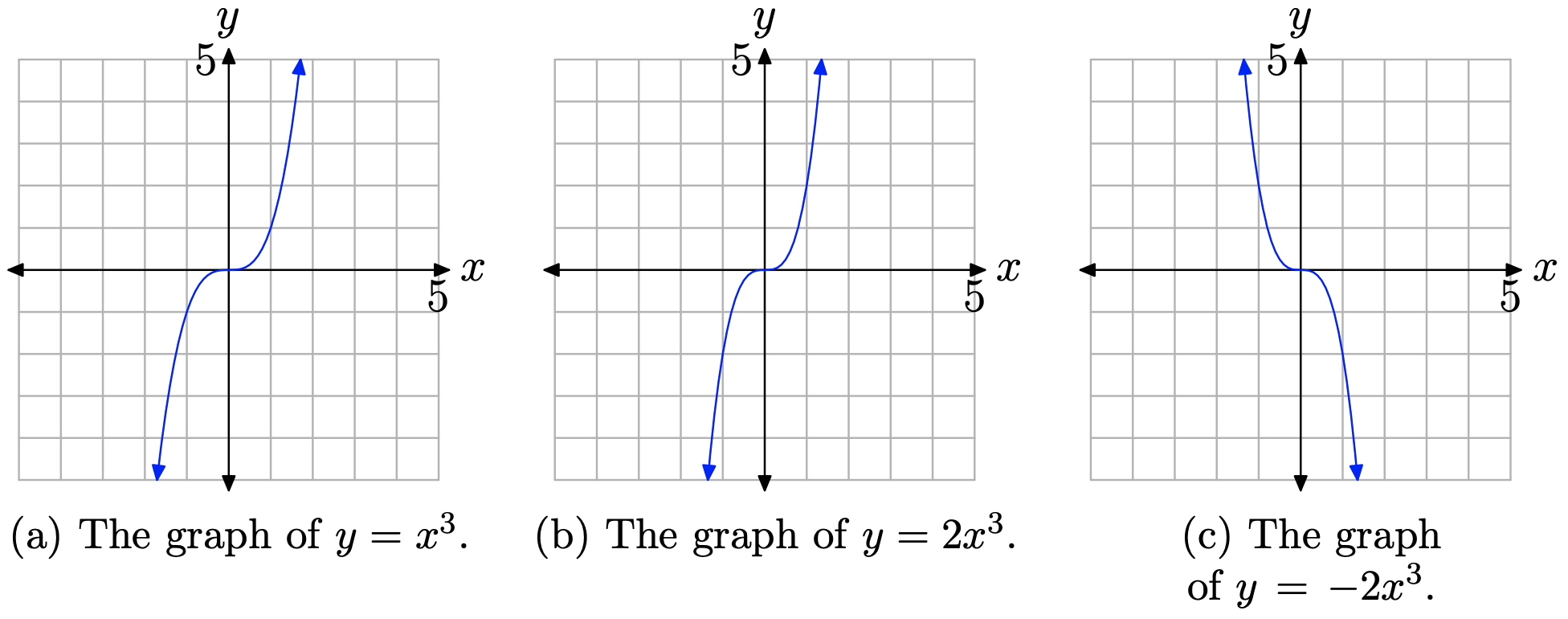
Sketch the graph of \(y=-2 x^{3}\).
Solution
We know what the graph of \(y=x^{3}\) looks like. As we sweep our eyes from left to right, the graph rises from negative infinity, wiggles through the origin, then rises to positive infinity. This behavior is shown in Figure \(\PageIndex{4}\)(a).
If we multiply by a factor of 2, then we stretch the original graph by a factor of 2 in the vertical direction. The graph of \(y=2 x^{3}\) is shown in Figure \(\PageIndex{4}\)(b). Note the stretching in the vertical direction.
Finally, if we negate by multiplying by −2, this will stretch the graph by a factor of 2, as in Figure \(\PageIndex{4}\)(b), but it will also reflect the graph across the x-axis. The graph of \(y=-2 x^{3}\) is shown in Figure \(\PageIndex{4}\)(c).
Let’s look at another example.
Sketch the graph of \(y=-\frac{1}{2} x^{4}\)
Solution
We know what the graph of \(y=x^{4}\) looks like. As we sweep our eyes from left to right, the graph falls from positive infinity, wiggles through the origin, then rises back to positive infinity. This behavior is shown in Figure \(\PageIndex{5}\)(a).
If we multiply by 1/2, then we will compress the graph by a factor of 2. Note that the graph of \(y=\frac{1}{2} x^{4}\) in Figure \(\PageIndex{5}\)(b) is compressed by a factor of 2 in the vertical direction.
Finally, if we multiply by −1/2, not only will we compress the graph by a factor of 2, we will also reflect the graph across the x-axis. The graph of \(y=-\frac{1}{2} x^{4}\) is shown in Figure \(\PageIndex{5}\)(c).
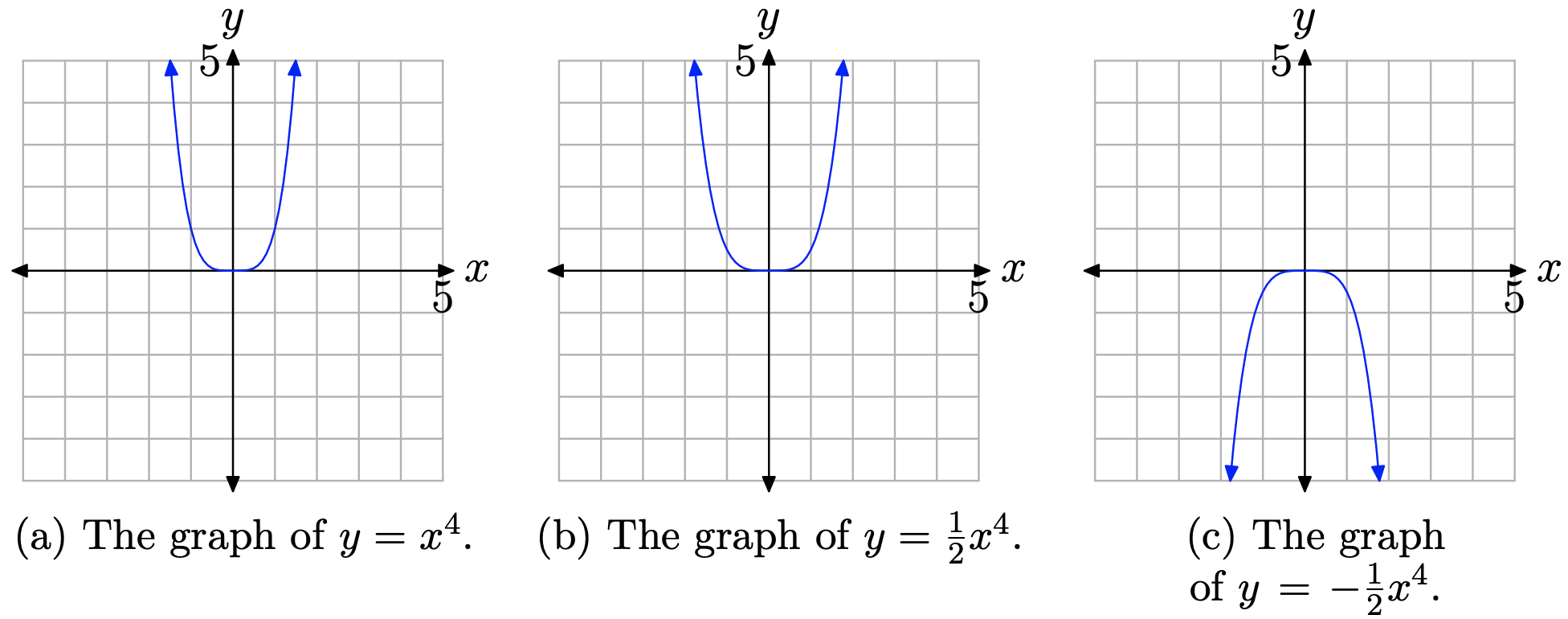
Hopefully, at this point you can now sketch the graph of \(y=a x^{n}\) for any real number a and any natural number n, either even or odd, without the use of a calculator. Let’s put this new-found knowledge to use in investigating the end-behavior of polynomials.
End Behavior
Consider the polynomial \[p(x)=x^{3}-7 x^{2}+7 x+15 \nonumber \] Here’s a key fact that we will use to determine the end-behavior of any polynomial.
A polynomial’s end-behavior is completely determined by its leading term. That is, the end-behavior of the graph of the polynomial will match the end-behavior of the graph of its leading term.
In a moment, we will show why this property is true. In the meantime, let’s accept the veracity of this statement and apply it to the polynomial defined by equation (12). The leading term of the polynomial \(p(x)=x^{3}-7 x^{2}+7 x+15\) is \(x^{3}\). We know the end behavior of graph of \(y=x^{3}\). As we sweep our eyes from left to right, the graph of \(y=x^{3}\) will rise from negative infinity, wiggle through the origin, then continue to rise to positive infinity. We pictured this behavior earlier in Figure \(\PageIndex{4}\)(a).
Property 13 tells us that the graph of the polynomial \(p(x)=x^{3}-7 x^{2}+7 x+15\) will exhibit the same end-behavior as the graph of its leading term, \(y=x^{3}\). We can predict that, as we sweep our eyes from left to right, the graph of the polynomial \(p(x)=x^{3}-7 x^{2}+7 x+15\) will rise from negative infinity, wiggle a bit, then rise to positive infinity. We don’t know what happens in-between, but we do know what happens at far left- and right-hand ends.
Our conjecture is verified by drawing the graph (use a graphing calculator). The graph of the polynomial \(p(x)=x^{3}-7 x^{2}+7 x+15\) is shown in Figure \(\PageIndex{6}\). Sure enough, as we sweep our eyes from left to right, the graph in Figure \(\PageIndex{6}\) rises from negative infinity as predicted, wiggles a bit, then continues its rise to positive infinity.
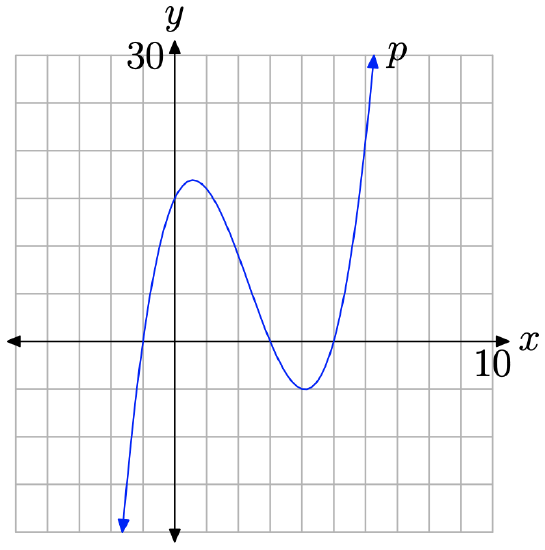
Why Does it Work? Why does Property 13 predict so accurately the end-behavior of this polynomial?
\[p(x)=x^{3}-7 x^{2}+7 x+15 \nonumber \]
We can demonstrate why by first factoring out the leading term.
\[p(x)=x^{3}\left(1-\frac{7}{x}+\frac{7}{x^{2}}+\frac{15}{x^{3}}\right) \nonumber \]
Now, ask the following question. What happens to the polynomial as we move to the right end? That is, what happens to the polynomial as we use large values of x, such as 1 000, 10 000, or even 100 000?
Consider the fraction 7/x. Because the numerator is fixed at 7, and the denominator is getting bigger and bigger (growing without bound), the fraction is getting closer and closer to zero. Calculus students would use the notation
\[\lim _{x \rightarrow \infty} \frac{7}{x}=0 \nonumber \]
Don’t be put off by the notation. We’re using sophisticated mathematical notation for a very simple idea that says “As x approaches infinity, the fraction 7/x approaches zero.”
Using similar reasoning, each of the fractions in equation (14) go to zero as x goes to infinity (increases without bound). Thus, as x gets larger and larger (as we move further and further to the right),
\[\lim _{x \rightarrow \infty} p(x)=\lim _{x \rightarrow \infty} x^{3}\left(1-\frac{7}{x}+\frac{7}{x^{2}}+\frac{15}{x^{3}}\right) \approx x^{3}(1-0+0+0+0) \approx x^{3} \nonumber \]
That is, as x increases without bound, the graph of \(p(x)=x^{3}-7 x^{2}+7 x+15\) should approximate the graph of \(y=x^{3}\).
Using similar reasoning, each of the fractions in equation (14) go to zero as x goes to minus infinity. That is, if you are putting in numbers for x such as −1 000, −10 000, −100 000, and the like, the fractions in equation (14) will go to zero. Hence, the polynomial p(x) must still approach its leading term x 3 for very small values of x (as x approaches \(-\infty\)).
If you superimpose the graph of \(y=x^{3}\) on the graph of \(p(x)=x^{3}-7 x^{2}+7 x+15\), as in Figure \(\PageIndex{7}\), it’s clear that the polynomial p has the same end-behavior as the graph of its leading term \(y=x^{3}\).
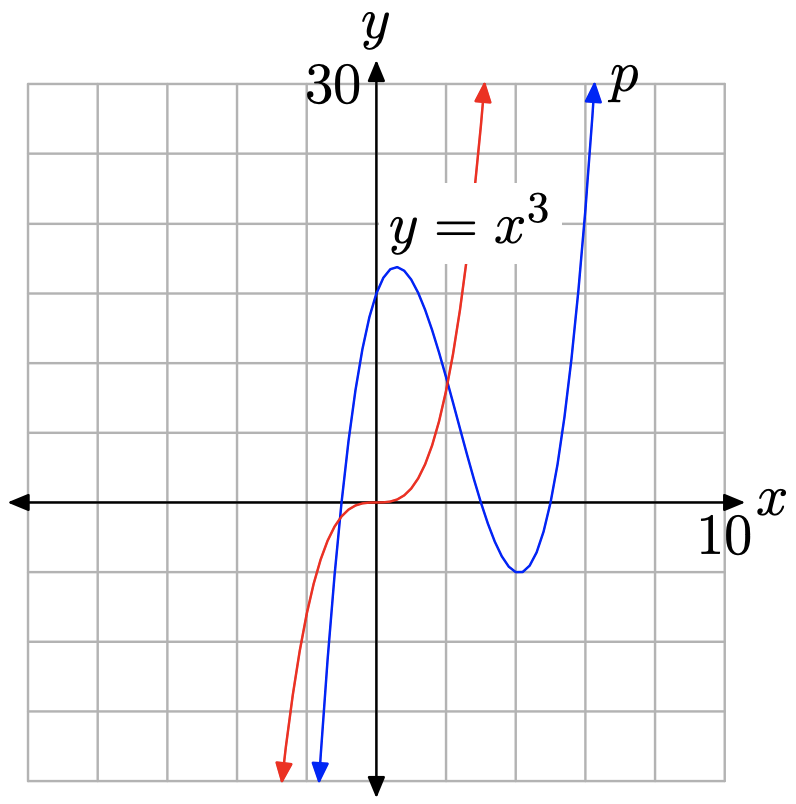
You can provide a more striking demonstration of the validity of the claim in equation (15) by plotting both the polynomial p and its leading term \(y=x^{3}\) on your calculator, then zooming out by adjusting the window parameters as shown in Figure \(\PageIndex{8}\)(b). Note how the graph of \(p(x)=x^{3}-7 x^{2}+7 x+15\) more closely resembles the graph of its leading term \(y=x^{3}\), at least at the right and left edges of the viewing window. When we zoom further out, by adjusting the window parameters as shown in Figure \(\PageIndex{8}\)(d), note how that graph of p approaches the graph of its leading term \(y=x^{3}\) even more closely at each edge of the viewing window.

Let’s look at another example.
Consider the polynomial \[p(x)=-x^{4}+37 x^{2}+24 x-180 \nonumber \]. Comment on the end-behavior of p and use your graphing calculator to sketch its graph.
Solution
The leading term of \(p(x)=-x^{4}+37 x^{2}+24 x-180\) is \(y=-x^{4}\). We know the end-behavior of the graph of the leading term. As we sweep our eyes from left to right, the graph of \(y=-x^{4}\) rises from negative infinity, wiggles through the origin, then falls back to minus infinity. The graph of p should exhibit the same end-behavior. Indeed, in Figure \(\PageIndex{9}\), note that the graph of \(y=-x^{4}\) and \(y=-x^{4}+37 x^{2}+24 x-180\) both share the same end-behavior.
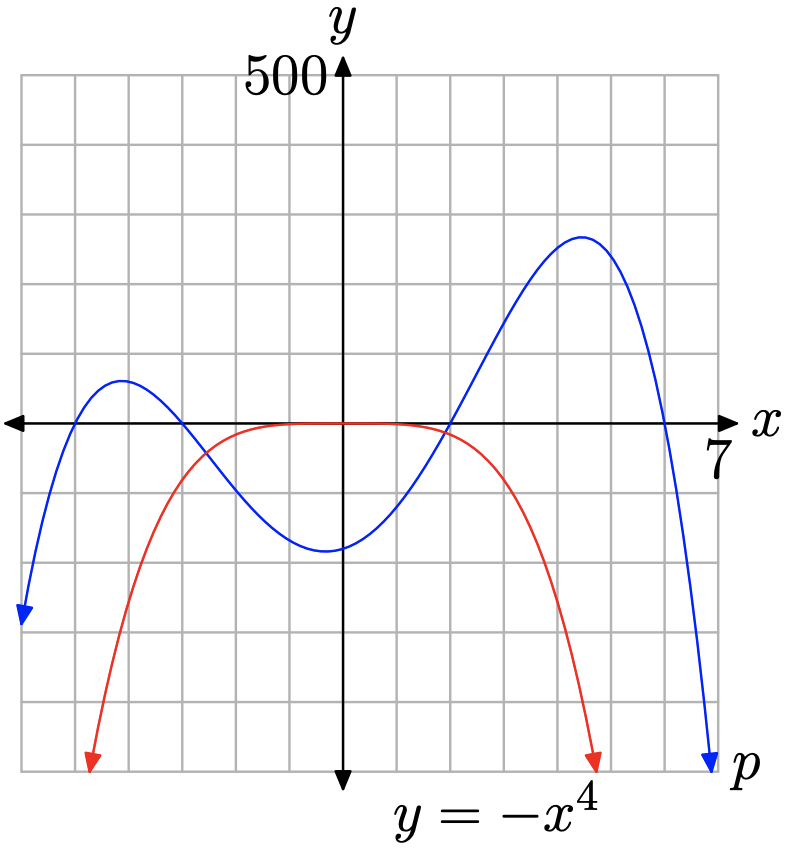
Exercise
In Exercises 1-8, arrange each polynomial in descending powers of x, state the degree of the polynomial, identify the leading term, then make a statement about the coefficients of the given polynomial by referencing the Note above Example \(\PageIndex{1}\) to determine integer or rational coefficients.
\(p(x) = 3x−x^2+4−x^3\)
- Answer
-
\(p(x) = −x^3−x^2+3x+4\), degree = 3, leading term = \(−x^3\), “p is a polynomial with integer coefficients, polynomial with rational coefficients,” or “p is
a polynomial with real coefficients.”
\(p(x) = 4+3x^2−5x+x^3\)
\(p(x) = 3x^2+x^4−x−4\)
- Answer
-
\(p(x) = x^4+3x^2−x−4\), degree = 4, leading term = \(x^4\), “p is a polynomial with integer coefficients,” “p is a polynomial with rational coefficients,” or “p is
a polynomial with real coefficients.”
\(p(x) = −3+x^2−x^3+5x^4\)
\(p(x) = 5x−\frac{3}{2}x^3+4−\frac{2}{3}x^5\)
- Answer
-
\(p(x) = −\frac{2}{3}x^5−\frac{3}{2}x^3+5x+4\), degree = 5, leading term = \(−\frac{2}{3}x^5\), “p is a polynomial with rational coefficients,” or p is a polynomial with real coefficients.”
\(p(x) = −\frac{3}{2}x+5−\frac{7}{3}x^5+\frac{4}{3}x^3\)
\(p(x) = −x+\frac{2}{3}x^3−\sqrt{2}x^2+\pi x^6\)
- Answer
-
\(p(x) = \pi x^6+\frac{2}{3}x^3−\sqrt{2}x^2−x\), degree = 6, leading term = \(\pi x^6\), “p is a polynomial with real coefficients.”
\(p(x) = 3+\sqrt{2}x^4+\sqrt{3}x−2x^2+\sqrt{5}x^6\)
In Exercises 9-14, you are presented with the graph of \(y = ax^{n}\). In each case, state whether the degree is even or odd, then state whether a is a positive or negative number.
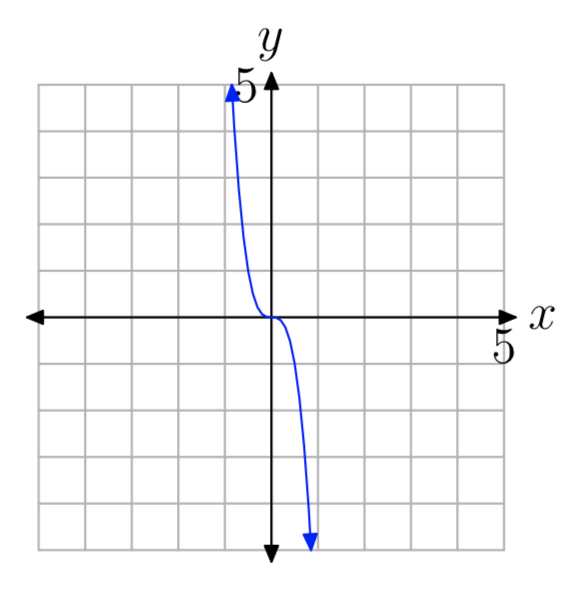
- Answer
-
\(y=ax^{n}\), n odd, a < 0.
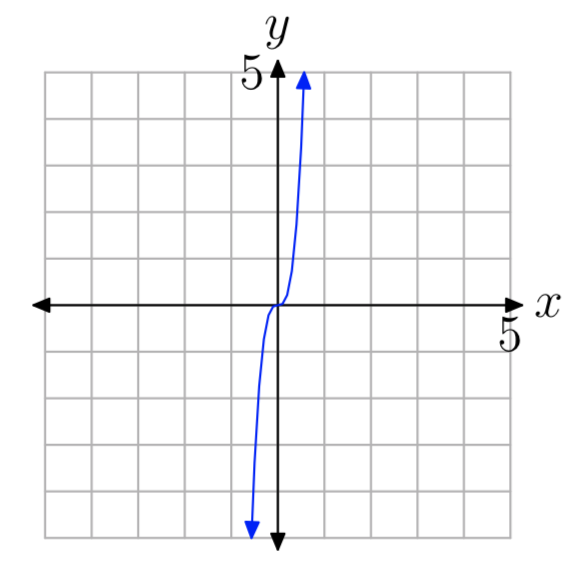
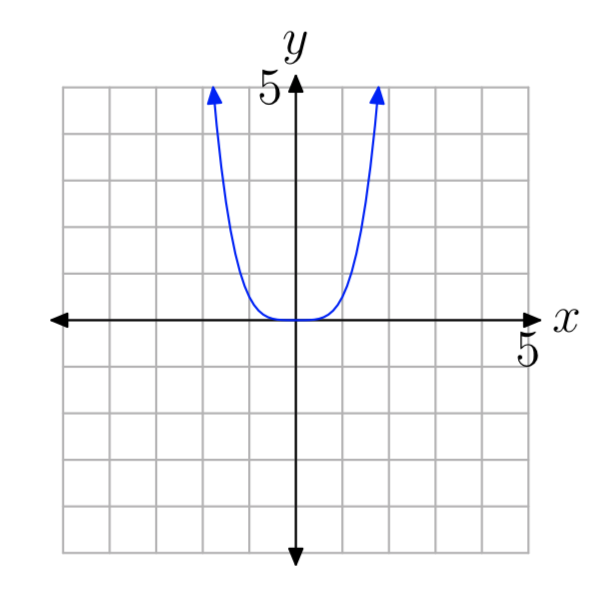
- Answer
-
\(y=ax^{n}\), n even, a > 0.
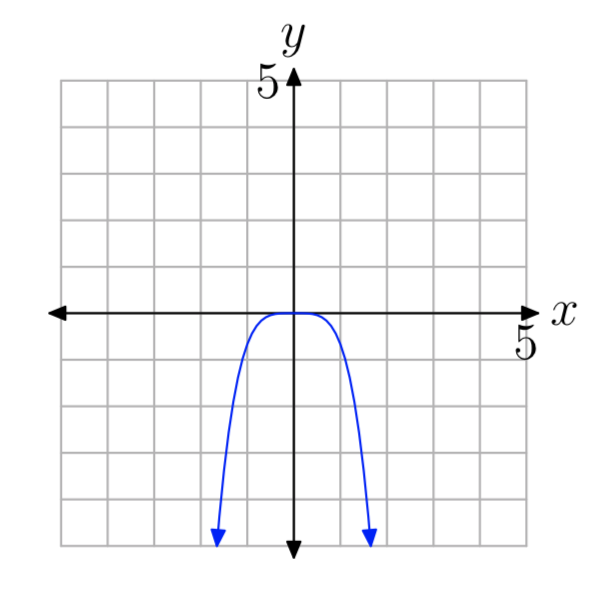
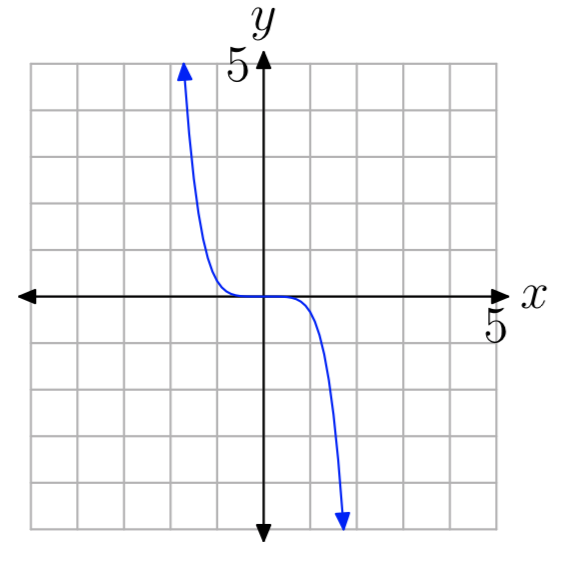
- Answer
-
\(y=ax^{n}\), n odd, a < 0.
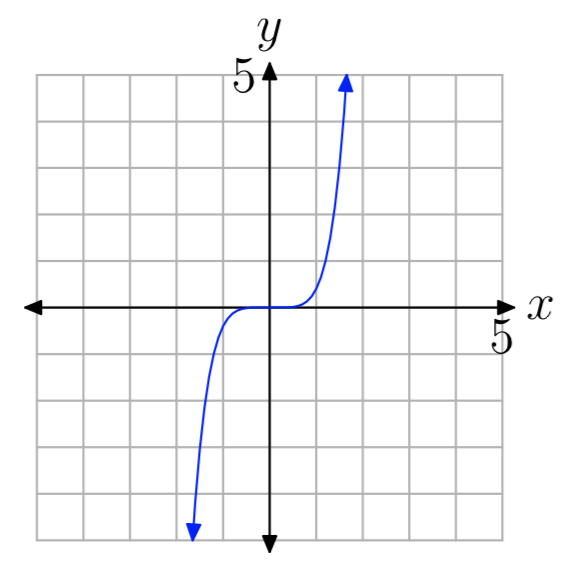
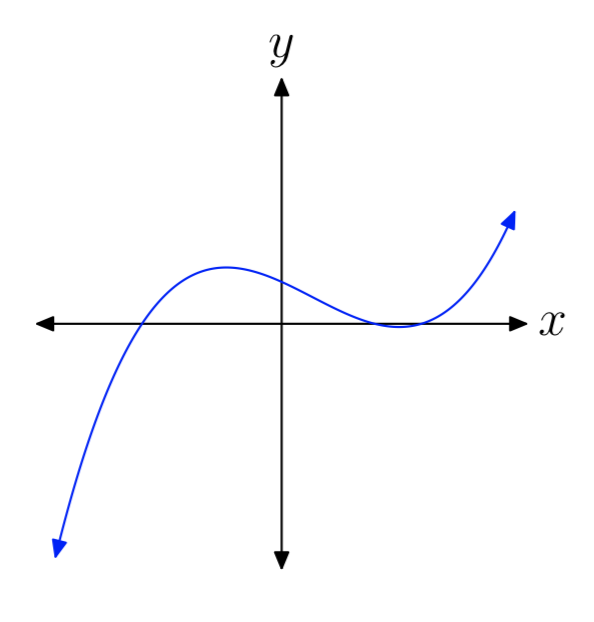
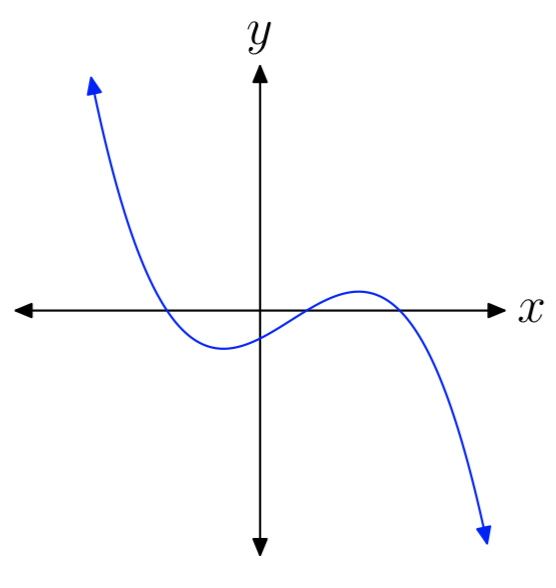
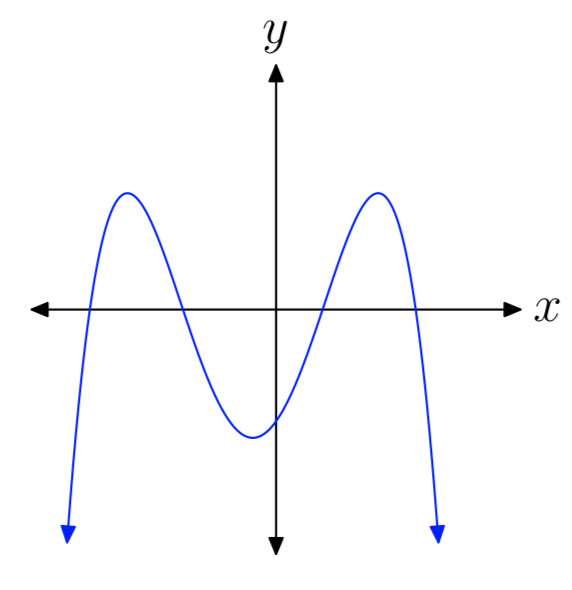
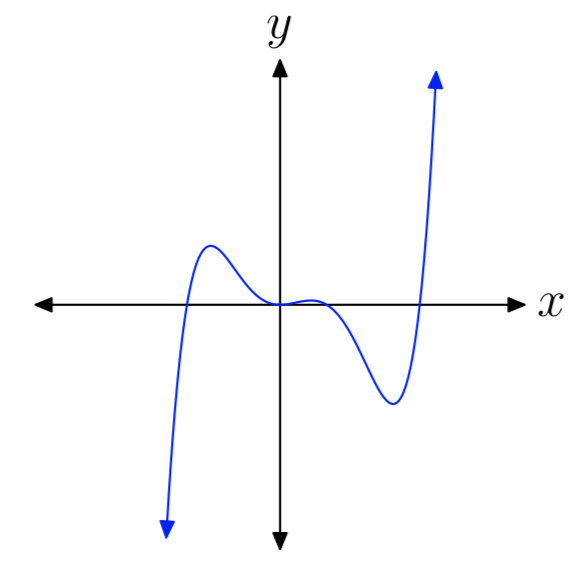
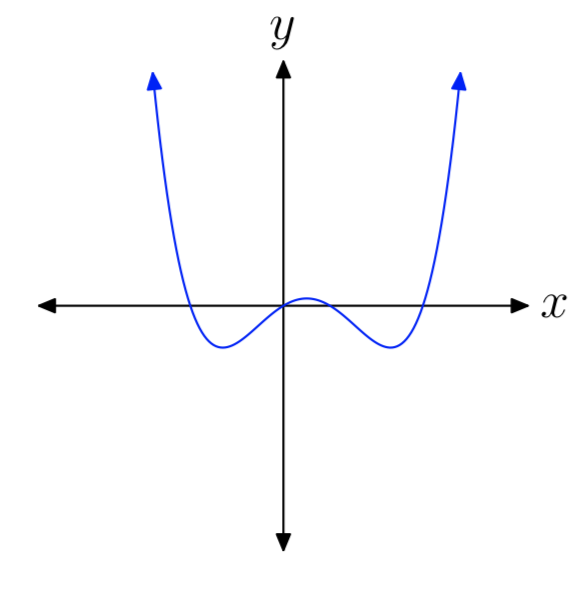
In Exercises 15-20, you are presented with the graph of the polynomial \(p(x) = a_{n}x^n +···+a_{1}x+a_{0}\). In each case, state whether the degree of the polynomial is even or odd, then state whether the leading coefficient an is positive or negative.
- Answer
-
odd, positive
- Answer
-
even, negative
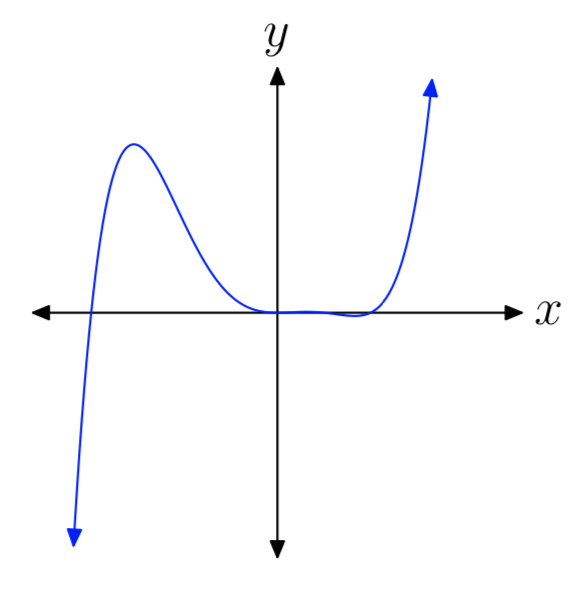
- Answer
-
odd, positive
For each polynomial in Exercises 21-30, perform each of the following tasks.
- Predict the end-behavior of the polynomial by drawing a very rough sketch of the polynomial. Do this without the assistance of a calculator. The only concern here is that your graph show the correct end-behavior.
- Draw the graph on your calculator, adjust the viewing window so that all “turning points” of the polynomial are visible in the viewing window, and copy the result onto your homework paper. As usual, label and scale each axis with xmin, xmax, ymin, and ymax. Does the actual end-behavior agree with your predicted end-behavior?
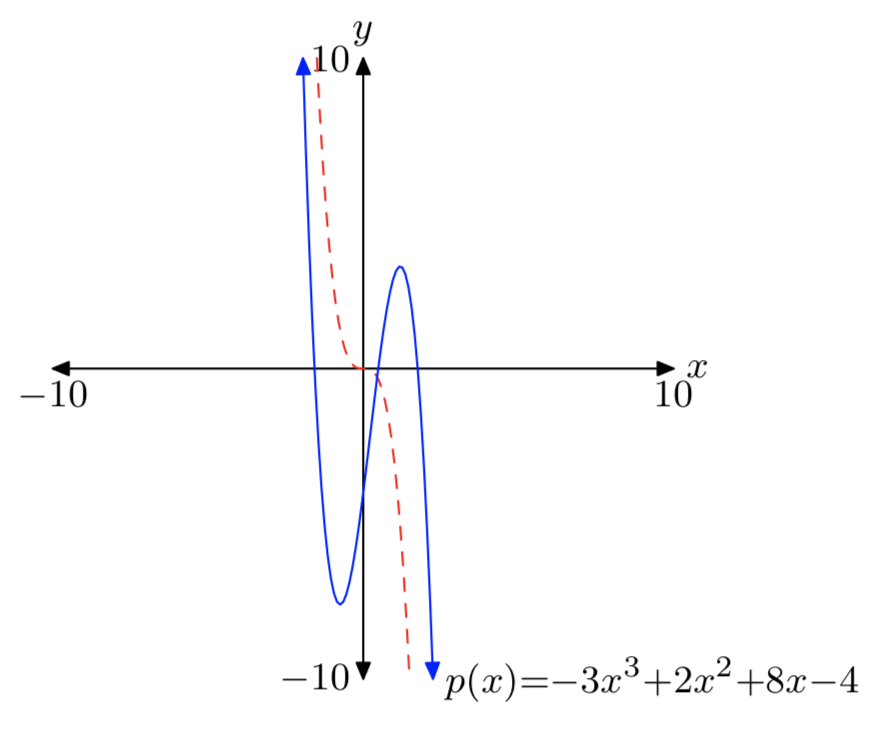
\(p(x) = −3x^3+2x^2+8x−4\)
- Answer
-
Note that the leading term \(−3x^3\) (dashed) has the same end-behavior as the polynomial p.
\(p(x) = 2x^3−3x^2+4x−8\)
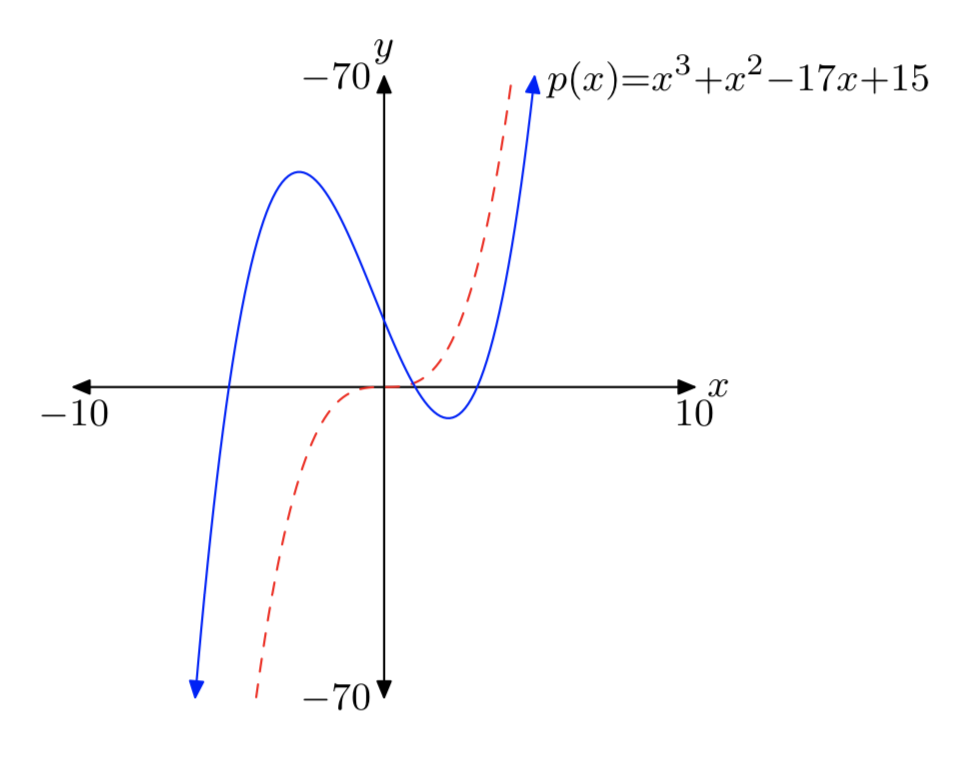
\(p(x) = x^3+x^2−17x+15\)
- Answer
-
Note that the leading term \(x^3\) (dashed) has the same end-behavior as the polynomial p.
\(p(x) = −x^4+2x^2+29x−30\)
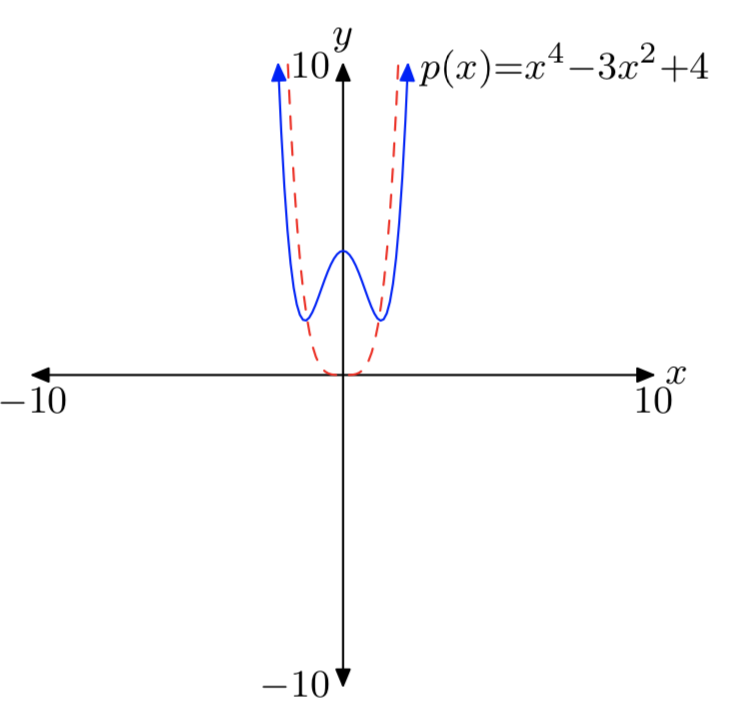
\(p(x) = x^4−3x^2+4\)
- Answer
-
Note that the leading term \(x^4\) (dashed) has the same end-behavior as the polynomial p.
\(p(x) = −x^4+8x^2−12\)
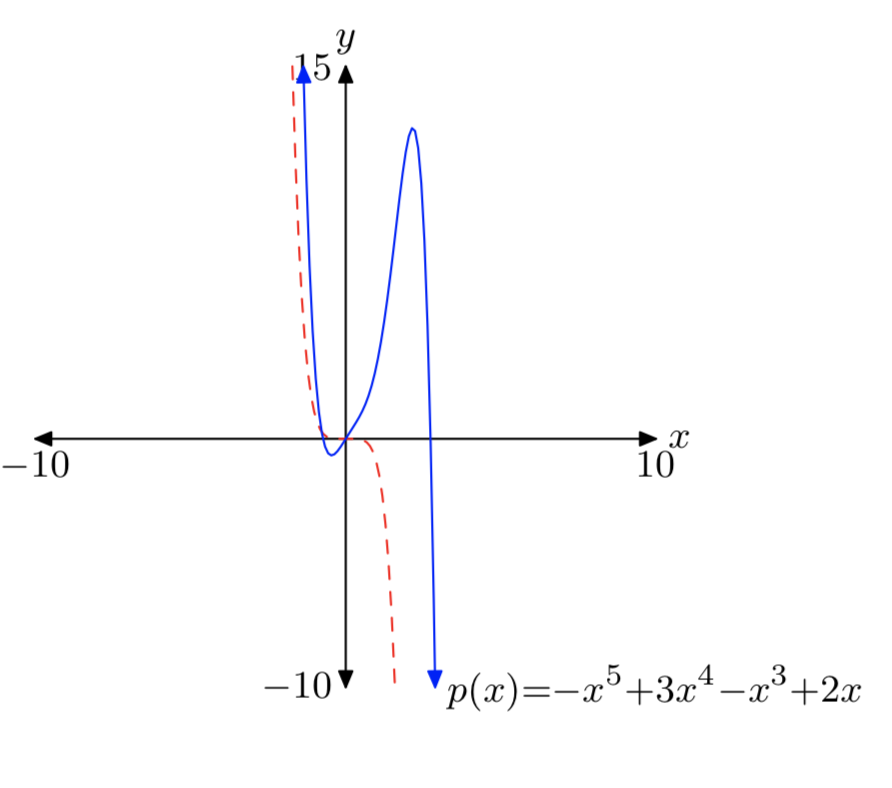
\(p(x) = −x^5+3x^4−x^3+2x\)
- Answer
-
Note that the leading term \(−x^5\) (dashed) has the same end-behavior as the polynomial p.
\(p(x) = 2x^4−3x^3+x−10\)
\(p(x) = −x^6−4x^5+27x^4+78x^3+4x^2+376x−480\)
- Answer
-
Note that the leading term \(−x^6\) (dashed) has the same end-behavior as the polynomial p.
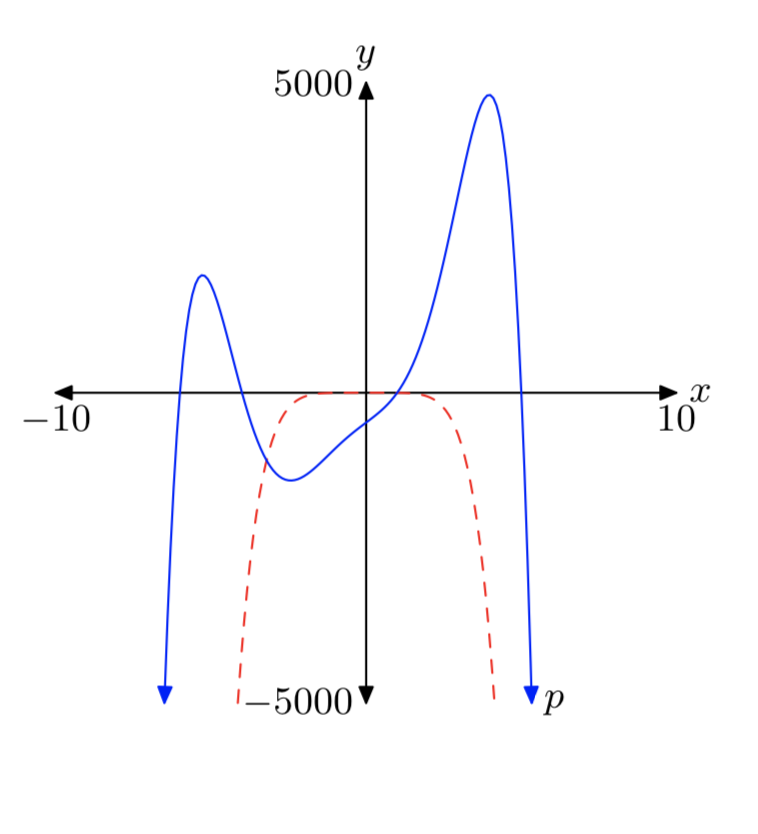
\(p(x) = x^5−27x^3+30x^2−124x+120\)


