9.6: The Pythagorean Theorem
- Page ID
- 19739
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Pythagoras was a Greek mathematician and philosopher, born on the island of Samos (ca. 582 BC). He founded a number of schools, one in particular in a town in southern Italy called Crotone, whose members eventually became known as the Pythagoreans. The inner circle at the school, the Mathematikoi, lived at the school, rid themselves of all personal possessions, were vegetarians, and observed a strict vow of silence. They studied mathematics, philosophy, and music, and held the belief that numbers constitute the true nature of things, giving numbers a mystical or even spiritual quality.
Today, nothing is known of Pythagoras’s writings, perhaps due to the secrecy and silence of the Pythagorean society. However, one of the most famous theorems in all of mathematics does bear his name, the Pythagorean Theorem.
Let c represent the length of the hypotenuse, the side of a right triangle directly opposite the right angle (a right angle measures 90º) of the triangle. The remaining sides of the right triangle are called the legs of the right triangle, whose lengths are designated by the letters a and b.
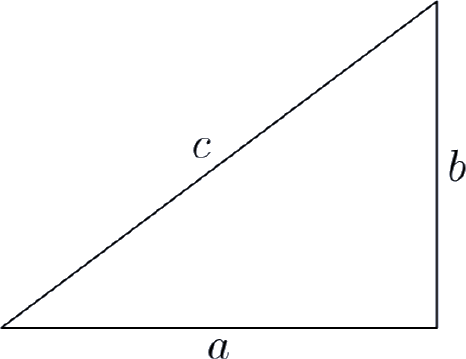
The relationship involving the legs and hypotenuse of the right triangle, given by
\[a^2 + b^2 = c^2 \label{1} \]
is called the Pythagorean Theorem.
Note that the Pythagorean Theorem can only be applied to right triangles. Let’s look at a simple application of the Pythagorean Theorem (Equation \ref{1}).
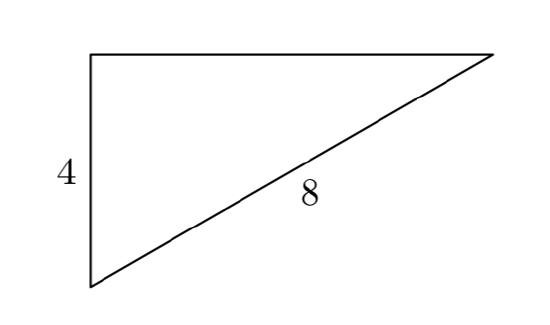
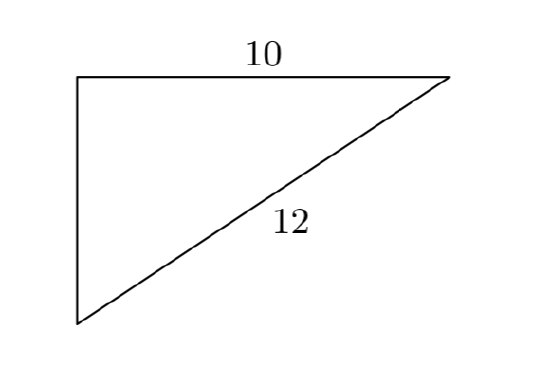
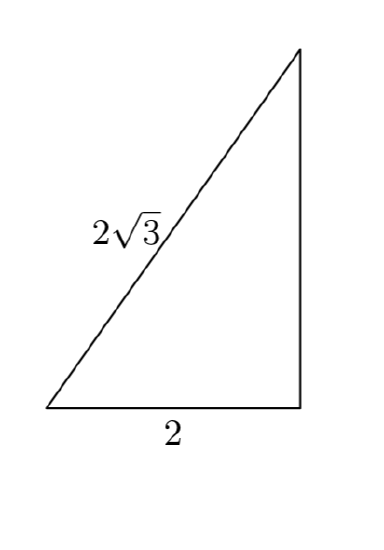
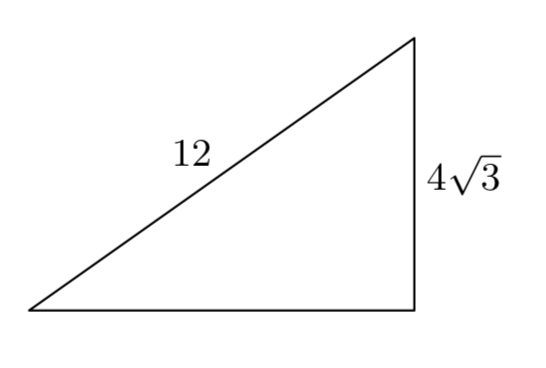
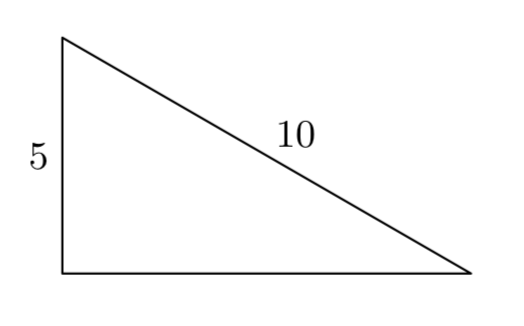
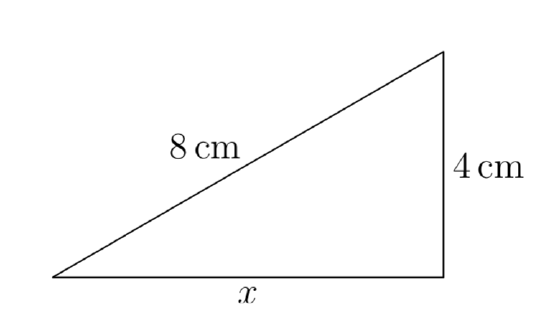
Given that the length of one leg of a right triangle is 4 centimeters and the hypotenuse has length 8 centimeters, find the length of the second leg.
Let’s begin by sketching and labeling a right triangle with the given information. We will let x represent the length of the missing leg.
Here is an important piece of advice.
The hypotenuse is the longest side of the right triangle. It is located directly opposite the right angle of the triangle. Most importantly, it is the quantity that is isolated by itself in the Pythagorean Theorem (Equation \ref{1}). Always isolate the quantity representing the hypotenuse on one side of the equation. The "legs" go on the other side of the equation.
So, taking the tip to heart, and noting the lengths of the legs and hypotenuse in Figure 1, we write
\(4^2+x^2 = 8^2\).
Square, then isolate x on one side of the equation.
\(16+x^2 = 64\)
\(x^2 = 48\)
Normally, we would take plus or minus the square root in solving this equation, but x represents the length of a leg, which must be a positive number. Hence, we take just the positive square root of 48.
\(x = \sqrt{48}\)
Of course, place your answer in simple radical form.
\(x = \sqrt{16}\sqrt{3}\)
\(x = 4\sqrt{3}\)
If need be, you can use your graphing calculator to approximate this length. To the nearest hundredth of a centimeter, \(x \approx 6.93\) centimeters.
Proof of the Pythagorean Theorem
It is not known whether Pythagoras was the first to provide a proof of the Pythagorean Theorem. Many mathematical historians think not. Indeed, it is not even known if Pythagoras crafted a proof of the theorem that bears his name, let alone was the first to provide a proof.
There is evidence that the ancient Babylonians were aware of the Pythagorean Theorem over a 1000 years before the time of Pythagoras. A clay tablet, now referred to as Plimpton 322 (see Figure 2), contains examples of Pythagorean Triples, sets of three numbers that satisfy the Pythagorean Theorem (such as 3, 4, 5).

One of the earliest recorded proofs of the Pythagorean Theorem dates from the Han dynasty (206 BC to AD 220), and is recorded in the Chou Pei Suan Ching (see Figure 3). You can see that this figure specifically addresses the case of the 3, 4, 5 right triangle. Mathematical historians are divided as to whether or not the image was meant to be part of a general proof or was just devised to address this specific case. There is also disagreement over whether the proof was provided by a more modern commentator or dates back further in time.
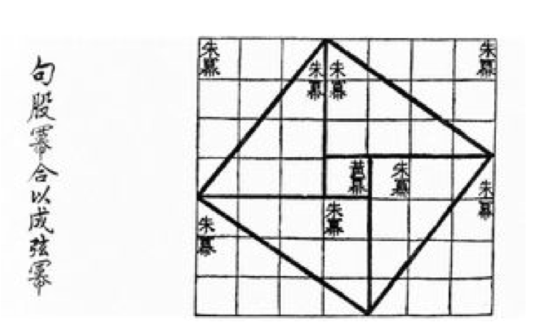
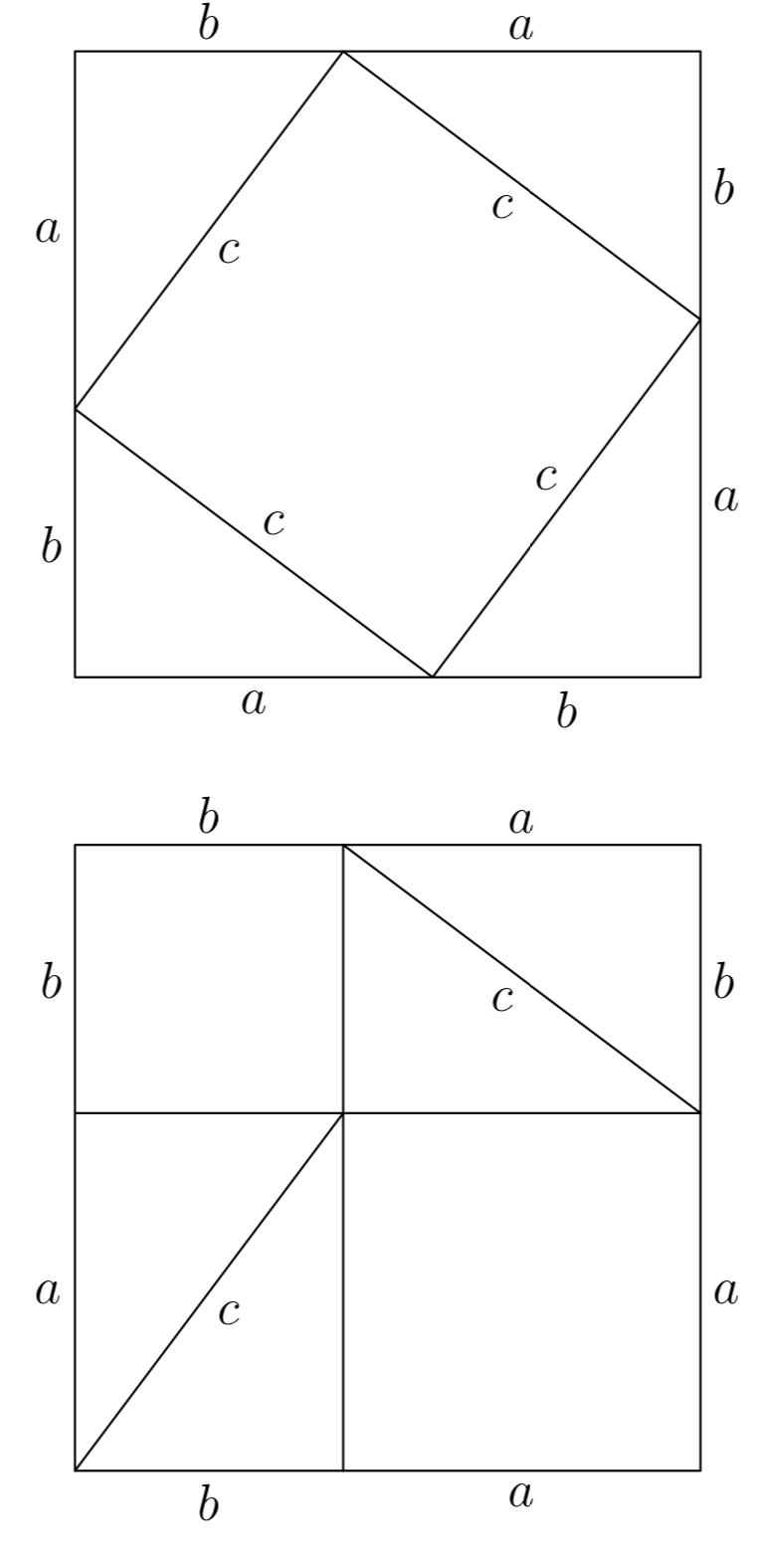
However, Figure 3 does suggest a path we might take on the road to a proof of the Pythagorean Theorem. Start with an arbitrary right triangle having legs of lengths a and b, and hypotenuse having length c, as shown in Figure 4(a).
Next, make four copies of the triangle shown in Figure 4(a), then rotate and translate them into place as shown in Figure 4(b). Note that this forms a big square that is c units on a side.
Further, the position of the triangles in Figure 4(b) allows for the formation of a smaller, unshaded square in the middle of the larger square. It is not hard to calculate the length of the side of this smaller square. Simply subtract the length of the smaller leg from the larger leg of the original triangle. Thus, the side of the smaller square has length b − a.
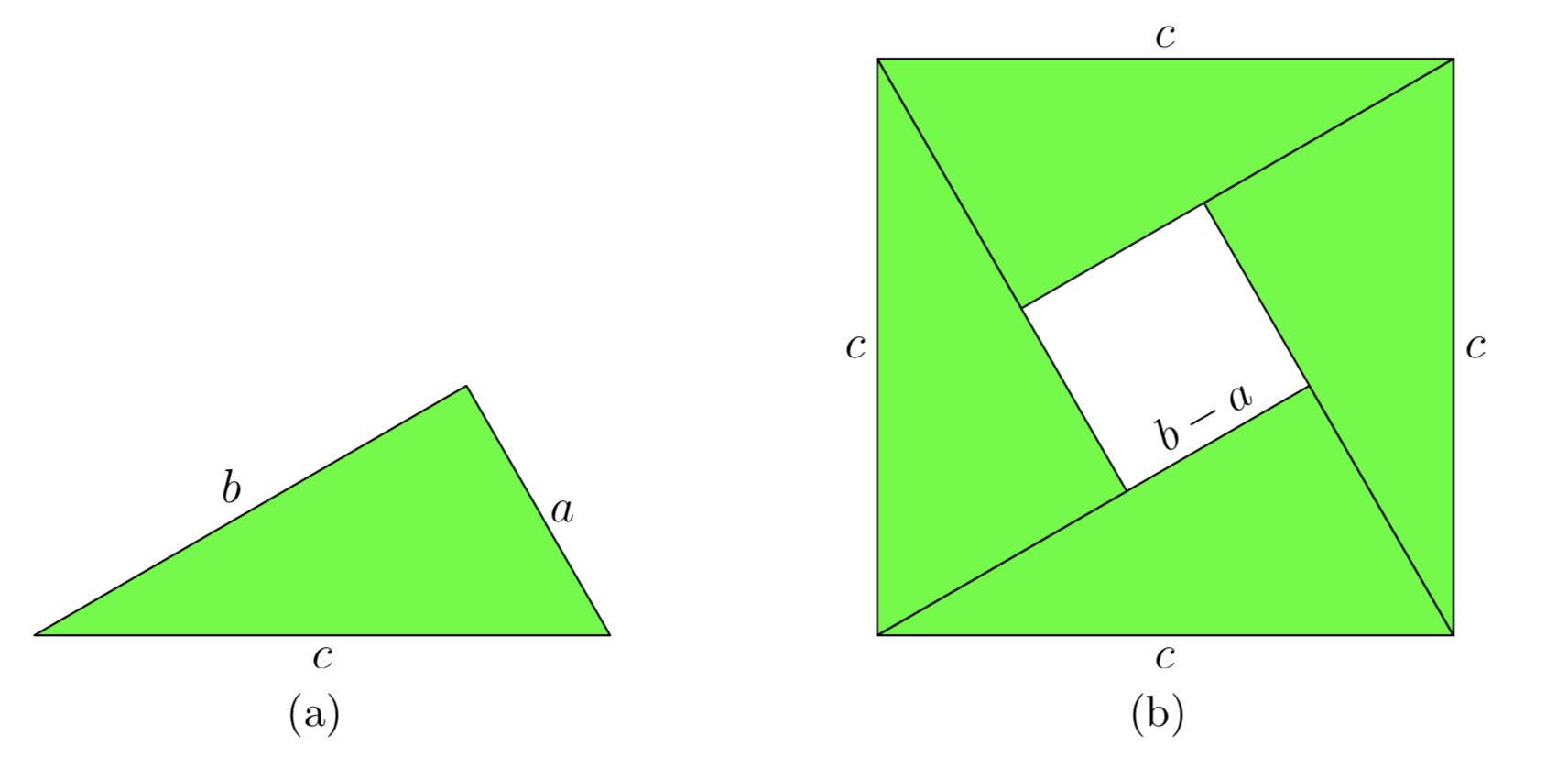
Now, we will calculate the area of the large square in Figure 4(b) in two separate ways.
- First, the large square in Figure 4(b) has a side of length c. Therefore, the area of the large square is
\(Area = c^2\).
- Secondly, the large square in Figure 4(b) is made up of 4 triangles of the same size and one smaller square having a side of length b−a. We can calculate the area of the large square by summing the area of the 4 triangles and the smaller square.
- The area of the smaller square is \((b−a)^2\).
- The area of each triangle is \(\frac{ab}{2}\). Hence, the area of four triangles of equal size is four times this number;
i.e., \(4(\frac{ab}{2})\). Thus, the area of the large square is
Area = Area of small square + \(4 \cdot\) Area of triangle
=\((b−a)^2+4(\frac{ab}{2})\).
We calculated the area of the larger square twice. The first time we got \(c^2\); the second time we got \((b−a)^2+4(\frac{ab}{2})\). Therefore, these two quantities must be equal.
\(c^2 = (b−a)^2+4(\frac{ab}{2})\).
Expand the binomial and simplify.
\(c^2 = b^2−2ab+a^2 +2ab\)
\(c^2 = b^2+a^2\)
That is,
\(a^2+b^2 = c^2\),
and the Pythagorean Theorem is proven.
Applications of the Pythagorean Theorem
In this section we will look at a few applications of the Pythagorean Theorem, one of the most applied theorems in all of mathematics. Just ask your local carpenter.
The ancient Egyptians would take a rope with 12 equally spaced knots like that shown in Figure 5, and use it to square corners of their buildings. The tool was instrumental in the construction of the pyramids.
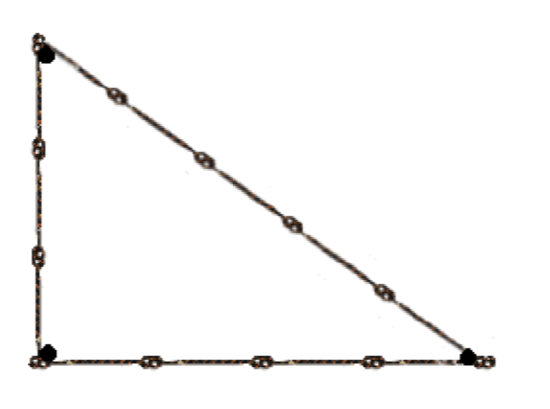
The Pythagorean theorem is also useful in surveying, cartography, and navigation, to name a few possibilities.
Let’s look at a few examples of the Pythagorean Theorem in action.
One leg of a right triangle is 7 meters longer than the other leg. The length of the hypotenuse is 13 meters. Find the lengths of all sides of the right triangle.
Let x represent the length of one leg of the right triangle. Because the second leg is 7 meters longer than the first leg, the length of the second leg can be represented by the expression x + 7, as shown in Figure 6, where we’ve also labeled the length of the hypotenuse (13 meters).
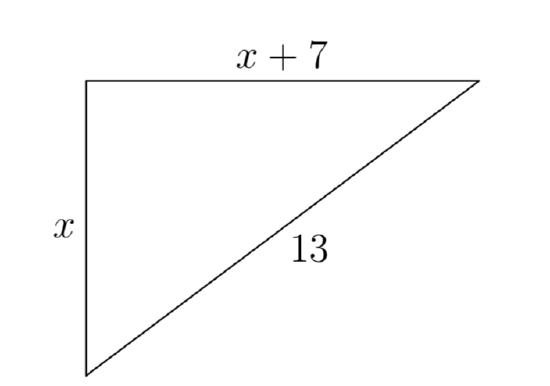
Remember to isolate the length of the hypotenuse on one side of the equation representing the Pythagorean Theorem. That is,
\(x^2+(x+7)^2 = 13^2\).
Note that the legs go on one side of the equation, the hypotenuse on the other. Square and simplify. Remember to use the squaring a binomial pattern.
\(x^2+x^2+14x+49 = 169\)
\(2x^2 +14x+49 = 169\)
This equation is nonlinear, so make one side zero by subtracting 169 from both sides of the equation.
\(2x^2+14x+49−169 = 0\)
\(2x^2 +14x−120 = 0\)
Note that each term on the left-hand side of the equation is divisible by 2. Divide both sides of the equation by 2.
\(x^2+7x−60 = 0\)
Let’s use the quadratic formula with a = 1, b = 7, and c = −60.
\(x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−7 \pm \sqrt{7^2 −4(1)(−60)}}{2(1)}\)
Simplify.
\(x = \frac{−7 \pm \sqrt{289}}{2}\)
Note that 289 is a perfect square (\(17^2 = 289\)). Thus,
\(x = \frac{−7 \pm 17}{2}\).
Thus, we have two solutions,
x = 5 or x = −12.
Because length must be a positive number, we eliminate −12 from consideration. Thus, the length of the first leg is x = 5 meters. The length of the second leg is x+7, or 12 meters.
Check. Checking is an easy matter. The legs are 5 and 12 meters, respectively, and the hypotenuse is 13 meters. Note that the second leg is 7 meters longer than the first. Also,
\(5^2+12^2 = 25+144 = 169\),
which is the square of 13.
The integral sides of the triangle in the previous example, 5, 12, and 13, are an example of a Pythagorean Triple.
A set of positive integers a, b, and c, is called a Pythagorean Triple if they satisfy the Pythagorean Theorem; that is, if
\(a^2+b^2 = c^2\).
If the greatest common factor of a, b, and c is 1, then the triple (a, b, c) is called a primitive Pythagorean Triple.
Thus, for example, the Pythagorean Triple (5, 12, 13) is primitive. Let’s look at another example.
If (a,b,c) is a Pythagorean Triple, show that any positive integral multiple is also a Pythagorean Triple.
Thus, if the positive integers (a, b, c) is a Pythagorean Triple, we must show that(ka, kb, kc), where k is a positive integer, is also a Pythagorean Triple.
However, we know that
\(a^2+b^2 = c^2\).
Multiply both sides of this equation by \(k^2\).
\(k^{2}a^2+k^{2}b^2 = k^{2}c^2\)
This last result can be written
\((ka)^2 + (kb)^2 = (kc)^2\).
Hence, (ka, kb, kc) is a Pythagorean Triple.
Hence, because (3, 4, 5) is a Pythagorean Triple, you can double everything to get another triple (6, 8, 10). Note that \(6^2 + 8^2 = 10^2\) is easily checked. Similarly, tripling gives another triple (9, 12, 15), and so on.
In Example 5, we showed that (5, 12, 13) was a triple, so we can take multiples to generate other Pythagorean Triples, such as (10, 24, 26) or (15, 36, 39), and so on.
Formulae for generating Pythagorean Triples have been know since antiquity.
The following formula for generating Pythagorean Triples was published in Euclid’s (325–265 BC) Elements, one of the most successful textbooks in the history of mathematics. If m and n are positive integers with m > n, show
\(a = m^2−n^2\),
b = 2mn, (7)
\(c = m^2+n^2\),
generates Pythagorean Triples.
We need only show that the formulae for a, b, and c satisfy the Pythagorean Theorem. With that is mind, let’s first compute \(a^2+b^2\).
\(a^2+b^2 = (m^2−n^2)^2+(2mn)^2\)
= \(m^4−2m^{2}n^{2}+n^4+4m^{2}n^2\)
= \(m^4+2m^{2}n^2+n^4\)
On the other hand,
\(c^2 = (m^2+n^2)^2\)
= \(m^4+2m^{2}n^2+n^4\).
Hence, \(a^2+b^2 = c^2\), and the expressions for a, b, and c form a Pythagorean Triple.
It is both interesting and fun to generate Pythagorean Triples with the formulae from Example 6. Choose m = 4 and n = 2, then
\(a = m^2−n^2 = (4)^2−(2)^2 = 12\),
\(b = 2mn = 2(4)(2) = 16\),
\(c = m^2+n^2 =(4)^2+(2)^2 = 20\).
It is easy to check that the triple (12, 16, 20) will satisfy \(12^2+16^2 = 20^2\). Indeed, note that this triple is a multiple of the basic (3, 4, 5) triple, so it must also be a Pythagorean Triple.
It can also be shown that if m and n are relatively prime, and are not both odd or both even, then the formulae in Example 6 will generate a primitive Pythagorean Triple. For example, choose m = 5 and n = 2. Note that the greatest common divisor of m = 5 and n = 2 is one, so m and n are relatively prime. Moreover, m is odd while n is even. These values of m and n generate
\(a = m^2−n^2 = (5)^2−(2)^2 = 21\),
\(b = 2mn = 2(5)(2) = 20\),
\(c = m^2+n^2 = (5)^2+(2)^2 = 29\).
Note that
\(21^2+20^2 = 441+400 = 841 = 29^2\).
Hence, (21, 20, 29) is a Pythagorean Triple. Moreover, the greatest common divisor of 21, 20, and 29 is one, so (21, 20, 29) is primitive.
The practical applications of the Pythagorean Theorem are numerous.
A painter leans a 20 foot ladder against the wall of a house. The base of the ladder is on level ground 5 feet from the wall of the house. How high up the wall of the house will the ladder reach?
Consider the triangle in Figure 7. The hypotenuse of the triangle represents the ladder and has length 20 feet. The base of the triangle represents the distance of the base of the ladder from the wall of the house and is 5 feet in length. The vertical leg of the triangle is the distance the ladder reaches up the wall and the quantity we wish to determine.
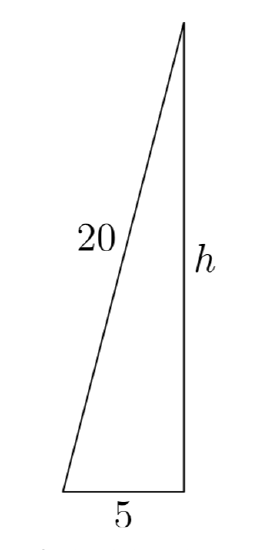
Applying the Pythagorean Theorem,
\(5^2+h^2 = 20^2\).
Again, note that the square of the length of the hypotenuse is the quantity that is isolated on one side of the equation.
Next, square, then isolate the term containing h on one side of the equation by subtracting 25 from both sides of the resulting equation.
\(25+h^2 = 400\)
\(h^2 = 375\)
We need only extract the positive square root.
\(h = \sqrt{375}\)
We could place the solution in simple form, that is, \(h = 5\sqrt{15}\), but the nature of the problem warrants a decimal approximation. Using a calculator and rounding to the nearest tenth of a foot,
\(h \approx 19.4\).
Thus, the ladder reaches about 19.4 feet up the wall.
The Distance Formula
We often need to calculate the distance between two points P and Q in the plane. Indeed, this is such a frequently recurring need, we’d like to develop a formula that will quickly calculate the distance between the given points P and Q. Such a formula is the goal of this last section.
Let P(x1, y1) and Q(x2, y2) be two arbitrary points in the plane, as shown in Figure 8(a) and let d represent the distance between the two points.
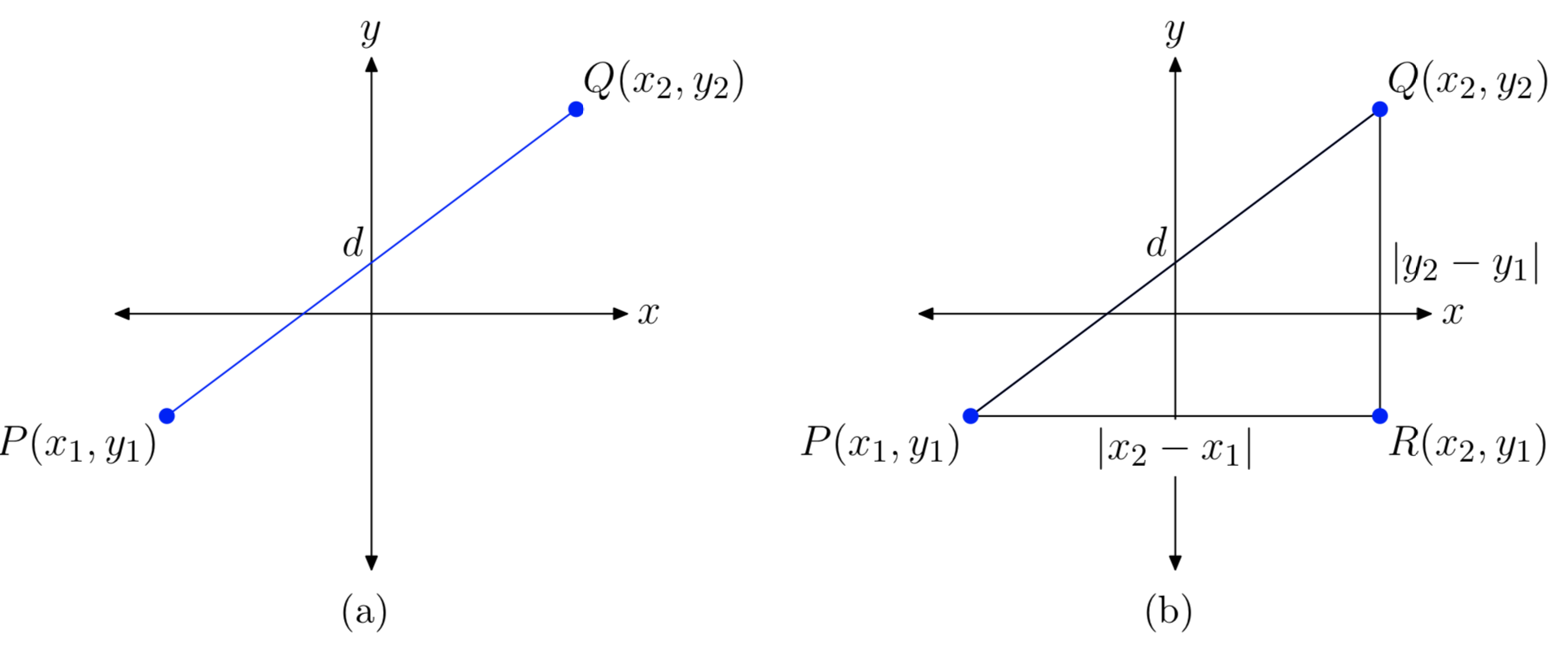
To find the distance d, first draw the right triangle △PQR, with legs parallel to the axes, as shown in Figure 8(b). Next, we need to find the lengths of the legs of the right triangle △PQR.
- The distance between P and R is found by subtracting the x coordinate of P from the x-coordinate of R and taking the absolute value of the result. That is, the distance between P and R is \(|x_{2}−x_{1}|\).
- The distance between R and Q is found by subtracting the y-coordinate of R from the y-coordinate of Q and taking the absolute value of the result. That is, the distance between R and Q is \(|y_{2}−y_{1}|\).
We can now use the Pythagorean Theorem to calculate d. Thus,
\(d^2 = (|x_{2}−x_{1}|)^2+(|y_{2}−y_{1}|)^2\).
However, for any real number a,
\((|a|)^2 = |a|·|a| = |a^2| = a^2\),
because a2 is nonnegative. Hence, \((|x_{2} − x_{1}|)^2 = (x_{2} − x_{1})^2 and (|y_{2} − y_{1}|)^2 = (y_{2} − y_{1})^2\) and we can write
\(d^2 = (x_{2}−x_{1})^2+(y_{2}−y_{1})^2\).
Taking the positive square root leads to the Distance Formula.
Let P (x1, y1) and Q(x2, y2) be two arbitrary points in the plane. The distance d between the points P and Q is given by the formula
\(d = \sqrt{(x_{2}−x_{1})^2+(y_{2}−y_{1})^2}\). (9)
The direction of subtraction is unimportant. Because you square the result of the subtraction, you get the same response regardless of the direction of subtraction (e.g.\((5 − 2)^2 = (2 − 5)^2\)). Thus, it doesn’t matter which point you designate as the point P, nor does it matter which point you designate as the point Q. Simply subtract x- coordinates and square, subtract y-coordinates and square, add, then take the square root.
Let’s look at an example.
Find the distance between the points P (−4, −2) and Q (4, 4).
It helps the intuition if we draw a picture, as we have in Figure 9. One can now take a compass and open it to the distance between points P and Q. Then you can place your compass on the horizontal axis (or any horizontal gridline) to estimate the distance between the points P and Q. We did that on our graph paper and estimate the distance \(d \approx 10\).
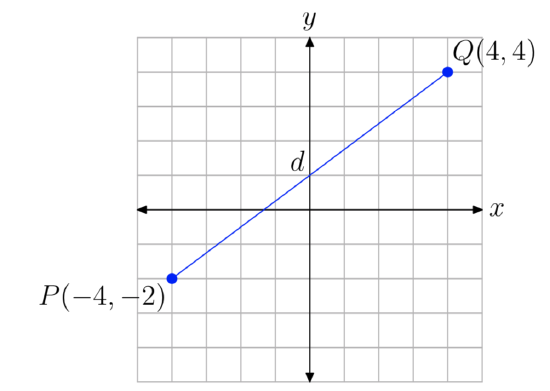
Let’s now use the distance formula to obtain an exact value for the distance d. With \((x_{1}, y_{1})\) = P (−4, −2) and \((x_{2}, y_{2})\) = Q (4, 4),
\(d = \sqrt{(x_{2}−x_{1})^2+(y_{2}−y_{1})^2}\)
= \(\sqrt{(4−(−4))^2+(4−(−2))^2}\)
= \(\sqrt{8^2+6^2}\)
= \(\sqrt{64+36}\)
= \(\sqrt{100}\)
= 10.
It’s not often that your exact result agrees with your approximation, so never worry if you’re off by just a little bit.
Exercise
In Exercises 1-8, state whether or not the given triple is a Pythagorean Triple. Give a reason for your answer.
(8, 15, 17)
- Answer
-
Yes, because \(8^2 + 15^2 = 17^2\)
(7, 24, 25)
(8, 9, 17)
- Answer
-
No, because \(8^2+9^2 \ne 17^2\)
(4, 9, 13)
(12, 35, 37)
- Answer
-
Yes, because \(12^2 + 35^2 = 37^2\)
(12, 17, 29)
(11, 17, 28)
- Answer
-
No, because \(11^2 + 17^2 \ne 28^2\)
(11, 60, 61)
In Exercises 9-16, set up an equation to model the problem constraints and solve. Use your answer to find the missing side of the given right triangle. Include a sketch with your solution and check your result.
In Exercises 17-20, set up an equation that models the problem constraints. Solve the equation and use the result to answer the question. Look back and check your result.
The legs of a right triangle are consecutive positive integers. The hypotenuse has length 5. What are the lengths of the legs?
- Answer
-
The legs have lengths 3 and 4.
The legs of a right triangle are consecutive even integers. The hypotenuse has length 10. What are the lengths of the legs?
One leg of a right triangle is 1 centimeter less than twice the length of the first leg. If the length of the hypotenuse is 17 centimeters, find the lengths of the legs.
- Answer
-
The legs have lengths 8 and 15 centimeters.
One leg of a right triangle is 3 feet longer than 3 times the length of the first leg. The length of the hypotenuse is 25 feet. Find the lengths of the legs.
Pythagoras is credited with the following formulae that can be used to generate Pythagorean Triples.
a = m
\(b = \frac{m^2−1}{2}\),
\(c = \frac{m^2+1}{2}\)
Use the technique of Example 6 to demonstrate that the formulae given above will generate Pythagorean Triples, provided that m is an odd positive integer larger than one. Secondly, generate at least 3 instances of Pythagorean Triples with Pythagoras’s formula.
- Answer
-
(3, 4, 5), (5, 12, 13), and (7, 24, 25), with m = 3, 5, and 7, respectively.
Plato (380 BC) is credited with the following formulae that can be used to generate Pythagorean Triples.
\(a = 2m\)
\(b = m^2 − 1\),
\(c = m^2 + 1\)
Use the technique of Example 6 to demonstrate that the formulae given above will generate Pythagorean Triples, provided that m is a positive integer larger than 1. Secondly, generate at least 3 instances of Pythagorean Triples with Plato’s formula.
In Exercises 23-28, set up an equation that models the problem constraints. Solve the equation and use the result to answer. Look back and check your answer.
Fritz and Greta are planting a 12-foot by 18-foot rectangular garden, and are laying it out using string. They would like to know the length of a diagonal to make sure that right angles are formed. Find the length of a diagonal. Approximate your answer to within 0.1 feet.
- Answer
-
21.63 ft
Angelina and Markos are planting a 20-foot by 28-foot rectangular garden, and are laying it out using string. They would like to know the length of a diagonal to make sure that right angles are formed. Find the length of a diagonal. Approximate your answer to within 0.1 feet.
The base of a 36-foot long guy wire is located 16 feet from the base of the telephone pole that it is anchoring. How high up the pole does the guy wire reach? Approximate your answer to within 0.1.
- Answer
-
32.25 ft
The base of a 35-foot long guy wire is located 10 feet from the base of the telephone pole that it is anchoring. How high up the pole does the guy wire reach? Approximate your answer to within 0.1 feet.
A stereo receiver is in a corner of a 13-foot by 16-foot rectangular room. Speaker wire will run under a rug, diagonally, to a speaker in the far corner. If 3 feet of slack is required on each end, how long a piece of wire should be purchased? Approximate your answer to within 0.1 feet.
- Answer
-
26.62 ft
A stereo receiver is in a corner of a 10-foot by 15-foot rectangular room. Speaker wire will run under a rug, diagonally, to a speaker in the far corner. If 4 feet of slack is required on each end, how long a piece of wire should be purchased? Approximate your answer to within 0.1 feet.
In Exercises 29-38, use the distance formula to find the exact distance between the given points.
(−8, −9) and (6, −6)
- Answer
-
\(\sqrt{205}\)
(1, 0) and (−9, −2)
(−9, 1) and (−8, 7)
- Answer
-
\(\sqrt{37}\)
(0, 9) and (3, 1)
(6, −5) and (−9, −2)
- Answer
-
\(\sqrt{234} = 3\sqrt{26}\)
(−5, 6) and (1, 4)
(−7, 7) and (−3, 6)
- Answer
-
\(\sqrt{17}\)
(−7, −6) and (−2, −4)
(4, −3) and (−9, 6)
- Answer
-
\(\sqrt{250} = 5\sqrt{10}\)
(−7, −1) and (4, −5)
In Exercises 39-42, set up an equation that models the problem constraints. Solve the equation and use the result to answer the question. Look back and check your result.
Find k so that the point (4, k) is \(2\sqrt{2}\) units away from the point (2, 1).
- Answer
-
k = 3, −1.
Find k so hat the point (k, 1) is \(2\sqrt{2}\) units away from the point (0, −1)
Find k so hat the point (k, 1) is \(\sqrt{17}\) units away from the point (2, −3)
- Answer
-
k = 1, 3.
Find k so that the point (−1, k) is \(\sqrt{13}\) units away from the point (−4, −3).
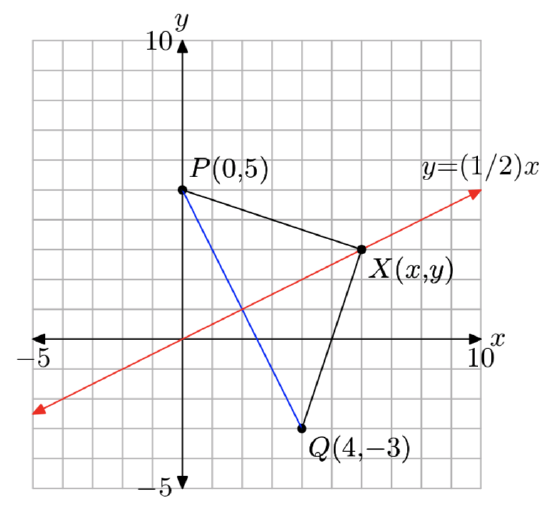
Set up a coordinate system on a sheet of graph paper. Label and scale each axis. Plot the points P (0, 5) and Q (4, −3) on your coordinate system.
a) Plot several points that are equidistant from the points P and Q on your coordinate system. What graph do you get if you plot all points that are equidistant from the points P and Q? Determine the equation of the graph by examining the resulting image on your coordinate system.
b) Use the distance formula to find the equation of the graph of all points that are equidistant from the points P and Q. Hint: Let (x, y) represent an arbitrary point on the graph of all points equidistant from points P and Q. Calculate the distances from the point (x, y) to the points P and Q separately, then set them equal and simplify the resulting equation. Note that this analytical approach should provide an equation that matches that found by the graphical approach in part (a).
Set up a coordinate system on a sheet of graph paper. Label and scale each axis. Plot the point P (0, 2) and label it with its coordinates. Draw the line y = −2 and label it with its equation.
a) Plot several points that are equidistant from the point P and the line y = −2 on your coordinate system. What graph do you get if you plot all points that are equidistant from the points P and the line y = −2.
b) Use the distance formula to find the equation of the graph of all points that are equidistant from the points P and the line y = −2. Hint: Let(x, y) represent an arbitrary point on the graph of all points equidistant from points P and the line y = −2. Calculate the distances from the point(x,y) to the points P and the line y = −2 separately, then set them equal and simplify the resulting equation.
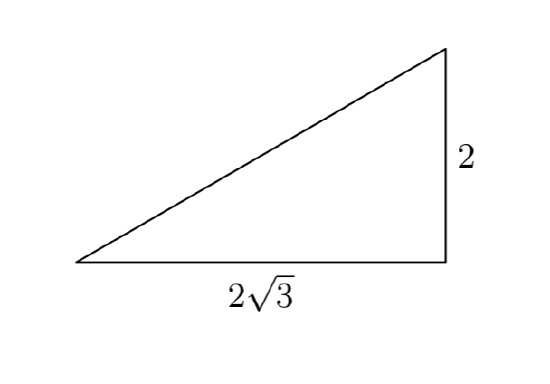
Copy the following figure onto a sheet of graph paper. Cut the pieces of the first figure out with a pair of scissors, then rearrange them to form the second figure. Explain how this proves the Pythagorean Theorem.
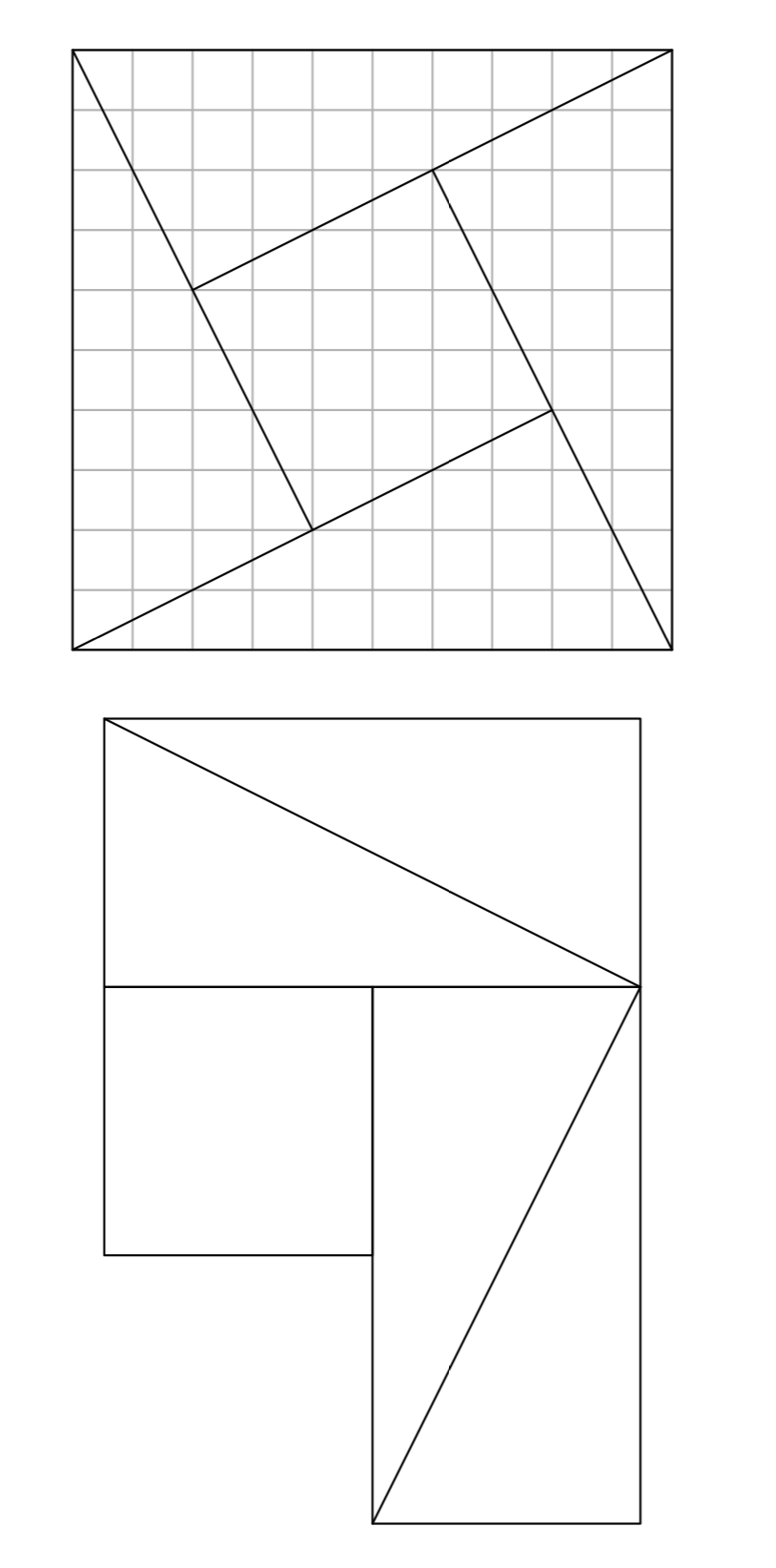
Compare this image to the one that follows and explain how this proves the Pythagorean Theorem.