9.5: Radical Equations
- Page ID
- 19738
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Radical Equations
In this section we are going to solve equations that contain one or more radical expressions. In the case where we can isolate the radical expression on one side of the equation, we can simply raise both sides of the equation to a power that will eliminate the radical expression. For example, if
\(\sqrt{x−1} = 2\) (1)
then we can square both sides of the equation, eliminating the radical.
\(\sqrt{x−1}^2 = (2)^2\)
x−1=4
Now that the radical is eliminated, we can appeal to well understood techniques to solve the equation that remains. In this case, we need only add 1 to both sides of the equation to obtain
x = 5.
This solution is easily checked. Substitute x = 5 in the original equation(1).
\(\sqrt{x−1} = 2\)
\(\sqrt{5−1} = 2\)
\(\sqrt{4} = 2\)
The last line is valid because the “positive square root of 4” is indeed 2.
This seems pretty straight forward, but there are some subtleties. Let’s look at another example, one with an equation quite similar to equation.
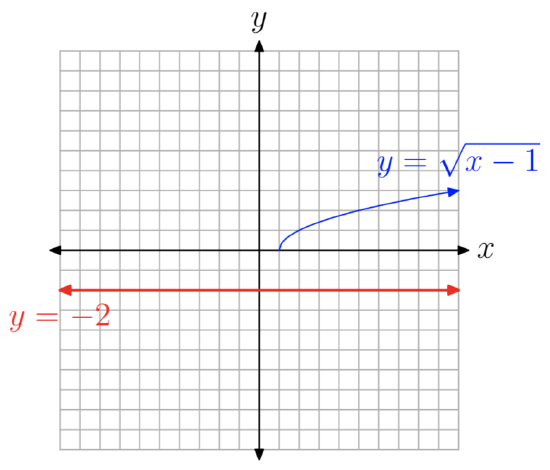
Solve the equation \(\sqrt{x−1} = −2\) for x.
If you carefully study the equation
\(\sqrt{x−1} = −2\) (3)
you might immediately detect a difficulty. The left-hand side of the equation calls for a “positive square root,” but the right-hand side of the equation is negative. Intuitively, there can be no solutions.
A look at the graphs of each side of the equation also reveals the problem. The graphs of \(y = \sqrt{x−1}\) and y = −2 are shown in Figure 1. Note that the graphs do not intersect, so the equation \(\sqrt{x−1} = −2\) has no solution.
However, note what happens when we square both sides of equation(3).
\((\sqrt{x − 1})^2 = (−2)^2\)
\(x−1=4\) (4)
This result is identical to the result we got when we squared both sides of the equation \(\sqrt{x−1} = 2\) above. If we continue, adding 1 to both sides of the equation, we get
x = 5.
But this cannot be correct, as both intuition and the graphs in Figure 1 have shown that the equation \(\sqrt{x−1} = −2\) has no solution.
Let's check the solution x= 5 in the original equation.
\(\sqrt{x−1} = −2\)
\(\sqrt{5−1} = −2\)
\(\sqrt{4} = −2\)
Because the “positive square root of 4” does not equal −2, this last line is incorrect and the solution x = 5 does not check in the equation \(\sqrt{x−1} = −2\). Because the only solution we found does not check, the equation has no solutions.
The discussion in Example 2 dictates caution.
Whenever you square both sides of an equation, there is a possibility that you can introduce extraneous solutions, “extra” solutions that will not check in the original problem.
There is only one way to avoid this dilemma of extraneous equations.
Whenever you square both sides of an equation, you must check each of your solutions in the original equation. This is the only way you can be sure you have a valid solution.
Squaring a Binomial
As we’ve seen time and time again, the squaring a binomial pattern is of utmost importance.
If a and b are any real numbers, then
\((a+b)^2 = a^2+2ab+b^2\).
The squaring a binomial pattern will play a major role in the rest of the examples in this section.
Let’s look at some examples of its use.
Expand and simplify \((1+\sqrt{x})^2\) by using the squaring a binomial pattern. Assume that \(x \ge 0\).
The assumption that \(x \ge 0\) is required, otherwise the expression \(\sqrt{x}\) involves the square root of a negative number, which is not a real number.
The squaring a binomial pattern tells us to square the first and second terms. However, there is also a middle term, which is found by taking the product of the first and second terms, then multiplying the result by 2.
\((1 + \sqrt{x})^2 = (1)^2 + 2(1)(\sqrt{x}) + (\sqrt{x})^2\)
=\(1+2\sqrt{x}+x\)
Let’s look at another example.
Expand and simplify \((\sqrt{x+1}−\sqrt{x})^2\) by using the squaring a binomial pattern. Comment on the domain of this expression.
In order for this expression to make sense, we must avoid taking the square root of a negative number. Hence, both expressions under the square roots must be nonnegative (positive or zero). That is,
\[\begin{array}{ccc} {x+1 \ge 0}&{\text{and}}&{x \ge 0}\\ \nonumber \end{array} \nonumber \]
Solving each of these inequalities independently, we get the fact that
\[\begin{array}{ccc} {x \ge −1}&{\text{and}}&{x \ge 0}\\ \nonumber \end{array} \nonumber \]
Because of the word “and,” the requested domain is the set of all numbers that satisfy both inequalities, namely, the set of all real numbers that are greater than or equal to zero. That is, the domain of the expression is \({x : x ≥ 0}\).
We will now expand the expression \((\sqrt{x+1}−\sqrt{x})^2\) using the squaring a binomial pattern.
\((\sqrt{x+1}−\sqrt{x})^2 = (\sqrt{x+1})^2−2(\sqrt{x+1})(\sqrt{x})+(\sqrt{x})^2\)
= \(x+1+2\sqrt{(x+1)x}+x\)
= \(2x+1+2\sqrt{x^2 +x}\)
Isolate the Radical
Our mantra will be the strategy phrase “Isolate the radical.”
When you solve equations containing one radical, isolate the radical by itself on one side of the equation.
Although this is not always possible (some equations might contain more than one radical expression), it is possible in our next example.
Solve the equation
\(1+\sqrt{4x+13} = 2x\) for x (9)
Let’s look at a graphing calculator solution. We’ve loaded the left- and right-hand sides of \(1+\sqrt{4x+13} = 2x\) into Y1 and Y2, respectively, as shown in Figure 2(a). We then use 6:ZStandard and the intersect utility on the CALC menu to determine the coordinates of the point of intersection of \(y = 1+\sqrt{4x+13}\) and y = 2x, as shown in Figure 2(b).
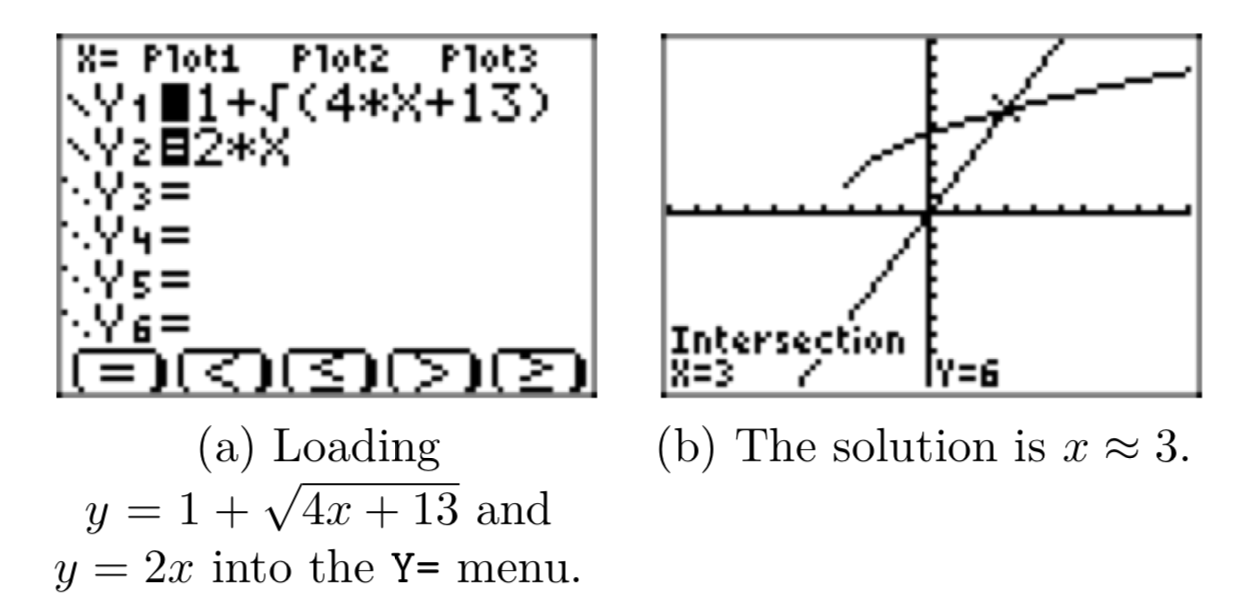
We will now present an algebraic solution, but note that we are forewarned that there is only one solution and we believe that the solution is \(x \approx 3\). Of course, this is only an approximation, as is always the case when we pick up our calculator (our approximating machine).
Chant the strategy phrase “isolate the radical,” then isolate the radical on one side of the equation. We will accomplish this directive by subtracting 1 from both sides of the equation.
\(1+\sqrt{4x+13} = 2x\)
\(\sqrt{4x+13} = 2x−1\)
Next, square both sides of the equation.
\((\sqrt{4x + 13})^2 = (2x−1)^2\)
Squaring eliminates the radical on the left, but we must use the squaring a binomial pattern to square the binomial on the right-side of the equation.
\(4x+13 = (2x)^2−2(2x)(1)+(1)^2\)
\(4x+13 = 4x^2−4x+1\)
We’ve succeed in clearing all square roots from the equation with our “isolate the radical” strategy. The equation that remains is nonlinear (there is a power of x higher than 1), so we want to make one side of the equation equal to zero. We will do this by subtracting 4x and 13 from both sides of the equation.
\(0 = 4x^2−4x+1−4x−13\)
\(0 = 4x^2−8x−12\)
At this point, note that each term on the right-hand side of the equation is divisible by 4. Divide both sides of the equation by 4, then use the ac-test to factor the result.
\(0 = x^2−2x−3\)
0 = (x−3)(x+1)
Set each factor on the right-hand side of this last equation to obtain the solutions x = 3 and x = −1.
Note that x = 3 matches the solution found by graphing in Figure 2(b). However, an “extra” solution x = −1 has appeared. Remember that we squared both sides of the original equation, so it is possible that extraneous solutions have been introduced. We need to check each of our solutions by substituting them into the original equation(9).
Our graph in Figure 2(b) adds credence to the analytical solution x = 3, so let’s check that one first. Substitute x = 3 in the original equation.
\(1+\sqrt{4x+13} = 2x\)
\(1+\sqrt{4(3)+13} = 2(3)\)
\(1+ \sqrt{25} = 6\)
\(1+5 = 6\)
Clearly, x = 3 checks and is a valid solution.
Next, let’s check the “suspect” solution x = −1 by substituting it into the original equation.
\(1+\sqrt{4x+13} = 2x\)
\(1 + \sqrt{4(−1) + 13} = 2(−1)\)
\(1+\sqrt{9} = −2\)
\(1+3 = −2\)
Clearly, x = −1 does not check and is not a solution.
Thus, the only solution of \(1+\sqrt{4x+13} = 2x\) is x = 3. Readers should take note how that graphical solution and the analytic solution complement one another.
Before looking at another example, let’s look at one of the most common mistakes made in the algebraic solution of equation.
A Common Algebraic Mistake
In this section we discuss one of the most common algebraic mistakes encountered when solving equations that contain radical expressions.
Many of the computations in this section are incorrect. They are examples of common algebra mistakes made when solving equations containing radicals. Keep this in mind and read the material in this section very carefully.
When presented with the equation
\(1+\sqrt{4x+13} = 2x\), (11)
some will square both sides of the equation in the following manner.
\((1)^2 + (\sqrt{4x+13})^2 = (2x)^2\). (12)
arriving at
\(1+4x+13 = 4x^2\).
Make one side zero, then divide both sides of the resulting equation by 2.
\(0=4x^2 −4x−14\)
\(0=2x^2 −2x−7\)
The careful reader will already realize that we’ve traveled the wrong path, as this result is quite different from that at a similar point in the solution of Example 8. However, we can continue with the solution by using the quadratic formula to solve the last equation for x. When we compare \(2x^2−2x−7\) with \(ax^2+bx+c\), note that a = 2, b=−2, and c=−7. Thus,
\(x = \frac{−b \pm \sqrt{b^2−4ac}}{2a}\)
= \(\frac{−(−2) \pm \sqrt{(−2)^2−4(2)(−7)}}{2(2)}\)
= \(\frac{2 \pm \sqrt{60}}{4}\)
However, neither of these “solutions” represent the correct solution found in Example 8, namely, x = 3. So, what have we done wrong?
The mistake occurred in the very first step when we squared both sides of the equation(11). Indeed, to get equation(12), we did not actually square both sides of equation(11). Rather, we squared each of the individual terms on each side of the equation.
This is a serious mistake. In essence, we started with an equation having the form
a + b = c, (13)
then squared “both sides” in the following manner.
\(a^2 + b^2 = c^2\). (14)
This is not valid. For example, start with
2 + 3 = 5,
a completely valid equation as the sum of 2 and 3 is 5. Now “square" as we did in equation (14) to get
\(2^2 + 3^2 = 5^2\).
However, note that this simplifies as
4+9 = 25,
so we no longer have a valid equation.
The mistake made here is that we squared each of the individual terms on each side of the equation instead of squaring “each side” of the equation. If we had done that, we would have been all right, as is seen in this calculation.
2+3=5
\((2+3)^2 =5^2\)
\(2^2 +2(2)(3)+3^2 =5^2\)
4+12+9 = 25
Just remember, a+b = c does not imply \(a^2+b^2 = c^2\).
We will now return to correct computations.
More than One Radical
Let’s look at an equation that contains more than one radical.
Solve the equation
\(\sqrt{2x}+\sqrt{2x+3} = 3\) (17)
for x.
We’ll start with a graphical solution of the equation. First, load the equations \(y = \sqrt{2x}+\sqrt{2x+3}\) and y = 3 into the Y = menu, as shown in Figure3(a).
We cannot take the square root of a negative number, so when we consider the function defined by the equation \(y = \sqrt{2x}+\sqrt{2x+3}\), both expressions under the radicals must be nonnegative. That is,
\[\begin{array}{ccc} {2x \ge 0}&{\text{and}}&{2x+3 \ge 0}\\ \nonumber \end{array} \nonumber \]
Solving each of these independently,
\[\begin{array}{ccc} {x \ge 0}&{\text{and}}&{x \ge −\frac{3}{2}}\\ \nonumber \end{array} \nonumber \]
The numbers that are greater than or equal to zero and greater than or equal to \(−\frac{3}{2}\) are the numbers greater than or equal to zero. Hence, the domain of the function defined by the equation \(y = \sqrt{2x}+\sqrt{2x+3}\), is {x : \(x \ge 0\)}. Thus, it should not come as a shock when the graph of \(y = \sqrt{2x}+\sqrt{2x+3}\) lies entirely to the right of zero, as shown in Figure 3(b).
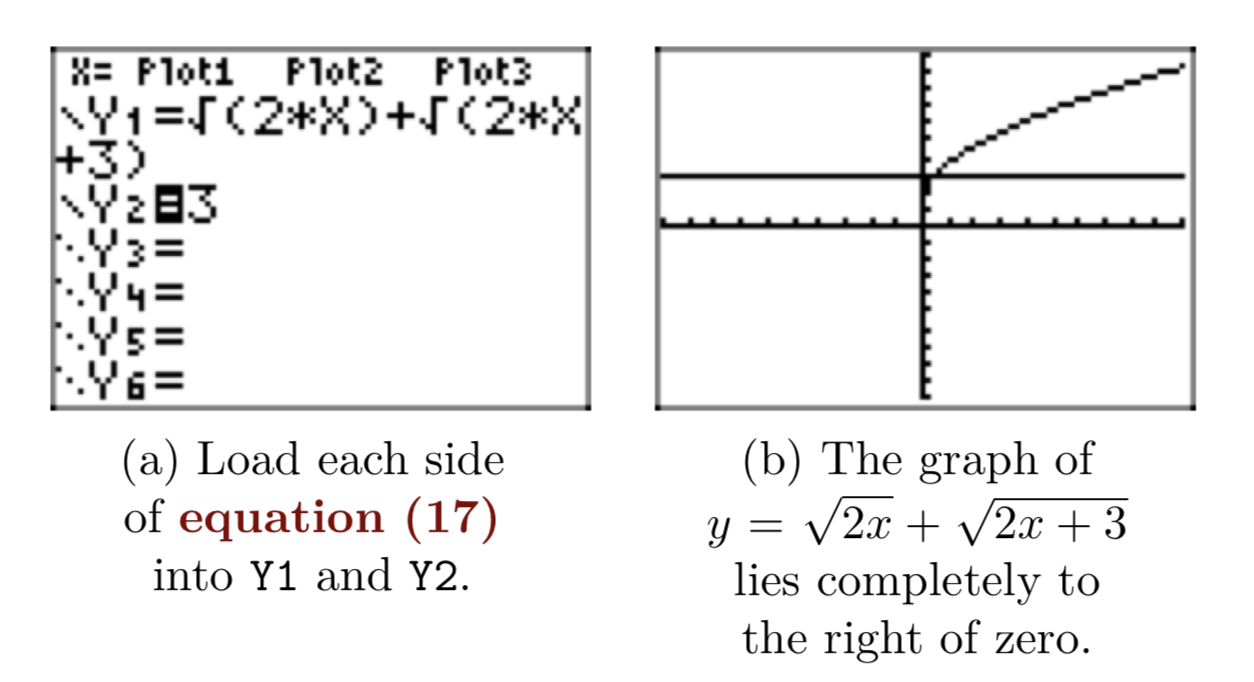
It’s a bit difficult to see the point of intersection in Figure 3(b), so let’s adjust the WINDOW settings as shown in Figure 4(a). As you can see Figure 4(b), this highlights the point of intersection a bit more clearly and the 5:intersect utility in the CALC menu finds the point of intersection shown in Figure 4(b).
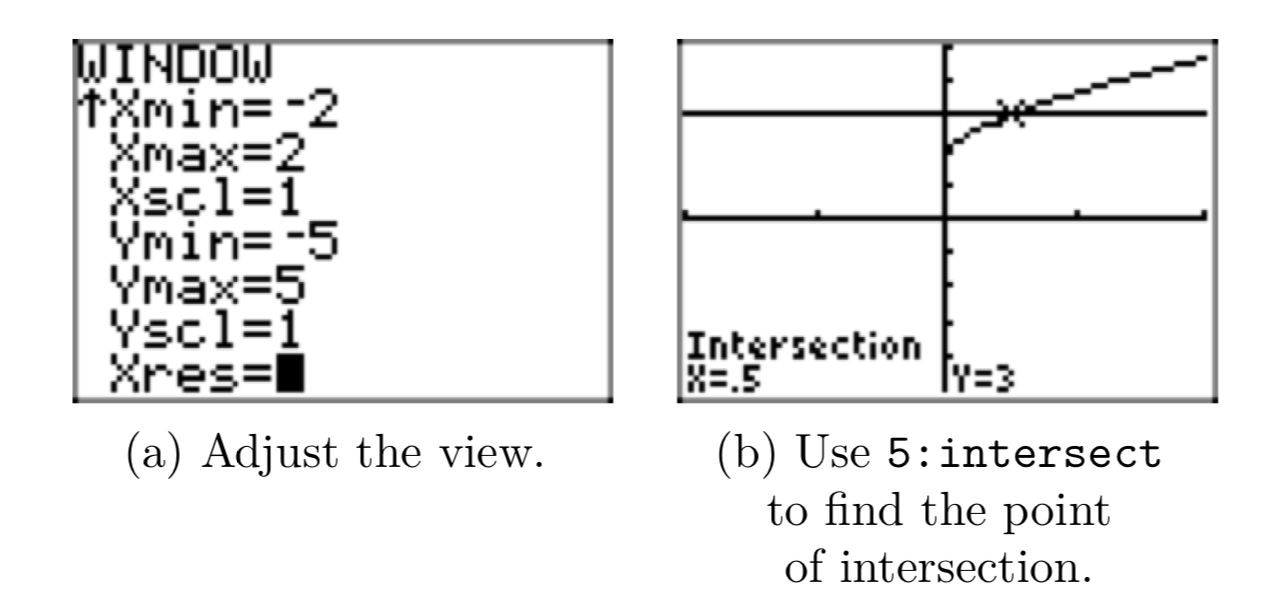
The graphing calculator reports one solution (there’s only one point of intersection), and the x-value of the point of intersection is approximately \(x \approx 0.5\).
Now, let’s look at an algebraic solution. Since are two radical expressions in this equation, we will isolate one of them on one side of the equation. We choose to isolate the more complex of the two radical expressions on the left-hand side of the equation, then square both sides of the resulting equation.
\(\sqrt{2x}+\sqrt{2x+3} = 3\)
\(\sqrt{2x+3} = 3−\sqrt{2x}\)
\((\sqrt{2x+3})^2 = (3−\sqrt{2x})^2\)
On the left, squaring eliminates the radical. To square the binomial on the right, we use the squaring a binomial pattern to obtain
\(2x+3 = (3)^2−2(3)(\sqrt{2x})+(\sqrt{2x})^2\)
\(2x+3 = 9−6\sqrt{2x}+2x\).
We still have one radical expression left on the right-hand side of this equation, so we’ll follow the mantra “isolate the radical.” First, subtract 2x from both sides of the equation to obtain
\(3=9−6\sqrt{2x}\),
then subtract 9 from both sides of the equation.
\(−6=−6\sqrt{2x}\),
We’ve succeeded in isolating the radical term on one side of the equation. Now, divide both sides of the equation by −6, then square both sides of the resulting equation.
\(1 = \sqrt{2x}\)
\((1)^2 = (\sqrt{2x})^2\)
\(1 = 2x\)
Divide both sides of the last result by 2.
\(x = \frac{1}{2}\)
Note that this agrees nicely with our graphical solution (\(x \approx 0.5\)), but let’s check our solution by substituting \(x = \frac{1}{2}\) into the original equation.
\(\sqrt{2x}+\sqrt{2x+3} = 3\)
\(\sqrt{2(\frac{1}{2})}+\sqrt{2(\frac{1}{2})+3} = 3\)
\(\sqrt{1}+\sqrt{4} = 3\)
1+2 = 3
This last statement is true, so the solution \(x = \frac{1}{2}\) checks.
Exercise
For the rational functions in Exercises 1-6, perform each of the following tasks.
- Load the function f and the line y = k into your graphing calculator. Adjust the viewing window so that all point(s) of intersection of the two graphs are visible in your viewing window.
- Copy the image in your viewing window onto your homework paper. Label and scale each axis with xmin, xmax, ymin, and ymax. Label the graphs with their equations. Remember to draw all lines with a ruler.
- Use the intersect utility to determine the coordinates of the point(s) of intersection. Plot the point of intersection on your homework paper and label it with its coordinates.
- Solve the equation f(x) = k algebraically. Place your work and solution next to your graph. Do the solutions agree?
\(f(x) = \sqrt{4−x}\), k = 3
\(f(x) = \sqrt{3x+5}\), k = 5
\(f(x) = \sqrt{4−x}\), k = 5
In Exercises 7-12, use an algebraic technique to solve the given equation. Check your solutions.
\(\sqrt{−5x+5} = 2\)
- Answer
-
\(\frac{1}{5}\)
\(\sqrt{4x+6} = 7\)
\(\sqrt{6x−8} = 8\)
- Answer
-
12
\(\sqrt{2x+4} = 2\)
\(\sqrt{−3x+1} = 3\)
- Answer
-
\(x = −\frac{8}{3}\)
\(\sqrt{4x+7} = 3\)
For the rational functions in Exercises 13-16 perform each of the following tasks.
- Load the function f and the line y = k into your graphing calculator. Adjust the viewing window so that all point(s) of intersection of the two graphs are visible in your viewing window.
- Copy the image in your viewing window onto your homework paper. Label and scale each axis with xmin, xmax, ymin, and ymax. Label the graphs with their equations. Remember to draw all lines with a ruler.
- Use the intersect utility to determine the coordinates of the point(s) of intersection. Plot the point of intersection on your homework paper and label it with its coordinates.
- Solve the equation f(x) = k algebraically. Place your work and solution next to your graph. Do the solutions agree?
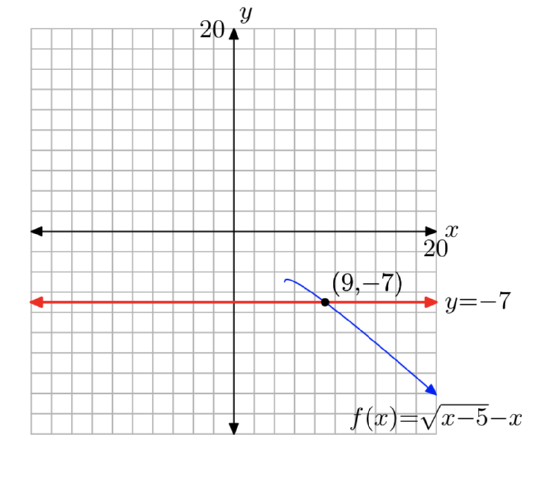
\(f(x) = \sqrt{x+6}−x\), k = 4
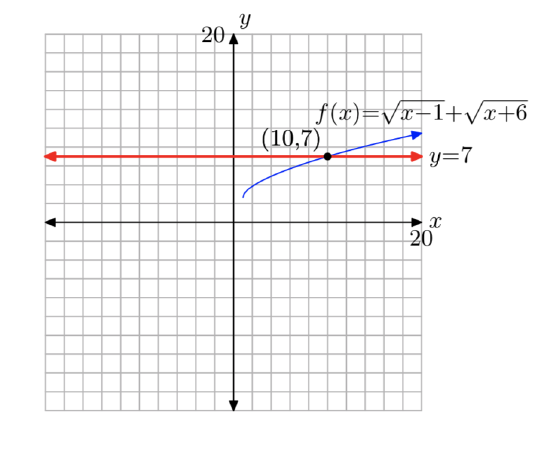
\(f(x) = \sqrt{x+5}+x\), k = 7
In Exercise17-24, use an algebraic technique to solve the given equation. Check your solutions.
\(\sqrt{x+1}+x = 5\)
- Answer
-
3
\(\sqrt{x+8}−x = 8\)
\(\sqrt{x+4}+x = 8\)
- Answer
-
5
\(\sqrt{x+8}−x = 2\)
\(\sqrt{x+5}−x = 3\)
- Answer
-
−1
\(\sqrt{x+5}+x = 7\)
\(\sqrt{x+9}−x = 9\)
- Answer
-
−8, −9
\(\sqrt{x+7}+x = 5\)
For the rational functions in Exercises 25-28, perform each of the following tasks.
- Load the function f and the line y =k into your graphing calculator. Adjust the viewing window so that all point(s) of intersection of the two graphs are visible in your viewing window.
- Copy the image in your viewing window onto your homework paper. Label and scale each axis with xmin, xmax, ymin, and ymax. Label the graphs with their equations. Remember to draw all lines with a ruler.
- Use the intersect utility to determine the coordinates of the point(s) of intersection. Plot the point of intersection on your homework paper and label it with its coordinates.
- Solve the equation f(x) = k algebraically. Place your work and solution next to your graph. Do the solutions agree?
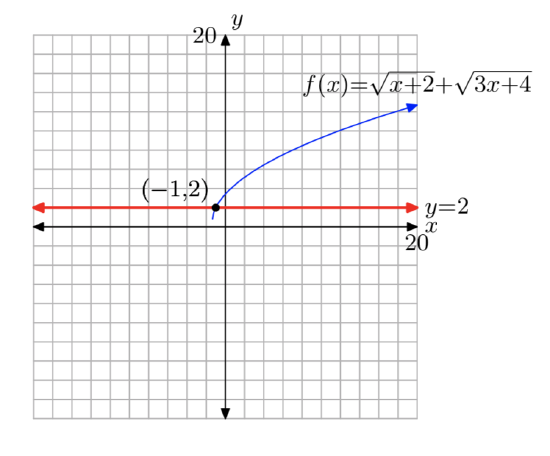
\(f(x) = \sqrt{x+2}+\sqrt{x+9}, k = 7\)
\(f(x)= \sqrt{6x+7}+\sqrt{3x+3}, k = 1\)
In Exercises 29-40, use an algebraic technique to solve the given equation. Check your solutions.
\(\sqrt{x+46}−\sqrt{x−35} = 1\)
- Answer
-
1635
\(\sqrt{x−16}+\sqrt{x+16} = 8\)
\(\sqrt{x−19}+\sqrt{x−6} = 13\)
- Answer
-
55
\(\sqrt{x+31}−\sqrt{x+12} = 1\)
\(\sqrt{x−2}−\sqrt{x−49} = 1\)
- Answer
-
578
\(\sqrt{x+13}+\sqrt{x+8} = 5\)
\(\sqrt{x+27}−\sqrt{x−22} = 1\)
- Answer
-
598
\(\sqrt{x+10}+\sqrt{x+13} = 3\)
\(\sqrt{x+30}−\sqrt{x−38} = 2\)
- Answer
-
294
\(\sqrt{x+36}−\sqrt{x+11} = 1\)
\(\sqrt{x−17}+\sqrt{x+3} = 10\)
- Answer
-
33
\(\sqrt{x+18}+\sqrt{x+13} = 5\)