9.3: Division Properties of Radicals

Each of the equations \(x^2 = a\) and \(x^2 = b\) has a unique positive solution, \(x = \sqrt{a}\) and \(x =\sqrt{b}\), respectively, provided \(a\) and \(b\) are positive real numbers. Further, because they are solutions, they can be substituted into the equations \(x^2 = a\) and \(x^2 = b\) to produce the results

\((\sqrt{a})^2 = a\) and \((\sqrt{b})^2 =b\),

respectively. These results are dependent upon the fact that a and b are positive real numbers.

Similarly, the equation

\[x^2 = \frac{a}{b} \nonumber \]

has the unique positive solution

\[x = \sqrt{\frac{a}{b}} \nonumber \]

provided \(a\) and \(b\) are positive real numbers. However, note that

\[\left(\frac{\sqrt{a}}{\sqrt{b}}\right)^2 = \frac{(\sqrt{a})^2}{(\sqrt{b})^2} = \frac{a}{b}, \nonumber \]

making \(\frac{\sqrt{a}}{\sqrt{b}}\) a second positive solution of \(x^2 = \frac{a}{b}\). However, because \(\sqrt{\frac{a}{b}}\) is the unique positive solution of \(x^2 = \frac{a}{b}\), this forces

\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \nonumber \]

This discussion leads us to the following property of radicals.

Property 1

Let \(a\) and \(b\) be positive real numbers. Then,

\[\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \nonumber \]

This result can be used in two distinctly different ways.

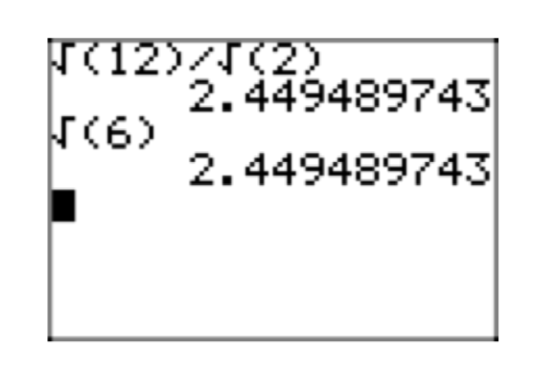
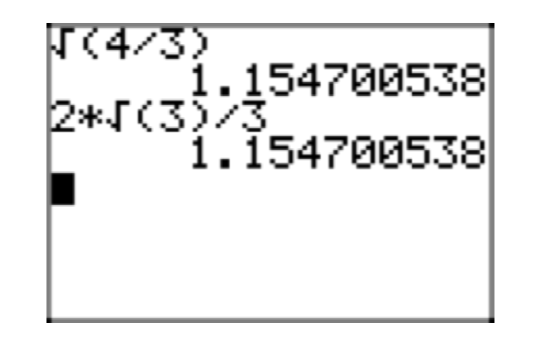
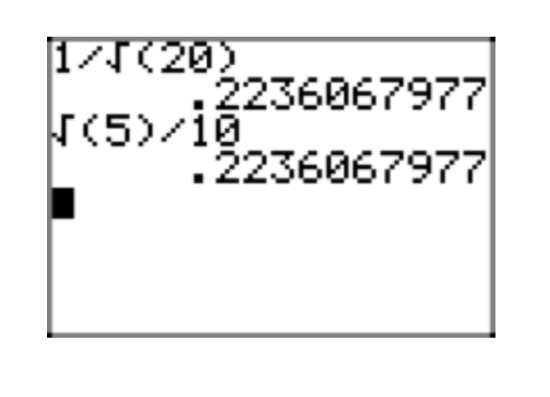
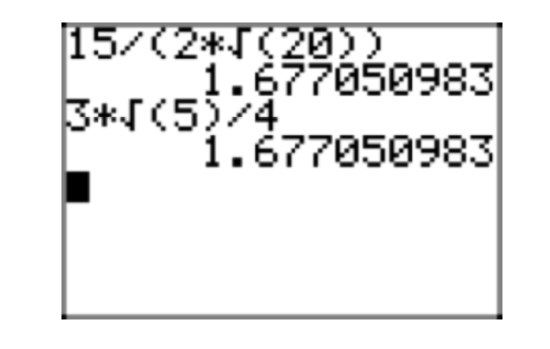
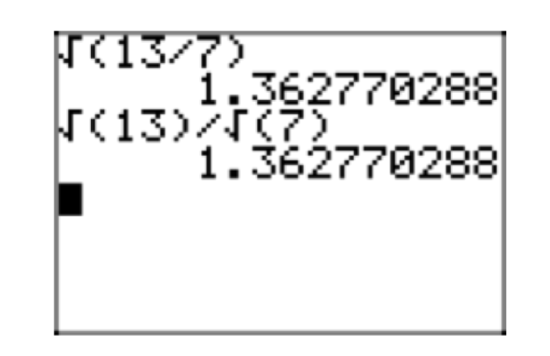
• You can use the result to divide two square roots, as in \[\frac{\sqrt{13}}{\sqrt{7}} = \sqrt{\frac{13}{7}} \nonumber \]
• You can also use the result to take the square root of a fraction. Simply take the square root of both numerator and denominator, as in \[\sqrt{\frac{13}{7}} = \frac{\sqrt{13}}{\sqrt{7}} \nonumber \]

It is interesting to check these results on a calculator, as shown in Figure 1.

Figure 1. Checking that \(\sqrt{\frac{13}{7}} = \frac{\sqrt{13}}{\sqrt{7}}\)

Simple Radical Form Continued

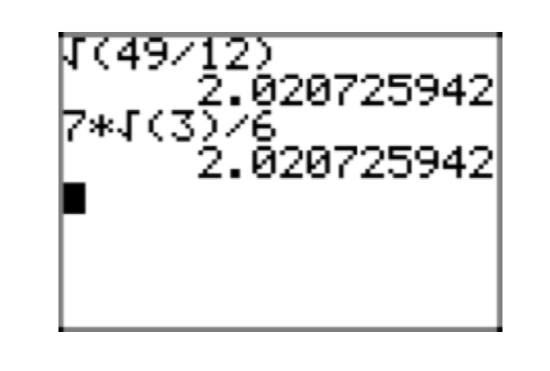
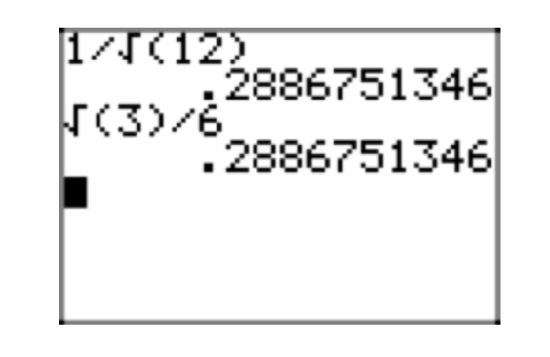
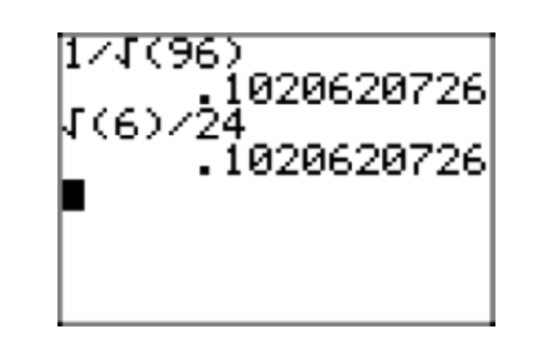
David and Martha are again working on a homework problem. Martha obtains the solution \(\sqrt{\frac{1}{12}}\), but David’s solution \(\frac{1}{(2\sqrt{3})}\) is seemingly different. Having learned their lesson in an earlier assignment, they use their calculators to find decimal approximations of their solutions. Martha’s approximation is shown in Figure 2(a) and David’s approximation is shown in Figure 2(b).

Figure 2. Comparing Martha’s \(\sqrt{\frac{1}{12}}\) with David's \(\frac{1}{(2\sqrt{3})}\)

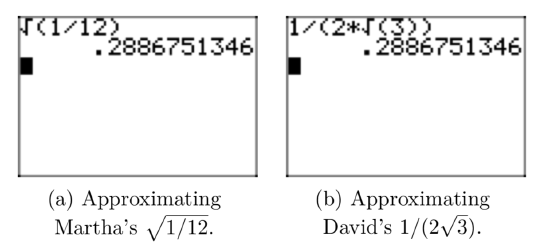
Martha finds that \(\sqrt{\frac{1}{12}} \approx 0.2886751346\) and David finds that \(\frac{1}{(2\sqrt{3})} \approx 0.2886751346\). They conclude that their answers match, but they want to know why such different looking answers are identical.

The following calculation shows why Martha’s result is identical to David’s. First, use the division property of radicals (Property 1) to take the square root of both numerator and denominator.

\[\sqrt{\frac{1}{12}} = \frac{\sqrt{1}}{\sqrt{12}} = \frac{1}{\sqrt{12}} \nonumber \]

Next, use the “first guideline for simple radical form” and factor a perfect square from the denominator.

\[\frac{1}{\sqrt{12}} = \frac{1}{\sqrt{4}\sqrt{3}} = \frac{1}{2\sqrt{3}} \nonumber \]

This clearly demonstrates that David and Martha’s solutions are identical.

Indeed, there are other possible forms for the solution of David and Martha’s home- work exercise. Start with Martha’s solution, then multiply both numerator and de- nominator of the fraction under the radical by 3.

\[\sqrt{\frac{1}{12}} = \sqrt{\frac{1}{12} \cdot \frac{3}{3}} = \sqrt{\frac{3}{36}} \nonumber \]

Now, use the division property of radicals (Property 1), taking the square root of both numerator and denominator.

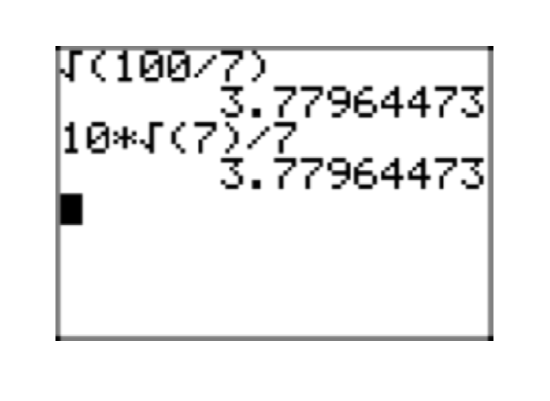
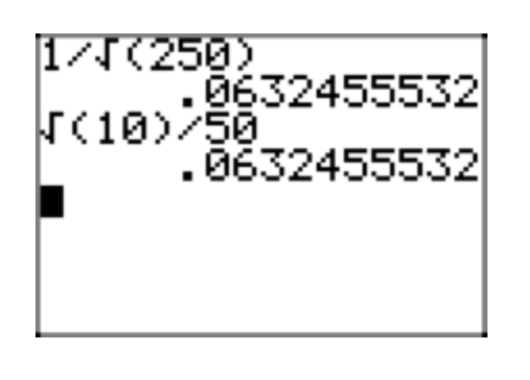
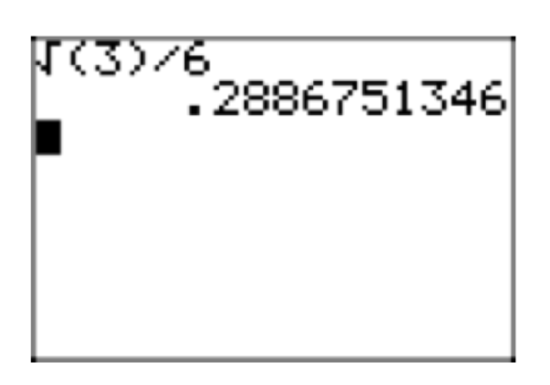
\[\sqrt{\frac{3}{36}} = \frac{\sqrt{3}}{\sqrt{36}} = \frac{\sqrt{3}}{6} \nonumber \]

Note that the approximation of approximations of \(\frac{\sqrt{3}}{6}\) in Figure 3 is identical to Martha’s and David’s approximations in Figures 2(a) and (b).

Figure 3. Finding an approximation of \(\frac{\sqrt{3}}{6}\)

While all three of the solution forms (\(\sqrt{\frac{1}{12}}\), \(\frac{1}{(2\sqrt{3})}\), and \(\frac{\sqrt{3}}{6}\)) are identical, it is very frustrating to have so many forms, particularly when we want to compare solutions. So, we are led to establish two more guidelines for simple radical form.

The Second Guideline for Simple Radical Form

Do not leave fractions under a radical.

Thus, Martha’s \(\sqrt{\frac{1}{12}}\) is not in simple radical form, because it contains a fraction under the radical.

The Third Guideline for Simple Radical Form

Don’t leave radicals in the denominator of a fraction.

Thus, David’s \(\frac{1}{(2\sqrt{3})}\) is not in simple radical form, because the denominator of his fraction contains a radical.

Only the equivalent form \(\frac{\sqrt{3}}{6}\) obeys all three rules of simple radical form.

1. It is not possible to factor a perfect square from any radical in the expression \(\frac{\sqrt{3}}{6}\).
2. There are no fractions under a radical in the expression \(\frac{\sqrt{3}}{6}\).
3. The denominator in the expression \(\frac{\sqrt{3}}{6}\) contains no radicals.

In this text and in this course, we will always follow the three guidelines for simple radical form.

Simple Radical Form

When your answer is a radical expression:

1. If possible, factor out a perfect square.
2. Don’t leave fractions under a radical.
3. Don’t leave radicals in the denominator of a fraction.

In the examples that follow (and in the exercises), it is helpful if you know the squares of the first 25 positive integers. We’ve listed them in the margin for you in Table 1 for future reference.

Let’s place a few radical expressions in simple radical form. We’ll start with some radical expressions that contain fractions under a radical.

Example \(\PageIndex{2}\)

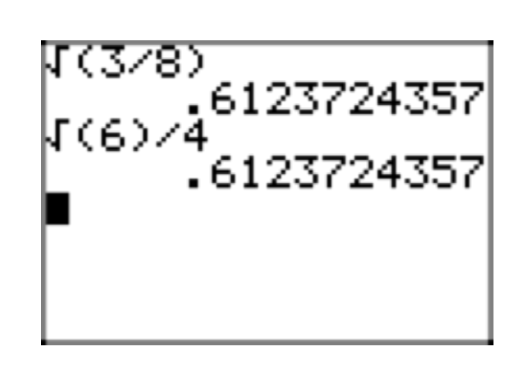
Place the expression \(\sqrt{\frac{1}{8}}\) in simple radical form.

Solution

The expression \(\sqrt{\frac{1}{8}}\) contains a fraction under a radical. We could take the square root of both numerator and denominator, but that would produce \(\frac{\sqrt{1}}{\sqrt{8}}\), which puts a radical in the denominator.

The better strategy is to change the form of \(\frac{1}{8}\) so that we have a perfect square in the denominator before taking the square root of the numerator and denominator. We note that if we multiply 8 by 2, the result is 16, a perfect square. This is hopeful, so we begin the simplification by multiplying both numerator and denominator of \(\frac{1}{8}\) by 2.

\(\sqrt{\frac{1}{8}} = \sqrt{\frac{1}{8} \cdot \frac{2}{2}} = \sqrt{\frac{2}{16}}\)

We now take the square root of both numerator and denominator. Because the denominator is now a perfect square, the result will not have a radical in the denominator.

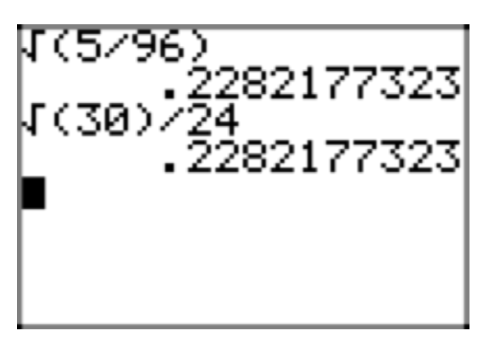
\(\sqrt{\frac{2}{16}} = \frac{\sqrt{2}}{\sqrt{16}} = \frac{\sqrt{2}}{4}\)

This last result, \(\frac{\sqrt{2}}{4}\) is in simple radical form. It is not possible to factor a perfect square from any radical, there are no fractions under any radical, and the denominator is free of radicals.

You can easily check your solution by using your calculator to compare the original expression with your simple radical form. In Figure 4(a), we’ve approximated the original expression, \(\sqrt{\frac{1}{8}}\). In Figure 4(b), we’ve approximated our simple radical form \(\frac{\sqrt{2}}{4}\). Note that they yield identical decimal approximations.

Figure 4. Comparing \(\sqrt{\frac{1}{8}}\) and \(\frac{\sqrt{2}}{4}\)

Let’s look at another example.

Example \(\PageIndex{3}\)

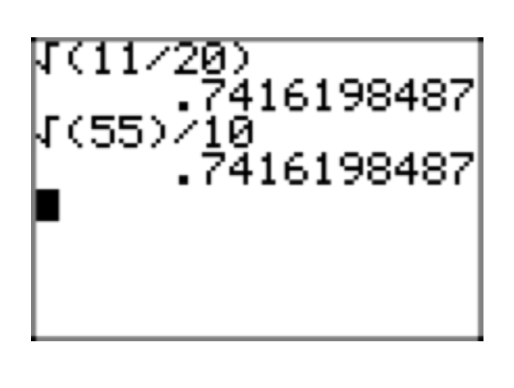
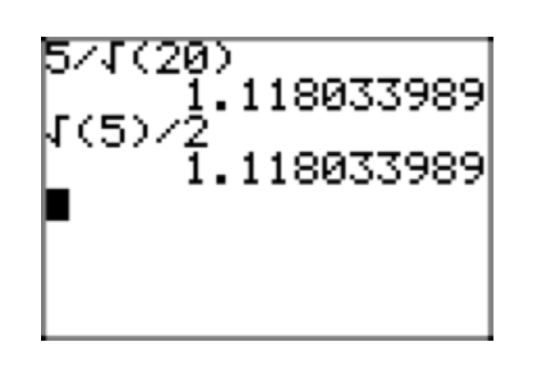
Place \(\sqrt{\frac{3}{20}}\) in simple radical form.

Solution

Following the lead from Example 2, we note that \(5 \cdot 20 = 100\), a perfect square. So, we multiply both numerator and denominator by 5, then take the square root of both numerator and denominator once we have a perfect square in the denominator.

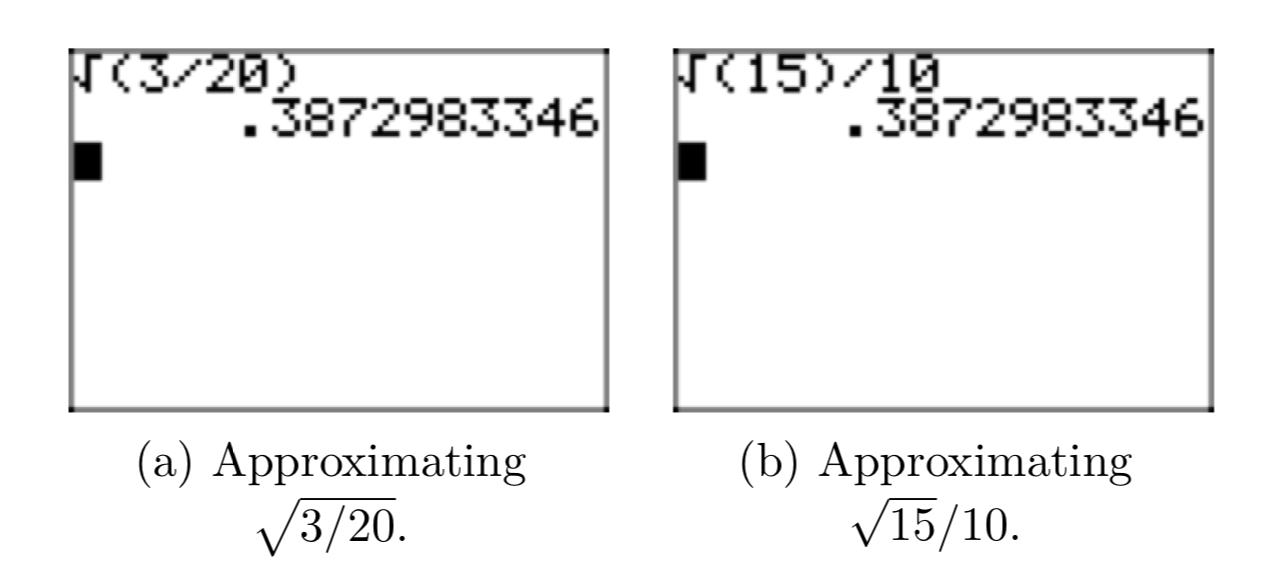
\(\sqrt{\frac{3}{20}} = \sqrt{\frac{3}{20} \cdot \frac{5}{5}} = \sqrt{\frac{15}{100}} = \frac{\sqrt{15}}{\sqrt{100}} = \frac{\sqrt{15}}{10}\)

Note that the decimal approximation of the simple radical form \(\frac{\sqrt{15}}{10}\) in Figure 5(b) matches the decimal approximation of the original expression \(\frac{3}{20}\) in Figure 5(a).

Figure 5. Comparing the original \(\sqrt{\frac{3}{20}}\) with the simple radical form \(\frac{\sqrt{15}}{10}\)

We will now show how to deal with an expression having a radical in its denominator, but first we pause to explain a new piece of terminology.

Rationalizing the Denominator

The process of eliminating radicals from the denominator is called rationalizing the denominator because it results in a fraction where the denominator is free of radicals and is a rational number.

Exercise \(\PageIndex{4}\)

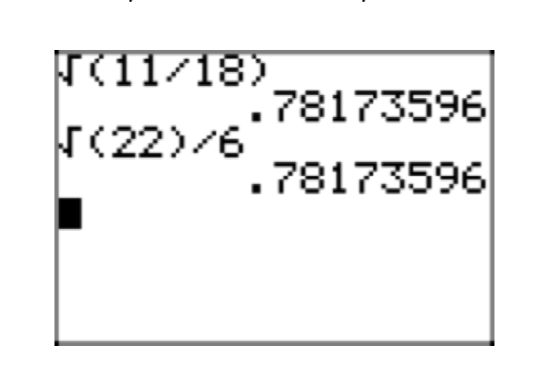
Place the expression \(\frac{5}{\sqrt{18}}\) in simple radical form.

Solution

In the previous examples, making the denominator a perfect square seemed a good tactic. We apply the same tactic in this example, noting that \(2 \cdot 18 = 36\) is a perfect square. However, the strategy is slightly different, as we begin the solution by multiplying both numerator and denominator by \(\sqrt{2}\).

\[\frac{5}{\sqrt{18}} = \frac{5}{\sqrt{18}} \cdot \frac{\sqrt{2}}{\sqrt{2}} \nonumber \]

We now multiply numerators and denominators. In the denominator, the multiplication property of radicals is used, \(\sqrt{18}\sqrt{2} = \sqrt{36}\).

\[\frac{5}{\sqrt{18}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{5\sqrt{2}}{\sqrt{36}} \nonumber \]

The strategy should now be clear. Because the denominator is a perfect square, \(\sqrt{36} = 6\), clearing all radicals from the denominator of our result.

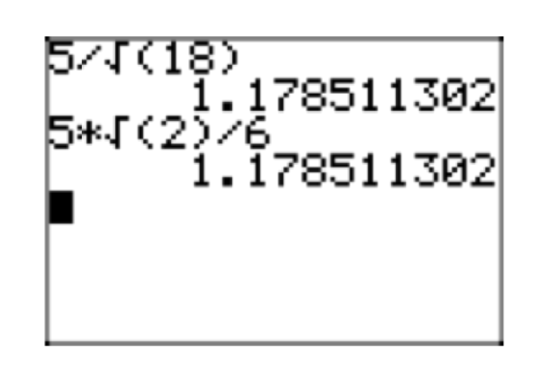
\[\frac{5\sqrt{2}}{\sqrt{36}} = \frac{5\sqrt{2}}{6} \nonumber \]

The last result is in simple radical form. It is not possible to extract a perfect square root from any radical, there are no fractions under any radical, and the denominator is free of radicals.

In Figure 6, we compare the approximation for our original expression with \(\frac{5}{\sqrt{18}}\) our simple radical form \(\frac{5\sqrt{2}}{6}\).

Figure 6. Comparing \(\frac{5}{\sqrt{18}}\) with \(\frac{5\sqrt{2}}{6}\)

Let’s look at another example.

Example \(\PageIndex{5}\)

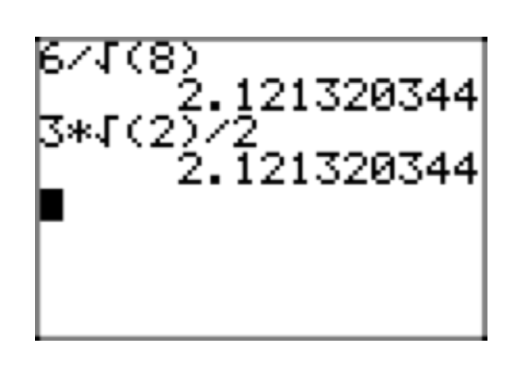
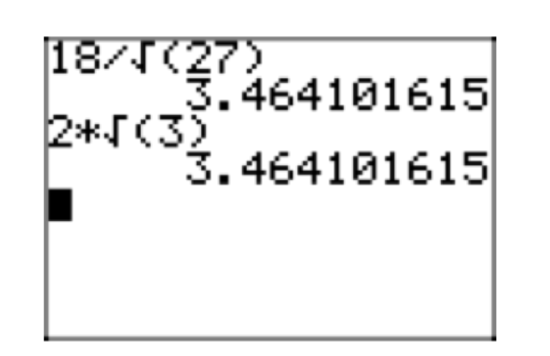
Place the expression \(\frac{18}{\sqrt{27}}\) in simple radical form.

Solution

Note that \(3 \cdot 27 = 81\) is a perfect square. We begin by multiplying both numerator and denominator of our expression \(\sqrt{3}\).

\(\frac{18}{\sqrt{27}} = \frac{18}{\sqrt{27}} \cdot \frac{\sqrt{3}}{\sqrt{3}}\)

Multiply numerators and denominators. In the denominators, \(\sqrt{27}\sqrt{3} = \sqrt{81}\)

\(\frac{18}{\sqrt{27}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{18\sqrt{3}}{\sqrt{81}}\)

Of course, \(\sqrt{81} = 9\), so

\(\frac{18\sqrt{3}}{\sqrt{81}} = \frac{18\sqrt{3}}{9}\)

We can now reduce to lowest terms, dividing numerator and denominator by 9.

\(\frac{18\sqrt{3}}{9} = 2\sqrt{3}\)

In Figure 7, we compare approximations of the original expression \(\frac{18}{\sqrt{27}}\) and its simple radical form \(2\sqrt{3}\).

Figure 7. Comparing \(\frac{18}{\sqrt{27}}\) with its simple radical form \(2\sqrt{3}\).

Helpful Hints

In the previous section, we learned that if you square a product of exponential expressions, you multiply each of the exponents by 2.

\((2^{3}3^{4}5^{5})^2 = 2^{6}3^{8}5^{10}\)

Because taking the square root is the “inverse” of squaring, we divide each of the exponents by 2.

\(\sqrt{2^{6}3^{8}5^{10}} = 2^{3}3^{4}5^{5}\)

We also learned that prime factorization is an extremely powerful tool that is quite useful when placing radical expressions in simple radical form. We’ll see that this is even more true in this section.

Let’s look at an example.

Example \(\PageIndex{6}\)

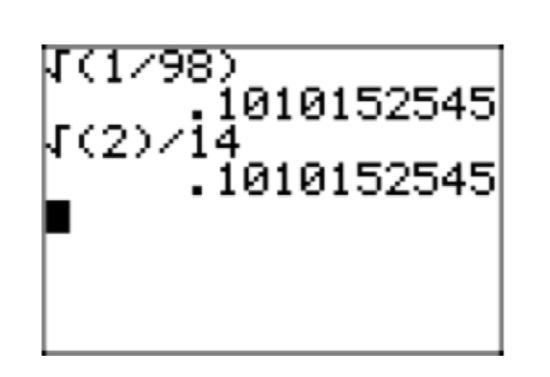
Place the expression \(\sqrt{\frac{1}{98}}\) in simple radical form.

Solution

Sometimes it is not easy to figure out how to scale the denominator to get a perfect square, even when provided with a table of perfect squares. This is when prime factorization can come to the rescue and provide a hint. So, first express the denominator as a product of primes in exponential form: \(98 = 2 \cdot 49 = 2 \cdot 7^2\)

\(\sqrt{\frac{1}{98}} = \sqrt{\frac{1}{2 \cdot 7^2}}\)

We can now easily see what is preventing the denominator from being a perfect square. The problem is the fact that not all of the exponents in the denominator are divisible by 2. We can remedy this by multiplying both numerator and denominator by 2.

\(\sqrt{\frac{1}{2 \cdot 7^2}} = \sqrt{\frac{1}{2 \cdot 7^2} \cdot \frac{2}{2}} = \sqrt{\frac{2}{2^{2}7^{2}}}\)

Note that each prime in the denominator now has an exponent that is divisible by 2. We can now take the square root of both numerator and denominator.

\(\sqrt{\frac{2}{2^{2}7^{2}}} = \frac{\sqrt{2}}{\sqrt{2^{2}7^{2}}}\)

Take the square root of the denominator by dividing each exponent by 2.

\(\frac{\sqrt{2}}{\sqrt{2^{2}7^{2}}} = \frac{\sqrt{2}}{2^{1} \cdot 7^{1}}\)

Then, of course, \(2 \cdot 7 = 14\).

\(\frac{\sqrt{2}}{2 \cdot 7} = \frac{\sqrt{2}}{14}\)

In Figure 8, note how the decimal approximations of the original expression \(\sqrt{\frac{1}{98}}\) and its simple radical form \(\frac{\sqrt{2}}{14}\) match, strong evidence that we've found the correct simple radical form. That is, we cannot take a perfect square out of any radical, there are no fractions under any radical, and the denominators are clear of all radicals.

Figure 8. Comparing the original \(\sqrt{\frac{1}{98}}\) with its simple radical form \(\frac{\sqrt{2}}{14}\)

Let’s look at another example.

Example \(\PageIndex{7}\)

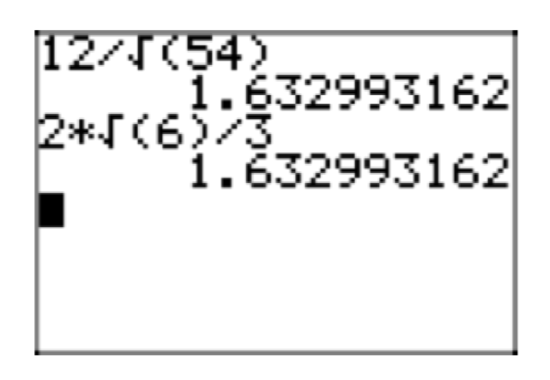
Place the expression \(\frac{12}{\sqrt{54}}\) in simple radical form.

Solution

Prime factor the denominator: \( 54 = 2 \cdot 27 = 2 \cdot 3^3\).

\(\frac{12}{\sqrt{54}} = \frac{12}{\sqrt{2 \cdot 3^3}}\)

Neither prime in the denominator has an exponent divisible by 2. If we had another 2 and one more 3, then the exponents would be divisible by 2. This encourages us to multiply both numerator and denominator by \(\sqrt{2 \cdot 3}\).

\(\frac{12}{\sqrt{2 \cdot 3^3}} = \frac{12}{\sqrt{2 \cdot 3^3}} \cdot \frac{\sqrt{2 \cdot 3}}{\sqrt{2 \cdot 3}} = \frac{12\sqrt{2 \cdot 3}}{\sqrt{2^{2}3^4}}\)

Divide each of the exponents in the denominator by 2.

\(\frac{12\sqrt{2 \cdot 3}}{\sqrt{2^{2}3^4}} = \frac{12\sqrt{2 \cdot 3}}{2^{1} \cdot 3^2}\)

Then, in the numerator, \(2 \cdot 3 = 6\), and in the denominator, \(2 \cdot 3^2 = 18\).

\(\frac{12\sqrt{2 \cdot 3}}{2 \cdot 3^{2}} = \frac{12\sqrt{6}}{18}\)

Finally, reduce to lowest terms by dividing both numerator and denominator by 6.

\(\frac{12\sqrt{6}}{18} = \frac{2\sqrt{6}}{3}\)

In Figure 9, the approximation for the original expression \(\frac{12}{\sqrt{54}}\) matches that of its simple radical form \(\frac{2\sqrt{6}}{3}\)

Figure 9. Comparing the original \(\frac{12}{\sqrt{54}}\) with its simple radical form \(\frac{2\sqrt{6}}{3}\)

Variable Expressions

If x is any real number, recall again that

\[\sqrt{x^2} = |x| \nonumber \]

If we combine the law of exponents for squaring a quotient with our property for taking the square root of a quotient, we can write

\[\sqrt{(\frac{a}{b})^2} = \sqrt{\frac{a^2}{b^2}} = \frac{\sqrt{a^2}}{\sqrt{b^2}} \nonumber \]

However, \(\sqrt{(\frac{a}{b})^2} = |\frac{a}{b}|\), while \(\frac{\sqrt{a^2}}{\sqrt{b^2}} = \frac{|a|}{|b|}\). This discussion leads to the following key result.

Quotient Rule for Absolute Value

If a and b are any real numbers, then

\[\left|\dfrac{a}{b}\right| = \frac{|a|}{|b|} \nonumber \]

provided \(b \ne 0\). In words, the absolute value of a quotient is the quotient of the absolute values.

We saw this property previously in the chapter on the absolute value function, where we provided a different approach to the proof of the property. It’s interesting that we can prove this property in a completely new way using the properties of square root. We’ll see we have need for the Quotient Rule for Absolute Value in the examples that follow.

For example, if x is any real number except zero, using the quotient rule for absolute value we could write

\[\left|\dfrac{3}{x}\right| = \frac{|3|}{|x|} = \frac{3}{|x|}\nonumber \]

However, there is no way to remove the absolute value bars that surround x unless we know the sign of x. If x > 0 (remember, no zeros in the denominator), then |x| = x and the expression becomes

\[\frac{3}{|x|} = \frac{3}{x} \nonumber \]

On the other hand, if x < 0, then |x| = −x and the expression becomes

\[\frac{3}{|x|} = \frac{3}{−x} = −\frac{3}{x} \nonumber \]

Let’s look at another example.

Example \(\PageIndex{8}\)

Place the expression \(\sqrt{\frac{18}{x^6}}\) in simple radical form. Discuss the domain.

Solution

Note that x cannot equal zero, otherwise the denominator of \(\sqrt{\frac{18}{x^6}}\) would be zero, which is not allowed. However, whether x is positive or negative, \(x^6\) will be a positive number (raising a nonzero number to an even power always produces a positive real number), and \(\sqrt{\frac{18}{x^6}}\) is well-defined.

Keeping in mind that x is nonzero, but could either be positive or negative, we proceed by first invoking Property 1, taking the positive square root of both numerator and denominator of our radical expression.

\[\sqrt{\frac{18}{x^6}} = \frac{\sqrt{18}}{\sqrt{x^6}} \nonumber \]

From the numerator, we factor a perfect square. In the denominator, we use absolute value bars to insure a positive square root.

\(\frac{\sqrt{18}}{\sqrt{x^6}} = \frac{\sqrt{9}\sqrt{2}}{|x^3|} = \frac{3\sqrt{2}}{|x^3|}\)

We can use the Product Rule for Absolute Value to write \(|x^3| = |x^2||x| = x^{2}|x|\). Note that we do not need to wrap \(x^2\) in absolute value bars because \(x^2\) is already positive.

\[\frac{3\sqrt{2}}{|x^3|} = \frac{3\sqrt{2}}{x^{2}|x|} \nonumber \]

Because x could be positive or negative, we cannot remove the absolute value bars around x. We are done.

Let’s look at another example.

Example \(\PageIndex{9}\)

Place the expression \(\sqrt{\frac{12}{x^5}}\) in simple radical form. Discuss the domain.

Solution

Note that x cannot equal zero, otherwise the denominator of \(\sqrt{\frac{12}{x^5}}\) would be zero, which is not allowed. Further, if x is a negative number, then \(x^5\) will also be a negative number (raising a negative number to an odd power produces a negative number). If x were negative, then \(\frac{12}{x^5}\) would also be negative and \(\sqrt{\frac{12}{x^5}}\) would be undefined (you cannot take the square root of a negative number). Thus, x must be a positive real number or the expression \(\sqrt{\frac{12}{x^5}}\) is undefined.

We proceed, keeping in mind that \(x\) is a positive real number. One possible approach is to first note that another factor of x is needed to make the denominator a perfect square. This motivates us to multiply both numerator and denominator inside the radical by \(x\).

\[\sqrt{\frac{12}{x^5}} = \sqrt{\frac{12}{x^5} \cdot \frac{x}{x}} = \sqrt{\frac{12x}{x^6}} \nonumber \]

We can now use Property 1 to take the square root of both numerator and denominator.

\[\sqrt{\frac{12x}{x^6}} = \frac{\sqrt{12x}}{\sqrt{x^6}} \nonumber \]

In the numerator, we factor out a perfect square. In the denominator, absolute value bars would insure a positive square root. However, we’ve stated that x must be a positive number, so \(x^3\) is already positive and absolute value bars are not needed.

\[\frac{\sqrt{12x}}{\sqrt{x^6}} = \frac{\sqrt{4}\sqrt{3x}}{x^3} = \frac{2\sqrt{3x}}{x^3} \nonumber \]

Let’s look at another example.

Example \(\PageIndex{10}\)

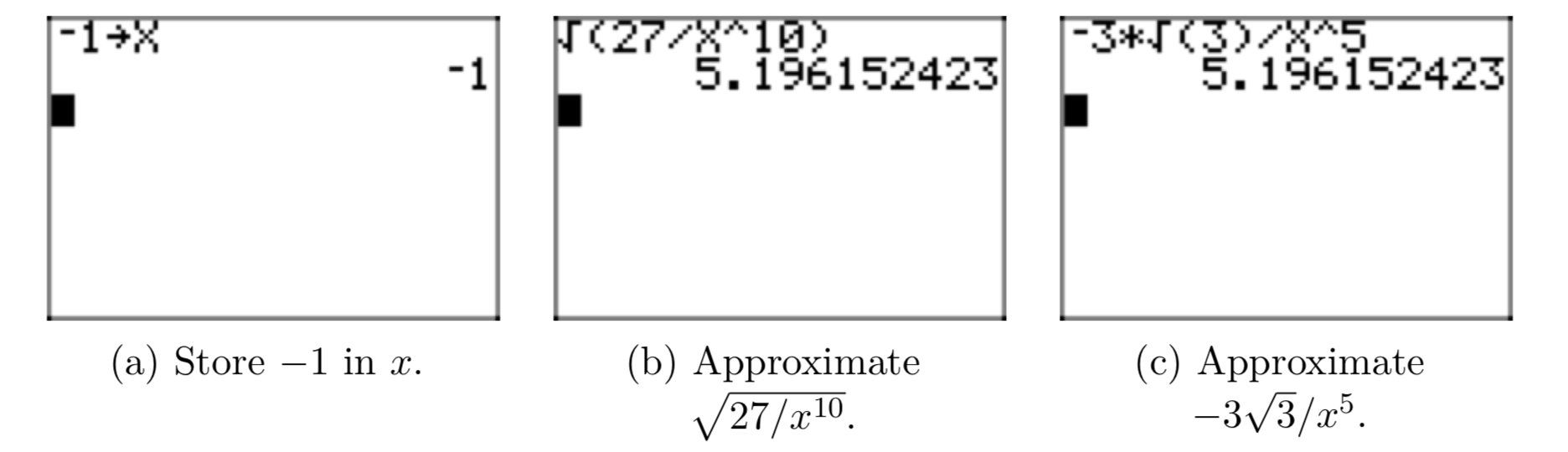
Given that x < 0, place \(\sqrt{\frac{27}{x^{10}}}\) in simple radical form.

Solution

One possible approach would be to factor out a perfect square and write

\[\sqrt{\frac{27}{x^{10}}} = \sqrt{\frac{9}{x^{10}} \cdot \sqrt{3}} = \sqrt{(\frac{3}{x^5})^2}\sqrt{3} = |\frac{3}{x^5}|\sqrt{3}. \nonumber \]

Now, \(|\frac{3}{x^5}| = \frac{|3|}{(|x^4||x|} = \frac{3}{x^{4}|x|}\), since \(x^4 > 0\). Thus,

\[|\frac{3}{x^5}|\sqrt{3} = \frac{3}{x^{4}|4|}\sqrt{3}. \nonumber \]

However, we are given that x < 0, so |x| = −x and we can write

\[\frac{3}{x^{4}|x|}\sqrt{3} = \frac{3}{x^{4}|x|}\sqrt{3} = \frac{3}{x^{4}(−x)}\sqrt{3} = −\frac{3}{x^5}\sqrt{3} \nonumber \]

We can move \(\sqrt{3}\) into the numerator and write

\[−\frac{3}{x^5}\sqrt{3} = −\frac{3\sqrt{3}}{x^5}. \nonumber \]

Again, it’s instructive to test the validity of this result using your graphing calculator. Supposedly, the result is true for all values of x < 0. So, store −1 in x, then enter the original expression and its simple radical form, then compare the approximations, as shown in Figures 10(a), (b), and (c).

Figure 10. Comparing the original expression and its simple radical form at x = −1.

Alternative approach. A slightly different approach would again begin by taking the square root of both numerator and denominator.

\(\sqrt{\frac{27}{x^{10}}} = \frac{\sqrt{27}}{\sqrt{x^{10}}}\)

Now, \(\sqrt{27} = \sqrt{9}\sqrt{3} = 3\sqrt{3}\) and we insure that \(\sqrt{x^{10}}\) produces a positive number by using absolute value bars. That is, \(\sqrt{x^{10}} = |x^5|\) and

\(\frac{\sqrt{27}}{\sqrt{x^{10}}} = \frac{3\sqrt{3}}{|x^5|}\)

However, using the product rule for absolute value and the fact that \(x^4 > 0\), \(|x^5| =|x^4||x| = x^{4}|x|\) and

\(\frac{3\sqrt{3}}{|x^5|} = \frac{3\sqrt{3}}{x^{4}|x|}\)

Finally, we are given that x < 0, so |x| = −x and we can write

\(\frac{3\sqrt{3}}{x^{4}|x|} = \frac{3\sqrt{3}}{x^{4}(−x)} = −\frac{3\sqrt{3}}{x^5}\).

Exercise \(\PageIndex{11}\)

Use a calculator to first approximate \(\frac{\sqrt{5}}{\sqrt{2}}\). On the same screen, approximate \(\sqrt{\frac{5}{2}}\). Report the results on your homework paper.

Answer

Both \(\frac{\sqrt{5}}{\sqrt{2}} = \sqrt{\frac{5}{2}} \approx = 1.58113883\)

Exercise \(\PageIndex{2}\)

Use a calculator to first approximate \(\frac{\sqrt{7}}{\sqrt{5}}\). On the same screen, approximate \(\sqrt{\frac{7}{5}}\). Report the results on your homework paper.

Exercise \(\PageIndex{3}\)

Use a calculator to first approximate \(\frac{\sqrt{12}}{\sqrt{2}}\). On the same screen, approximate \(\sqrt{6}\). Report the results on your homework paper.

Answer

Both \(\frac{\sqrt{12}}{\sqrt{2}} = \sqrt{6} \approx 2.449489743\).

Exercise \(\PageIndex{4}\)

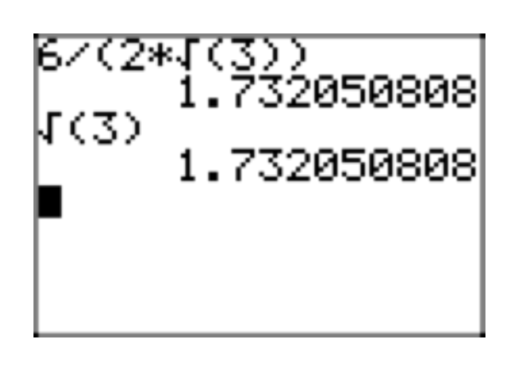
Use a calculator to first approximate \(\frac{\sqrt{15}}{\sqrt{5}}\). On the same screen, approximate \(\sqrt{3}\). Report the results on your homework paper.

In Exercises 5-16, place each radical expression in simple radical form. As in Example 2 in the narrative, check your result with your calculator.

Exercise \(\PageIndex{5}\)

\(\sqrt{\frac{3}{8}}\)

Answer

\(\sqrt{\frac{3}{8}} = \sqrt{\frac{3}{8} \cdot \frac{2}{2}} = \sqrt{\frac{6}{16}} = \frac{\sqrt{6}}{4}\)

Exercise \(\PageIndex{6}\)

\(\sqrt{\frac{5}{12}}\)

Exercise \(\PageIndex{7}\)

\(\sqrt{\frac{11}{20}}\)

Answer

\(\sqrt{\frac{11}{20}} = \sqrt{\frac{11}{20} \cdot \frac{5}{5}} = \sqrt{\frac{55}{100}} = \frac{\sqrt{55}}{10}\)

Exercise \(\PageIndex{8}\)

\(\sqrt{\frac{3}{2}}\)

Exercise \(\PageIndex{9}\)

\(\sqrt{\frac{11}{18}}\)

Answer

\(\sqrt{\frac{11}{18}} = \sqrt{\frac{11}{18} \cdot \frac{2}{2}} = \sqrt{\frac{22}{36}} = \frac{\sqrt{22}}{6}\)

Exercise \(\PageIndex{10}\)

\(\sqrt{\frac{7}{5}}\)

Exercise \(\PageIndex{11}\)

\(\sqrt{\frac{4}{3}}\)

Answer

\(\sqrt{\frac{4}{3}} = \sqrt{\frac{4}{3} \cdot \frac{3}{3}} = \sqrt{\frac{12}{9}} = \frac{\sqrt{3}\sqrt{4}}{3}\)

Exercise \(\PageIndex{12}\)

\(\sqrt{\frac{16}{5}}\)

Exercise \(\PageIndex{13}\)

\(\sqrt{\frac{49}{12}}\)

Answer

\(\sqrt{\frac{49}{12}} = \sqrt{\frac{49}{12} \cdot \frac{3}{3}} = \sqrt{\frac{49 \cdot 3}{36}} = \frac{\sqrt{49}\sqrt{3}}{6} = \frac{7\sqrt{3}}{6}\)

Exercise \(\PageIndex{14}\)

\(\sqrt{\frac{81}{20}}\)

Exercise \(\PageIndex{15}\)

\(\sqrt{\frac{100}{7}}\)

Answer

\(\sqrt{\frac{100}{7}} = \sqrt{\frac{100}{7} \cdot \frac{7}{7}} = \sqrt{\frac{100 \cdot 7}{49}} = \frac{\sqrt{100}\sqrt{7}}{7} = \frac{10\sqrt{7}}{7}\)

Exercise \(\PageIndex{16}\)

\(\sqrt{\frac{36}{5}}\)

In Exercises 17-28, place each radical expression in simple radical form. As in Example 4 in the narrative, check your result with your calculator.

Exercise \(\PageIndex{17}\)

\(\frac{1}{\sqrt{12}}\)

Answer

\(\frac{1}{\sqrt{12}} = \frac{1}{\sqrt{12}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{36}} = \frac{\sqrt{3}}{6}\)

Exercise \(\PageIndex{18}\)

\(\frac{1}{\sqrt{8}}\)

Exercise \(\PageIndex{19}\)

\(\frac{1}{\sqrt{20}}\)

Answer

\(\frac{1}{\sqrt{20}} = \frac{1}{\sqrt{20}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{\sqrt{100}} = \frac{\sqrt{5}}{10}\)

Exercise \(\PageIndex{20}\)

\(\frac{1}{\sqrt{27}}\)

Exercise \(\PageIndex{21}\)

\(\frac{6}{\sqrt{8}}\)

Answer

\(\frac{6}{\sqrt{8}} = \frac{6}{\sqrt{8}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{6\sqrt{2}}{\sqrt{16}} = \frac{6\sqrt{2}}{4} = \frac{3\sqrt{2}}{2}\)

Exercise \(\PageIndex{22}\)

\(\frac{4}{\sqrt{12}}\)

Exercise \(\PageIndex{23}\)

\(\frac{5}{\sqrt{20}}\)

Answer

\(\frac{5}{\sqrt{20}} = \frac{5}{\sqrt{20}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{5\sqrt{5}}{\sqrt{100}} = \frac{5\sqrt{5}}{10} = \frac{\sqrt{5}}{2}\)

Exercise \(\PageIndex{24}\)

\(\frac{9}{\sqrt{27}}\)

Exercise \(\PageIndex{25}\)

\(\frac{6}{2\sqrt{3}}\)

Answer

\(\frac{6}{2\sqrt{3}} = \frac{6}{2\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = \frac{6\sqrt{3}}{2\sqrt{9}} =\frac{6\sqrt{3}}{6} = \sqrt{3}\)

Exercise \(\PageIndex{26}\)

\(\frac{10}{3\sqrt{5}}\)

Exercise \(\PageIndex{27}\)

\(\frac{15}{2\sqrt{20}}\)

Answer

\(\frac{15}{2\sqrt{20}} = \frac{15}{2\sqrt{20}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{15\sqrt{5}}{2\sqrt{100}} = \frac{15\sqrt{5}}{20} = \frac{3\sqrt{5}}{4}\)

Exercise \(\PageIndex{28}\)

\(\frac{3}{2\sqrt{18}}\)

In Exercises 29-36, place the given radical expression in simple form. Use prime factorization as in Example 8 in the narrative to help you with the calculations. As in Example 6, check your result with your calculator.

Exercise \(\PageIndex{29}\)

\(\frac{1}{\sqrt{96}}\)

Answer

\(\frac{1}{\sqrt{96}} = \frac{1}{\sqrt{2^5 \cdot 3}} = \frac{1}{\sqrt{2^5 \cdot 3}} \cdot \frac{\sqrt{2 \cdot 3}}{\sqrt{2 \cdot 3}} = \frac{\sqrt{2 \cdot 3}}{2^6 \cdot 3^2} = \frac{\sqrt{2 \cdot 3}}{2^3 \cdot 3} = \frac{\sqrt{6}}{24}\)

Exercise \(\PageIndex{30}\)

\(\frac{1}{\sqrt{432}}\)

Exercise \(\PageIndex{31}\)

\(\frac{1}{\sqrt{250}}\)

Answer

\(\frac{1}{\sqrt{250}} = \frac{1}{\sqrt{2 \cdot 5^3}} = \frac{1}{\sqrt{2 \cdot 5^3}} \cdot \frac{\sqrt{2 \cdot 5}}{\sqrt{2 \cdot 5}} = \frac{\sqrt{2 \cdot 5}}{2^2 \cdot 5^4} = \frac{\sqrt{2 \cdot 5}}{2 \cdot 5^2} = \frac{\sqrt{10}}{50}\)

Exercise \(\PageIndex{32}\)

\(\frac{1}{\sqrt{108}}\)

Exercise \(\PageIndex{33}\)

\(\sqrt{\frac{5}{96}}\)

Answer

\(\sqrt{\frac{5}{96}} = \sqrt{\frac{5}{2^5 \cdot 3}} = \sqrt{\frac{5}{2^5 \cdot 3} \cdot \frac{2 \cdot 3}{2 \cdot 3}} = \sqrt{\frac{2 \cdot 3 \cdot 5}{2^6 \cdot 3^2}} = \frac{\sqrt{2 \cdot 3 \cdot 5}}{2^3 \cdot 3} = \frac{\sqrt{30}}{24}\)

Exercise \(\PageIndex{34}\)

\(\sqrt{\frac{2}{135}}\)

Exercise \(\PageIndex{35}\)

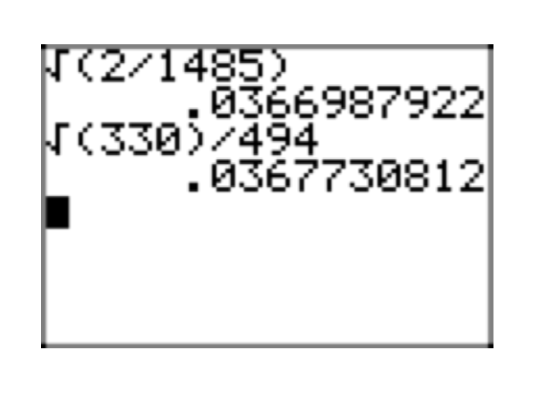
\(\sqrt{\frac{2}{1485}}\)

Answer

\(\sqrt{\frac{2}{1485}} = \sqrt{\frac{2}{3^3 \cdot 5 \cdot 11}} = \sqrt{\frac{2}{3^3 \cdot 5 \cdot 11} \cdot \frac{3 \cdot 5 \cdot 11}{3 \cdot 5 \cdot 11}} = \sqrt{\frac{2 \cdot 3 \cdot 5 \cdot 11}{3^4 \cdot 5^2 \cdot 11^2}} = \frac{\sqrt{2 \cdot 3 \cdot 5 \cdot 11}}{3^2 \cdot 5 \cdot 11} = \frac{\sqrt{330}}{494}\)

Exercise \(\PageIndex{36}\)

\(\sqrt{\frac{3}{280}}\)

In Exercises 37-44, place each of the given radical expressions in simple radical form. Make no assumptions about the sign of any variable. Variables can represent either positive or negative numbers.

Exercise \(\PageIndex{37}\)

\(\sqrt{\frac{8}{x^4}}\)

Answer

\(\sqrt{\frac{8}{x^4}} = \frac{\sqrt{8}}{\sqrt{x^4}} = \frac{\sqrt{4}\sqrt{2}}{|x^2|} = \frac{2\sqrt{2}}{x^2}\)

Exercise \(\PageIndex{38}\)

\(\sqrt{\frac{12}{x^6}}\)

Exercise \(\PageIndex{39}\)

\(\sqrt{\frac{20}{x^2}}\)

Answer

\(\sqrt{\frac{20}{x^2}} = \frac{\sqrt{20}}{\sqrt{x^2}} = \frac{\sqrt{4}\sqrt{5}}{|x|} = \frac{2\sqrt{5}}{|x|}\)

Exercise \(\PageIndex{40}\)

\(\sqrt{\frac{32}{x^{12}}}\)

Exercise \(\PageIndex{41}\)

\(\frac{2}{\sqrt{8x^8}}\)

Answer

\(\frac{2}{\sqrt{8x^8}} = \frac{2}{\sqrt{8x^8}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{2\sqrt{2}}{\sqrt{16x^8}} = \frac{2\sqrt{2}}{|4x^4|} = \frac{2\sqrt{2}}{4x^4}\)

Exercise \(\PageIndex{42}\)

\(\frac{3}{\sqrt{12x^6}}\)

Exercise \(\PageIndex{43}\)

\(\frac{10}{\sqrt{20x^{10}}}\)

Answer

\(\frac{10}{\sqrt{20x^{10}}} = \frac{10}{\sqrt{20x^{10}}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{10\sqrt{5}}{\sqrt{100x^{10}}} = \frac{10\sqrt{5}}{|10x^5|}\)

However, \(|10x^5| = |10||x^4||x| = 10x^{4}|x|\), so

\(\frac{10}{\sqrt{20x^{10}}} = \frac{10\sqrt{5}}{10x^{4}|x|} = \frac{\sqrt{5}}{x^{4}|x|}\).

Exercise \(\PageIndex{44}\)

\(\frac{12}{\sqrt{6x^4}}\)​​​

In Exercises 45-48, follow the lead of Example 8 in the narrative to craft a solution.

Exercise \(\PageIndex{45}\)

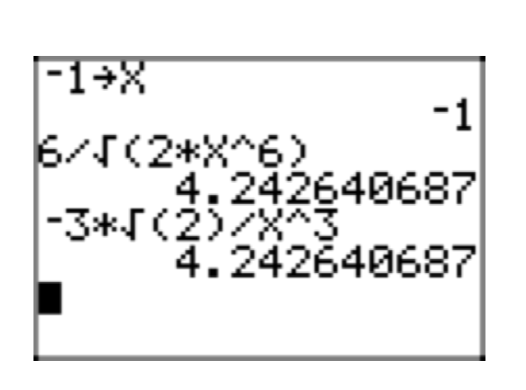
Given that x < 0, place the radical expression \(\frac{6}{\sqrt{2x^6}}\) in simple radical form. Check your solution on your calculator for x = −1.

Answer

\(\frac{6}{\sqrt{2x^6}} = \frac{6}{\sqrt{2x^6}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{6\sqrt{2}}{\sqrt{4x^6}} = \frac{6\sqrt{2}}{|2x^3|}\)

However, \(|2x^3| = |2||x^2||x| = 2x^{2}|x|\), so

\(\frac{6\sqrt{2}}{|2x^3|} = \frac{6\sqrt{2}}{2x^{2}|x|} = \frac{3\sqrt{2}}{x^{2}|x|}\).

If x < 0, then |x| = −x and

\(\frac{3\sqrt{2}}{x^{2}|x|} = \frac{3\sqrt{2}}{x^{2}(−x)} = −\frac{3\sqrt{2}}{x^3}\).

Checking x = −1.

Exercise \(\PageIndex{46}\)

Given that x > 0, place the radical expression \(\frac{4}{\sqrt{12x^3}}\) in simple radical form. Check your solution on your calculator for x = 1.

Exercise \(\PageIndex{47}\)

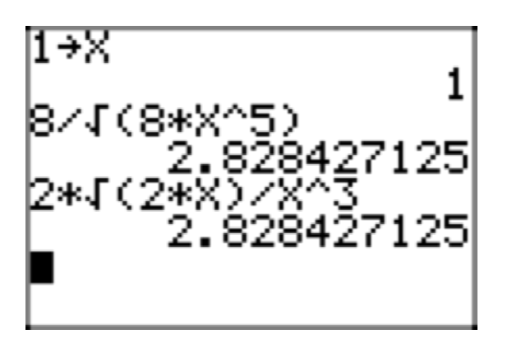
Given that x > 0, place the radical expression \(\frac{8}{\sqrt{8x^5}}\) in simple radical form. Check your solution on your calculator for x = 1.

Answer

\(\frac{8}{\sqrt{8x^5}} = \frac{8}{\sqrt{8x^5}} \cdot \frac{\sqrt{2x}}{\sqrt{2x}} = \frac{8\sqrt{2x}}{\sqrt{16x^6}} = \frac{8\sqrt{2x}}{|4x^3|}\)

However, \(|4x^3| = |4||x^2||x| = 4x^{2}|x|\), so

\(\frac{8\sqrt{2x}}{|4x^3|} = \frac{8\sqrt{2x}}{4x^{2}|x|} = \frac{2\sqrt{2x}}{x^{2}|x|}\).

But x > 0, so |x| = x and

\(\frac{2\sqrt{2x}}{x^{2}|x|} = \frac{2\sqrt{2x}}{x^{2}(x)} = \frac{2\sqrt{2x}}{x^3}\).

Checking x = 1.

Exercise \(\PageIndex{48}\)

Given that x < 0, place the radical expression \(\frac{15}{\sqrt{20x^6}}\) in simple radical form. Check your solution on your calculator for x = −1.

In Exercises 49-56, place each of the radical expressions in simple form. Assume that all variables represent positive numbers.

Exercise \(\PageIndex{49}\)

\(\sqrt{\frac{12}{x}}\)

Answer

\(\sqrt{\frac{12}{x}} = \sqrt{\frac{12}{x} \cdot \frac{x}{x}} = \sqrt{\frac{12x}{x^2}} = \frac{\sqrt{4}\sqrt{3x}}{\sqrt{x^2}} = \frac{2\sqrt{3x}}{x}\)

Exercise \(\PageIndex{50}\)

\(\sqrt{\frac{18}{x}}\)

Exercise \(\PageIndex{51}\)

\(\sqrt{\frac{50}{x^3}}\)

Answer

\(\sqrt{\frac{50}{x^3}} = \sqrt{\frac{50}{x^3} \cdot \frac{x}{x}} = \sqrt{\frac{50x}{x^4}} = \frac{\sqrt{25}\sqrt{2x}}{\sqrt{x^4}} = \frac{5\sqrt{2x}}{x^2}\)

Exercise \(\PageIndex{52}\)

\(\sqrt{\frac{72}{x^5}}\)

Exercise \(\PageIndex{53}\)

\(\frac{1}{\sqrt{50x}}\)

Answer

\(\frac{1}{\sqrt{50x}} = \frac{1}{\sqrt{50x}} \cdot \frac{\sqrt{2x}}{\sqrt{2x}} = \frac{\sqrt{2x}}{\sqrt{100x^2}} = \frac{\sqrt{2x}}{10x}\)

Exercise \(\PageIndex{54}\)

\(\frac{2}{\sqrt{18x}}\)

Exercise \(\PageIndex{55}\)

\(\frac{3}{\sqrt{27x^3}}\)

Answer

\(\frac{3}{\sqrt{27x^3}} = \frac{3}{\sqrt{27x^3}} \cdot \frac{\sqrt{3x}}{\sqrt{3x}} = \frac{3\sqrt{3x}}{\sqrt{81x^4}} = \frac{3\sqrt{3x}}{9x^2} = \frac{\sqrt{3x}}{3x^2}\)

Exercise \(\PageIndex{56}\)

\(\frac{5}{\sqrt{10x^5}}\)