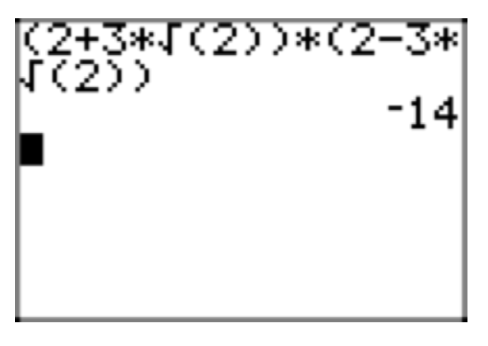9.4: Radical Expressions

In the previous two sections, we learned how to multiply and divide square roots. Specifically, we are now armed with the following two properties.

Property \(\PageIndex{1}\)

Let a and b be any two real nonnegative numbers. Then,

\[\sqrt{a}\sqrt{b} = \sqrt{ab}, \nonumber \]

and, provide \(b \ne 0\),

\[\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \nonumber \]

In this section, we will simplify a number of more extensive expressions containing square roots, particularly those that are fundamental to your work in future mathematics courses. Let’s begin by building some fundamental skills.

The Associative Property

We recall the associative property of multiplication.

Associative Property of Multiplication

Let a, b, and c be any real numbers. The associative property of multiplication states that

\[(ab)c = a(bc) \label{associativeprop} \]

Note that the order of the numbers on each side of Equation \ref{associativeprop} has not changed. The numbers on each side of the equation are in the order \(a\), \(b\), and then \(c\).

However, the grouping has changed. On the left, the parentheses around the product of \(a\) and \(b\) instruct us to perform that product first, then multiply the result by \(c\). On the right, the grouping is different; the parentheses around b and c instruct us to perform that product first, then multiply by \(a\). The key point to understand is the fact that the different groupings make no difference. We get the same answer in either case.

For example, consider the product \(2 \cdot 3 \cdot 4\). If we multiply 2 and 3 first, then multiply the result by 4, we get

\((2 \cdot 3) \cdot 4 = 6 \cdot 4 =24\)

On the other hand, if we multiply 3 and 4 first, then multiply the result by 2, we get

\(2 \cdot (3 \cdot 4) = 2 \cdot 12 =24\)

Note that we get the same result in either case. That is,

\((2 \cdot 3) \cdot 4 = 2 \cdot (3 \cdot 4)\)

The associative property, seemingly trivial, takes on an extra level of sophistication if we apply it to expressions containing radicals. Let’s look at an example.

Example \(\PageIndex{3}\)

Simplify the expression \(3(2\sqrt{5})\). Place your answer in simple radical form.

Currently, the parentheses around 2 and \(\sqrt{5}\) require that we multiply those two numbers first. However, the associative property of multiplication allows us to regroup, placing the parentheses around 3 and 2, multiplying those two numbers first, then multiplying the result by \(\sqrt{5}\). We arrange the work as follows.

\(3(2\sqrt{5})=(3 \cdot 2)\sqrt{5}=6\sqrt{5}\).

Readers should note the similarity to a very familiar manipulation.

\(3(2x) = (3 \cdot 2)x = 6x\)

In practice, when we became confident with this regrouping, we began to skip the intermediate step and simply state that 3(2x) = 6x. In a similar vein, once you become confident with regrouping, you should simply state that \(3(2\sqrt{5}) = 6\sqrt{5}\). If called upon to explain your answer, you must be ready to explain how you regrouped according to the associative property of multiplication. Similarly,

\(−4(5\sqrt{7})=−20\sqrt{7}\), \(12(5\sqrt{11})=60\sqrt{11}\), and \(−5(−3\sqrt{3})=15\sqrt{3}\).

The Commutative Property of Multiplication

We recall the commutative property of multiplication.

Commutative property of multiplication

Let a and b be any real numbers. The commutative property of multiplication states that

ab = ba

The commutative property states that the order of multiplication is irrelevant. For example, \(2 \cdot 3\) is the same as \(3 \cdot 2\); they both equal 6. This seemingly trivial property, coupled with the associative property of multiplication, allows us to change the order of multiplication and regroup as we please.

Example \(\PageIndex{5}\)

Simplify the expression \(\sqrt{5}(2\sqrt{3})\). Place your answer in simple radical form.

What we’d really like to do is first multiply \(\sqrt{5}\) and \(\sqrt{3}\). In order to do this, we must first regroup, then switch the order of multiplication as follows.

\(\sqrt{5}(2\sqrt{3}) = (\sqrt{5} \cdot 2)\sqrt{3} = (2\sqrt{5})\sqrt{3}\)

This is allowed by the associative and commutative properties of multiplication. Now, we regroup again and multiply.

\((2\sqrt{5})\sqrt{3} = 2(\sqrt{5}\sqrt{3}) = 2\sqrt{15}\)

In practice, this is far too much work for such a simple calculation. Once we understand the associative and commutative properties of multiplication, the expression \(a \cdot b \cdot c\) is unambiguous. Parentheses are not needed. We know that we can change the order of multiplication and regroup as we please. Therefore, when presented with the product of three numbers, simply multiply two of your choice together, then multiply the result by the third remaining number.

In the case of \(\sqrt{5}(2\sqrt{3})\), we choose to first multiply \(\sqrt{5}\) and \(\sqrt{3}\), which is \(\sqrt{15}\), then multiply this result by 2 to get \(2\sqrt{15}\). Similarly,

\(\sqrt{5}(2\sqrt{7})=2\sqrt{35}\) and \(\sqrt{x}(3\sqrt{5})=3\sqrt{5x}\).

Example \(\PageIndex{6}\)

Simplify the expression \(\sqrt{6}(4\sqrt{8})\). Place your answer in simple radical form.

We start by multiplying \(\sqrt{6}\) and \(\sqrt{8}\), then the result by 4.

\(\sqrt{6}(4\sqrt{8})=4\sqrt{48}\)

Now, \(48 = 16 \cdot 3\), so we can extract a perfect square.

\(4\sqrt{48}=4(\sqrt{16}\sqrt{3})=4(4\sqrt{3})\)

Again, we choose to multiply the fours, then the result by the square root of three. That is,

\(4(4\sqrt{3})=16\sqrt{3}\).

By induction, we can argue that the associative and commutative properties will allow us to group and arrange the product of more than three numbers in any order that we please.

Example \(\PageIndex{7}\)

Simplify the expression \(2\sqrt{12}(3\sqrt{3})\). Place your answer in simple radical form.

We’ll first take the product of 2 and 3, then the product of \(\sqrt{12}\) and \(\sqrt{3}\), then multiply these results together.

\(2\sqrt{12}(3\sqrt{3}) = (2 \cdot 3)(\sqrt{12}\sqrt{3}) = 6\sqrt{36}\)

Of course, \(\sqrt{36} = 6\), so we can simplify further.

\(6\sqrt{36} = 6 \cdot 6 = 36\)

The Distributive Property

Recall the distributive property for real numbers.

Distributive property

Let a, b, and c be any real numbers. Then,

a(b+c) = ab + ac

You might recall the following operation, where you “distribute the 2,” multiplying each term in the parentheses by 2.

​​​​2(3 + x) = 6 + 2x

You can do precisely the same thing with radical expressions.

\(2(3+\sqrt{5})=6+2\sqrt{5}\)

Like the familiar example above, we “distributed the 2,” multiplying each term in the parentheses by 2.

Let’s look at more examples.

Example \(\PageIndex{9}\)

Use the distributive property to expand the expression \(\sqrt{12}(3+\sqrt{3})\), placing your final answer in simple radical form.

First, distribute the \(\sqrt{12}\), multiplying each term in the parentheses by \(\sqrt{12}\). Note that \(\sqrt{12}\sqrt{3} = \sqrt{36}\).

\(\sqrt{12}(3+\sqrt{3})=3\sqrt{12}+\sqrt{36}=3\sqrt{12}+6\)

However, this last expression is not in simple radical form, as we can factor out a perfect square \((12 = 4 \cdot 3)\).

\(3\sqrt{12}+6=3(\sqrt{4}\sqrt{3})+6 = 3(2\sqrt{3})+6 = 6\sqrt{3}+6\)

It doesn’t matter whether the monomial factor is in the front or rear of the sum, you still distribute the monomial times each term in the parentheses.

Example \(\PageIndex{10}\)

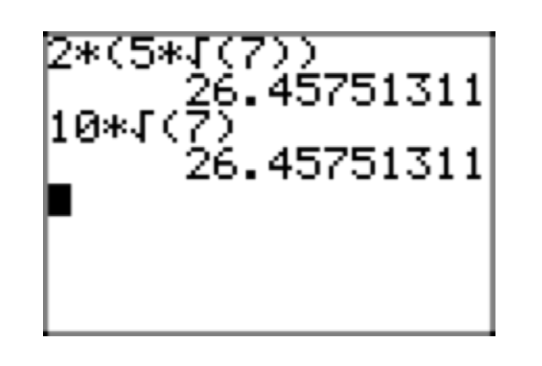
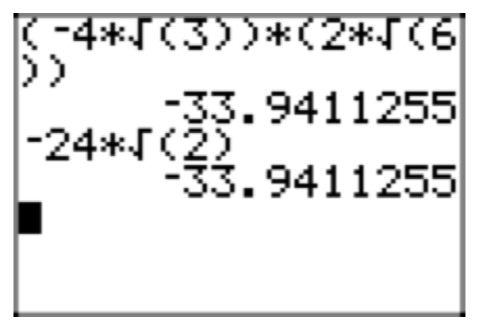
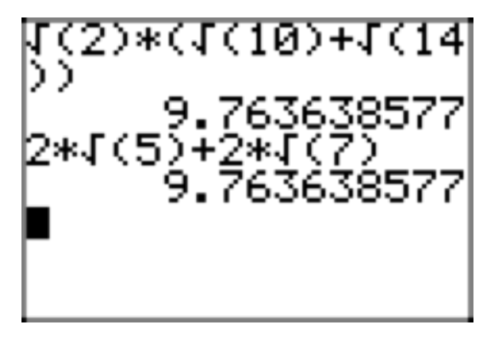
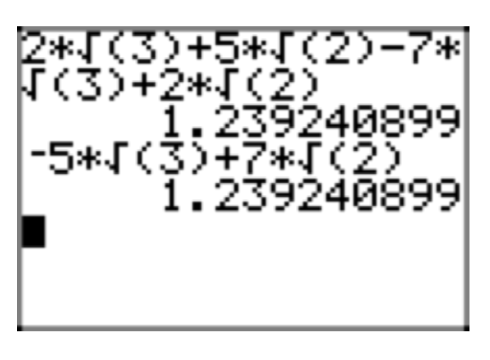
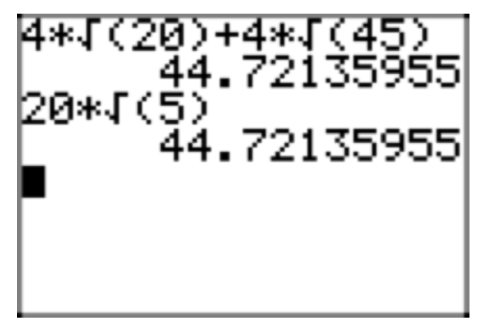
Use the distributive property to expand \((\sqrt{3}+2\sqrt{2})\sqrt{6}\). Place your answer in simple radical form.

First, multiply each term in the parentheses by \(\sqrt{6}\).

\((\sqrt{3}+2\sqrt{2})\sqrt{6} = \sqrt{18}+2\sqrt{12}\)

To obtain the second term of this result, we chose to first multiply \(\sqrt{2}\) and \(\sqrt{6}\), which is \(\sqrt{12}\), then we multiplied this result by 2. Now, we can factor perfect squares from both 18 and 12.

\(\sqrt{18}+2\sqrt{12}= \sqrt{9}\sqrt{2}+2(\sqrt{4}\sqrt{3}) = 3\sqrt{2}+2(2\sqrt{3}) = 3\sqrt{2}+4\sqrt{3}\)

Remember, you can check your results with your calculator. In Figure 1(a), we've found a decimal approximation for the original expression \((\sqrt{3}+2\sqrt{2})\sqrt{6}\), and in Figure 1(b) we have a decimal approximation for our solution \(3\sqrt{2}+4\sqrt{3}\). Note that they are the same, providing evidence that our solution is correct.

Figure 1. Comparing the original expression with its simple radical form.

The distributive property is also responsible in helping us combine “like terms.” For example, you might remember that 3x + 5x = 8x, a seemingly simple calculation, but it is the distributive property that actually provides this solution. Note how we use the distributive property to factor x from each term.

3x+5x = (3+5)x

Hence, 3x + 5x = 8x. You can do the same thing with radical expressions.

\(3\sqrt{2}+5\sqrt{2} = (3+5)\sqrt{2}\)

Hence, \(3\sqrt{2}+5\sqrt{2} = 8\sqrt{2}\) and the structure of this result is identical to that shown in 3x + 5x = 8x. There is no difference in the way we combine these “like terms.” We repeat the common factor and add coefficients. For example,

\(2\sqrt{3}+9\sqrt{3} = 11\sqrt{3}\), \(−4\sqrt{2}+2\sqrt{2} = −2\sqrt{2}\), and \(−3x\sqrt{x}+5x\sqrt{x}=2x\sqrt{x}\).

In each case above, we’re adding “like terms,” by repeating the common factor and adding coefficients.

In the case that we don’t have like terms, as in 3x+5y, there is nothing to be done. In like manner, each of the following expressions have no like terms that you can combine. They are as simplified as they are going to get.

\(3\sqrt{2}+5\sqrt{3}\), \(2\sqrt{11}−8\sqrt{10}\), and \(2\sqrt{x} + 5\sqrt{y}\)

However, there are times when it can look as if you don’t have like terms, but when you place everything in simple radical form, you discover that you do have like terms that can be combined by adding coefficients.

Example \(\PageIndex{11}\)

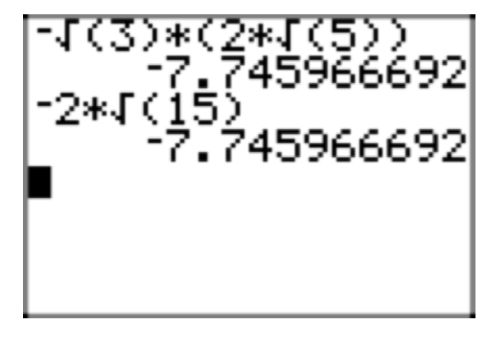
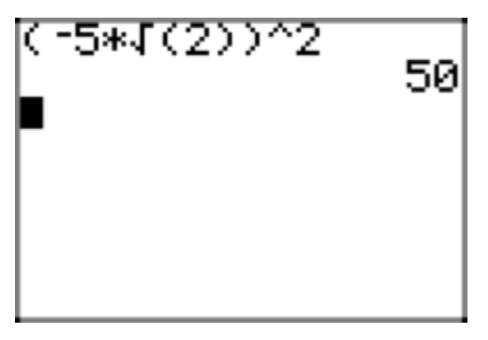
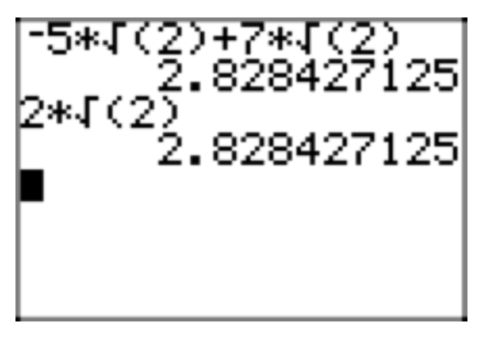
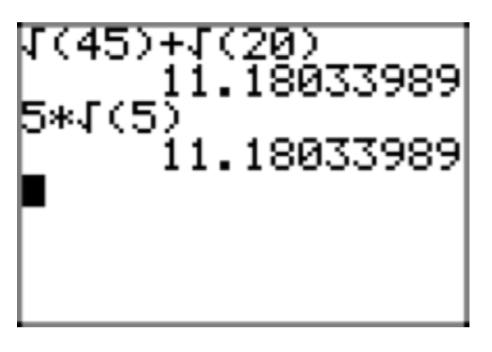
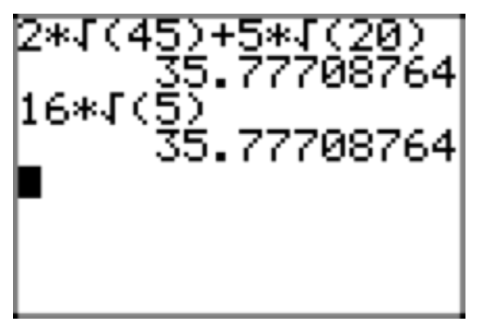
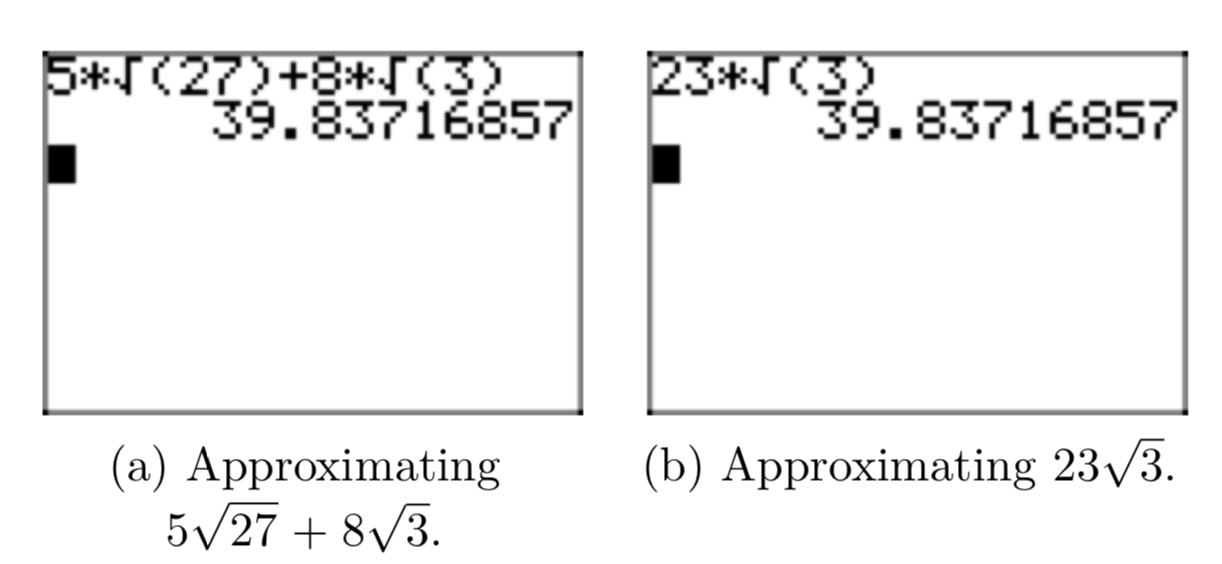
Simplify the expression \(5\sqrt{27}+8\sqrt{3}\), placing the final expression in simple radical form.

We can extract a perfect square (\(27 = 9 \cdot 3\)).

\(5\sqrt{27}+8\sqrt{3} = 5(\sqrt{9}\sqrt{3})+8\sqrt{3} = 5(3\sqrt{3})+8\sqrt{3} = 15\sqrt{3}+8\sqrt{3}\)

Note that we now have “like terms” that can be combined by adding coefficients.

\(15\sqrt{3}+8\sqrt{3} =23\sqrt{3}\)

A comparison of the original expression and its simplified form is shown in Figures 2(a) and (b).

Figure 2. Comparing the original expression with its simplified form.

Example \(\PageIndex{12}\)

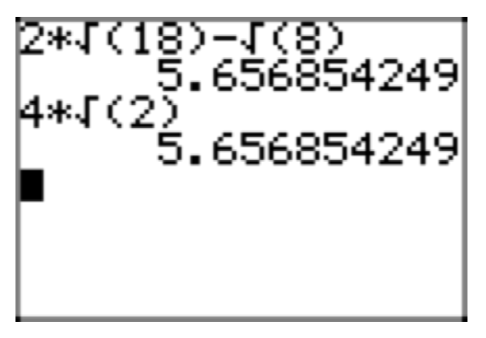
Simplify the expression \(2\sqrt{20}+\sqrt{8}+3\sqrt{5}+4\sqrt{2}\), placing the result in simple radical form.

We can extract perfect squares (\(20 = 4 \cdot 5\) and \(8 = 4 \cdot 2\)).

\(2\sqrt{20}+\sqrt{8}+3\sqrt{5}+4\sqrt{2} = 2(\sqrt{4}\sqrt{5})+\sqrt{4}\sqrt{2}+3\sqrt{5}+4\sqrt{2} = 2(2\sqrt{5})+2\sqrt{2}+3\sqrt{5}+4\sqrt{2} = 4\sqrt{5}+2\sqrt{2}+3\sqrt{5}+4\sqrt{2}\)

Now we can combine like terms by adding coefficients.

\(4\sqrt{5}+2\sqrt{2}+3\sqrt{5}+4\sqrt{2} = 7\sqrt{5}+6\sqrt{2}\)

Fractions can be a little tricky.

Example \(\PageIndex{13}\)

Simplify \(\sqrt{27}+\frac{1}{\sqrt{12}}\), placing the result in simple radical form.

We can extract a perfect square root \((27 = 9 \cdot 3)\) The denominator in the second term is \(\sqrt{12} = 2\sqrt{2} \cdot \sqrt{3}\), so one more 3 is needed in the denominator to make a perfect square.

\(\sqrt{27}+\frac{1}{\sqrt{12}} = \sqrt{9}\sqrt{3}+\frac{1}{\sqrt{12}} \cdot \frac{\sqrt{3}}{\sqrt{3}} = 3\sqrt{3}+\frac{\sqrt{3}}{\sqrt{36}} = 3\sqrt{3} + \frac{\sqrt{3}}{6}\)

To add these fractions, we need a common denominator of 6.

\(3\sqrt{3} + \frac{\sqrt{3}}{6} = \frac{18\sqrt{3}}{6} + \frac{\sqrt{3}}{6} = \frac{19\sqrt{3}}{6}\)

We can now combine numerators by adding coefficients.

\(\frac{18\sqrt{3}}{6} + \frac{\sqrt{3}}{6} = \frac{19\sqrt{3}}{6}\)

Decimal approximations of the original expression and its simplified form are shown in Figures 3(a) and (b).

Figure 3. Comparing the original expression with its simplified form.

At first glance, the lack of a monomial in the product (x + 1)(x + 3) makes one think that the distributive property will not help us find the product. However, if we think of the second factor as a single unit, we can distribute it times each term in the first factor.

(x+1)(x+3) = x(x+3)+1(x+3)

Apply the distributive property a second time, then combine like terms.

\(x(x+3)+1(x+3)=x^2+3x+x+3 = x^2+4x+3\)

We can handle products with radical expressions in the same manner.

Example \(\PageIndex{14}\)

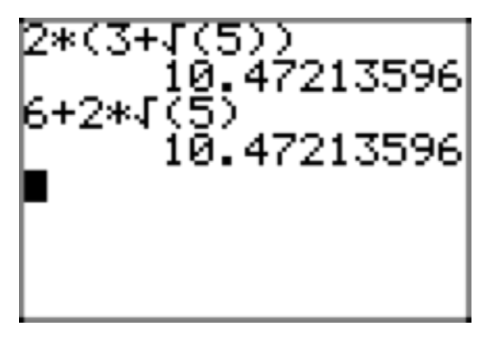
Simplify \((2+\sqrt{2})(3+5\sqrt{2})\). Place your result in simple radical form.

Think of the second factor as a single unit and distribute it times each term in the first factor.

\((2+\sqrt{2})(3+5\sqrt{2}) = 2(3+5\sqrt{2})+\sqrt{2}(3+5\sqrt{2})\)

Now, use the distributive property again.

\(2(3+5\sqrt{2})+\sqrt{2}(3+5\sqrt{2}) = 6+10\sqrt{2}+3\sqrt{2}+5\sqrt{4}\)

Note that in finding the last term, \(\sqrt{2}\sqrt{2} = \sqrt{4}\). Now, \sqrt{4} = 2, then we can combine like terms.

\(6+10\sqrt{2}+3\sqrt{2}+5\sqrt{4} = 6+10\sqrt{2}+3\sqrt{2}+5(2) = 6+10\sqrt{2}+3\sqrt{2}+10 = 16+13\sqrt{2}\)

Decimal approximations of the original expression and its simple radical form are shown in Figures 4(a) and (b).

Figure 4. Comparing the original expression with its simplified form.

Special Products

There are two special products that have important applications involving radical expressions, perhaps one more than the other. The first is the well-known difference of two squares pattern.

Difference of squares

Let a and b be any numbers. Then,

\((a+b)(a−b)=a^2−b^2\).

This pattern involves two binomial factors having identical first and second terms, the terms in one factor separated by a plus sign, the terms in the other factor separated by a minus sign. When we see this pattern of multiplication, we should square the first term of either factor, square the second term, then subtract the results. For example,

\((2x+3)(2x−3) = 4x^2−9\).

This special product applies equally well when the first and/or second terms involve radical expressions.

Example \(\PageIndex{15}\)

Use the difference of squares patterns to multiply \((2+\sqrt{11})(2−\sqrt{11})\)

Note that this multiplication has the form (a + b)(a − b), so we apply the difference of squares pattern to get

\((2+\sqrt{11})(2−\sqrt{11}) = (2)^2−(\sqrt{11})^2\)

Of course, \(2^2 = 4\) and \((\sqrt{11})^2 = 11\), so we can finish as follows.

\((2)^2−(\sqrt{11})^2 = 4−11 = −7\)

Example \(\PageIndex{16}\)

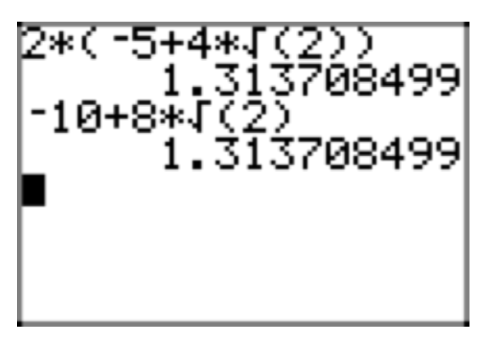
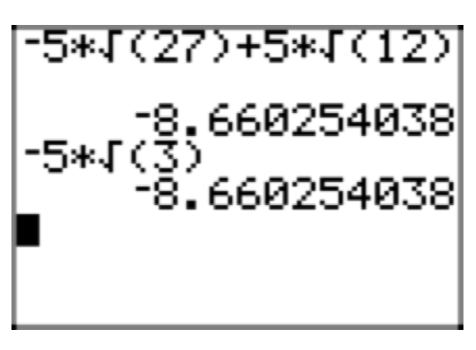
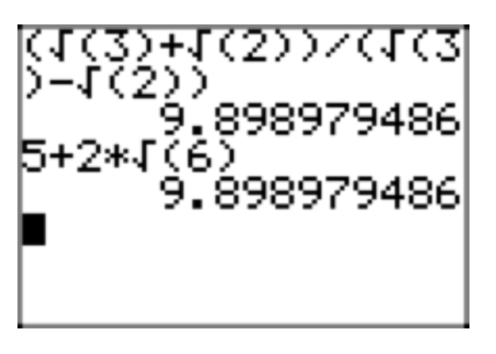
Use the difference of squares pattern to multiply \((2\sqrt{5}+3\sqrt{7})(2\sqrt{5}−3\sqrt{7})\).

Again, this product has the special form (a + b)(a − b), so we apply the difference of squares pattern to get

\((2\sqrt{5}+3\sqrt{7})(2\sqrt{5}−3\sqrt{7}) = (2\sqrt{5})^2−(3\sqrt{7})^2\)

Next, we square a product of two factors according to the rule \((ab)^2 = a^{2}b^2\). Thus,

\((2\sqrt{5})^2 = (2)^{2}(\sqrt{5})^2 = 4 \cdot 5 = 20\)

and

\((3\sqrt{7})^2 =(3)^{2}(\sqrt{7})^2 = 9 \cdot 7 = 63\).

Thus, we can complete the multiplication \((2\sqrt{5}+3\sqrt{7})(2\sqrt{5}−3\sqrt{7})\) with

\((2\sqrt{5})^2−(3\sqrt{7})^2 =20−63=−43\).

This result is easily verified with a calculator, as shown in Figure 5.

Figure 5. Approximating \((2\sqrt{5}+3\sqrt{7})(2\sqrt{5}−3\sqrt{7})\).

The second pattern of interest is the shortcut for squaring a binomial.

Squaring a binomial

Let a and b be numbers. Then,

\((a + b)^2 = a^2 + 2ab + b^2\).

Here we square the first and second terms of the binomial, then produce the middle term of the result by multiplying the first and second terms and doubling that result. For example,

\((2x+9)^2 = (2x)^2 +2(2x)(9)+(9)^2 = 4x^2 +36x+81\).

This pattern can also be applied to binomials containing radical expressions.

Example \(\PageIndex{17}\)

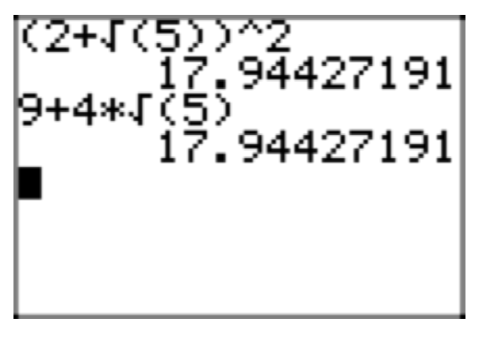
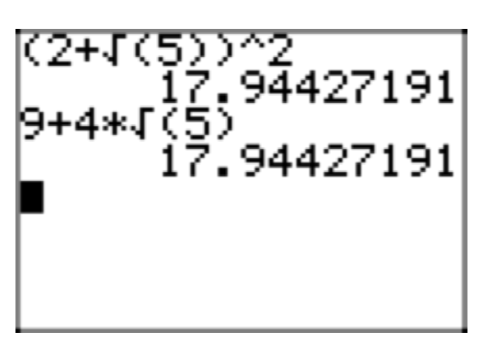
Use the squaring a binomial pattern to expand \((2\sqrt{x} + \sqrt{5})^2\). Place your result in simple radical form. Assume that x is a positive real number (x > 0).

Applying the squaring a binomial pattern, we get

\((2\sqrt{x} + \sqrt{5})^2 = (2\sqrt{x})^2 + 2(2\sqrt{x})(\sqrt{5}) + (\sqrt{5})^2\).

As before, \((2\sqrt{x})^2 = (2)^{2}(\sqrt{x})^2 = 4x\) and \((\sqrt{5})^2 = 5\). In the case of \(2(2\sqrt{x})(\sqrt{5})\), note that we are multiplying four numbers together. The associative and commutative properties state that we can multiply these four numbers in any order that we please. So, the product of 2 and 2 is 4, the product of \(\sqrt{x}\) and \(\sqrt{5}\) is \(\sqrt{5x}\), then we multiply these results to produce the result \(4\sqrt{5x}\). Thus,

\((2\sqrt{x})^2 + 2(2\sqrt{x})(\sqrt{5}) + (\sqrt{5})^2 = 4x + 4\sqrt{5x} + 5\).

Rationalizing Denominators

As we saw in the previous section, the instruction “rationalize the denominator” is a request to remove all radical expressions from the denominator. Of course, this is the “third guideline of simple radical form,” but there are times, particularly in calculus, when the instruction changes to “rationalize the numerator.” Of course, this is a request to remove all radicals from the numerator.

You can’t have both worlds. You can either remove radical expressions from the denominator or from the numerator, but not both. If no instruction is given, assume that the “third guideline of simple radical form” is in play and remove all radical expressions from the denominator. We’ve already done a little of this in previous sections, but here we address a slightly more complicated type of expression.

Example \(\PageIndex{18}\)

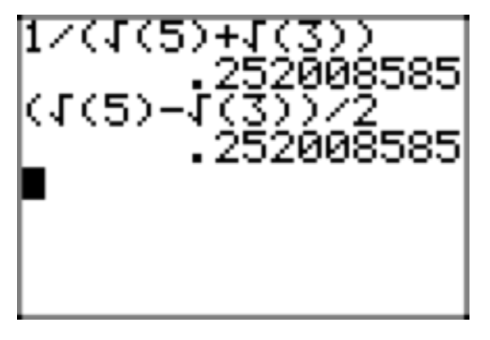
In the expression \(\frac{3}{2+\sqrt{2}}\), rationalize the denominator.

The secret lies in the difference of squares pattern, \((a+b)(a−b) = a^2−b^2\). For example,

\((2+\sqrt{2})(2−\sqrt{2}) = (2)^2−(\sqrt{2})^2 = 4−2 = 2\).

This provides a terrific hint at how to proceed with rationalizing the denominator of the expression \(\frac{3}{(2+\sqrt{2})}\). Multiply both numerator and denominator by \(2−\sqrt{2}\).

\(\frac{3}{2+\sqrt{2}} = \frac{3}{2+2\sqrt{2}} \cdot \frac{2−\sqrt{2}}{2−\sqrt{2}}\)

Multiply numerators and denominators.

\(\frac{3}{2+2\sqrt{2}} \cdot \frac{2−\sqrt{2}}{2−\sqrt{2}} = \frac{3(2−\sqrt{2})}{(2+\sqrt{2})(2−\sqrt{2})} = \frac{6−3\sqrt{2}}{(2)^2−(\sqrt{2})^2} = \frac{6−3\sqrt{2}}{4−2} = \frac{6−3\sqrt{2}}{2}\)

Note that it is tempting to cancel the 2 in the denominator into the 6 in the numerator, but you are not allowed to cancel terms that are separated by a minus sign. This is a common error, so don’t fall prey to this mistake.

In Figures 6(a) and (b), we compare decimal approximations of the original expression and its simple radical form.

Figure 6. Comparing the original expression with its simple radical form.

Example \(\PageIndex{19}\)

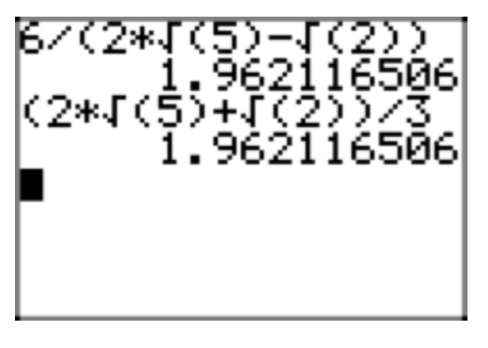
In the expression \(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}}\), rationalize the denominator.

Multiply numerator and denominator by \(\sqrt{3} + \sqrt{2}\).

\(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}} = \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}} \cdot \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}\).

Multiply numerators and denominators.

\(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}} \cdot \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}} = \frac{(\sqrt{3}+\sqrt{2})^2}{(\sqrt{3}−\sqrt{2})(\sqrt{3}+\sqrt{2})}\)

In the denominator, we have the difference of two squares. Thus,

\((\sqrt{3}−\sqrt{2})(\sqrt{3}+\sqrt{2}) = (\sqrt{3})^2−(\sqrt{2})^2 =3−2=1\).

Note that this clears the denominator of radicals. This is the reason we multiply numerator and denominator by \(\sqrt{3} + \sqrt{2}\). In the numerator, we can use the squaring a binomial shortcut to multiply.

\((\sqrt{3} + \sqrt{2})^2 = (\sqrt{3})^2 + 2(\sqrt{3})(\sqrt{2}) + (\sqrt{2})^2 = 3+2\sqrt{6} +2 = 5+2\sqrt{6}\)

Thus, we can complete the simplification started above.

\(\frac{(\sqrt{3}+\sqrt{2})^2}{(\sqrt{3}−\sqrt{2})(\sqrt{3}+\sqrt{2})} = \frac{5+2\sqrt{6}}{1} = 5+2\sqrt{6}\)

In Figures 7(a) and (b), we compare the decimal approximations of the original expression with its simple radical form.

Figure 7. Comparing the original expression with its simple radical form.

Revisiting the Quadratic Formula

We can use what we’ve learned to place solutions provided by the quadratic formula in simple form. Let’s look at an example.

Example \(\PageIndex{20}\)

Solve the equation \(x^2 = 2x + 2\) for x. Place your solution in simple radical form.

The equation is nonlinear, so make one side zero.

\(x^2−2x−2=0\)

Compare this result with the general form \(ax^2 +bx+c = 0\) and note that a = 1, b = −2 and c = −2. Write down the quadratic formula, make the substitutions, then simplify.

\(x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−2) \pm \sqrt{(−2)^2−4(1)(−2)}}{2(1)} = \frac{2 \pm \sqrt{12}}{2}\)

Note that we can factor a perfect square from the radical in the numerator.

\(x= \frac{2 \pm \sqrt{12}}{2} = \frac{2 \pm \sqrt{4}\sqrt{3}}{2} = \frac{2 \pm 2\sqrt{3}}{2}\)

At this point, note that both numerator and denominator are divisible by 2. There are several ways that we can proceed with the reduction.

• Some people prefer to factor, then cancel.

\(\frac{2 \pm 2\sqrt{3}}{2} = \frac{2(1 \pm \sqrt{3})}{2} = 1 \pm \sqrt{3}\)

• Some prefer to use the distributive property.

\(\frac{2 \pm 2\sqrt{3}}{2} = \frac{2}{2} \pm \frac{2\sqrt{3}}{2} = 1 \pm \sqrt{3}\)

In each case, the final form of the answer is in simple radical form and it is reduced to lowest terms.

Warning \(\PageIndex{21}\)

When working with the quadratic formula, one of the most common algebra mistakes is to cancel addends instead of factors, as in

\(\frac{2 \pm 2\sqrt{3}}{2} = \pm 2\sqrt{3}\)

Please try to avoid making this mistake.

Let’s look at another example.

Example \(\PageIndex{22}\)

Solve the equation \(3x^2 − 2x = 6\) for x. Place your solution in simple radical form.

This equation is nonlinear. Move every term to one side of the equation, making the other side of the equation equal to zero.

\(3x^2−2x−6=0\)

Compare with the general form \(ax^2 +bx+c = 0\) and note that a = 3, b = −2, and c = −6. Write down the quadratic formula and substitute.

\(x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−2) \pm \sqrt{(−2)^2−4(3)(−6)}}{2(3)} = \frac{2 \pm \sqrt{76}}{6}\)

Factor a perfect square from the radical in the numerator.

\(x = \frac{2 \pm \sqrt{76}}{6} = \frac{2 \pm \sqrt{4}\sqrt{19}}{6} = \frac{2 \pm 2\sqrt{19}}{6}\)

We choose to factor and cancel.

\(x = \frac{2 \pm 2\sqrt{19}}{6} = \frac{2(1 \pm \sqrt{19})}{2 \cdot 3} = \frac{1 \pm \sqrt{19}}{3}\)

In Exercises 1-14, place each of the radical expressions in simple radical form. Check your answer with your calculator.

Exercise \(\PageIndex{1}\)

\(2(5\sqrt{7})\)

Answer

Regroup using the associative property and simplify.

\(2(5\sqrt{7})=(2 \cdot 5)\sqrt{7}=10\sqrt{7}\)

Check.

Exercise \(\PageIndex{2}\)

\(−3(2\sqrt{3})\)

Exercise \(\PageIndex{3}\)

\(−\sqrt{3}(2\sqrt{5})\)

Answer

The commutative and associative properties allow us to reorder and regroup.

\(−\sqrt{3}(2\sqrt{5})=2(−\sqrt{3}\sqrt{5})=2(−\sqrt{15})=−2\sqrt{15}\)

Check.

Exercise \(\PageIndex{4}\)

\(\sqrt{2}(3\sqrt{7})\)

Exercise \(\PageIndex{5}\)

\(\sqrt{3}(5\sqrt{6})\)

Answer

The commutative and associative properties allow us to reorder and regroup.

\(\sqrt{3}(5\sqrt{6})=5(\sqrt{3}\sqrt{6})=5(\sqrt{18})\)

This is not in simple form as it is possible to factor out a perfect square.

\(5\sqrt{18}=5\sqrt{9}\sqrt{2}=5 \cdot 3\sqrt{2}=15\sqrt{2}\)

Check.

Exercise \(\PageIndex{6}\)

\(\sqrt{2}(−3\sqrt{10})\)

Exercise \(\PageIndex{7}\)

\((2\sqrt{5})(−3\sqrt{3})\)

Answer

The commutative and associative properties allow us to reorder and regroup.

\((2\sqrt{5})(−3\sqrt{3})=(2 \cdot −3)(\sqrt{5}\sqrt{3})=−6\sqrt{15}\)

Check.

Exercise \(\PageIndex{8}\)

\((−5\sqrt{2})(−2\sqrt{7})\)

Exercise \(\PageIndex{9}\)

\((−4\sqrt{3})(2\sqrt{6})\)

Answer

The commutative and associative properties allows us to reorder and regroup.

\((−4\sqrt{3})(2\sqrt{6}) = (−4 \cdot 2)(\sqrt{3}\sqrt{6})=−8\sqrt{18}\)

This answer is not in simple for because we can factor out a perfect square.

\(−8\sqrt{18} = −8\sqrt{9}\sqrt{2} = −8 \cdot 3\sqrt{2} = −24\sqrt{2}\)

Check.

Exercise \(\PageIndex{10}\)

\((2\sqrt{5})(−3\sqrt{10})\)

Exercise \(\PageIndex{11}\)

\((2\sqrt{3})^2\)

Answer

Recall that \((ab)^2 = a^{2}b^2\).

\((2\sqrt{3})^2 = (2)^{2}(\sqrt{3})^2 = 4 \cdot 3 = 12\)

Check.

Exercise \(\PageIndex{12}\)

\((−3\sqrt{5})^2\)

Exercise \(\PageIndex{13}\)

\((−5\sqrt{2})^2\)

Answer

Recall that \((ab)^2 = a^{2}b^2\).

\((−5\sqrt{2})^2 = (−5)^{2}(\sqrt{2})^2 = 25 \cdot 2 = 50\)

Check.

Exercise \(\PageIndex{14}\)

\((7\sqrt{11})^2\)

In Exercises 15-22, use the distributive property to multiply. Place your final answer in simple radical form. Check your result with your calculator.

Exercise \(\PageIndex{15}\)

\(2(3 +\sqrt{5})\)

Answer

Recall the distributive property: a(b + c) = ab + ac.

\(2(3+\sqrt{5}) = 2(3)+2(\sqrt{5}) = 6+2\sqrt{5}\)

Check.

Exercise \(\PageIndex{16}\)

\(−3(4−\sqrt{7})\)

Exercise \(\PageIndex{17}\)

\(2(−5+4\sqrt{2})\)

Answer

Recall the distributive property: a(b + c) = ab + ac.

\(2(−5+4\sqrt{2})=2(−5)+2(4\sqrt{2})=−10+8\sqrt{2}\)

Check.

Exercise \(\PageIndex{18}\)

\(−3(4−3\sqrt{2})\)

Exercise \(\PageIndex{19}\)

\(\sqrt{2}(2+\sqrt{2})\)

Answer

Recall the distributive property: a(b + c) = ab + ac.

\(\sqrt{2}(2+\sqrt{2}) = \sqrt{2}(2)+\sqrt{2}(\sqrt{2}) = 2\sqrt{2}+\sqrt{4}=2\sqrt{2}+2\)

Check.

Exercise \(\PageIndex{20}\)

\(\sqrt{3}(4−\sqrt{6})\)

Exercise \(\PageIndex{21}\)

\(\sqrt{2}(\sqrt{10}+\sqrt{14})\)

Answer

Recall the distributive property: a(b + c) = ab + ac.

\(\sqrt{2}(\sqrt{10}+\sqrt{14}) = \sqrt{2}(\sqrt{10})+ \sqrt{2}(\sqrt{14}) = \sqrt{20}+\sqrt{28}\)

However, this answer is not in simple form because we can factor out perfect squares.

\(\sqrt{20}+\sqrt{28} = \sqrt{4}\sqrt{5}+\sqrt{4}\sqrt{7} = 2\sqrt{5}+2\sqrt{7}\)

Check.

Exercise \(\PageIndex{22}\)

\(\sqrt{3}(\sqrt{15}−\sqrt{33})\)

In Exercises 23-30, combine like terms. Place your final answer in simple radical form. Check your solution with your calculator.

Exercise \(\PageIndex{23}\)

\(−5\sqrt{2}+7\sqrt{2}\)

Answer

Use the distributive property to factor out \(\sqrt{2}\).

\(−5\sqrt{2}+7\sqrt{2} = (−5+7)\sqrt{2} = 2\sqrt{2}\)

In practice, we usually just combine \(−5\sqrt{2}+7\sqrt{2}\) much as we do −5x+7x = 2x and simply write \(−5\sqrt{2}+7\sqrt{2}=2\sqrt{2}\).

Check.

Exercise \(\PageIndex{24}\)

\(2\sqrt{3}+3\sqrt{3}\)

Exercise \(\PageIndex{25}\)

\(2\sqrt{6}−8\sqrt{6}\)

Answer

Use the distributive property to factor out \(\sqrt{6}\).

\(2\sqrt{6}−8\sqrt{6} = (2−8)\sqrt{6} = −6\sqrt{6}\)

In practice, we usually just combine \(2\sqrt{6}−8\sqrt{6}\) much as we do 2x−8x = −6x and simply write \(2\sqrt{6}−8\sqrt{6}=−6\sqrt{6}\).

Check.

Exercise \(\PageIndex{26}\)

\(\sqrt{7}−3\sqrt{7}\)

Exercise \(\PageIndex{27}\)

\(2\sqrt{3}−4\sqrt{2}+3\sqrt{3}\)

Answer

The commutative and associative properties of addition allows us to reorder and regroup, then we combine like terms.

\(2\sqrt{3}−4\sqrt{2}+3\sqrt{3} = (2\sqrt{3}+3\sqrt{3})−4\sqrt{2} = 5\sqrt{3}−4\sqrt{2}\)

Check.

Exercise \(\PageIndex{28}\)

\(7\sqrt{5}+2\sqrt{7}−3\sqrt{5}\)

Exercise \(\PageIndex{29}\)

\(2\sqrt{3}+5\sqrt{2}−7\sqrt{3}+2\sqrt{2}\)

Answer

The commutative and associative properties of addition allow us to reorder and regroup, then we can add like terms.

\(2\sqrt{3}+5\sqrt{2}−7\sqrt{3}+2\sqrt{2} = (2\sqrt{3}−7\sqrt{3})+(5\sqrt{2}+2\sqrt{2})=−5\sqrt{3}+7\sqrt{2}\)

Check.

Exercise \(\PageIndex{30}\)

\(3\sqrt{11}−2\sqrt{7}−2\sqrt{11}+4\sqrt{7}\)

In Exercises 31-40, combine like terms where possible. Place your final answer in simple radical form. Use your calculator to check your result.

Exercise \(\PageIndex{31}\)

\(\sqrt{45}+\sqrt{20}\)

Answer

\(\sqrt{45}+\sqrt{20} = \sqrt{3^{2} \cdot 5}+ \sqrt{2^2 \cdot 5} = 3\sqrt{5}+2\sqrt{5} = (3+2)\sqrt{5} =5\sqrt{5}\)

Check.

Exercise \(\PageIndex{32}\)

\(−4\sqrt{45}−4\sqrt{20}\)

Exercise \(\PageIndex{33}\)

\(2\sqrt{18} − \sqrt{8}\)

Answer

\(2\sqrt{18}−\sqrt{8} = 2\sqrt{3^2 \cdot 2}−\sqrt{2^2 \cdot 2} = 6\sqrt{2}−2\sqrt{2} = (6−2)\sqrt{2} = 4\sqrt{2}\)

Check.

Exercise \(\PageIndex{34}\)

\(−\sqrt{20}+4\sqrt{45}\)

Exercise \(\PageIndex{35}\)

\(−5\sqrt{27}+5\sqrt{12}\)

Answer

\(−5\sqrt{27}+5\sqrt{12} = −5\sqrt{3^2 \cdot 3}+5\sqrt{2^2 \cdot 3} = −15\sqrt{3}+10\sqrt{3} = (−15+10)\sqrt{3} = −5\sqrt{3}\)

Check.

Exercise \(\PageIndex{36}\)

\(3\sqrt{12}−2\sqrt{27}\)

Exercise \(\PageIndex{37}\)

\(4\sqrt{20}+4\sqrt{45}\)

Answer

\(4\sqrt{20}+4\sqrt{45} = 4\sqrt{2^2 \cdot 5}+4\sqrt{3^2 \cdot 5} = 8\sqrt{5}+12\sqrt{5} = (8+12)\sqrt{5} =20\sqrt{5}\)

Check.

Exercise \(\PageIndex{38}\)

\(−2\sqrt{18}−5\sqrt{8}\)

Exercise \(\PageIndex{39}\)

\(2\sqrt{45}+5\sqrt{20}\)

Answer

\(2\sqrt{45}+5\sqrt{20} = 2\sqrt{3^2 \cdot 5}+5\sqrt{2^2 \cdot 5} = 6\sqrt{5}+10\sqrt{5} = 16\sqrt{5}\)

Check.

Exercise \(\PageIndex{40}\)

\(3\sqrt{27}−4\sqrt{12}\)

In Exercises 41-48, simplify each of the given rational expressions. Place your final answer in simple radical form. Check your result with your calculator.

Exercise \(\PageIndex{41}\)

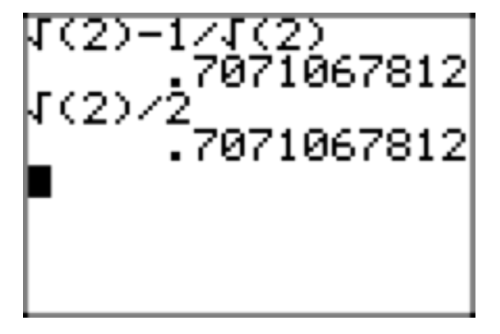
\(\sqrt{2}−\frac{1}{\sqrt{2}}\)

Answer

Place the second term in simple radical form.

\(\sqrt{2}−\frac{1}{\sqrt{2}} = \sqrt{2}−\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \sqrt{2}−\frac{\sqrt{2}}{\sqrt{4}} = \sqrt{2}−\frac{\sqrt{2}}{2}\)

Write each term over a common denominator of 2.

\(\sqrt{2}−\frac{\sqrt{2}}{2} = \sqrt{2} \cdot \frac{2}{2}−\frac{\sqrt{2}}{2} = \frac{2\sqrt{2}}{2}−\frac{\sqrt{2}}{2} = \frac{\sqrt{2}}{2}\)

Check.

Exercise \(\PageIndex{42}\)

\(3\sqrt{3}−\frac{3}{\sqrt{3}}\)

Exercise \(\PageIndex{43}\)

\(2\sqrt{2}−\frac{2}{\sqrt{2}}\)

Answer

Place the second term in simple radical form.

\(2\sqrt{2}−\frac{2}{\sqrt{2}} = 2\sqrt{2}−\frac{2}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = 2\sqrt{2}−\frac{2\sqrt{2}}{\sqrt{4}}\)

Continuing,

\(2\sqrt{2}−\frac{2\sqrt{2}}{\sqrt{4}} = 2\sqrt{2}−\frac{2\sqrt{2}}{2} = 2\sqrt{2}−\sqrt{2} = \sqrt{2}\)

Check.

Exercise \(\PageIndex{44}\)

\(4\sqrt{5}−\frac{5}{\sqrt{5}}\)

Exercise \(\PageIndex{45}\)

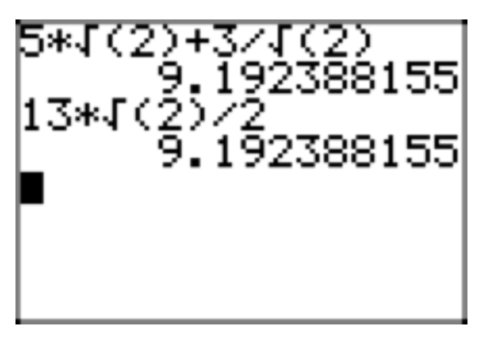
\(5\sqrt{2}+\frac{3}{\sqrt{2}}\)

Answer

Place the second term in simple radical form.

\(5\sqrt{2}+\frac{3}{\sqrt{2}} = 5\sqrt{2}+\frac{3}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = 5\sqrt{2}+\frac{3\sqrt{2}}{\sqrt{4}} = 5\sqrt{2}+\frac{3\sqrt{2}}{2}\)

Write equivalent fractions with a common denominator and add.

\(\sqrt{2}+\frac{3\sqrt{2}}{2} = 5\sqrt{2} \cdot \frac{2}{2}+\frac{3\sqrt{2}}{2} = \frac{10\sqrt{2}}{2}+\frac{3\sqrt{2}}{2} = \frac{13\sqrt{2}}{2}\)

Check.

Exercise \(\PageIndex{46}\)

\(6\sqrt{3}+\frac{2}{\sqrt{3}}\)

Exercise \(\PageIndex{47}\)

\(\sqrt{8}−\frac{12}{\sqrt{2}}−3\sqrt{2}\)

Answer

Place the first and second terms in simple radical form.

\(\sqrt{8}−\frac{12}{\sqrt{2}}−3\sqrt{2} = \sqrt{4}\sqrt{2}−\frac{12}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}}−3\sqrt{2} = 2\sqrt{2}−\frac{12\sqrt{2}}{2}−3\sqrt{2}\)

Reduce the fractional second term, then combine like terms.

\(2\sqrt{2}−\frac{12\sqrt{2}}{2}−3\sqrt{2} = 2\sqrt{2}−6\sqrt{2}−3\sqrt{2} = −7\sqrt{2}\)

Check.

Exercise \(\PageIndex{48}\)

\(\sqrt{27}−\frac{6}{\sqrt{3}}−5\sqrt{3}\)

In Exercises 49-60, multiply to expand each of the given radical expressions. Place your final answer in simple radical form. Use your calculator to check your result.

Exercise \(\PageIndex{49}\)

\((2+\sqrt{3})(3−\sqrt{3})\)

Answer

Distribute the second factor times each term of the first factor, then apply the distributive property a second time.

\((2+\sqrt{3})(3−\sqrt{3})=2(3−\sqrt{3})+\sqrt{3}(3−\sqrt{3})=6−2\sqrt{3}+3\sqrt{3}−\sqrt{9}\)

Simplify and combine like terms.

\(6−2\sqrt{3}+3\sqrt{3}−\sqrt{9}=6−2\sqrt{3}+3\sqrt{3}−3=3+\sqrt{3}\)

Check.

Exercise \(\PageIndex{50}\)

\((5+\sqrt{2})(2−\sqrt{2})\)

Exercise \(\PageIndex{51}\)

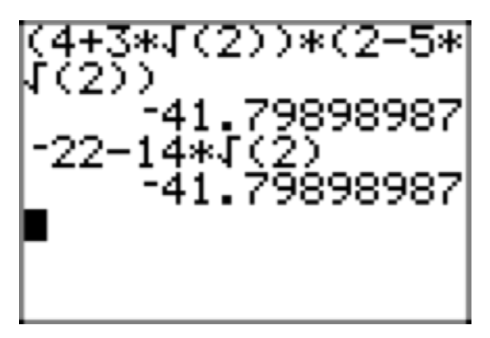
\((4+3\sqrt{2})(2−5\sqrt{2})\)

Answer

Use the distributive property to multiply the second factor times each term of the first factor, then use the distributive property a second time.

\((4+3\sqrt{2})(2−5\sqrt{2}) = 4(2−5\sqrt{2})+3\sqrt{2}(2−5\sqrt{2}) = 8−20\sqrt{2}+6\sqrt{2}−15\sqrt{4}\)

Simplify, then combine like terms.

\(8−20\sqrt{2}+6\sqrt{2}−15\sqrt{4}=8−20\sqrt{2}+6\sqrt{2}−30=−22−14\sqrt{2}\)

Check.

Exercise \(\PageIndex{52}\)

\((3+5\sqrt{3})(1−2\sqrt{3})\)

Exercise \(\PageIndex{53}\)

\((2+3\sqrt{2})(2−3\sqrt{2})\)

Answer

Here we use the difference of squares pattern: \((a+b)(a−b) = a^2−b^2\).

\((2+3\sqrt{2})(2−3\sqrt{2}) = (2)^2−(3\sqrt{2})^2\)

Recall that \((ab)^2 = a^{2}b^2\).

\((2)^2 −(3\sqrt{2})^2 =4−(3)^{2}(\sqrt{2})^2 = 4−9 \cdot 2 = 4−18 = −14\)

Check.

Exercise \(\PageIndex{54}\)

\((3 + 2\sqrt{5})(3 − 2\sqrt{5})\)

Exercise \(\PageIndex{55}\)

\((2\sqrt{3}+3\sqrt{2})(2\sqrt{3}−3\sqrt{2})\)

Answer

Here we use the difference of squares pattern: \((a+b)(a−b) = a^2−b^2\).

\((2\sqrt{3}+3\sqrt{2})(2\sqrt{3}−3\sqrt{2}) = (2\sqrt{3})^2−(3\sqrt{2})^2\)

Recall that \((ab)^2 = a^{2}b^2\).

\((2\sqrt{3})^2 −(3\sqrt{2})^2 =(2)^2(\sqrt{3})^2−(3)^{2}(\sqrt{2})^2 = 4 \cdot 3−9 \cdot 2 = 12−18 = −6\)

Check.

Exercise \(\PageIndex{56}\)

\((8\sqrt{2}+\sqrt{5})(8\sqrt{2}−\sqrt{5})\)

Exercise \(\PageIndex{57}\)

\((2+\sqrt{5})^2\)

Answer

Here we use the squaring a binomial pattern: \((a+b)^2 = a^2+2ab+b^2\).

Recall that \((ab)^2 = a^{2}b^2\).

\((2+\sqrt{5})^2 = (2)^2+2(2)(\sqrt{5})+(\sqrt{5})^2 = 4+4\sqrt{5}+5 = 9+4\sqrt{5}\)

Check.

Exercise \(\PageIndex{58}\)

\((3−\sqrt{2})^2\)

Exercise \(\PageIndex{59}\)

\((\sqrt{3}−2\sqrt{5})^2\)

Answer

Here we use the squaring a binomial pattern: \((a−b)^2 = a^2−2ab+b^2\).

Recall that \((ab)^2 = a^{2}b^2\).

\((\sqrt{3}−2\sqrt{5})^2 = (\sqrt{3})^2−2(\sqrt{3})(2\sqrt{5})+(2\sqrt{5})^2 = 3−4\sqrt{15}+ 4 \cdot 5 = 3−4\sqrt{15}+20 = 23−4\sqrt{15}\)

Check.

Exercise \(\PageIndex{60}\)

\((2\sqrt{3} + 3\sqrt{2})^2\)

In Exercises 61-68, place each of the given rational expressions in simple radical form by “rationalizing the denominator.” Check your result with your calculator.

Exercise \(\PageIndex{61}\)

\(\frac{1}{\sqrt{5}+\sqrt{3}}\)

Answer

Multiply numerator and denominator by \(\sqrt{5}−\sqrt{3}\). Recall the difference of squares pattern: \((a+b)(a−b)=a^2−b^2\).

\(\frac{1}{\sqrt{5}+\sqrt{3}} = \frac{1}{\sqrt{5}+\sqrt{3}} \cdot \frac{\sqrt{5}−\sqrt{3}}{\sqrt{5}−\sqrt{3}} = \frac{\sqrt{5}−\sqrt{3}}{(\sqrt{5})^2−(\sqrt{3})^2}\)

Continuing.

\(\frac{\sqrt{5}−\sqrt{3}}{(\sqrt{5})^2−(\sqrt{3})^2} = \frac{\sqrt{5}−\sqrt{3}}{5−3} = \frac{\sqrt{5}−\sqrt{3}}{2}\)

Check.

Exercise \(\PageIndex{62}\)

\(\frac{1}{2\sqrt{3}−2}\)

Exercise \(\PageIndex{63}\)

\(\frac{6}{2\sqrt{5}−\sqrt{2}}\)

Answer

Multiply numerator and denominator by \(2\sqrt{5}+\sqrt{2}\). Recall the difference of squares pattern: \((a+b)(a−b)=a^2−b^2\).

\(\frac{6}{2\sqrt{5}−\sqrt{2}} = \frac{6}{2\sqrt{5}−\sqrt{2}} \cdot \frac{2\sqrt{5}+\sqrt{2}}{2\sqrt{5}+\sqrt{2}} = \frac{12\sqrt{5}+6\sqrt{2}}{(2\sqrt{5})^2−(\sqrt{2})^2}\)

Continuing.

\(\frac{12\sqrt{5}+6\sqrt{2}}{(2\sqrt{5})^2−(\sqrt{2})^2} = \frac{12\sqrt{5}+6\sqrt{2}}{20−2} = \frac{12\sqrt{5}−6\sqrt{2}}{18}\).

Reduce. Factor the numerator and denominator and cancel.

\(\frac{12\sqrt{5}−6\sqrt{2}}{18} = \frac{6(2\sqrt{5}−\sqrt{2})}{6 \cdot 3} = \frac{2\sqrt{5}−\sqrt{2}}{3}\).

Check.

Exercise \(\PageIndex{64}\)

\(\frac{9}{3\sqrt{3}−\sqrt{6}}\)

Exercise \(\PageIndex{65}\)

\(\frac{2+\sqrt{3}}{2−\sqrt{3}}\)

Answer

Multiply numerator and denominator by \(2+\sqrt{3}\).

\(\frac{2+\sqrt{3}}{2−\sqrt{3}} = \frac{2+\sqrt{3}}{2−\sqrt{3}} \cdot \frac{2+\sqrt{3}}{2+\sqrt{3}} = \frac{(2+\sqrt{3})^2}{(2−\sqrt{3})(2−\sqrt{3})}\).

Use the squaring a binomial pattern \((a+b)^2 = a^2+2ab+b^2\) on the numerator and the difference of squares pattern \((a+b)(a−b) = a^2−b^2\) on the denominator.

\(\frac{(2+\sqrt{3})^2}{(2−\sqrt{3})(2−\sqrt{3})} = \frac{(2)^2+2(2)(\sqrt{3})+(\sqrt{3})^2}{2^2−(\sqrt{3})^2}\).

Continuing.

\(\frac{(2)^2+2(2)(\sqrt{3})+(\sqrt{3})^2}{2^2−(\sqrt{3})^2} = \frac{4+4\sqrt{3}+3}{4−3} = 7+4\sqrt{3}\)

Check.

Exercise \(\PageIndex{66}\)

\(\frac{3−\sqrt{5}}{3+\sqrt{5}}\)

Exercise \(\PageIndex{67}\)

\(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}}\)

Answer

Multiply numerator and denominator by \(\sqrt{3}+\sqrt{2}\).

\(\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}} = \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}} \cdot \frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}} = \frac{(\sqrt{3}+\sqrt{2})^2}{(\sqrt{3}−\sqrt{2})(\sqrt{3}+\sqrt{2})}\).

Use the squaring a binomial pattern \((a+b)^2 = a^2+2ab+b^2\) on the numerator and the difference of squares pattern \((a+b)(a−b) = a^2−b^2\) on the denominator.

\(\frac{(\sqrt{3}+\sqrt{2})^2}{(\sqrt{3}−\sqrt{2})(\sqrt{3}+\sqrt{2})}= \frac{(\sqrt{3})^2+2(\sqrt{3})(\sqrt{2})+(\sqrt{2})^2}{(\sqrt{3})^2−(\sqrt{2})^2}\).

Continuing.

\(\frac{(\sqrt{3})^2+2(\sqrt{3})(\sqrt{2})+(\sqrt{2})^2}{(\sqrt{3})^2−(\sqrt{2})^2} = \frac{3+2\sqrt{6}+2}{3−2} = 5+2\sqrt{6}\)

Check.

Exercise \(\PageIndex{68}\)

\(\frac{2\sqrt{3}+\sqrt{2}}{\sqrt{3}−\sqrt{2}}\)

In Exercises 69-76, use the quadratic formula to find the solutions of the given equation. Place your solutions in simple radical form and reduce your solutions to lowest terms.

Exercise \(\PageIndex{69}\)

\(3x^2−8x=5\)

Answer

The equation is nonlinear, so make one side zero.

\(3x^2−8x−5=0\)

Compare \(3x^2−8x−5 = 0\) with \(ax^2+bx+c = 0\) and note that a = 3, b = −8, and c = −5. Write down the quadratic formula and substitute.

\(x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−8) \pm \sqrt{��(−8)^2 −4(3)(−5)}}{2(3)} = \frac{8 \pm \sqrt{124}}{6}\)

Factor a perfect square from the radical in the numerator.

\(x = \frac{8 \pm \sqrt{4}\sqrt{31}}{6} = \frac{8 \pm 2\sqrt{31}}{6}\)

Factor the numerator and cancel.

\(x = \frac{8 \pm 2\sqrt{31}}{6} = \frac{2(4 \pm \sqrt{31})}{2 \cdot 3} = \frac{4 \pm \sqrt{31}}{3}\)

Exercise \(\PageIndex{70}\)

\(5x^2−2x=1\)

Exercise \(\PageIndex{71}\)

\(5x^2=2x+1\)

Answer

The equation is nonlinear, so make one side zero.

\(5x^2−2x−1=0\)

Compare \(5x^2−2x−1 = 0\) with \(ax^2+bx+c = 0\) and note that a = 5, b = −2, and c = −1. Write down the quadratic formula and substitute.

\(x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−2) \pm \sqrt{��(−2)^2 −4(5)(−1)}}{2(5)} = \frac{2 \pm \sqrt{24}}{10}\)

Factor a perfect square from the radical in the numerator.

\(x = \frac{2 \pm \sqrt{4}\sqrt{6}}{10} = \frac{2 \pm 2\sqrt{6}}{10}\)

Factor the numerator and cancel.

\(x = \frac{2 \pm 2\sqrt{6}}{10} = \frac{2(1 \pm \sqrt{6})}{2 \cdot 5} = \frac{1 \pm \sqrt{6}}{5}\)

Exercise \(\PageIndex{72}\)

\(3x^2−2x=11\)

Exercise \(\PageIndex{73}\)

\(7x^2=6x+2\)

Answer

The equation is nonlinear, so make one side zero.

\(7x^2−6x−2=0\)

Compare \(7x^2−6x−2 = 0\) with \(ax^2+bx+c = 0\) and note that a = 7, b = −6, and c = −2. Write down the quadratic formula and substitute.

\(x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−6) \pm \sqrt{��(−6)^2 −4(7)(−2)}}{2(7)} = \frac{6 \pm \sqrt{92}}{14}\)

Factor a perfect square from the radical in the numerator.

\(x = \frac{6 \pm \sqrt{4}\sqrt{23}}{14} = \frac{6 \pm 2\sqrt{23}}{14}\)

Factor the numerator and cancel.

\(x = \frac{6 \pm 2\sqrt{23}}{14} = \frac{2(3 \pm \sqrt{23})}{2 \cdot 7} = \frac{6 \pm \sqrt{23}}{7}\)

Exercise \(\PageIndex{74}\)

\(11x^2+6x=4\)

Exercise \(\PageIndex{75}\)

\(x^2=2x+19\)

Answer

The equation is nonlinear, so make one side zero.

\(x^2−2x−19=0\)

Compare \(x^2−2x−19 = 0\) with \(ax^2+bx+c = 0\) and note that a = 1, b = −2, and c = −19. Write down the quadratic formula and substitute.

\(x = \frac{−b \pm \sqrt{b^2−4ac}}{2a} = \frac{−(−2) \pm \sqrt{��(−2)^2 −4(1)(−19)}}{2(1)} = \frac{2 \pm \sqrt{80}}{2}\)

Factor a perfect square from the radical in the numerator.

\(x = \frac{2 \pm \sqrt{16}\sqrt{5}}{2} = \frac{2 \pm 4\sqrt{5}}{2}\)

Factor the numerator and cancel.

\(x = \frac{2 \pm 4\sqrt{5}}{2} = \frac{2(1 \pm 2\sqrt{5})}{2 \cdot 1} = 1 \pm 2\sqrt{5}\)

Exercise \(\PageIndex{76}\)

\(100x^2=40x−1\)

In Exercises 77-80, we will suspend the usual rule that you should rationalize the denominator. Instead, just this one time, rationalize the numerator of the resulting expression.

Exercise \(\PageIndex{77}\)

Given \(f(x) = \sqrt{x}\), evaluate the expression \(\frac{f(x)−f(2)}{x−2}\), and then “rationalize the numerator.”

Answer

If \(f(x) = \sqrt{x}\), then

\(\frac{f(x)−f(2)}{x−2} = \frac{\sqrt{x}−\sqrt{2}}{x−2}\).

To “rationalize the numerator,” multiply numerator and denominator by \(\sqrt{x}+\sqrt{2}\), then use the difference of squares pattern to simplify.

\(\frac{\sqrt{x}−\sqrt{2}}{x−2} = \frac{\sqrt{x}−\sqrt{2}}{x−2} \cdot \frac{\sqrt{x}+\sqrt{2}}{\sqrt{x}+\sqrt{2}} = \frac{(\sqrt{x})^2−(\sqrt{2})^2}{(x−2)(\sqrt{x}+\sqrt{2})} = \frac{x−2}{(x−2)(\sqrt{x}+\sqrt{2})}\)

Numerator and denominator are factored, so we can cancel,

\(\frac{x−2}{(x−2)(\sqrt{x}+\sqrt{2})} = \frac{1}{\sqrt{x}+\sqrt{2}}\),

provided, of course, that \(x \ne 2\).

Exercise \(\PageIndex{78}\)

Given \(f(x) = \sqrt{x+2}\), evaluate the expression \(\frac{f(x)−f(3)}{x−3}\), and then “rationalize the numerator.”

Exercise \(\PageIndex{79}\)

Given \(f(x) = \sqrt{x}\), evaluate the expression \(\frac{f(x+h)−f(x)}{h}\), and then “rationalize the numerator.”

Answer

If \(f(x) = \sqrt{x}\), then

\(\frac{f(x+h)−f(x)}{h} = \frac{\sqrt{x+h}−\sqrt{x}}{h}\)

To “rationalize the numerator,” multiply numerator and denominator by \(\sqrt{x+h}+\sqrt{x}\), then use the difference of squares pattern to simplify.

\(\frac{\sqrt{x+h}−\sqrt{x}}{h} = \frac{\sqrt{x+h}−\sqrt{x}}{h} \cdot \frac{\sqrt{x+h}+\sqrt{x}}{\sqrt{x+h}+\sqrt{x}} = \frac{(\sqrt{x+h})^2−(\sqrt{x})^2}{h(\sqrt{x+h}+\sqrt{x})} = \frac{x+h−x}{h(\sqrt{x+h}+\sqrt{x})}\)

Simplify, then cancel.

\(\frac{x+h−x}{h(\sqrt{x+h}+\sqrt{x})} = \frac{h}{h(\sqrt{x+h}+\sqrt{x})} = \frac{1}{\sqrt{x+h}+\sqrt{x}}\)

The result is valid provided \(h \ne 0\).

Exercise \(\PageIndex{80}\)

Given \(f(x) = \sqrt{x−3}\), evaluate the expression \(\frac{f(x+h)−f(x)}{h}\), and then “rationalize the numerator.”