9.2: Multiplication Properties of Radicals
- Page ID
- 19735
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
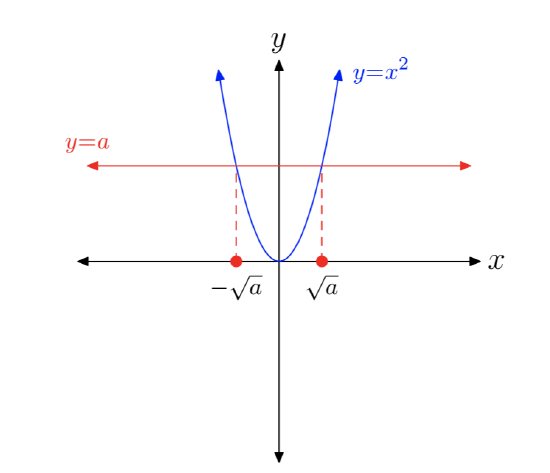
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Recall that the equation \(x^2 = a\), where a is a positive real number, has two solutions, as indicated in Figure 1.
Here are the key facts.
Solutions of \(x^2 = a\). If a is a positive real number, then:
- The equation \(x^2 = a\) has two real solutions.
- The notation \(\sqrt{a}\) denotes the unique positive real solution.
- The notation \(−\sqrt{a}\) denotes the unique negative real solution.
Note the use of the word unique. When we say that solution \(\sqrt{a}\) is the unique positive real solution, we mean that it is the only one. There are no other positive real numbers that are solutions of \(x^2 = a\). A similar statement holds for the unique negative solution.
Thus, the equations \(x^2 = a\) and \(x^2 = b\) have unique positive solutions \(x = \sqrt{a}\) and \(x = \sqrt{b}\), respectively, provide that a and b are positive real numbers. Furthermore, because they are solutions, they can be substituted into the equations \(x^2 = a\) and \(x^2 = b\) to produce the results
\((\sqrt{a})^2 = a\) and \((\sqrt{b})^2 = b\)
respectively. Again, these results are dependent upon the fact that a and b are positive real numbers.
Similarly, the equation
\(x^2 = ab\)
has unique positive solution \(x = \sqrt{ab}\), provided a and b are positive numbers. However, note that
\((\sqrt{a}\sqrt{b})^2 = (\sqrt{a})^{2}(\sqrt{b})^{2} = ab\),
making \(\sqrt{a}\sqrt{b}\) a second positive solution of \(x^2 = ab\). However, because \(\sqrt{ab}\) is the unique positive solution of \(x^2 = ab\), this forces
\(\sqrt{ab} = \sqrt{a}\sqrt{b}\)
This discussion leads to the following property of radicals.
Let \(a\) and \(b\) be positive real numbers. Then,
\[\sqrt{ab} = \sqrt{a}\sqrt{b} \nonumber \]
This result can be used in two distinctly different ways.
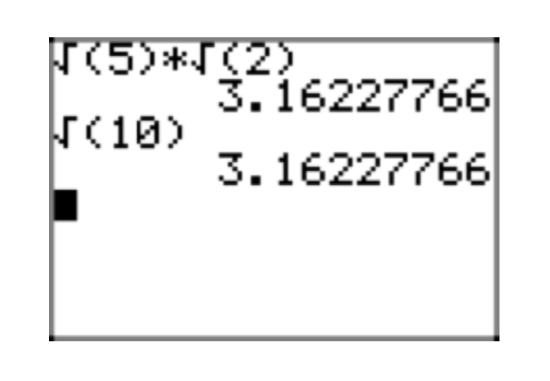
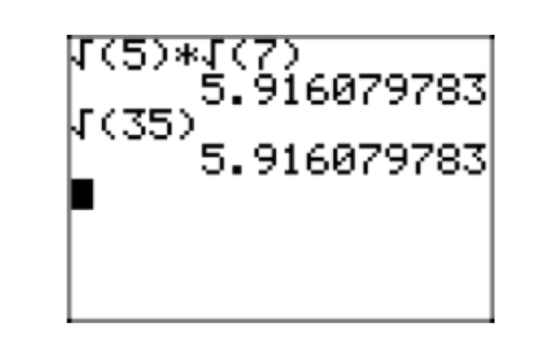
- You can use the result to multiply two square roots, as in
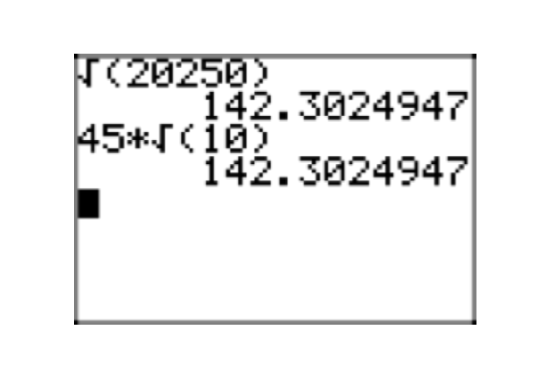
\(\sqrt{7}\sqrt{5} = \sqrt{35}\).
- \(\sqrt{35} = \sqrt{7}\sqrt{5}\)
It is interesting to check this result on the calculator, as shown in Figure 2.
Simple Radical Form
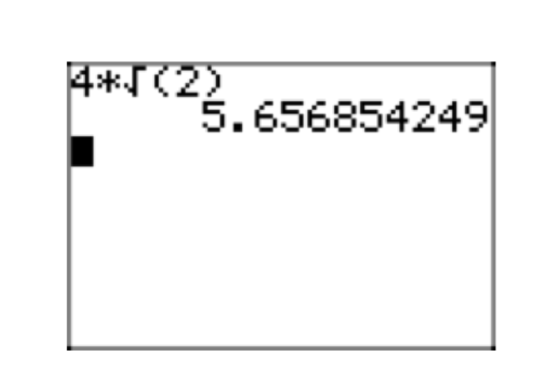
In this section we introduce the concept of simple radical form, but let’s first start with a little story. Martha and David are studying together, working a homework problem from their textbook. Martha arrived at an answer of \(\sqrt{32}\), while David gets the result \(2\sqrt{8}\). At first, David and Martha believe that their solutions are different numbers, but they’ve been mistaken before so they decide to compare decimal approximations of their results on their calculators. Martha’s result is shown in Figure 3(a), while David’s is shown Figure 3(b).

Martha finds that \(\sqrt{32} \approx 5.656854249\) and David finds that his solution \(2\sqrt{8} \approx 5.656854249\). David and Martha conclude that their solutions match, but they want to know why the two very different looking radical expressions are identical.
The following calculation, using Property 1, shows why David’s result is identical to Martha’s.
\(\sqrt{32}=\sqrt{4}\sqrt{8}=2\sqrt{8}\)
Indeed, there is even a third possibility, one that is much different from the results found by David and Martha. Consider the following calculation, which again uses Property 1.
\(\sqrt{32}=\sqrt{16}\sqrt{2}=4\sqrt{2}\)
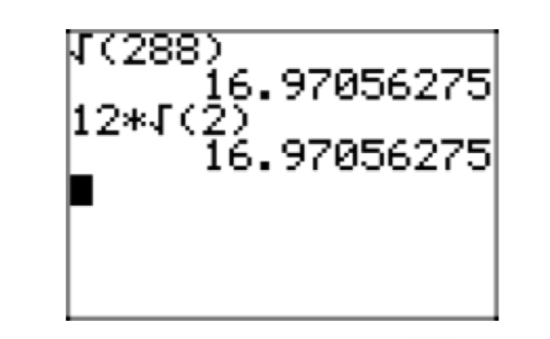
In Figure 4, note that the decimal approximation of \(4\sqrt{2}\) approximations for \(\sqrt{32}\) (Martha’s result in Figure 3(a)) and \(2\sqrt{8}\) (David’s result inFigure 3(b)).
While all three of these radical expressions (\(\sqrt{32}\), \(2\sqrt{8}\), and \(4\sqrt{2}\)) are identical, it is somewhat frustrating to have so many different forms, particularly when we want to compare solutions. Therefore, we offer a set of guidelines for a special form of the answer which we will call simple radical form.
When possible, factor out a perfect square.
Thus, \(\sqrt{32}\) is not in simple radical form, as it is possible to factor out a perfect square, as in
\(\sqrt{32}=\sqrt{16}\sqrt{2}=4\sqrt{2}\).
Similarly, David’s result \((2\sqrt{8})\) is not in simple radical form, because he too can factor out a perfect square as follows.
\(2\sqrt{8}=2(\sqrt{4}\sqrt{2})=2(2\sqrt{2})=(2 \cdot 2)\sqrt{2}=4\sqrt{2}\).
If both Martha and David follow the “first guideline for simple radical form,” their answer will look identical (both equal \(4\sqrt{2}\)). This is one of the primary advantages of simple radical form: the ability to compare solutions.
In the examples that follow (and in the exercises), it is helpful if you know the squares of the first 25 positive integers. We’ve listed them in the margin for you in Table 1 for future reference.
Let’s place a few more radical expressions in simple radical form.

Place \(\sqrt{50}\) in simple radical form.
- Answer
-
In Table 1, 25 is a square. Because \(50 = 25 \cdot 2\), we can use Property 1 to write
\(\sqrt{50}=\sqrt{25}\sqrt{2}=5\sqrt{2}\).
Place \(\sqrt{98}\) in simple radical form.
- Answer
-
In Table 1, 49 is a square. Because \(98 = 49 \cdot 2\), we can use Property 1 to write
\(\sqrt{98}=\sqrt{49}\sqrt{2}=7\sqrt{2}\).
Place \(\sqrt{288}\) in simple radical form.
- Answer
-
Some students seem able to pluck the optimal “perfect square” out of thin air. If you consult Table 1, you’ll note that 144 is a square. Because \(288 = 144 \cdot 2\), we can write
\(\sqrt{288}=\sqrt{144}\sqrt{2}=12\sqrt{2}\).
However, what if you miss that higher perfect square, think \(288 = 4 \cdot 72\), and write
\(\sqrt{288}=\sqrt{4}\sqrt{72}=2\sqrt{72}\).
This approach is not incorrect, provided you realize that you’re not finished. You can still factor a perfect square out of 72. Because \(72 = 36 \cdot 2\), you can continue and write
\(2\sqrt{72}=2(\sqrt{36}\sqrt{2})=2(6\sqrt{2})=(2\cdot 6)\sqrt{2}=12\sqrt{2}\).
Note that we arrived at the same simple radical form, namely \(12\sqrt{2}\). It just took us a little longer. As long as we realize that we must continue until we can no longer factor out a perfect square, we’ll arrive at the same simple radical form as the student who seems to magically pull the higher square out of thin air.
Indeed, here is another approach that is equally valid.
\(\sqrt{288}=\sqrt{4}\sqrt{72}=2(\sqrt{4}\sqrt{18})=2(2\sqrt{18})=(2\cdot 2)\sqrt{18}=4\sqrt{18}\)
We need to recognize that we are still not finished because we can extract another perfect square as follows.
\(4\sqrt{18}=4(\sqrt{9}\sqrt{2})=4(3\sqrt{2})=(4\cdot 3)\sqrt{2}=12\sqrt{2}\)
Once again, same result. However, note that it behooves us to extract the largest square possible, as it minimizes the number of steps required to attain simple radical form.
Checking Results with the Graphing Calculator. Once you’ve placed a radical expression in simple radical form, you can use your graphing calculator to check your result. In this example, we found that
\(\sqrt{288}=12\sqrt{2}\). (6)
Enter the left- and right-hand sides of this result as shown in Figure 5. Note that each
side produces the same decimal approximation, verifying the result in equation (6).
Helpful Hints
Recall that raising a power of a base to another power requires that we multiply exponents.
\((a^m)^n = a^{mn}\)
In particular, when you square a power of a base, you must multiply the exponent by 2. For example,
\((2^5)^2 = 2^{10}\).
Conversely, because taking a square root is the “inverse” of squaring, when taking a square root we must divide the existing exponent by 2, as in
\(\sqrt{2^{10}} = 2^5\).
Note that squaring \(2^5\) gives \(2^{10}\), so taking the square root of \(2^{10}\) must return you to \(2^5\). When you square, you double the exponent. Therefore, when you take the square root, you must halve the exponent.
Similarly,
- \((2^6)^2 = 2^{12}\) so \(\sqrt{2^{12}} = 2^6\).
- \((2^7)^2 = 2^{14}\) so \(\sqrt{2^{14}} = 2^7\).
- \((2^8)^2 = 2^{16}\) so \(\sqrt{2^{16}} = 2^8\).
This leads to the following result.
When taking a square root of \(x^n\), when x is a positive real number and n is an even natural number, divide the exponent by two. In symbols,
\(\sqrt{x^n} = x^{\frac{n}{2}}\).
Note that this agrees with the definition of rational exponents presented in Chapter 8, as in
\(\sqrt{x^n} = (x^n)^{\frac{1}{2}} = x^{\frac{n}{2}}\).
On another note, recall that raising a product to a power requires that we raise each factor to that power.
\((ab)^n = a^{n}b^{n}\).
In particular, if you square a product, you must square each factor. For example,
\((5^{3}7^{4})^2 = (5^3)^{2}(7^4)^2 = 5^{6}7^{8}\).
Note that we multiplied each existing exponent in this product by 2.
Property 1 is similar, in that when we take the square root of a product, we take the square root of each factor. Because taking a square root is the inverse of squaring, we must divide each existing exponent by 2, as in
\(\sqrt{5^{6}7^{8}} = \sqrt{5^{6}}\sqrt{7^{8}} = 5^{3}7^{4}\)
Let’s look at some examples that employ this technique.
Simplify \(\sqrt{2^{4}3^{6}5^{10}}\)
- Answer
-
When taking the square root of a product of exponential factors, divide each exponent by 2.
\(\sqrt{2^{4}3^{6}5^{10}} = 2^{2}3^{3}5^{5}\)
If needed, you can expand the exponential factors and multiply to provide a single numerical answer.
\(2^{2}3^{3}5^{5} = 4 \cdot 27 \cdot 3125 = 337500\)
A calculator was used to obtain the final solution.
Simplify \(\sqrt{2^{5}3^{3}}\)
- Answer
-
In this example, the difficulty is the fact that the exponents are not divisible by 2. However, if possible, the “first guideline of simple radical form” requires that we factor out a perfect square. So, extract each factor raised to the highest possible power that is divisible by 2, as in
\(\sqrt{2^{5}3^{3}} = \sqrt{2^{4}3^{2}}\sqrt{2 \cdot 3}\)
Now, divide each exponent by 2.
\(\sqrt{2^{4}3^{2}}\sqrt{2\cdot 3} = 2^{2}3^{1}\sqrt{2 \cdot 3}\)
Finally, simplify by expanding each exponential factor and multiplying.
\(2^{2}3^{1}\sqrt{2 \cdot 3} = 4 \cdot 3\sqrt{2 \cdot 3} = 12\sqrt{6}\)
Simplify \(\sqrt{3^{7}5^{2}7^{5}}\).
- Answer
-
Extract each factor to the highest possible power that is divisible by 2.
\(\sqrt{3^{7}5^{2}7^{5}} = \sqrt{3^{6}5^{2}7^{4}}\sqrt{3 \cdot 7}\)
Divide each exponent by 2.
\(\sqrt{3^{6}5^{2}7^{4}}\sqrt{3 \cdot 7} = 3^{3}5^{1}7^{2}\sqrt{3 \cdot 7}\)
Expand each exponential factor and multiply.
\(3^{3}5^{1}7^{2}\sqrt{3 \cdot 7} = 27 \cdot 5 \cdot 49 \sqrt{3 \cdot 7} =6615\sqrt{21}\)
Place \(\sqrt{216}\) in simple radical form.
If we prime factor 216, we can attack this problem with the same technique used in the previous examples. Before we prime factor 216, here are a few divisibility tests that you might find useful.
- If a number ends in 0, 2, 4, 6, or 8, it is an even number and is divisible by 2.
- If the last two digits of a number form a number that is divisible by 4, then the entire number is divisible by 4.
- If a number ends in 0 or 5, it is divisible by 5.
- If the sum of the digits of a number is divisible by 3, then the entire number is divisible by 3.
- If the sum of the digits of a number is divisible by 9, then the entire number is divisible by 9.
For example, in order:
- The number 226 ends in a 6, so it is even and divisible by 2. Indeed, \(226 = 2 \cdot 113\).
- The last two digits of 224 are 24, which is divisible by 4, so the entire number is divisible by 4. Indeed, \(224 = 4 \cdot 56\).
- The last digit of 225 is a 5. Therefore 225 is divisible by 5. Indeed, \(225 = 5 \cdot 45\).
- The sum of the digits of 222 is 2 + 2 + 2 = 6, which is divisible by 3. Therefore, 222 is divisible by 3. Indeed, \(222 = 3 \cdot 74\).
- The sum of the digits of 684 is 6 + 8 + 4 = 18, which is divisible by 9. Therefore, 684 is divisible by 9. Indeed, \(684 = 9 \cdot 76\).
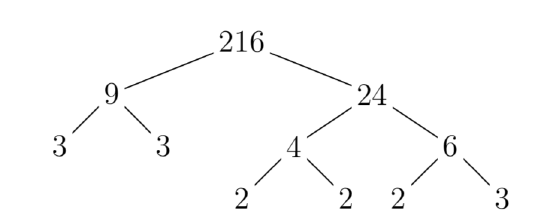
Now, let’s prime factor 216. Note that 2+1+6 = 9, so 216 is divisible by 9. Indeed, \(216 = 9 \cdot 24\). In Figure 6, we use a “factor tree” to continue factoring until all of the “leaves” are prime numbers.
Thus,
\(216 = 2 \cdot 2 \cdot 2 \cdot 3 \cdot 3 \cdot 3\),
or in exponential form,
\(216 = 2^{3} \cdot 3^{3}\).
Thus,
\(\sqrt{216} = \sqrt{2^{3}3^{3}} = \sqrt{2^{2}3^{2}}\sqrt{2\cdot 3}=2 \cdot 3\sqrt{2 \cdot 3}=6\sqrt{6}\).
Prime factorization is an unbelievably useful tool!
Let’s look at another example.
Place \(\sqrt{2592}\) in simple radical form.
- Answer
-
If we find the prime factorization for 2592, we can attack this example using the same technique we used in the previous example. We note that the sum of the digits of 2592 is 2 + 5 + 9 + 2 = 18, which is divisible by 9. Therefore, 2592 is also divisible by 9.
\(2592 = 9 \cdot 288\)
The sum of the digits of 288 is 2+8+8 = 18, which is divisible by 9, so 288 is also divisible by 9.
\(2592 = 9 \cdot (9 \cdot 32)\)
Continue in this manner until the leaves of your “factor tree” are all primes. Then, you should get
\(2592 = 2^{5}3^{4}\).
Thus,
\(\sqrt{2592} = \sqrt{2^{5}3^{4}} = \sqrt{2^{4}3^{4}}\sqrt{2} = 2^{2}3^{2}\sqrt{2} = 4 \cdot 9\sqrt{2}=36\sqrt{2}\).
Let’s use the graphing calculator to check this result. Enter each side of \(\sqrt{2592} = 36\sqrt{2}\) separately and compare approximations, as shown in Figure 7.
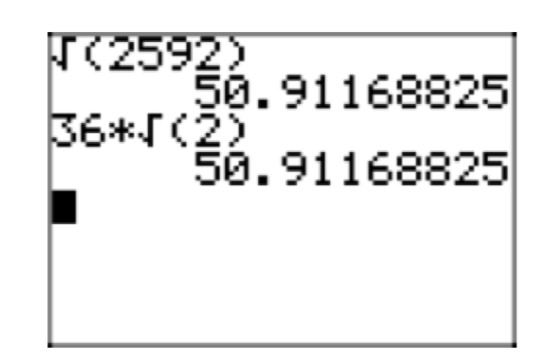
Figure 7. Comparing \(\sqrt{2592}\) with its simple radical form \(36\sqrt{2}\).
An Important Property of Square Roots
One of the most common mistakes in algebra occurs when practitioners are asked to simplify the expression \(\sqrt{x^2}\), where x is any arbitrary real number. Let’s examine two of the most common errors.
- Some will claim that the following statement is true for any arbitrary real number x.
\(\sqrt{x^2} = \pm x\).
This is easily seen to be incorrect. Simply substitute any real number for x to check this claim. We will choose x = 3 and substitute it into each side of the proposed statement.
\(\sqrt{3^2} = \pm 3\).
If we simplify the left-hand side, we produce the following result.
\(\sqrt{3^2} = \pm 3\).
\(3 = \pm 3\)
It is not correct to state that 3 and \(\pm 3\) are equal.
- A second error is to claim that
\(\sqrt{x^2} = x\)
for any arbitrary real number x. Although this is certainly true if you substitute nonnegative numbers for x, look what happens when you substitute −3 for x.
\(\sqrt{(−3)^2} = 3\)
If we simplify the left-hand side, we produce the following result.
\(\sqrt{9} = −3\)
3 = −3
Clearly, 3 and −3 are not equal.
In both cases, what has been forgotten is the fact that \(\sqrt{}\) calls for a positive (nonnegative if you want to include the case \(\sqrt{0}\)) square root. In both of the errors above, namely \(\sqrt{x^2} = \pm x\) and \(\sqrt{x^2} = x\), the left-hand side is calling for a nonnegative response, but nothing has been done to insure that the right-hand side is also nonnegative. Does anything come to mind?
Sure, if we wrap the right-hand side in absolute values, as in
\(\sqrt{x^2} = |x|\),
then both sides are calling for a nonnegative response. Indeed, note that
\(\sqrt{(−3)^2} =|−3|\), \(\sqrt{0^2} =|0|\), and \(\sqrt{3^2} =|3|\)
are all valid statements.
This discussion leads to the following result.
If x is any real number, then
\(\sqrt{x^2} = |x|\),
The next task is to use this new property to produce a extremely useful property of absolute value.
A Multiplication Property of Absolute Value
If we combine the law of exponents for squaring a product with our property for taking the square root of a product, we can write
\(\sqrt{(ab)^2} = \sqrt{a^{2}b^{2}} = \sqrt{a^2}\sqrt{b^2}\).
However, \(\sqrt{(ab)^2} = |ab|\), while \(\sqrt{a^2}{b^2} = |a||b|\). This discussion leads to the following result.
If a and b are any real numbers,
|ab| = |a||b|.
In words, the absolute value of a product is equal to the product of the absolute values.
We saw this property previously in the chapter on the absolute value function, where we provided a different approach to the proof of the property. It’s interesting that we can prove this property in a completely new way using the properties of square root. We’ll see we have need for the Product Rule for Absolute Value in the examples that follow.
For example, using the product rule, if x is any real number, we could write
|3x| = |3||x| = 3|x|
However, there is no way we can remove the absolute value bars that surround x unless we know the sign of x. If \(x \ge 0\), then |x| = x and the expression becomes
3|x| = 3x.
On the other hand, if x < 0, then |x| = −x and the expression becomes
3|x| = 3(−x) = −3x.
Let’s look at another example. Using the product rule, if x is any real number, the expression \(| − 4x^3|\) can be manipulated as follows.
\(|−4x^3| = |−4||x^2||x|\)
However,|−4|=4 and since \(x^2 \ge 0\) for any value of x, \(|x^2|=x^2\). Thus,
\(|−4||x^2||x| = 4x^{2}|x|\).
Again, there is no way we can remove the absolute value bars around x unless we know the sign of x. If \(x \ge 0\), then|x|=x and
\(4x^{2}|x| = 4x^{2}(x) = 4x^3\).
On the other hand, if x < 0, then |x| = −x and
\(4x^{2}|x| = 4x^{2}(−x) = −4x^3\).
Let’s use these ideas to simplify some radical expressions that contain variables.
Variable Expressions
Given that the x represents any real numbers, place the radical expression
\(\sqrt{48x^6}\)
in simple radical form.
Simple radical form demands that we factor out a perfect square, if possible. In this case, \(48 = 16 \cdot 3\) and we factor out the highest power of x that is divisible by 2.
\(\sqrt{48x^6} = \sqrt{16x^6}\sqrt{3}\)
We can now use Property 1 to take the square root of each factor.
\(\sqrt{16x^6}\sqrt{3} = \sqrt{16}\sqrt{x^6}\sqrt{3}\)
Now, remember the notation \(\sqrt{}\) calls for a nonnegative square root, so we must insure that each response in the equation above is nonnegative. Thus,
\(\sqrt{16}\sqrt{x^6}\sqrt{3} = 4|x^3|\sqrt{3}\)
Some comments are in order.
- The nonnegative square root of 16 is 4. That is, \(\sqrt{16} = 4\)
- The nonnegative square root of x6 is trickier. It is incorrect to say \(\sqrt{x^6} = x^3\), because \(x^3\) could be negative (if x is negative). To insure a nonnegative square root, in this case we need to wrap our answer in absolute value bars. That is, \(\sqrt{x^6} = |x^3|\).
We can use the Product Rule for Absolute Value to write \(|x^3| = |x^2||x|\). Because \(x^2\) is nonnegative, absolute value bars are redundant and not needed. That is, \(|x^2||x| = x^{2}|x|\). Thus, we can simplify our solution a bit further and write
\(4|x^3|\sqrt{3} = 4x^{2}|x|\sqrt{3}\)
Thus,
\(\sqrt{48x^6} = 4x^{2}|x|\sqrt{3}\).
Alternate Solution. There is a variety of ways that we can place a radical expression in simple radical form. Here is another approach. Starting at the step above, where we first factored out a perfect square,
\(\sqrt{48x^6} = \sqrt{16x^6}\sqrt{3}\)
we could write
\(\sqrt{16x^6}\sqrt{3} = \sqrt{(4x^3)^2}\sqrt{3}\).
Now, remember that the nonnegative square root of the square of an expression is the absolute value of that expression (we have to guarantee a nonnegative answer), so
\(\sqrt{(4x^3)^2}\sqrt{3} = |4x^3|\sqrt{3}\).
However, \(|4x^3| = |4||x^3|\) by our product rule and \(|4||x^3| = 4|x^3|\). Thus,
\(|4x^3|\sqrt{3} = 4|x^3|\sqrt{3}\).
Finally, \(|x^3| = |x^2||x| = x^2|x|\) because \(x^2 \ge 0\), so we can write
\(4|x^3|\sqrt{3} = 4x^{2}|x|\sqrt{3}\)
We cannot remove the absolute value bar that surrounds x unless we know the sign of x.
Note that the simple radical form in the alternate solution is identical to the simple radical form found with the previous solution technique.
Let’s look at another example.
Given that x < 0, place \(\sqrt{24x^6}\) in simple radical form.
First, factor out a perfect square and write
\(\sqrt{24x^6} = \sqrt{4x^6}\sqrt{6}\)
Now, use Property 1 and take the square root of each factor.
\(\sqrt{4x^6}\sqrt{6}= \sqrt{4}\sqrt{x^6}\sqrt{6}\)
To insure a nonnegative response to \(\sqrt{x^6}\), wrap your response in absolute values.
\(\sqrt{4}\sqrt{x^6}\sqrt{6}=2|x^3|\sqrt{6}\)
However, as in the previous problem, \(|x^3| = |x^2||x| = x^{2}|x|\), since \(x^2 \ge 0\). Thus,
\(2|x^3|\sqrt{6} = 2x^{2}|x|\sqrt{6}\).
In this example, we were given the extra fact that x < 0, so |x| = −x and we can write
\(2x^{2}|x|\sqrt{6} = 2x^{2}(−x)\sqrt{6} = −2x^{3}\sqrt{6}\).
It is instructive to test the validity of the answer
\(\sqrt{24x^6} = −2x^{3}\sqrt{6}\), x<0.
using a calculator.

It is somewhat counterintuitive that the result
\(\sqrt{24x^6} = −2x^{3}\sqrt{6}\), x<0.
contains a negative sign. After all, the expression \(\sqrt{24x^6}\) call for a nonnegative result, but we have a negative sign. However, on closer inspection, if x < 0, then x is a negative number and the right-hand side \(−2x^{3}\sqrt{6}\) is a positive number (−2 is negative, \(x^3\) is negative because x is negative, and the product of two negatives is a positive).
Let’s look at another example.
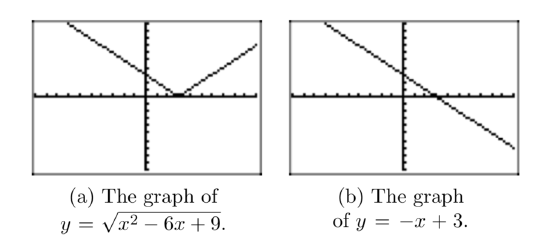
If x < 3,simplify \(\sqrt{x^2−6x+9}\).
The expression under the radical is a perfect square trinomial and factors.
\(\sqrt{x^2−6x+9}=\sqrt{(x−3)^2}\)
However, the nonnegative square root of the square of an expression is the absolute value of that expression, so
\(\sqrt{(x−3)^2} =|x−3|\).
Finally, because we are told that x < 3, this makes x − 3 a negative number, so
|x−3| = −(x−3).
Again, the result \(\sqrt{x^2−6x+9} = −(x−3)\), provided x < 3, is somewhat counterintuitive as we are expecting a positive result. However, if x < 3, the result −(x−3) is positive. You can test this by substituting several values of x that are less than 3 into the expression −(x−3) and noting that the result is positive. For example, if x = 2, then x is less than 3 and
−(x−3) = −(2−3) = −(−1) = 1,
which, of course, is a positive result.
It is even more informative to note that our result is equivalent to
\(\sqrt{x^2−6x+9}=−x+3\), x<3.
This is easily seen by distributing the minus sign in the result −(x−3).
We’ve drawn the graph of \(y = \sqrt{x^2−6x+9}\) on our calculator on Figure 9(a). In Figure 9(b), we’ve drawn the graph of y = −x + 3. Note that the graphs agree when x < 3. Indeed, when you consider the left-hand branch of the “V” in Figure 9(a), you can see that the slope of this branch is −1 and the y-intercept is 3. The equation of this branch is y = −x+3, so it agrees with the graph of y = −x+3 in Figure 9(b) when x is less than 3.
Use a calculator to first approximate \(\sqrt{7}\sqrt{10}\). One the same screen, approximate \(\sqrt{70}\). Report the results on your homework paper.
Use a calculator to first approximate \(\sqrt{5}\sqrt{13}\). One the same screen, approximate \(\sqrt{65}\). Report the results on your homework paper.
In Exercises 5-20, place each of the radical expressions in simple radical form. As in Example 3 in the narrative, check your result with your calculator.
\(\sqrt{18}\)
- Answer
-
\(\sqrt{18} = \sqrt{3^{2} \cdot 2}= \sqrt{3^{2}}\sqrt{2}=3\sqrt{2}\)
\(\sqrt{80}\)
\(\sqrt{112}\)
- Answer
-
\(\sqrt{112} = \sqrt{4^{2} \cdot 7}= \sqrt{4^{2}}\sqrt{7}=4\sqrt{7}\)
\(\sqrt{72}\)
\(\sqrt{108}\)
- Answer
-
\(\sqrt{108} = \sqrt{6^{2} \cdot 3}= \sqrt{6^{2}}\sqrt{3}=6\sqrt{3}\)
\(\sqrt{54}\)
\(\sqrt{50}\)
- Answer
-
\(\sqrt{50} = \sqrt{5^{2} \cdot 2}= \sqrt{5^{2}}\sqrt{2}=5\sqrt{2}\)
\(\sqrt{48}\)
\(\sqrt{245}\)
- Answer
-
\(\sqrt{245} = \sqrt{7^{2} \cdot 5}= \sqrt{7^{2}}\sqrt{5}=7\sqrt{5}\)
\(\sqrt{150}\)
\(\sqrt{98}\)
- Answer
-
\(\sqrt{98} = \sqrt{7^{2} \cdot 2}= \sqrt{7^{2}}\sqrt{2}=7\sqrt{2}\)
\(\sqrt{252}\)
\(\sqrt{45}\)
- Answer
-
\(\sqrt{45} = \sqrt{3^{2} \cdot 5}= \sqrt{3^{2}}\sqrt{5}=3\sqrt{5}\)
\(\sqrt{294}\)
\(\sqrt{24}\)
- Answer
-
\(\sqrt{24} = \sqrt{2^{2} \cdot 6}= \sqrt{2^{2}}\sqrt{6}=2\sqrt{6}\)
\(\sqrt{32}\)
In Exercises 21-26, use prime factorization (as in Example 10 and 11 in the narrative) to assist you in placing the given radical expression in simple radical form. Check your result with your calculator.
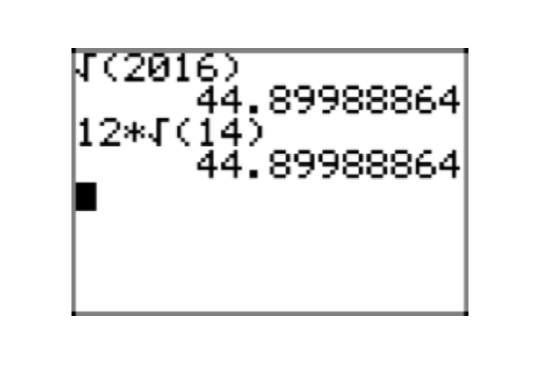
\(\sqrt{2016}\)
- Answer
-
Note that 2+0+1+6 = 9, which is divisible by 9. Thus, 2016 is divisible by 9. Indeed,
\(2019 = 9 \cdot 224\)
The last two digits of 224 are 24, which is divisible by 4. Thus, 224 is divisible by 4. Indeed, \(224 = 4 \cdot 56\).
\(2016 = 9 \cdot 224 = (3 \cdot 3) \cdot (4 \cdot 56)\).
Continue to primes.
\(2016=3 \cdot 3 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 7 = 2^{5} \cdot 3^{2} \cdot 7\).
Checking,
\(\sqrt{2700}\)
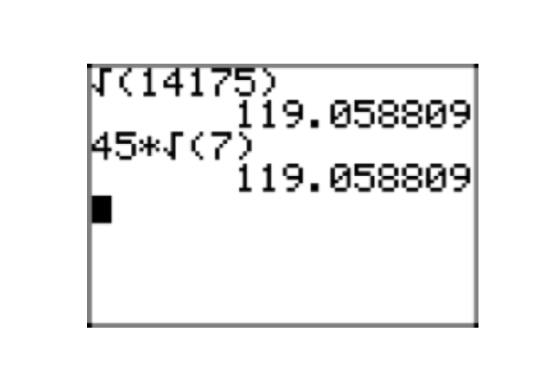
\(\sqrt{14175}\)
- Answer
-
Money! Anything that ends in 00, 25, 50, or 75 is divisible by 25. Indeed, \(14175 = 25 \cdot 567\). Further, 5+6+7 = 18, so 567 is divisible by 9; i.e., \(567 = 9 \cdot 63\). Continuing to primes,
\(14175 = 25 \cdot 567 = 5 \cdot 5 \cdot 9 \cdot 63 = 5 \cdot 5 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 7\).
Factor our a perfect square (exponents divisible by 2).
\(\sqrt{14175} = \sqrt{3^{4} \cdot 5^{2}} \cdot \sqrt{7} = 3^{2} \cdot 5\sqrt{7} = 45\sqrt{7}\)
Checking,
\(\sqrt{44000}\)
\(\sqrt{20250}\)
- Answer
-
Money! Anything that ends in 00, 25, 50, or 75 is divisible by 25. Indeed, \(20250 = 25 \cdot 810\). Continuing to primes,
\(20250 = 5 \cdot 5 \cdot 9 \cdot 9 \cdot 10 = 5 \cdot 5 \cdot 3 \cdot 3 \cdot 3 \cdot 3 \cdot 2 \cdot 5\).
Factor out a perfect square.
\(\sqrt{20250} = \sqrt{2 \cdot 3^{4} \cdot 5^{3}} = \sqrt{3^{4} \cdot 5^{2}} \cdot \sqrt{2 \cdot 5} = 3^{2} \cdot 5 \sqrt{2 \cdot 5}=45\sqrt{10}\)
Checking,
\(\sqrt{3564}\)
In Exercises 27-46, place each of the given radical expressions in simple radical form. Make no assumptions about the sign of the variables. Variables can either represent positive or negative numbers.
\(\sqrt{(6x−11)^4}\)
- Answer
-
\(\sqrt{(6x−11)^4} = \sqrt{((6x−11)^2)^2} = |(6x−11)^2|\)
However, \((6x − 11)^2\) is already nonnegative, so the absolute value bars are unnecessary. Hence,
\(\sqrt{(6x−11)^4} = (6x−11)^2\)
\(\sqrt{16h^8}\)
\(\sqrt{25f^2}\)
- Answer
-
\(\sqrt{25f^2} = \sqrt{25}\sqrt{f^2} = 5|f|\)
Because f can be any real number, we cannot remove the absolute value bars without more information.
\(\sqrt{25j^8}\)
\(\sqrt{16m^2}\)
- Answer
-
\(\sqrt{16m^2} = \sqrt{4^{2}m^2} = \sqrt{4^2}\sqrt{m^2} = 4|m|\)
Since the index on the radical is even and, after simplification, the variable is raised to an odd power, absolute value signs around the simplified variable are necessary.
\(\sqrt{25a^2}\)
\(\sqrt{(7x+5)^{12}}\)
- Answer
-
\(\sqrt{(7x+5)^{12}} = \sqrt{((7x+5)^6)^2} = |(7x+5)^6|\)
However, \((7x+5)^6\) is already nonnegative, so absolute value signs are unnecessary.
\(\sqrt{(7x+5)^{12}} = (7x+5)^6\)
\(\sqrt{9w^{10}}\)
\(\sqrt{25x^2−50x+25}\)
- Answer
-
\(\sqrt{25x^2−50x+25}=\sqrt{(5x−5)^2} =|5x−5|\)
Because x can be any real number, the absolute value signs around the simplified binomial are necessary.
\(\sqrt{49x^2−42x+9}\)
\(\sqrt{25x^2+90x+81}\)
- Answer
-
\(\sqrt{25x^2+90x+81} = \sqrt{(5x+9)^2} = |5x+9|\)
Because x can be any real number, the absolute value signs around the simplified binomial are necessary.
\(\sqrt{25f^{14}}\)
\(\sqrt{(3x+6)^{12}}\)
- Answer
-
\(\sqrt{(3x+6)^{12}} = \sqrt{((3x+6)^6)^2} = |(3x+6)^6|\)
However, the expression \((3x+6)^6\) is already nonnegative, so the absolute value bars are unnecessary.
\(\sqrt{(3x+6)^{12}} = (3x+6)^6\)
\(\sqrt{(9x−8)^{12}}\)
\(\sqrt{36x^2+36x+9}\)
- Answer
-
\(\sqrt{36x^2+36x+9} = \sqrt{(6x+3)^2} =|6x+3|\)
Because x can be any real number, the absolute value signs around the simplified binomial are necessary.
\(\sqrt{4e^2}\)
\(\sqrt{4p^{10}}\)
- Answer
-
\(\sqrt{4p^{10}} = \sqrt{4}\sqrt{(p^5)^2}=2|p^5|\)
Now, we can use the multiplicative property of absolute values and write
\(2|p^5| = 2|p^4||p| = 2p^{4}|p|\).
Since p can be any real number, absolute value signs around the simplified variable are necessary.
\(\sqrt{25x^{12}}\)
\(\sqrt{25q^6}\)
- Answer
-
\(\sqrt{25q^6} = \sqrt{25}\sqrt{(q^3)^2} = 5|q^3|\)
Now, we can use the multiplicative property of absolute values and write
\(5|q^3| = 5|q^2||q| = 5q^{2}|q|\).
Because q can be any real number, absolute value signs around the simplified variable are necessary.
\(\sqrt{16h^{12}}\)
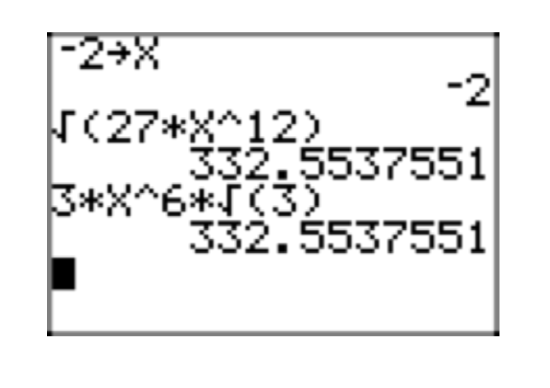
Given that x < 0, place the radical expression \(\sqrt{32x^6}\) in simple radical form. Check your solution on your calculator for x = −2.
- Answer
-
Factor out a perfect square.
\(\sqrt{32x^6} = \sqrt{16x^6}\sqrt{2} = \sqrt{16}\sqrt{x^6}\sqrt{2}=4|x^3|\sqrt{2}\)
However, \(|x^3| = |x^2||x| = x^2|x|\), since \(x^2 \ge 0\). Thus
\(\sqrt{32x^6} = 4x^{2}|x|\sqrt{2}\).
If x < 0, then |x| = −x and
\(\sqrt{32x^6} = 4x^{2}(−x)\sqrt{2} =−4x^{3}\sqrt{2}\).
Checking with x = −2.
Given that x < 0, place the radical expression \(\sqrt{54x^8}\) in simple radical form. Check your solution on your calculator for x = −2.
Given that x < 0, place the radical expression \(\sqrt{27x^{12}}\) in simple radical form. Check your solution on your calculator for x = −2.
Given that x < 0, place the radical expression \(\sqrt{44x^{10}}\) in simple radical form. Check your solution on your calculator for x = −2.
In Exercises 51-54, follow the lead of Example 17 in the narrative to simplify the given radical expression and check your result with your graphing calculator.
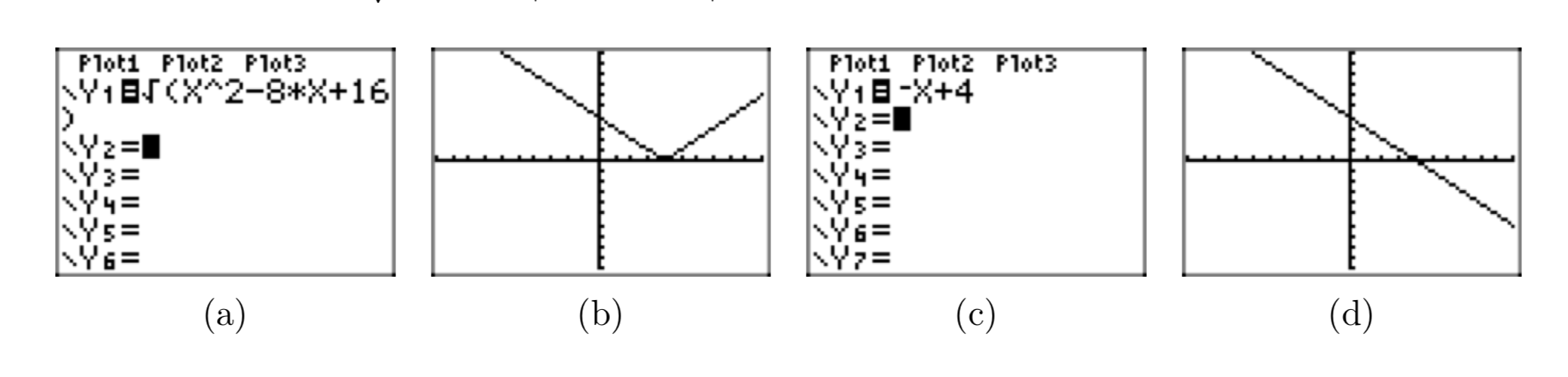
Given that x < 4, place the radical expression \(\sqrt{x^2−8x+16}\) in simple radical form. Use a graphing calculator to show that the graphs of the original expression and your simple radical form agree for all values of x such that x < 4.
- Answer
-
Factor the perfect square trinomial.
\(\sqrt{x^2−8x+16} = \sqrt{(x−4)^2} =|x−4|\)
If x < 4, or equivalently, if x−4 < 0, then |x−4| = −(x−4). Thus,
\(\sqrt{x^2−8x+16} =−x+4\).
In (b), we've drawn the graph of \(y = \sqrt{x^2−8x+16}\). In (d), we've drawn the graph of y = −x+4. Note that the graphs in (b) and (d) agree when x < 4, leading credence to the fact that \(\sqrt{x^2−8x+16} =−x+4\) when x < 4.
Given that \(x \ge −2\), place the radical expression \(\sqrt{x^2+4x+4}\) in simple radical form. Use a graphing calculator to show that the graphs of the original expression and your simple radical form agree for all values of x such that \(x \ge −2\).
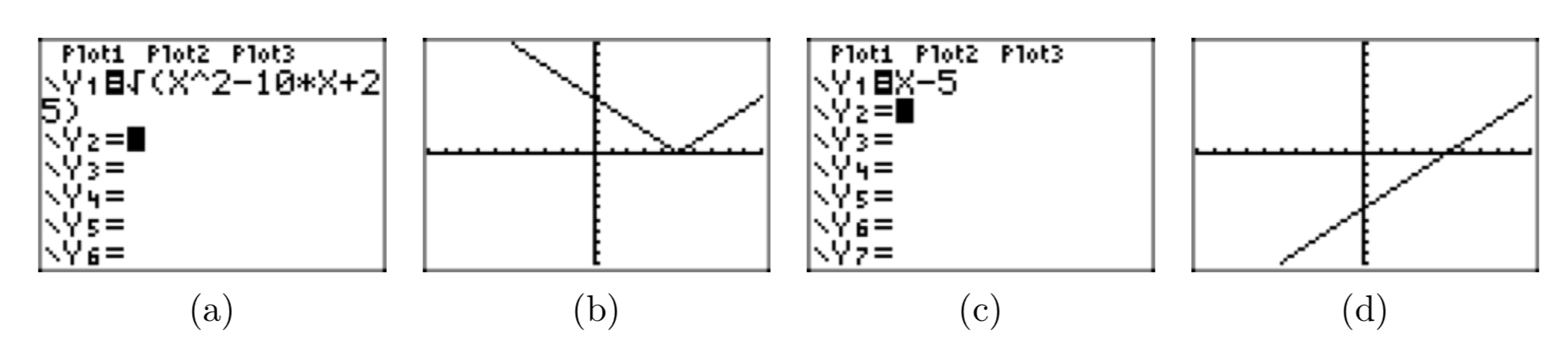
Given that \(x \ge 5\), place the radical expression \(\sqrt{x^2−10x+25}\) in simple radical form. Use a graphing calculator to show that the graphs of the original expression and your simple radical form agree for all values of x such that \(x \ge 5\).
- Answer
-
Factor the perfect square trinomial.
\(\sqrt{x^2−10x+25} = \sqrt{(x−5)^2} =|x−5|\)
If \(x \ge 5\), or equivalently, if \(x−5 \ge 0\), then |x−5| = x−5. Thus,
\(\sqrt{x^2−8x+16} =x−5\).
In (b), we've drawn the graph of \(y = \sqrt{x^2−10x+25}\). In (d), we've drawn the graph of y = x−5. Note that the graphs in (b) and (d) agree when \(x \ge 5\), leading credence to the fact that \(\sqrt{x^2−10x+25} = x−5\) when \(x \ge 5\).
Given that x < −1, place the radical expression \(\sqrt{x^2+2x+1}\) in simple radical form. Use a graphing calculator to show that the graphs of the original expression and your simple radical form agree for all values of x such that x < −1.
In Exercises 55-72, place each radical expression in simple radical form. Assume that all variables represent positive numbers.
\(\sqrt{9d^{13}}\)
- Answer
-
\(\sqrt{9d^{13}} = \sqrt{9}\sqrt{d^{12}}\sqrt{d}=3d^6\sqrt{d}\)
\(\sqrt{4k^2}\)
\(\sqrt{25x^2+40x+16}\)
- Answer
-
\(\sqrt{25x^2+40x+16} = \sqrt{(5x+4)^2} = 5x+4\)
\(\sqrt{9x^2−30x+25}\)
\(\sqrt{4j^{11}}\)
- Answer
-
\(\sqrt{4j^{11}} = \sqrt{4}\sqrt{j^{10}}\sqrt{j}=3j^5\sqrt{j}\)
\(\sqrt{16j^6}\)
\(\sqrt{25m^2}\)
- Answer
-
\(\sqrt{25m^2} = \sqrt{25}\sqrt{m^2} = 5m\)
\(\sqrt{9e^9}\)
\(\sqrt{4c^5}\)
- Answer
-
\(\sqrt{4c^5} = \sqrt{4c^4}\sqrt{c} = 2c^{2}\sqrt{c}\)
\(\sqrt{25z^2}\)
\(\sqrt{25h^{10}}\)
- Answer
-
\(\sqrt{25h^{10}} = \sqrt{25}\sqrt{h^{10}} = 5h^5\)
\(\sqrt{25b^2}\)
\(\sqrt{9s^7}\)
- Answer
-
\(\sqrt{9s^7} = \sqrt{9s^6}\sqrt{s} = 3s^{3}\sqrt{s}\)
\(\sqrt{9e^7}\)
\(\sqrt{4p^8}\)
- Answer
-
\(\sqrt{4p^8} = \sqrt{4}\sqrt{p^8} = 2\sqrt{p^4}\)
\(\sqrt{9d^{15}}\)
\(\sqrt{9q^{10}}\)
- Answer
-
\(\sqrt{9q^{10}} = \sqrt{9}\sqrt{q^{10}} = 3\sqrt{q^5}\)
\(\sqrt{4w^7}\)
In Exercises 73-80, place each given radical expression in simple radical form. Assume that all variables represent positive numbers.
\(\sqrt{2f^5}\sqrt{8f^3}\)
- Answer
-
\(\sqrt{2f^5}\sqrt{8f^3} =\sqrt{2 \cdot 8 \cdot f^5 \cdot f^3} = \sqrt{16f^8} = \sqrt{16}\sqrt{(f^4)^2} =4f^4\)
\(\sqrt{3s^3}\sqrt{243s^3}\)
\(\sqrt{2k^7}\sqrt{32k^3}\)
- Answer
-
\(\sqrt{2k^7}\sqrt{32k^3} = \sqrt{2 \cdot 32 \cdot k^7 \cdot k^3} = \sqrt{64k^{10}} = \sqrt{64}\sqrt{(k^5)^2}=8k^5\)
\(\sqrt{2n^9}\sqrt{8n^3}\)
\(\sqrt{2e^9}\sqrt{8e^3}\)
- Answer
-
\(\sqrt{2e^9}\sqrt{8e^3} = \sqrt{2 \cdot 8 \cdot e^9 \cdot e^3} = \sqrt{16e^{12}} = \sqrt{16}\sqrt{(e^6)^2}=4e^6\)
\(\sqrt{5n^9}\sqrt{125n^3}\)
\(\sqrt{3z^5}\sqrt{27z^3}\)
- Answer
-
\(\sqrt{3z^5}\sqrt{27z^3} = \sqrt{3 \cdot 27 \cdot z^5 \cdot z^3} = \sqrt{81z^8} = \sqrt{81}\sqrt{(z^4)^2}=9z^4\)
\(\sqrt{3t^7}\sqrt{27t^3}\)