11.3E: Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Practice Makes Perfect
In the following exercises, graph each equation by using properties.
- y=−x2+4x−3
- y=−x2+8x−15
- y=6x2+2x−1
- y=8x2−10x+3
- Answer
-
1.
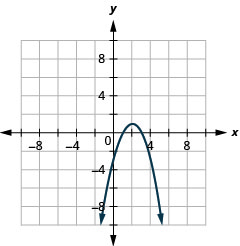
Figure 11.2.83 3.
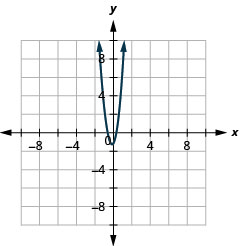
Figure 11.2.84
In the following exercises,
- Write the equation in standard form and
- Use properties of the standard form to graph the equation.
- y=−x2+2x−4
- y=2x2+4x+6
- y=−2x2−4x−5
- y=3x2−12x+7
- Answer
-
1.
- y=−(x−1)2−3
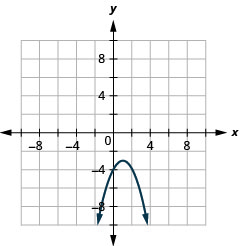
Figure 11.2.85 3.
- y=−2(x+1)2−3
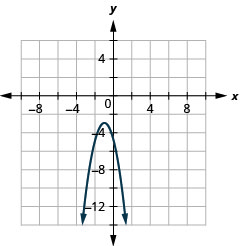
Figure 11.2.86
In the following exercises, graph each equation by using properties.
- x=−2y2
- x=3y2
- x=4y2
- x=−4y2
- x=−y2−2y+3
- x=−y2−4y+5
- x=y2+6y+8
- x=y2−4y−12
- x=(y−2)2+3
- x=(y−1)2+4
- x=−(y−1)2+2
- x=−(y−4)2+3
- x=(y+2)2+1
- x=(y+1)2+2
- x=−(y+3)2+2
- x=−(y+4)2+3
- x=−3(y−2)2+3
- x=−2(y−1)2+2
- x=4(y+1)2−4
- x=2(y+4)2−2
- Answer
-
1.
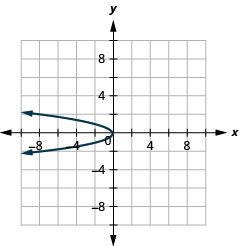
Figure 11.2.87 3.
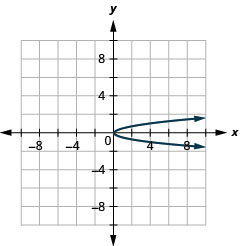
Figure 11.2.88 5.
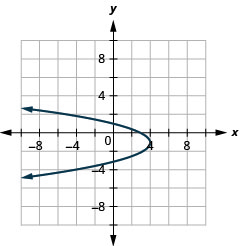
Figure 11.2.89 7.
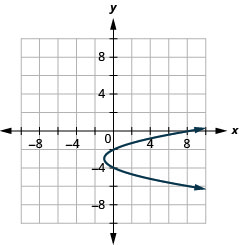
Figure 11.2.90 9.
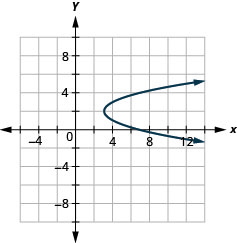
Figure 11.2.91 11.
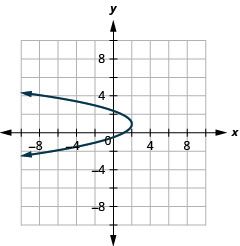
Figure 11.2.92 13.
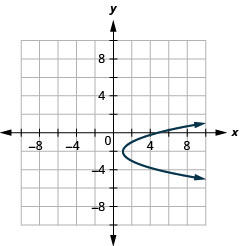
Figure 11.2.93 15.
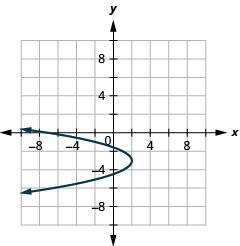
Figure 11.2.94 17.
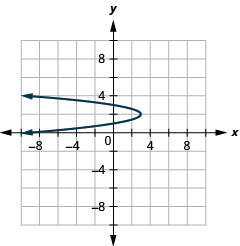
Figure 11.2.95 19.
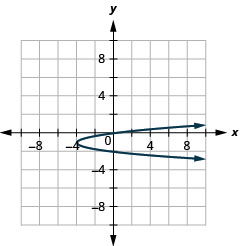
Figure 11.2.96
In the following exercises,
- Write the equation in standard form and
- Use properties of the standard form to graph the equation.
- x=y2+4y−5
- x=y2+2y−3
- x=−2y2−12y−16
- x=−3y2−6y−5
- Answer
-
1.
- x=(y+2)2−9
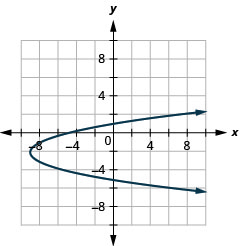
Figure 11.2.97 3.
- x=−2(y+3)2+2
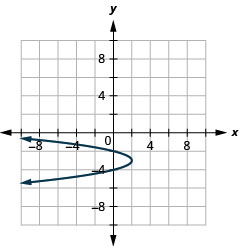
Figure 11.2.98
In the following exercises, match each graph to one of the following equations:
- x2+y2=64
- x2+y2=49
- (x+5)2+(y+2)2=4
- (x−2)2+(y−3)2=9
- y=−x2+8x−15
- y=6x2+2x−1
1.
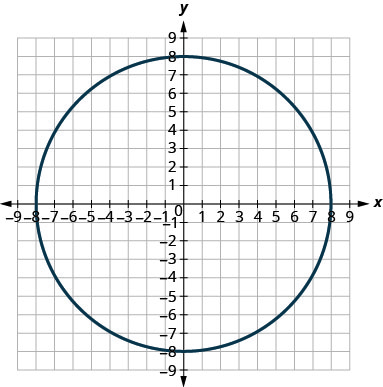
2.
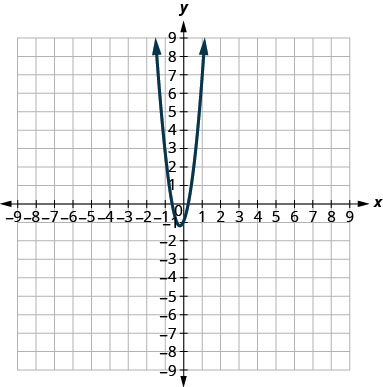
3.
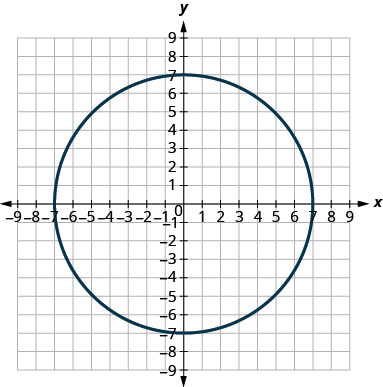
4.
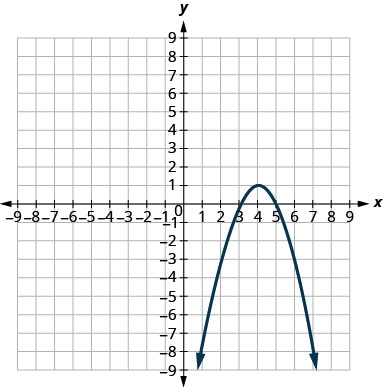
5.
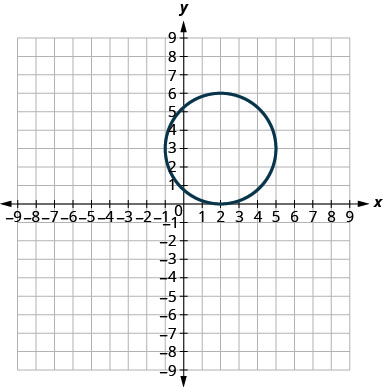
6.
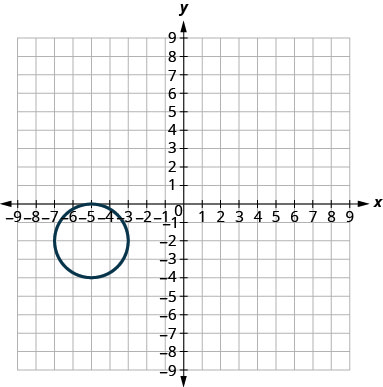
- Answer
-
1. a
3. b
5. d
Write the equation in standard form of the parabolic arch formed in the foundation of the bridge shown. Use the lower left side of the bridge as the origin (0,0).
1.
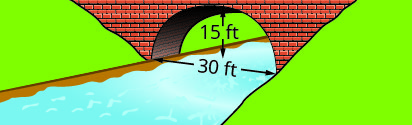
2.
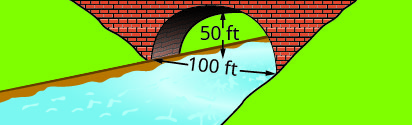
3.
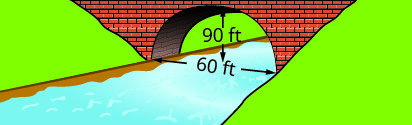
4.
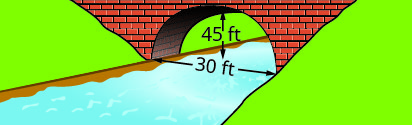
- Answer
-
1. y=−115(x−15)2+15
3. y=−110(x−30)2+90
- In your own words, define a parabola.
- Is the parabola y=x2 a function? Is the parabola x=y2 a function? Explain why or why not.
- Write the equation of a parabola that opens up or down in standard form and the equation of a parabola that opens left or right in standard form. Provide a sketch of the parabola for each one, label the vertex and axis of symmetry.
- Explain in your own words, how you can tell from its equation whether a parabola opens up, down, left or right.
- Answer
-
1. Answers may vary
3. Answers may vary
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. After reviewing this checklist, what will you do to become confident for all objectives?


