11.4: Ellipses
- Page ID
- 5189
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Graph an ellipse with center at the origin
- Find the equation of an ellipse with center at the origin
- Graph an ellipse with center not at the origin
- Solve application with ellipses
Before you get started, take this readiness quiz.
- Graph \(y=(x-1)^{2}-2\) using transformations.
If you missed this problem, review Example 9.57. - Complete the square: \(x^{2}-8 x=8\).
If you missed this problem, review Example 9.12. - Write in standard form. \(y=2 x^{2}-12 x+14\)
If you missed this problem, review Example 9.59.
Graph an Ellipse with Center at the Origin
The next conic section we will look at is an ellipse. We define an ellipse as all points in a plane where the sum of the distances from two fixed points is constant. Each of the given points is called a focus of the ellipse.
An ellipse is all points in a plane where the sum of the distances from two fixed points is constant. Each of the fixed points is called a focus of the ellipse.
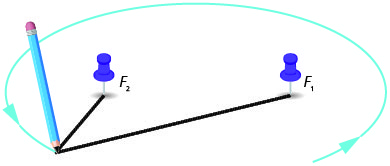
We can draw an ellipse by taking some fixed length of flexible string and attaching the ends to two thumbtacks. We use a pen to pull the string taut and rotate it around the two thumbtacks. The figure that results is an ellipse.
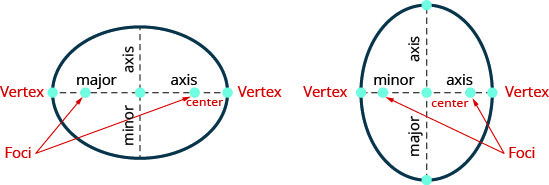
A line drawn through the foci intersect the ellipse in two points. Each point is called a vertex of the ellipse. The segment connecting the vertices is called the major axis. The midpoint of the segment is called the center of the ellipse. A segment perpendicular to the major axis that passes through the center and intersects the ellipse in two points is called the minor axis.
We mentioned earlier that our goal is to connect the geometry of a conic with algebra. Placing the ellipse on a rectangular coordinate system gives us that opportunity. In the figure, we placed the ellipse so the foci \(((−c,0),(c,0))\) are on the \(x\)-axis and the center is the origin.
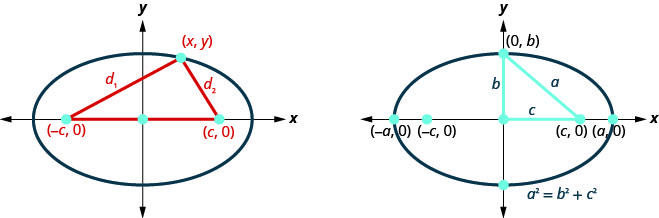
The definition states the sum of the distance from the foci to a point \((x,y)\) is constant. So \(d_{1}+d_{2}\) is a constant that we will call \(2a\) so, \(d_{1}+d_{2}=2 a\). We will use the distance formula to lead us to an algebraic formula for an ellipse.
\(d_{1} \quad+\quad \quad d_{2} \quad=\quad 2 a\)
Use the distance formula to find \(d_{1},d_{2}\).
\(\sqrt{(x-(-c))^{2}+(y-0)^{2}}+\sqrt{(x-c)^{2}+(y-0)^{2}}=2 a\)
After eliminating radicals and simplifying,we get:
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}-c^{2}}=1\)
To simplify the equation of the ellipse, we let \(a^{2}−c^{2}=b^{2}\).So, the equation of an ellipse centered at the origin in standard form is:
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
To graph the ellipse, it will be helpful to know the intercepts. We will find the \(x\)-intercepts and \(y\)-intercepts using the formula.
\(y\)-intercepts
Let \(x=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}+\frac{y^{2}}{a^{2}} &=1 \\ \frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=b^{2} \\ y &=\pm b \end{aligned}\)
The \(y\)-intercepts are \((0,b)\) and \((0, -b)\).
\(x\)-intercepts
Let \(y=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}+\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)
The \(x\)-intercepts are \((a,0)\) and \((-a,0)\).
Standard Form of the Equation an Ellipse with Center \((0,0)\)
The standard form of the equation of an ellipse with center \((0,0)\), is
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
The \(x\)-intercepts are \((a,0)\) and \((−a,0)\).
The \(y\)-intercepts are \((0,b)\) and \((0,−b)\).
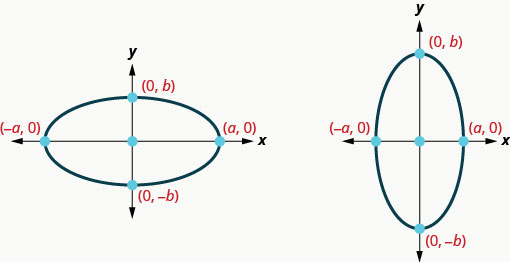
Notice that when the major axis is horizontal, the value of \(a\) will be greater than the value of \(b\) and when the major axis is vertical, the value of \(b\) will be greater than the value of \(a\). We will use this information to graph an ellipse that is centered at the origin.
Ellipse with Center \((0,0)\)
| \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) | \(a>b\) | \(b>a\) |
|---|---|---|
| Major axis | on the \(x\)-axis. | on the \(y\)-axis |
| \(x\)-intercepts | \((-a, 0),(a, 0)\) | |
| \(y\)-intercepts | \((0,-b),(0, b)\) |
Graph: \(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\).
Solution:
| Step 1. Write the equation in standard form. | It is in standard form. | \(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) |
| Step 2. Determine whether the major axis is horizontal or vertical. | Since \(9>4\) and \(9\) is in the \(y^{2}\) term, the major axis is vertical. | Major axis is vertical. |
| Step 3. Find the endpoints of the major axis. |
The endpoints will be the \(y\)-intercepts. Since \(b^{2}=9\), then \(b=\pm 3\). The endpoints of the major axis are \((0,3),(0,-3)\). |
The endpoints of the major axis are \((0,3),(0,-3)\). |
| Step 4. Find the endpoints of the minor axis. | The endpoints will be the \(x\)-intercepts.
Since \(a^{2}=4\), then \(a=\pm 2\). The endpoints of the major axis are \((2,0),(-2,0)\). |
The endpoints of the major axis are \((2,0),(-2,0)\). |
| Step 5. Sketch the ellipse. | .png?revision=1) |
Graph: \(\frac{x^{2}}{4}+\frac{y^{2}}{16}=1\).
- Answer
-
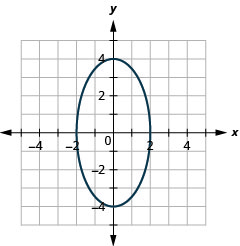
Figure 11.3.7
Graph: \(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\).
- Answer
-
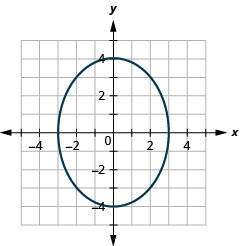
Figure 11.3.8
We summarize the steps for reference.
HOW TO GRAPH AN ELLIPSE WITH CENTER \((0,0)\).
- Write the equation in standard form.
- Determine whether the major axis is horizontal or vertical.
- Find the endpoints of the major axis.
- Find the endpoints of the minor axis
- Sketch the ellipse.
Sometimes our equation will first need to be put in standard form.
Graph \(x^{2}+4 y^{2}=16\).
Solution:
| We recognize this as the equation of an ellipse since both the \(x\) and \(y\) terms are squared and have different coefficients. |
\(x^{2}+4 y^{2}=16\) |
| To get the equation in standard form, divide both sides by \(16\) so that the equation is equal to \(1\). |
\(\frac{x^{2}}{16}+\frac{4 y^{2}}{16}=\frac{16}{16}\) |
| Simplify. | \(\frac{x^{2}}{16}+\frac{y^{2}}{4}=1\) |
| The equation is in standard form. The ellipse is centered at the origin. |
The center is \((0,0)\). |
| Since \(16>4\) and \(16\) is in the \(x^{2}\) term, the major axis is horizontal. |
|
| \(a^{2}=16, a=\pm 4\) \(b^{2}=4, \quad b=\pm 2\) |
The vertices are \((4,0),(−4,0)\). The endpoints of the minor axis are \((0,2),(0,−2)\). |
| Sketch the parabola. | 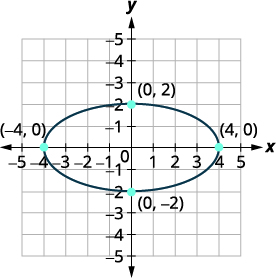 |
Graph \(9 x^{2}+16 y^{2}=144\).
- Answer
-
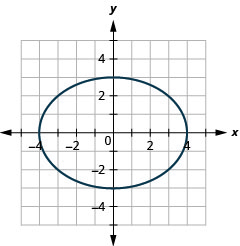
Figure 11.3.10
Graph \(16 x^{2}+25 y^{2}=400\).
- Answer
-
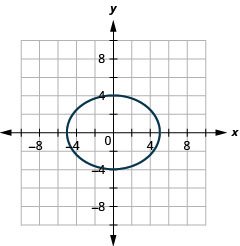
Figure 11.3.11
Find the Equation of an Ellipse with Center at the Origin
If we are given the graph of an ellipse, we can find the equation of the ellipse.
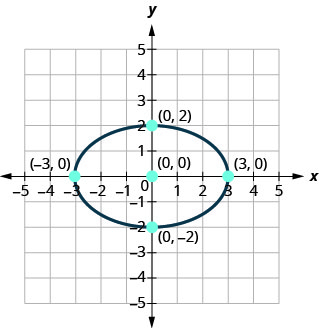
Find the equation of the ellipse shown.
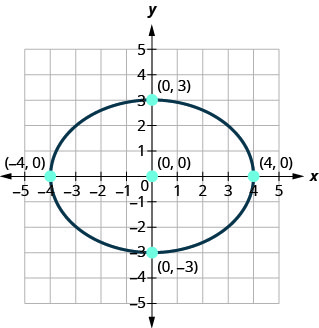
Solution:
We recognize this as an ellipse that is centered at the origin.
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
Since the major axis is horizontal and the distance from the center to the vertex is \(4\), we know \(a=4\) and so \(a^{2}=16\).
\(\frac{x^{2}}{16}+\frac{y^{2}}{b^{2}}=1\)
The minor axis is vertical and the distance from the center to the ellipse is \(3\), we know \(b=3\) and so \(b^{2}=9\).
\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)
Find the equation of the ellipse shown.
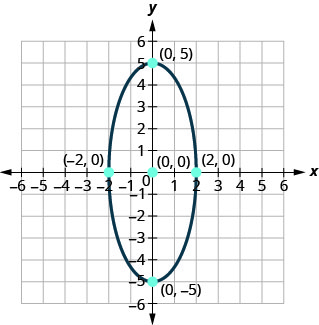
- Answer
-
\(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
Find the equation of the ellipse shown.
- Answer
-
\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\)
Graph an Ellipse with Center Not at the Origin
The ellipses we have looked at so far have all been centered at the origin. We will now look at ellipses whose center is \((h,k)\).
The equation is \(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) and when \(a>b\), the major axis is horizontal so the distance from the center to the vertex is \(a\). When \(b>a\), the major axis is vertical so the distance from the center to the vertex is \(b\).
Standard Form of the Equation an Ellipse with Center \((h,k)\)
The standard form of the equation of an ellipse with center \((h,k)\), is
\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)
When \(a>b\), the major axis is horizontal so the distance from the center to the vertex is \(a\).
When \(b>a\), the major axis is vertical so the distance from the center to the vertex is \(b\).
Graph: \(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\).
Solution:
| The equation is in standard form, \(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). | \(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\) |
| The ellipse is centered at \((h,k)\). | The center is \((3,1)\). |
| Since \(9>4\) and \(9\) is in the \(x^{2}\) term, the major axis is horizontal. | |
| \(a^{2}=9, a=\pm 3\) \(b^{2}=4, b=\pm 2\) |
The distance from the center to the vertices is \(3\). The distance from the center to the endpoints of the minor axis is \(2\). |
| Sketch the ellipse. | 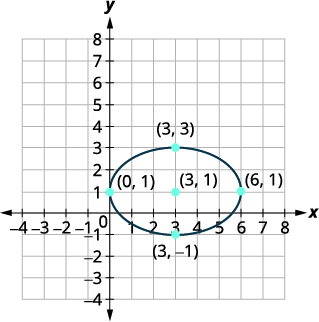 |
Graph: \(\frac{(x+3)^{2}}{4}+\frac{(y-5)^{2}}{16}=1\).
- Answer
-
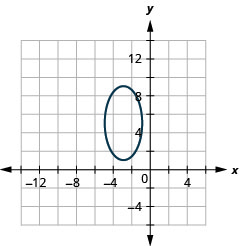
Figure 11.3.16
Graph: \(\frac{(x-1)^{2}}{25}+\frac{(y+3)^{2}}{16}=1\).
- Answer
-
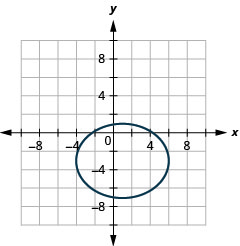
Figure 11.3.17
If we look at the equations of \(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\) and \(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\), we see that they are both ellipses with \(a=3\) and \(b=2\). So they will have the same size and shape. They are different in that they do not have the same center.
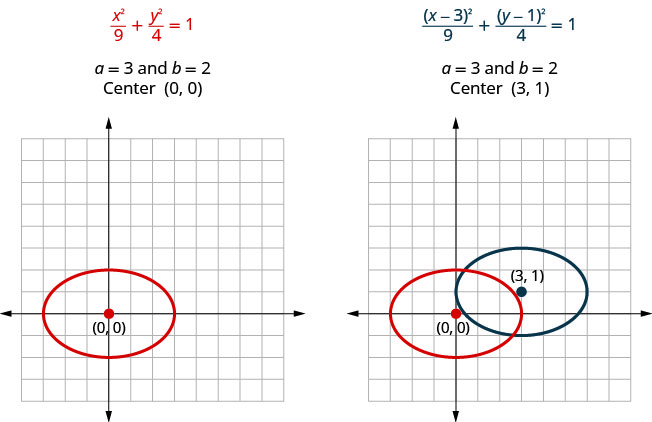
Notice in the graph above that we could have graphed \(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\) by translations. We moved the original ellipse to the right \(3\) units and then up \(1\) unit.
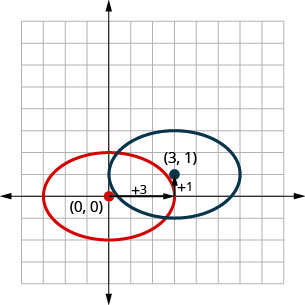
In the next example we will use the translation method to graph the ellipse.
Graph \(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\) by translation.
Solution:
This ellipse will have the same size and shape as \(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) whose center is \((0,0)\). We graph this ellipse first.
| The center is \((0,0)\). | Center \((0,0)\) |
| Since \(16>9\), the major axis is horizontal. | |
| \(a^{2}=16, a=\pm 4\) \(b^{2}=9, \quad b=\pm 3\) |
The vertices are \((4,0),(−4,0)\). The endpoints of the minor axis are \((0,3),(0,−3)\). |
| Sketch the ellipse. | 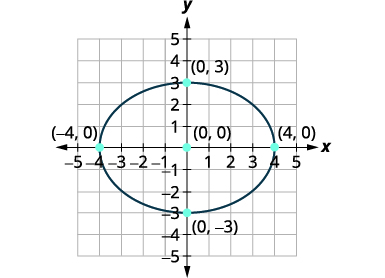 |
| The original equation is in standard form, \(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). | \(\frac{(x-(-4))^{2}}{16}+\frac{(y-6)^{2}}{9}=1\) |
| The ellipse is centered at \((h,k)\). | The center is \((-4,6)\). |
| We translate the graph of \(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) four units to the left and then up \(6\) units. Verify that the center is \((−4,6)\). The new ellipse is the ellipse whose equation is \(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\). |
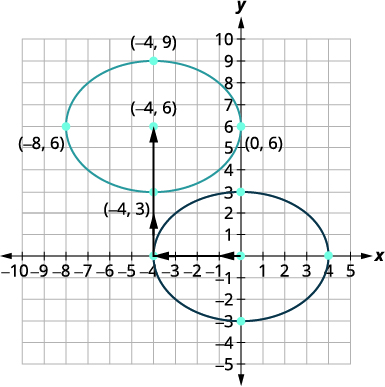 |
Graph \(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{4}=1\) by translation.
- Answer
-
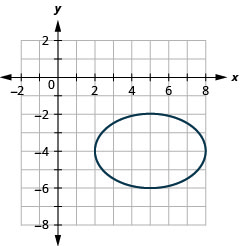
Figure 11.3.22
Graph \(\frac{(x+6)^{2}}{16}+\frac{(y+2)^{2}}{25}=1\) by translation.
- Answer
-
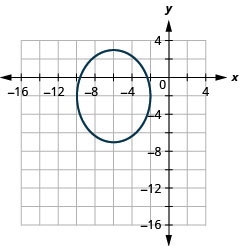
Figure 11.3.23
When an equation has both an \(x^{2}\) and a \(y^{2}\) with different coefficients, we verify that it is an ellipsis by putting it in standard form. We will then be able to graph the equation.
Write the equation \(x^{2}+4 y^{2}-4 x+24 y+24=0\) in standard form and graph.
Solution:
We put the equation in standard form by completing the squares in both \(x\) and \(y\).
| \(x^{2}+4 y^{2}-4 x+24 y+24=0\) | |
| Rewrite grouping the \(x\) terms and \(y\) terms. | 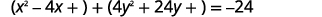 |
| Make the coefficients of \(x^{2}\) and \(y^{2}\) equal \(1\). | 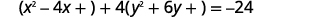 |
| Complete the squares. | 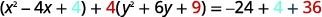 |
| Write as binomial squares. | 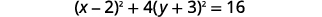 |
| Divide both sides by \(16\) to get \(1\) on the right. | 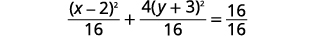 |
| Simplify. | 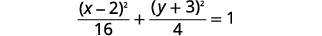 |
| The equation is in standard form, \(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) | 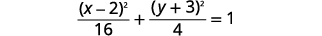 |
| The ellipse is centered at \((h,k)\). | The center is \((2,-3)\). |
|
Since \(16>4\) and \(16\) is in the \(x^{2}\) term, the major axis is horizontal. \(a^{2}=16, a=\pm 4\) |
The distance from the center to the vertices is \(4\). The distance from the center to the endpoints of the minor axis is \(2\). |
| Sketch the ellipse. | 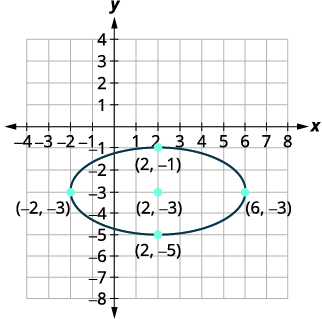 |
- Write the equation \(6 x^{2}+4 y^{2}+12 x-32 y+34=0\) in standard form and
- Graph.
- Answer
-
- \(\frac{(x+1)^{2}}{6}+\frac{(y-4)^{2}}{9}=1\)
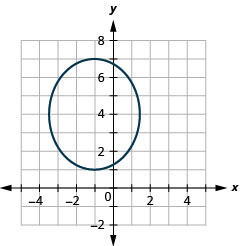
Figure 11.3.32
- Write the equation \(4 x^{2}+y^{2}-16 x-6 y+9=0\) in standard form and
- Graph.
- Answer
-
- \(\frac{(x-2)^{2}}{4}+\frac{(y-3)^{2}}{16}=1\)
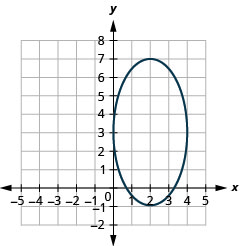
Figure 11.3.33
Solve Application with Ellipses
The orbits of the planets around the sun follow elliptical paths.
Pluto (a dwarf planet) moves in an elliptical orbit around the Sun. The closest Pluto gets to the Sun is approximately \(30\) astronomical units (AU) and the furthest is approximately \(50\) AU. The Sun is one of the foci of the elliptical orbit. Letting the ellipse center at the origin and labeling the axes in AU, the orbit will look like the figure below. Use the graph to write an equation for the elliptical orbit of Pluto.
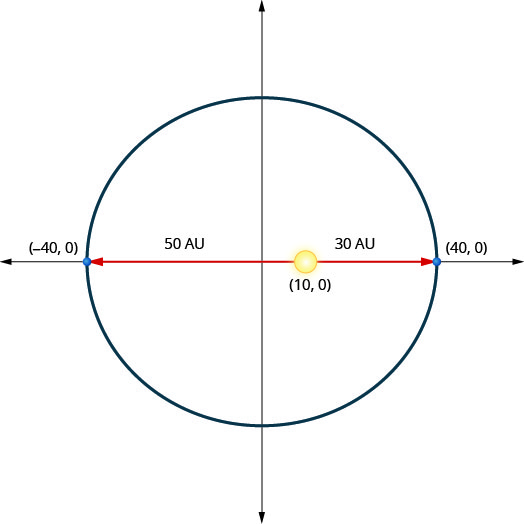
Solution:
We recognize this as an ellipse that is centered at the origin.
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
Since the major axis is horizontal and the distance from the center to the vertex is \(40\), we know \(a=40\) and so \(a^{2}=1600\).
\(\frac{x^{2}}{1600}+\frac{y^{2}}{b^{2}}=1\)
The minor axis is vertical but the end points aren’t given.To find \(b\) we will use the location of the Sun. Since the Sun is a focus of the ellipse at the point \((10,0)\),we know \(c=10\). Use this to solve for \(b^{2}\).
\(b^{2}=a^{2}-c^{2}\)
\(b^{2}=40^{2}-10^{2}\)
\(b^{2}=1600-100\)
\(b^{2}=1500\)
Substitute \(a^{2}\) and \(b^{2}\) into the standard form of the ellipse.
\(\frac{x^{2}}{1600}+\frac{y^{2}}{1500}=1\)
A planet moves in an elliptical orbit around its sun. The closest the planet gets to the sun is approximately \(20\) AU and the furthest is approximately \(30\) AU. The sun is one of the foci of the elliptical orbit. Letting the ellipse center at the origin and labeling the axes in AU, the orbit will look like the figure below. Use the graph to write an equation for the elliptical orbit of the planet.
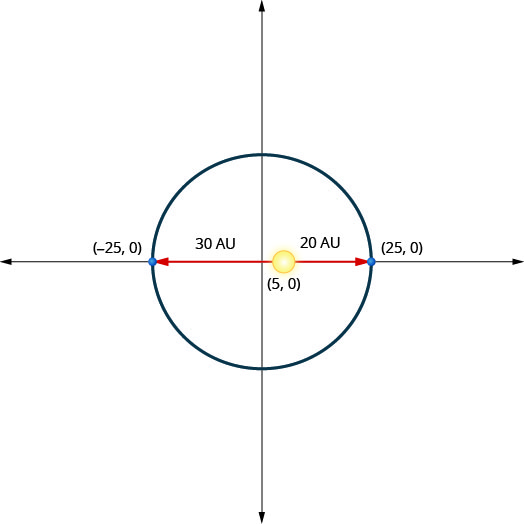
- Answer
-
\(\frac{x^{2}}{625}+\frac{y^{2}}{600}=1\)
A planet moves in an elliptical orbit around its sun. The closest the planet gets to the sun is approximately \(20\) AU and the furthest is approximately \(50\) AU. The sun is one of the foci of the elliptical orbit. Letting the ellipse center at the origin and labeling the axes in AU, the orbit will look like the figure below. Use the graph to write an equation for the elliptical orbit of the planet.
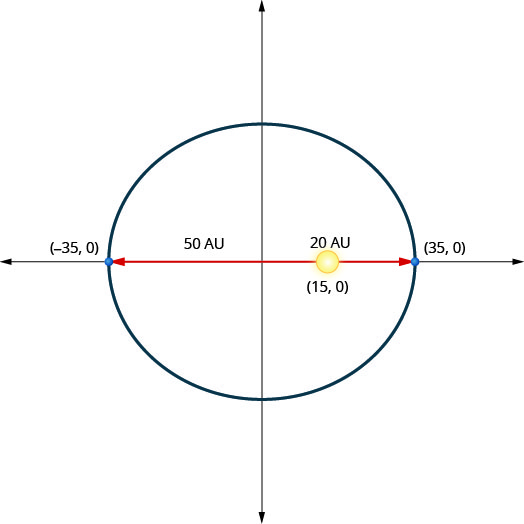
- Answer
-
\(\frac{x^{2}}{1225}+\frac{y^{2}}{1000}=1\)
Access these online resources for additional instructions and practice with ellipses.
- Conic Sections: Graphing Ellipses Part 1
- Conic Sections: Graphing Ellipses Part 2
- Equation for Ellipse From Graph
Key Concepts
- Ellipse: An ellipse is all points in a plane where the sum of the distances from two fixed points is constant. Each of the fixed points is called a focus of the ellipse.
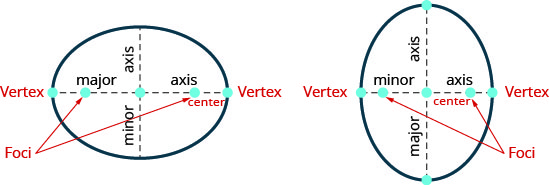
Figure 11.3.37
- If we draw a line through the foci intersects the ellipse in two points—each is called a vertex of the ellipse.
The segment connecting the vertices is called the major axis.
The midpoint of the segment is called the center of the ellipse.
A segment perpendicular to the major axis that passes through the center and intersects the ellipse in two points is called the minor axis. - Standard Form of the Equation an Ellipse with Center \((0,0)\): The standard form of the equation of an ellipse with center \((0,0)\), is
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
The \(x\)-intercepts are \((a,0)\) and \((−a,0)\).
The \(y\)-intercepts are \((0,b)\) and \((0,−b)\). - How to an Ellipse with Center \((0,0)\)
- Write the equation in standard form.
- Determine whether the major axis is horizontal or vertical.
- Find the endpoints of the major axis.
- Find the endpoints of the minor axis
- Sketch the ellipse.
- Standard Form of the Equation an Ellipse with Center \((h,k)\): The standard form of the equation of an ellipse with center \((h,k)\), is
\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)
When \(a>b\), the major axis is horizontal so the distance from the center to the vertex is \(a\).
When \(b>a\), the major axis is vertical so the distance from the center to the vertex is \(b\).
Glossary
- ellipse
- An ellipse is all points in a plane where the sum of the distances from two fixed points is constant.


