11.5: Hyperbolas
- Page ID
- 5191
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)By the end of this section, you will be able to:
- Graph a hyperbola with center at \((0,0)\)
- Graph a hyperbola with center at \((h,k)\)
- Identify conic sections by their equations
Before you get started, take this readiness quiz.
- Solve: \(x^{2}=12\).
If you missed this problem, review Example 9.1. - Expand: \((x−4)^{2}\).
If you missed this problem, review Example 5.32. - Graph \(y=-\frac{2}{3} x\).
If you missed this problem, review Example 3.4.
Graph a Hyperbola with Center at \((0,0)\)
The last conic section we will look at is called a hyperbola. We will see that the equation of a hyperbola looks the same as the equation of an ellipse, except it is a difference rather than a sum. While the equations of an ellipse and a hyperbola are very similar, their graphs are very different.
We define a hyperbola as all points in a plane where the difference of their distances from two fixed points is constant. Each of the fixed points is called a focus of the hyperbola.
A hyperbola is all points in a plane where the difference of their distances from two fixed points is constant. Each of the fixed points is called a focus of the hyperbola.
The line through the foci, is called the transverse axis. The two points where the transverse axis intersects the hyperbola are each a vertex of the hyperbola. The midpoint of the segment joining the foci is called the center of the hyperbola. The line perpendicular to the transverse axis that passes through the center is called the conjugate axis. Each piece of the graph is called a branch of the hyperbola.
Again our goal is to connect the geometry of a conic with algebra. Placing the hyperbola on a rectangular coordinate system gives us that opportunity. In the figure, we placed the hyperbola so the foci \(((−c,0),(c,0))\) are on the \(x\)-axis and the center is the origin.
The definition states the difference of the distance from the foci to a point \((x,y)\) is constant. So \(|d_{1}−d_{2}|\) is a constant that we will call \(2a\) so \(|d_{1}-d_{2} |=2 a\). We will use the distance formula to lead us to an algebraic formula for an ellipse.
\(\left|d_{1} - d_{2}\right| =2 a\)
Use the distance formula to find \(d_{1}, d_{2}\)
\(\left|\sqrt{(x-(-c))^{2}+(y-0)^{2}}-\sqrt{(x-c)^{2}+(y-0)^{2}}\right|=2 a\)
Eliminate the radicals. To simplify the equation of the ellipse, we let \(c^{2}-a^{2}=b^{2}\).
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{c^{2}-a^{2}}=1\)
So, the equation of a hyperbola centered at the origin in standard form is:
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\)
To graph the hyperbola, it will be helpful to know about the intercepts. We will find the \(x\)-intercepts and \(y\)-intercepts using the formula.
\(x\)-intercepts
Let \(y=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}-\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)
The \(x\)-intercepts are \((a,0)\) and \((−a,0)\).
\(y\)-intercepts
Let \(x=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}-\frac{y^{2}}{b^{2}} &=1 \\-\frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=-b^{2} \\ y &=\pm \sqrt{-b^{2}} \end{aligned}\)
There are no \(y\)-intercepts.
The \(a, b\) values in the equation also help us find the asymptotes of the hyperbola. The asymptotes are intersecting straight lines that the branches of the graph approach but never intersect as the \(x, y\) values get larger and larger.
To find the asymptotes, we sketch a rectangle whose sides intersect the x-axis at the vertices \((−a,0),(a,0)\), and intersect the \(y\)-axis at \((0,−b), (0,b)\). The lines containing the diagonals of this rectangle are the asymptotes of the hyperbola. The rectangle and asymptotes are not part of the hyperbola, but they help us graph the hyperbola.
The asymptotes pass through the origin and we can evaluate their slope using the rectangle we sketched. They have equations \(y=\frac{b}{a} x\) and \(y=-\frac{b}{a} x\).
There are two equations for hyperbolas, depending whether the transverse axis is vertical or horizontal. We can tell whether the transverse axis is horizontal by looking at the equation. When the equation is in standard form, if the \(x^{2}\)-term is positive, the transverse axis is horizontal. When the equation is in standard form, if the \(y^{2}\)-term is positive, the transverse axis is vertical.
The second equations could be derived similarly to what we have done. We will summarize the results here.
Standard Form of the Equation a Hyperbola with Center \((0,0)\)
The standard form of the equation of a hyperbola with center \((0,0)\), is
\(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \quad\) or \(\quad \frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\)
Notice that, unlike the equation of an ellipse, the denominator of \(x^{2}\) is not always \(a^{2}\) and the denominator of \(y^{2}\) is not always \(b^{2}\).
Notice that when the \(x^{2}\)-term is positive, the transverse axis is on the \(x\)-axis. When the \(y^{2}\)-term is positive, the transverse axis is on the \(y\)-axis.
Standard Forms of the Equation a Hyperbola with Center \((0,0)\)
| \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) | \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\) | |
|---|---|---|
| Orientation | Transverse axis on the \(x\)-axis. Opens left and right |
Transverse axis on the \(y\)-axis. Opens up and down |
| Vertices | \((-a, 0),(a, 0)\) | \((0,-a),(0, a)\) |
| \(x\)-intercepts | \((-a, 0),(a, 0)\) | none |
| \(y\)-intercepts | none | \((0,-a),(0, a)\) |
| Rectangle | Use \(( \pm a, 0)(0, \pm b)\) | Use \((0, \pm a)( \pm b, 0)\) |
| Asymptotes | \(y=\frac{b}{a} x, y=-\frac{b}{a} x\) | \(y=\frac{a}{b} x, y=-\frac{a}{b} x\) |
We will use these properties to graph hyperbolas.
Graph \(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\).
Solution:
| Step 1: Write the equation in standard form. | The equation is in standard form. | \(\frac{x^{2}}{25}-\frac{y^{2}}{4}=1\) |
| Step 2: Determine whether the transverse axis is horizontal or vertical. | Since the \(x^{2}\)-term is positive, the transverse axis is horizontal. | The transverse axis is horizontal. |
| Step 3: Find the vertices. | Since \(a^{2}=25\) then \(a=\pm 5\). The vertices are on the \(x\)-axis. | \((-5,0),(5,0)\) |
| Step 4: Sketch the rectangle centered at the origin intersection one axis at \(\pm a\) and the other at \(\pm b\). |
Since \(a=\pm 5\), the rectangle will intersect the \(x\)-axis at the vertices. Since \(b=\pm 2\), the rectangle will intersect the \(y\)-axis at \((0,-2)\) and \((0,2)\). |
.png?revision=1) |
|
Step 5: Sketch the asymptotes--the lines through the diagonals of the rectangle. |
The asymptotes have the equations \(y=\frac{5}{2} x, y=-\frac{5}{2} x\). | .png?revision=1) |
| Step 6: Draw the two branches of the hyperbola. | Start at each vertex and use the asymptotes as a guide. | 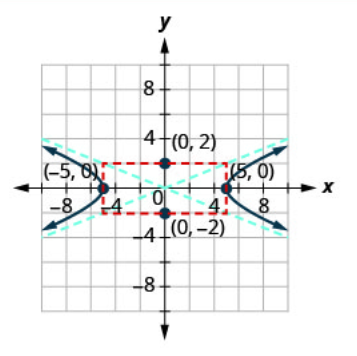.png?revision=1) |
Graph \(\frac{x^{2}}{16}-\frac{y^{2}}{4}=1\).
- Answer
-
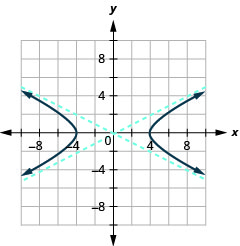
Figure 11.4.9
Graph \(\frac{x^{2}}{9}-\frac{y^{2}}{16}=1\).
- Answer
-
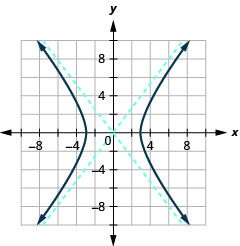
Figure 11.4.10
We summarize the steps for reference.
Graph a Hyperbola Centered at \((0,0)\)
- Write the equation in standard form.
- Determine whether the transverse axis is horizontal or vertical.
- Find the vertices.
- Sketch the rectangle centered at the origin intersecting one axis at \(±a\) and the other at \(±b\).
- Sketch the asymptotes—the lines through the diagonals of the rectangle.
- Draw the two branches of the hyperbola.
Sometimes the equation for a hyperbola needs to be first placed in standard form before we graph it.
Graph \(4 y^{2}-16 x^{2}=64\).
Solution:
| \(4 y^{2}-16 x^{2}=64\) | |
| To write the equation in standard form, divide each term by \(64\) to make the equation equal to \(1\). | \(\frac{4 y^{2}}{64}-\frac{16 x^{2}}{64}=\frac{64}{64}\) |
| Simplify. | \(\frac{y^{2}}{16}-\frac{x^{2}}{4}=1\) |
| Since the \(y^{2}\)-term is positive, the transverse axis is vertical. Since \(a^{2}=16\) then \(a=\pm 4\). | |
| The vertices are on the \(y\)-axis, \((0,-a),(0, a)\). Since \(b^{2}=4\) then \(b=\pm 2\). | \((0,-4),(0,4)\) |
| Sketch the rectangle intersecting the \(x\)-axis at \((-2,0),(2,0)\) and the \(y\)-axis at the vertices. Sketch the asymptotes through the diagonals of the rectangle. Draw the two branches of the hyperbola. | 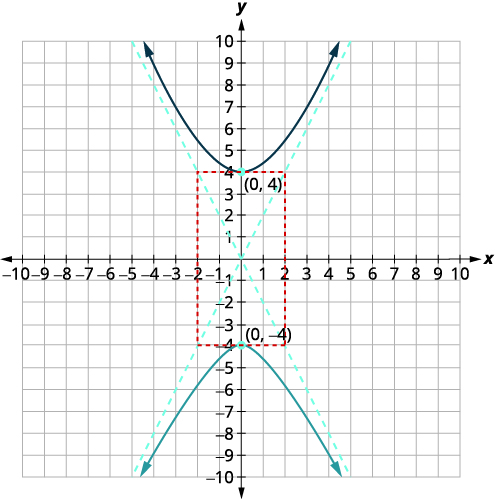 |
Graph \(4 y^{2}-25 x^{2}=100\).
- Answer
-
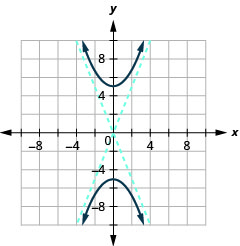
Figure 11.4.12
Graph \(25 y^{2}-9 x^{2}=225\).
- Answer
-
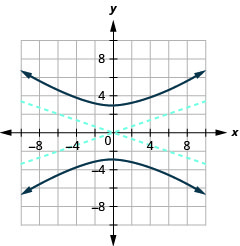
Figure 11.4.13
Graph a Hyperbola with Center at \((h,k)\)
Hyperbolas are not always centered at the origin. When a hyperbola is centered at \((h,k)\) the equations changes a bit as reflected in the table.
Standard Forms of the Equation a Hyperbola with Center \((h,k)\)
| \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) | \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\) | |
|---|---|---|
| Orientation | Transverse axis is horizontal. Opens left and right | Transverse axis is vertical. Opens up and down |
| Center | \((h,k)\) | \((h,k)\) |
| Vertices | \(a\) units to the left and right of the center | \(a\) units above and below the center |
| Rectangle | Use \(a\) units left/right of center \(b\) units above/below the center | Use \(a\) units above/below the center \(b\) units left/right of center |
Graph \(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\)
Solution:
| Step 1: Write the equation in standard form. | The equation is in standard form. | \(\frac{(x-1)^{2}}{9}-\frac{(y-2)^{2}}{16}=1\) |
| Step 2: Determine whether the transverse axis is horizontal or vertical. | Since the \(x^{2}\)-term is positive, the hyperbola opens left and right. | The transverse axis is horizontal. The hyperbola opens left and right. |
| Step 3: Find the center and \(a, b\). | \(h=1\) and \(k=2\) \(a^{2}=9\) \(b^{2}=16\) |
\(\begin{array} {c} \frac{\left(\stackrel{\color{red}{x-h}}{\color{black}{x-1}} \right)^{2}}{9} - \frac{\left(\stackrel{\color{red}{y-k}}{\color{black}{y-2}} \right)^{2}}{16} = 1 \end{array}\) Center: \((1,2)\) \(a=3\) \(b=4\) |
| Step 4: Sketch the rectangle centered at \((h,k)\) using \(a,b\). |
Mark the center, \((1,2)\). Sketch the rectangle that goes through the points \(3\) units to the left/right of the center and \(4\) units above and below the center. |
.png?revision=1) |
| Step 5: Sketch the asymptotes--the lines through the diagonals of the rectangle. Mark the vertices. | Sketch the diagonals. Mark the vertices, which are on the rectangle \(3\) units to the left and right of the center. | .png?revision=1) |
| Step 6: Draw the two branches of the hyperbola. | Start at each vertex and use the asymptotes as a guide. | .png?revision=1) |
Graph \(\frac{(x-3)^{2}}{25}-\frac{(y-1)^{2}}{9}=1\).
- Answer
-
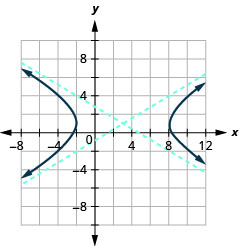
Figure 11.4.17
Graph \(\frac{(x-2)^{2}}{4}-\frac{(y-2)^{2}}{9}=1\).
- Answer
-
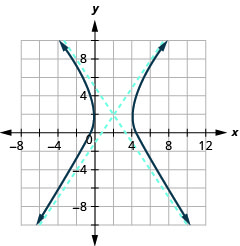
Figure 11.4.18
We summarize the steps for easy reference.
Graph a Hyperbola Centered at \((h,k)\)
- Write the equation in standard form.
- Determine whether the transverse axis is horizontal or vertical.
- Find the center and \(a,b\).
- Sketch the rectangle centered at \((h,k)\) using \(a,b\).
- Sketch the asymptotes—the lines through the diagonals of the rectangle. Mark the vertices.
- Draw the two branches of the hyperbola.
Be careful as you identify the center. The standard equation has \(x−h\) and \(y−k\) with the center as \((h,k)\).
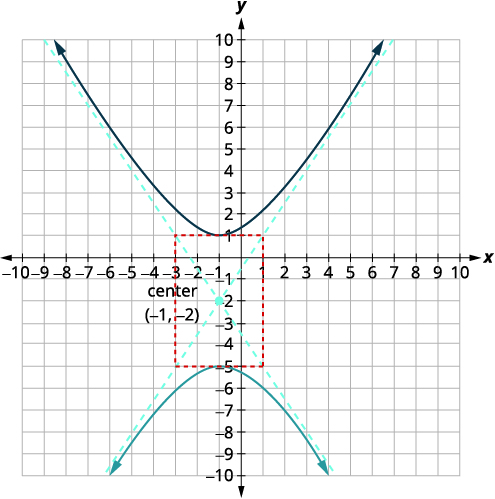
Graph \(\frac{(y+2)^{2}}{9}-\frac{(x+1)^{2}}{4}=1\).
Solution:
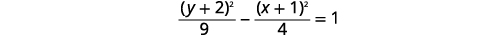 |
|
| Since the \(y^{2}\)-term is positive, the hyperbola opens up and down. | 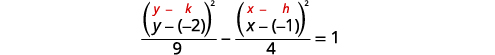 |
| Find the center, \((h,k)\). | Center: \((-1,-2)\) |
| Find \(a,b\). | \(a=3 b=2\) |
| Sketch the rectangle that goes through the points \(3\) units above and below the center and \(2\) units to the left/right of the center. Sketch the asymptotes—the lines through the diagonals of the rectangle. Mark the vertices. Graph the branches. |
 |
Graph \(\frac{(y+3)^{2}}{16}-\frac{(x+2)^{2}}{9}=1\).
- Answer
-
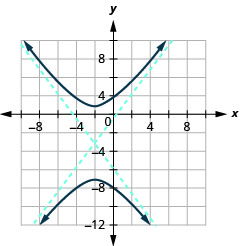
Figure 11.4.22
Graph \(\frac{(y+2)^{2}}{9}-\frac{(x+2)^{2}}{9}=1\).
- Answer
-
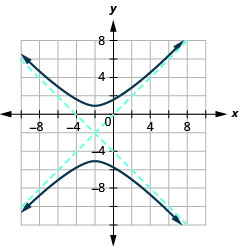
Figure 11.4.23
Again, sometimes we have to put the equation in standard form as our first step.
Write the equation in standard form and graph \(4 x^{2}-9 y^{2}-24 x-36 y-36=0\).
Solution:
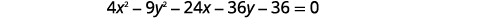 |
|
| To get to standard form, complete the squares. | 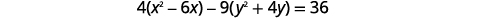 |
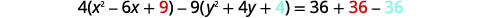 |
|
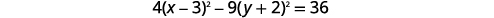 |
|
| Divide each term by \(36\) to get the constant to be \(1\). | 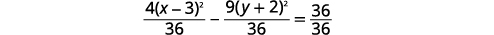 |
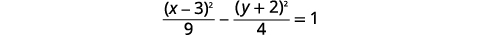 |
|
| Since the \(x^{2}\)-term is positive, the hyperbola opens left and right. | |
| Find the center, \((h,k)\). | Center: \((3, -2)\) |
| Find \(a,b\). |
\(a=3\) \(b=4\) |
| Sketch the rectangle that goes through the points \(3\) units to the left/right of the center and \(2\) units above and below the center. Sketch the asymptotes—the lines through the diagonals of the rectangle. Mark the vertices. Graph the branches. |
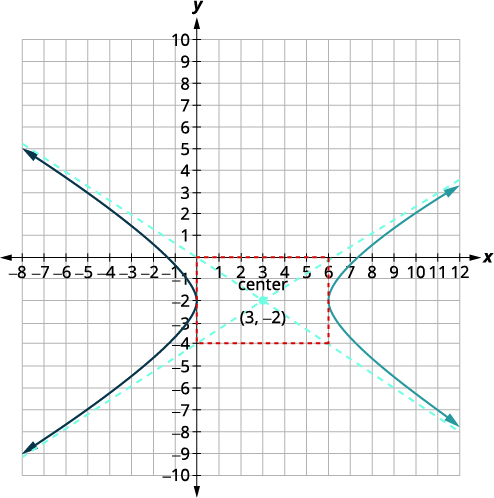 |
- Write the equation in standard form and
- Graph \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\).
- Answer
-
- \(\frac{(x+1)^{2}}{16}-\frac{(y-2)^{2}}{9}=1\)
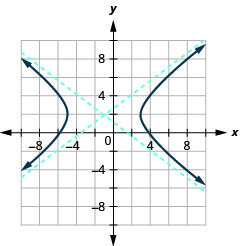
Figure 11.4.31
- Write the equation in standard form and
- Graph \(16 x^{2}-25 y^{2}+96 x-50 y-281=0\).
- Answer
-
- \(\frac{(x+3)^{2}}{25}-\frac{(y+1)^{2}}{16}=1\)
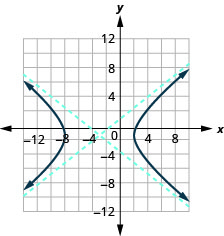
Figure 11.4.32
Identify Conic Sections by Their Equations
Now that we have completed our study of the conic sections, we will take a look at the different equations and recognize some ways to identify a conic by its equation. When we are given an equation to graph, it is helpful to identify the conic so we know what next steps to take.
To identify a conic from its equation, it is easier if we put the variable terms on one side of the equation and the constants on the other.
| Conic | Characteristics of \(x^{2}\)- and \(y^{2}\)-terms | Example |
|---|---|---|
| Parabola | Either \(x^{2}\) OR \(y^{2}\). Only one variable is squared. | \(x=3 y^{2}-2 y+1\) |
| Circle | \(x^{2}\)- and \(y^{2}\)- terms have the same coefficients. | \(x^{2}+y^{2}=49\) |
| Ellipse | \(x^{2}\)- and \(y^{2}\)- terms have the same sign, different coefficients. | \(4 x^{2}+25 y^{2}=100\) |
| Hyperbola | \(x^{2}\)- and \(y^{2}\)- terms have the different signs, different coefficients. | \(25 y^{2}-4 x^{2}=100\) |
Identify the graph of each equation as a circle, parabola, ellipse, or hyperbola.
- \(9 x^{2}+4 y^{2}+56 y+160=0\)
- \(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)
- \(x^{2}+y^{2}-6 x-8 y=0\)
- \(y=-2 x^{2}-4 x-5\)
Solution:
a. The \(x^{2}\)- and \(y^{2}\)-terms have the same sign and different coefficients.
\(9 x^{2}+4 y^{2}+56 y+160=0\)
Ellipse
b. The \(x^{2}\)- and \(y^{2}\)-terms have different signs and different coefficients.
\(9 x^{2}-16 y^{2}+18 x+64 y-199=0\)
Hyperbola
c. The \(x^{2}\)- and \(y^{2}\)-terms have the same coefficients.
\(x^{2}+y^{2}-6 x-8 y=0\)
Circle
d. Only one variable, \(x\), is squared.
\(y=-2 x^{2}-4 x-5\)
Parabola
Identify the graph of each equation as a circle, parabola, ellipse, or hyperbola.
- \(x^{2}+y^{2}-8 x-6 y=0\)
- \(4 x^{2}+25 y^{2}=100\)
- \(y=6 x^{2}+2 x-1\)
- \(16 y^{2}-9 x^{2}=144\)
- Answer
-
- Circle
- Ellipse
- Parabola
- Hyperbola
Identify the graph of each equation as a circle, parabola, ellipse, or hyperbola.
- \(16 x^{2}+9 y^{2}=144\)
- \(y=2 x^{2}+4 x+6\)
- \(x^{2}+y^{2}+2 x+6 y+9=0\)
- \(4 x^{2}-16 y^{2}=64\)
- Answer
-
- Ellipse
- Parabola
- Circle
- Hyperbola
Access these online resources for additional instructions and practice with hyperbolas.
- Graph a Hyperbola with Center at the Origin
- Graph a Hyperbola with Center not at the Origin
- Graph a Hyperbola in General Form
- Identifying Conic Sections in General Form
Key Concepts
- Hyperbola: A hyperbola is all points in a plane where the difference of their distances from two fixed points is constant.
- Each of the fixed points is called a focus of the hyperbola.
The line through the foci, is called the transverse axis.
The two points where the transverse axis intersects the hyperbola are each a vertex of the hyperbola.
The midpoint of the segment joining the foci is called the center of the hyperbola.
The line perpendicular to the transverse axis that passes through the center is called the conjugate axis.
Each piece of the graph is called a branch of the hyperbola.
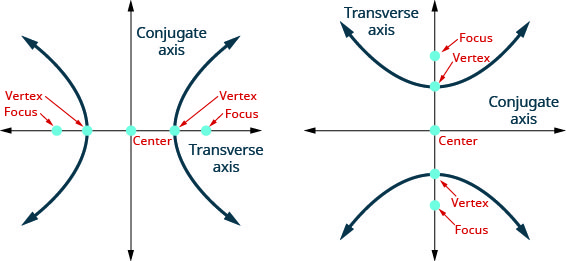
Figure 11.4.2
Standard Forms of the Equation a Hyperbola with Center \((0,0)\)
| \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\) | \(\frac{y^{2}}{a^{2}}-\frac{x^{2}}{b^{2}}=1\) | |
|---|---|---|
| Orientation | Transverse axis on the \(x\)-axis. Opens left and right |
Transverse axis on the \(y\)-axis. Opens up and down |
| Vertices | \((-a, 0),(a, 0)\) | \((0,-a),(0, a)\) |
| \(x\)-intercepts | \((-a, 0),(a, 0)\) | none |
| \(y\)-intercepts | none | \((0,-a),(0, a)\) |
| Rectangle | Use \(( \pm a, 0)(0, \pm b)\) | Use \((0, \pm a)( \pm b, 0)\) |
| Asymptotes | \(y=\frac{b}{a} x, y=-\frac{b}{a} x\) | \(y=\frac{a}{b} x, y=-\frac{a}{b} x\) |
- How to graph a hyperbola centered at \((0,0)\).
- Write the equation in standard form.
- Determine whether the transverse axis is horizontal or vertical.
- Find the vertices.
- Sketch the rectangle centered at the origin intersecting one axis at \(±a\) and the other at \(±b\).
- Sketch the asymptotes—the lines through the diagonals of the rectangle.
- Draw the two branches of the hyperbola.
Standard Forms of the Equation a Hyperbola with Center \((h,k)\)
| \(\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1\) | \(\frac{(y-k)^{2}}{a^{2}}-\frac{(x-h)^{2}}{b^{2}}=1\) | |
|---|---|---|
| Orientation | Transverse axis is horizontal. Opens left and right | Transverse axis is vertical. Opens up and down |
| Center | \((h,k)\) | \((h,k)\) |
| Vertices | \(a\) units to the left and right of the center | \(a\) units above and below the center |
| Rectangle | Use \(a\) units left/right of center \(b\) units above/below the center | Use \(a\) units above/below the center \(b\) units left/right of center |
- How to graph a hyperbola centered at \((h,k)\).
- Write the equation in standard form.
- Determine whether the transverse axis is horizontal or vertical.
- Find the center and \(a,b\).
- Sketch the rectangle centered at \((h,k)\) using \(a,b\).
- Sketch the asymptotes—the lines through the diagonals of the rectangle. Mark the vertices.
- Draw the two branches of the hyperbola.
| Conic | Characteristics of \(x^{2}\)- and \(y^{2}\)-terms | Example |
|---|---|---|
| Parabola | Either \(x^{2}\) OR \(y^{2}\). Only one variable is squared. | \(x=3 y^{2}-2 y+1\) |
| Circle | \(x^{2}\)- and \(y^{2}\)- terms have the same coefficients. | \(x^{2}+y^{2}=49\) |
| Ellipse | \(x^{2}\)- and \(y^{2}\)- terms have the same sign, different coefficients. | \(4 x^{2}+25 y^{2}=100\) |
| Hyperbola | \(x^{2}\)- and \(y^{2}\)- terms have the different signs, different coefficients. | \(25 y^{2}-4 x^{2}=100\) |
Glossary
- hyperbola
- A hyperbola is defined as all points in a plane where the difference of their distances from two fixed points is constant.


