Chapter 11 Review Exercises
( \newcommand{\kernel}{\mathrm{null}\,}\)
Chapter Review Exercises
Distance and Midpoint Formulas; Circles
In the following exercises, find the distance between the points. Round to the nearest tenth if needed.
- (−5,1) and (−1,4)
- (−2,5) and (1,5)
- (8,2) and (−7,−3)
- (1,−4) and (5,−5)
- Answer
-
2. d=3
4. d=√17,d≈4.1
In the following exercises, find the midpoint of the line segments whose endpoints are given.
- (−2,−6) and (−4,−2)
- (3,7) and (5,1)
- (−8,−10) and (9,5)
- (−3,2) and (6,−9)
- Answer
-
2. (4,4)
4. (32,−72)
In the following exercises, write the standard form of the equation of the circle with the given information.
- radius is 15 and center is (0,0)
- radius is √7 and center is (0,0)
- radius is 9 and center is (−3,5)
- radius is 7 and center is (−2,−5)
- center is (3,6) and a point on the circle is (3,−2)
- center is (2,2) and a point on the circle is (4,4)
- Answer
-
2. x2+y2=7
4. (x+2)2+(y+5)2=49
6. (x−2)2+(y−2)2=8
In the following exercises,
- Find the center and radius, then
- Graph each circle.
- 2x2+2y2=450
- 3x2+3y2=432
- (x+3)2+(y−5)2=81
- (x+2)2+(y+5)2=49
- x2+y2−6x−12y−19=0
- x2+y2−4y−60=0
- Answer
-
2.
- radius: 12, center: (0,0)
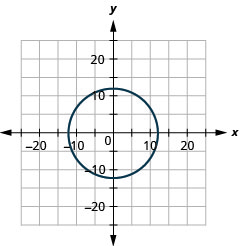
Figure 11.E.1 4.
- radius: 7, center: (−2,−5)
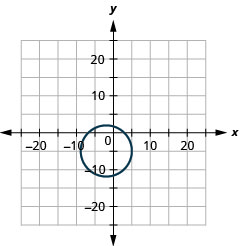
Figure 11.E.2 6.
- radius: 8, center: (0,2)
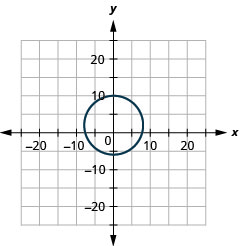
Figure 11.E.3
Parabolas
In the following exercises, graph each equation by using its properties.
- y=x2+4x−3
- y=2x2+10x+7
- y=−6x2+12x−1
- y=−x2+10x
- Answer
-
2.
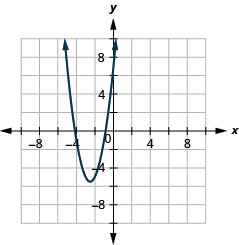
Figure 11.E.4 4.
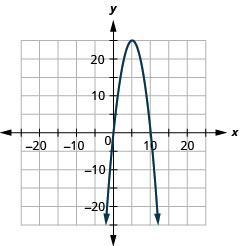
Figure 11.E.5
In the following exercises,
- Write the equation in standard form, then
- Use properties of the standard form to graph the equation.
- y=x2+4x+7
- y=2x2−4x−2
- y=−3x2−18x−29
- y=−x2+12x−35
- Answer
-
2.
- y=2(x−1)2−4
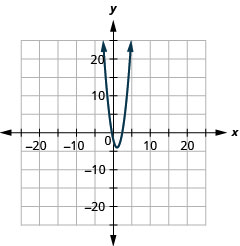
Figure 11.E.6 4.
- y=−(x−6)2+1
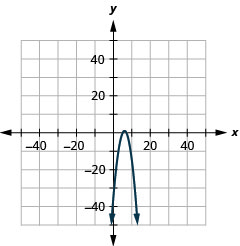
Figure 11.E.7
In the following exercises, graph each equation by using its properties.
- x=2y2
- x=2y2+4y+6
- x=−y2+2y−4
- x=−3y2
- Answer
-
2.
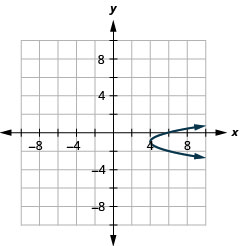
Figure 11.E.8 4.
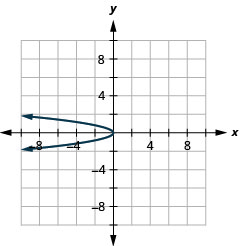
Figure 11.E.9
In the following exercises,
- Write the equation in standard form, then
- Use properties of the standard form to graph the equation.
- x=4y2+8y
- x=y2+4y+5
- x=−y2−6y−7
- x=−2y2+4y
- Answer
-
2.
- x=(y+2)2+1
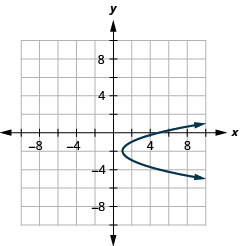
Figure 11.E.10 4.
- x=−2(y−1)2+2
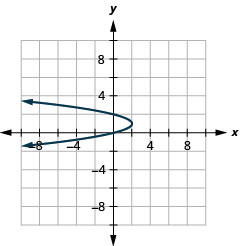
Figure 11.E.11
In the following exercises, create the equation of the parabolic arch formed in the foundation of the bridge shown. Give the answer in standard form.
1.
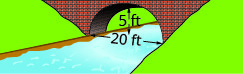
2.
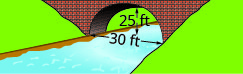
- Answer
-
2. y=−19x2+103x
Ellipses
In the following exercises, graph each ellipse.
- x236+y225=1
- x24+y281=1
- 49x2+64y2=3136
- 9x2+y2=9
- Answer
-
2.
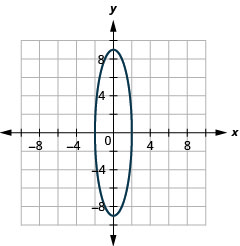
Figure 11.E.14 4.
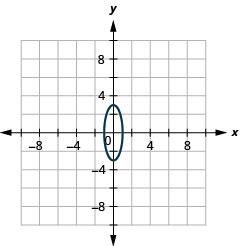
Figure 11.E.15
In the following exercises, find the equation of the ellipse shown in the graph.
1.
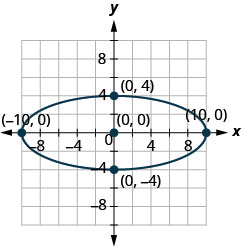
2.
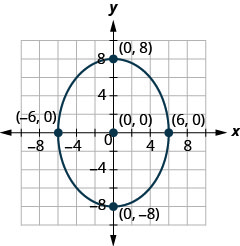
- Answer
-
2. x236+y264=1
In the following exercises, graph each ellipse.
- (x−1)225+(y−6)24=1
- (x+4)216+(y+1)29=1
- (x−5)216+(y+3)236=1
- (x+3)29+(y−2)225=1
- Answer
-
2.
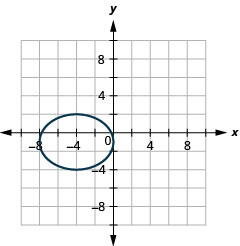
Figure 11.E.18 4.
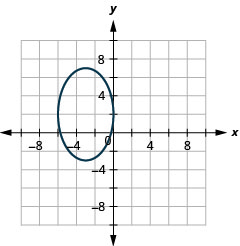
Figure 11.E.19
In the following exercises,
- Write the equation in standard form and
- Graph.
- x2+y2+12x+40y+120=0
- 25x2+4y2−150x−56y+321=0
- 25x2+4y2+150x+125=0
- 4x2+9y2−126x+405=0
- Answer
-
2.
- (x−3)24+(y−7)225=1
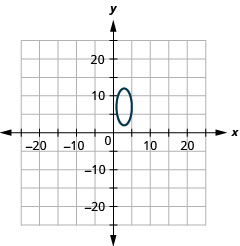
Figure 11.E.20 4.
- x29+(y−7)24=1
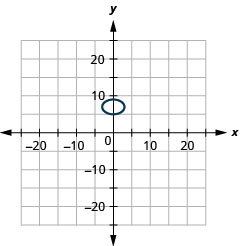
Figure 11.E.21
In the following exercises, write the equation of the ellipse described.
- A comet moves in an elliptical orbit around a sun. The closest the comet gets to the sun is approximately 10 AU and the furthest is approximately 90 AU. The sun is one of the foci of the elliptical orbit. Letting the ellipse center at the origin and labeling the axes in AU, the orbit will look like the figure below. Use the graph to write an equation for the elliptical orbit of the comet.
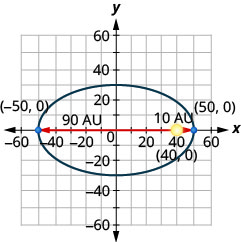
- Answer
-
1. Solve
Hyperbolas
In the following exercises, graph.
- x225−y29=1
- y249−x216=1
- 9y2−16x2=144
- 16x2−4y2=64
- Answer
-
1.
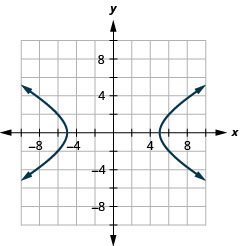
Figure 11.E.23 3.
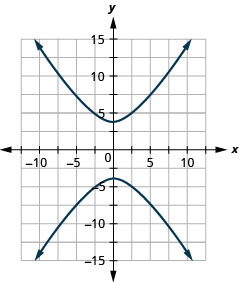
Figure 11.E.24
In the following exercises, graph.
- (x+1)24−(y+1)29=1
- (x−2)24−(y−3)216=1
- (y+2)29−(x+1)29=1
- (y−1)225−(x−2)29=1
- Answer
-
1.
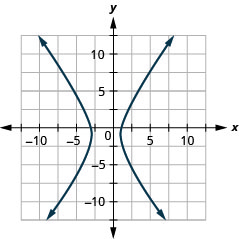
Figure 11.E.25 3.
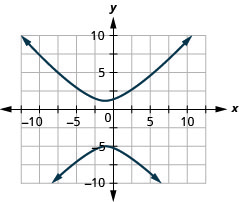
Figure 11.E.26
In the following exercises,
- Write the equation in standard form and
- Graph.
- 4x2−16y2+8x+96y−204=0
- 16x2−4y2−64x−24y−36=0
- 4y2−16x2+32x−8y−76=0
- 36y2−16x2−96x+216y−396=0
- Answer
-
1.
- (x+1)216−(y−3)24=1
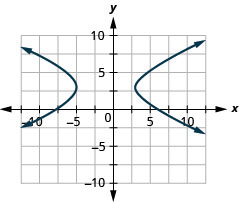
Figure 11.E.27 3.
- (y−1)216−(x−1)24=1
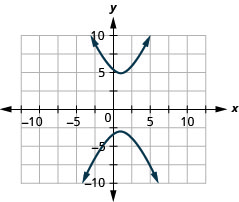
Figure 11.E.28
In the following exercises, identify the type of graph.
-
- 16y2−9x2−36x−96y−36=0
- x2+y2−4x+10y−7=0
- y=x2−2x+3
- 25x2+9y2=225
-
- x2+y2+4x−10y+25=0
- y2−x2−4y+2x−6=0
- x=−y2−2y+3
- 16x2+9y2=144
- Answer
-
1.
- Hyperbola
- Circle
- Parabola
- Ellipse
Solve Systems of Nonlinear Equations
In the following exercises, solve the system of equations by using graphing.
- {3x2−y=0y=2x−1
- {y=x2−4y=x−4
- {x2+y2=169x=12
- {x2+y2=25y=−5
- Answer
-
1.
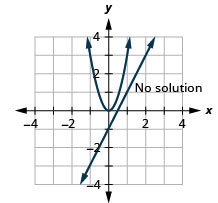
Figure 11.E.29 3.
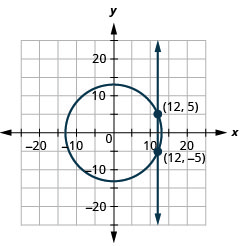
Figure 11.E.30
In the following exercises, solve the system of equations by using substitution.
- {y=x2+3y=−2x+2
- {x2+y2=4x−y=4
- {9x2+4y2=36y−x=5
- {x2+4y2=42x−y=1
- Answer
-
1. (−1,4)
3. No solution
In the following exercises, solve the system of equations by using elimination.
- {x2+y2=16x2−2y−1=0
- {x2−y2=5−2x2−3y2=−30
- {4x2+9y2=363y2−4x=12
- {x2+y2=14x2−y2=16
- Answer
-
1. (−√7,3),(√7,3)
3. (−3,0),(0,−2),(0,2)
In the following exercises, solve the problem using a system of equations.
- The sum of the squares of two numbers is 25. The difference of the numbers is 1. Find the numbers.
- The difference of the squares of two numbers is 45. The difference of the square of the first number and twice the square of the second number is 9. Find the numbers.
- The perimeter of a rectangle is 58 meters and its area is 210 square meters. Find the length and width of the rectangle.
- Colton purchased a larger microwave for his kitchen. The diagonal of the front of the microwave measures 34 inches. The front also has an area of 480 square inches. What are the length and width of the microwave?
- Answer
-
1. −3 and −4 or 4 and 3
3. If the length is 14 inches, the width is 15 inches. If the length is 15 inches, the width is 14 inches.
Practice Test
In the following exercises, find the distance between the points and the midpoint of the line segment with the given endpoints. Round to the nearest tenth as needed.
- (−4,−3) and (−10,−11)
- (6,8) and (−5,−3)
- Answer
-
1. distance: 10, midpoint: (−7,−7)
In the following exercises, write the standard form of the equation of the circle with the given information.
- radius is 11 and center is (0,0)
- radius is 12 and center is (10,−2)
- center is (−2,3) and a point on the circle is (2,−3)
- Find the equation of the ellipse shown in the graph.
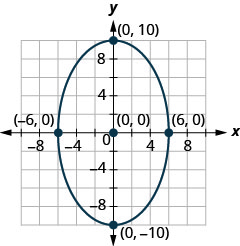
- Answer
-
1. x2+y2=121
3. (x+2)2+(y−3)2=52
In the following exercises,
- Identify the type of graph of each equation as a circle, parabola, ellipse, or hyperbola, and
- Graph the equation.
- 4x2+49y2=196
- y=3(x−2)2−2
- 3x2+3y2=27
- y2100−x236=1
- x216+y281=1
- x=2y2+10y+7
- 64x2−9y2=576
- Answer
-
1.
- Ellipse
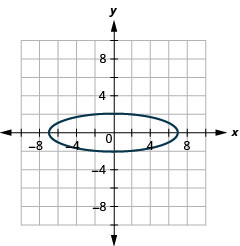
Figure 11.E.32 3.
- Circle
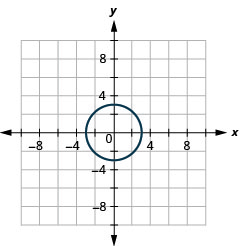
Figure 11.E.33 5.
- Ellipse
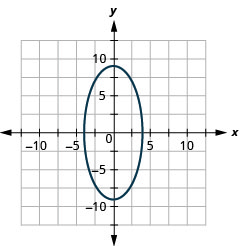
Figure 11.E.34 7.
- Hyperbola
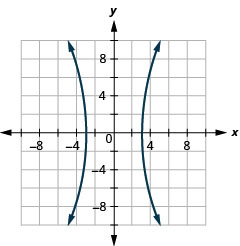
Figure 11.E.35
In the following exercises,
- Identify the type of graph of each equation as a circle, parabola, ellipse, or hyperbola,
- Write the equation in standard form, and
- Graph the equation.
- 25x2+64y2+200x−256y−944=0
- x2+y2+10x+6y+30=0
- x=−y2+2y−4
- 9x2−25y2−36x−50y−214=0
- y=x2+6x+8
- Solve the nonlinear system of equations by graphing: {3y2−x=0y=−2x−1.
- Solve the nonlinear system of equations using substitution: {x2+y2=8y=−x−4.
- Solve the nonlinear system of equations using elimination: {x2+9y2=92x2−9y2=18
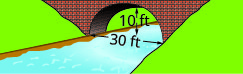
- Create the equation of the parabolic arch formed in the foundation of the bridge shown. Give the answer in y=ax2+bx+c form.
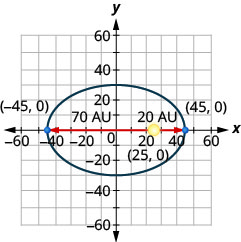
10. A comet moves in an elliptical orbit around a sun. The closest the comet gets to the sun is approximately 20 AU and the furthest is approximately 70 AU. The sun is one of the foci of the elliptical orbit. Letting the ellipse center at the origin and labeling the axes in AU, the orbit will look like the figure below. Use the graph to write an equation for the elliptical orbit of the comet.
11. The sum of two numbers is 22 and the product is −240. Find the numbers.
12. For her birthday, Olive’s grandparents bought her a new widescreen TV. Before opening it she wants to make sure it will fit her entertainment center. The TV is 55”. The size of a TV is measured on the diagonal of the screen and a widescreen has a length that is larger than the width. The screen also has an area of 1452 square inches. Her entertainment center has an insert for the TV with a length of 50 inches and width of 40 inches. What are the length and width of the TV screen and will it fit Olive’s entertainment center?
- Answer
-
2.
- Circle
- (x+5)2+(y+3)2=4
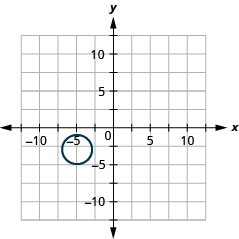
Figure 11.E.38 4.
- Hyperbola
- (x−2)225−(y+1)29=1
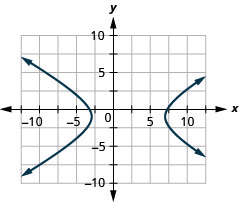
Figure 11.E.39 6. No solution
8. (0,−3),(0,3)
10. x22025+y21400=1
12. The length is 44 inches and the width is 33 inches. The TV will fit Olive’s entertainment center.
Glossary
- system of nonlinear equations
- A system of nonlinear equations is a system where at least one of the equations is not linear.


