7.7: Solve Rational Inequalities
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Solve rational inequalities
- Solve an inequality with rational functions
Before you get started, take this readiness quiz.
- Find the value of x−5 when ⓐ x=6 ⓑ x=−3 ⓒ x=5
If you missed this problem, review Example 1.2.16. - Solve: 8−2x<12
If you missed this problem, review Example 2.6.13. - Write in interval notation: −3≤x<5
If you missed this problem, review Example 2.6.4.
Solve Rational Inequalities
We learned to solve linear inequalities after learning to solve linear equations. The techniques were very much the same with one major exception. When we multiplied or divided by a negative number, the inequality sign reversed.
Having just learned to solve rational equations we are now ready to solve rational inequalities. A rational inequality is an inequality that contains a rational expression.
A rational inequality is an inequality that contains a rational expression.
Inequalities such as32x>1,2xx−3<4,2x−3x−6≥x, and 14−2x2≤3x are rational inequalities as they each contain a rational expression.
When we solve a rational inequality, we will use many of the techniques we used solving linear inequalities. We especially must remember that when we multiply or divide by a negative number, the inequality sign must reverse.
Another difference is that we must carefully consider what value might make the rational expression undefined and so must be excluded.
When we solve an equation and the result is x=3, we know there is one solution, which is 3.
When we solve an inequality and the result is x>3, we know there are many solutions. We graph the result to better help show all the solutions, and we start with 3. Three becomes a critical point and then we decide whether to shade to the left or right of it. The numbers to the right of 3 are larger than 3, so we shade to the right.

To solve a rational inequality, we first must write the inequality with only one quotient on the left and 0 on the right.
Next we determine the critical points to use to divide the number line into intervals. A critical point is a number which make the rational expression zero or undefined.
We then will evaluate the factors of the numerator and denominator, and find the quotient in each interval. This will identify the interval, or intervals, that contains all the solutions of the rational inequality.
We write the solution in interval notation being careful to determine whether the endpoints are included.
Solve and write the solution in interval notation: x−1x+3≥0
Solution
Step 1. Write the inequality as one quotient on the left and zero on the right.
Our inequality is in this form.x−1x+3≥0
Step 2. Determine the critical points—the points where the rational expression will be zero or undefined.
The rational expression will be zero when the numerator is zero. Since x−1=0 when x=1, then 1 is a critical point.
The rational expression will be undefined when the denominator is zero. Since x+3=0 when x=−3, then -3 is a critical point.
The critical points are 1 and -3.
Step 3. Use the critical points to divide the number line into intervals.
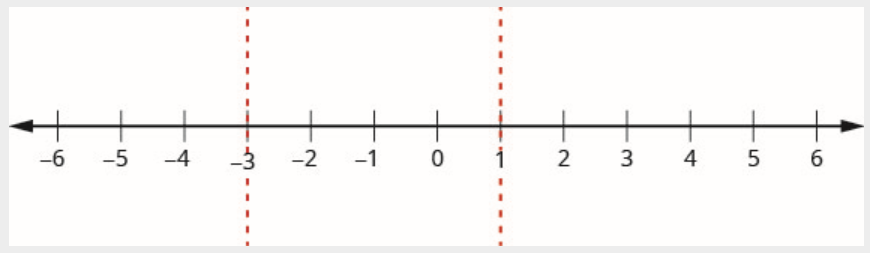
The number line is divided into three intervals:
(−∞,−3)(−3,1)(1,∞)
Step 4. Test a value in each interval. Above the number line show the sign of each factor of the rational expression in each interval. Below the number line show the sign of the quotient.
To find the sign of each factor in an interval, we choose any point in that interval and use it as a test point. Any point in the interval will give the expression the same sign, so we can choose any point in the interval.
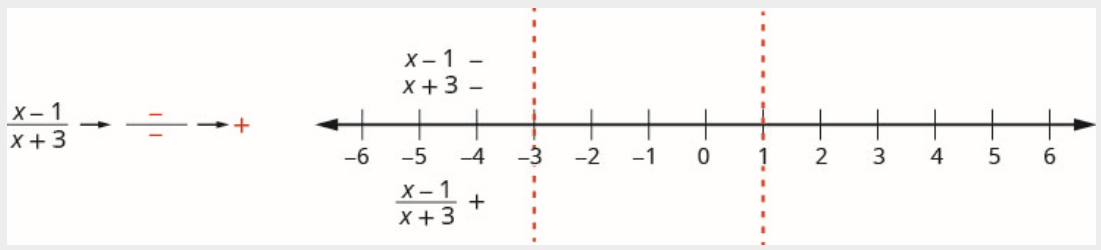
Interval (−∞,−3)
The number -4 is in the interval (−∞,−3). Test x=−4 in the expression in the numerator and the denominator.
The numerator:
x−1−4−1−5Negative
The denominator:
x+3−4+3−1Negative
Above the number line, mark the factor x−1 negative and mark the factor x+3 negative.
Since a negative divided by a negative is positive, mark the quotient positive in the interval (−∞,−3)
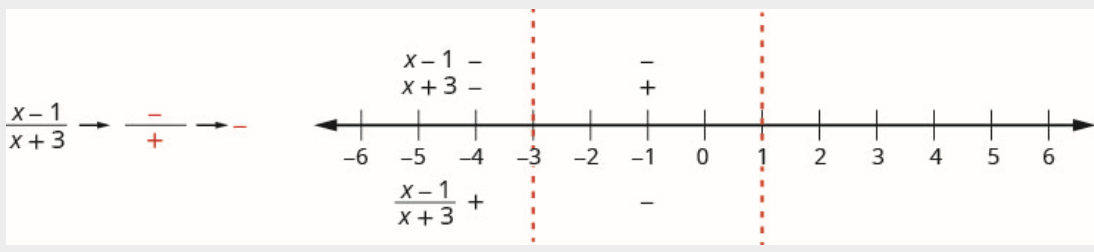
Interval (−3,1)
The number 0 is in the interval (−3,1). Test x=0.
The numerator:
x−10−1−1Negative
The denominator:
x+30+33Positive
Above the number line, mark the factor x−1 negative and mark x+3 positive.
Since a negative divided by a positive is negative, the quotient is marked negative in the interval (−3,1).
Interval (1,∞)
The number 2 is in the interval (1,∞). Test x=2.
The numerator:
x−12−11Positive
The denominator:
x+32+35Positive
Above the number line, mark the factor x−1 positive and mark x+3 positive.
Since a positive divided by a positive is positive, mark the quotient positive in the interval (1,∞).
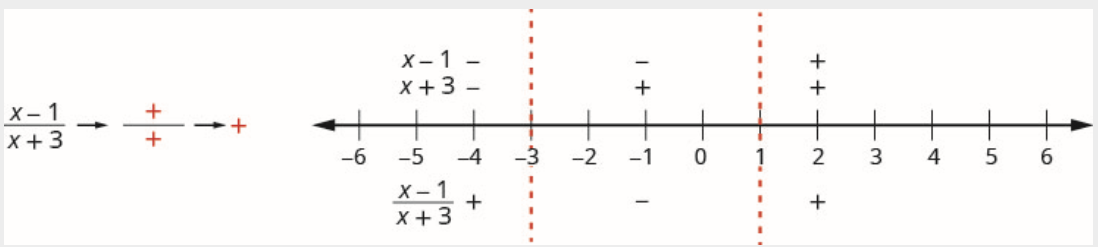
Step 5. Determine the intervals where the inequality is correct. Write the solution in interval notation.
We want the quotient to be greater than or equal to zero, so the numbers in the intervals (−∞,−3) and (1,∞)are solutions.
But what about the critical points?
The critical point x=−3 makes the denominator 0, so it must be excluded from the solution and we mark it with a parenthesis.
The critical point x=1 makes the whole rational expression 0. The inequality requires that the rational expression be greater than or equal to. So, 1 is part of the solution and we will mark it with a bracket.
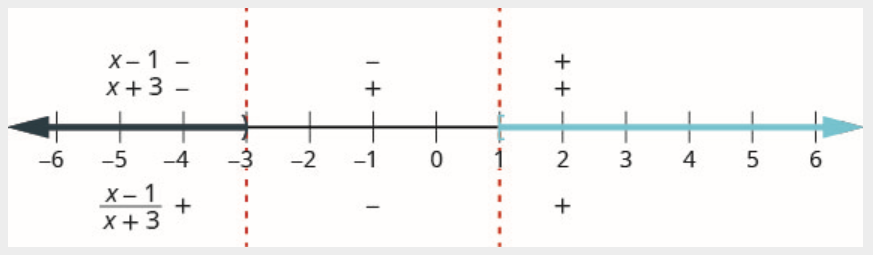
Recall that when we have a solution made up of more than one interval we use the union symbol, ∪, to connect the two intervals. The solution in interval notation is (−∞,−3)∪[1,∞).
Solve and write the solution in interval notation: x−2x+4≥0
- Answer
-
(−∞,−4)∪[2,∞)
Solve and write the solution in interval notation: x+2x−4≥0
- Answer
-
(−∞,−2]∪(4,∞)
We summarize the steps for easy reference.
Step 1. Write the inequality as one quotient on the left and zero on the right.
Step 2. Determine the critical points–the points where the rational expression will be zero or undefined.
Step 3. Use the critical points to divide the number line into intervals.
Step 4. Test a value in each interval. Above the number line show the sign of each factor of the numerator and denominator in each interval. Below the number line show the sign of the quotient.
Step 5. Determine the intervals where the inequality is correct. Write the solution in interval notation.
The next example requires that we first get the rational inequality into the correct form.
Solve and write the solution in interval notation: 4xx−6<1
Solution
4xx−6<1
Subtract 1 to get zero on the right.
4xx−6−1<0
Rewrite 1 as a fraction using the LCD.
4xx−6−x−6x−6<0
Subtract the numerators and place the difference over the common denominator.
4x−(x−6)x−6<0
Simplify.
3x+6x−6<0
Factor the numerator to show all factors.
3(x+2)x−6<0
Find the critical points.
The quotient will be zero when the numerator is zero. The quotient is undefined when the denominator is zero.
x+2=0x−6=0x=−2x=6
Use the critical points to divide the number line into intervals.

Test a value in each interval.
| (−∞,−2) | (−2,6) | (6,∞) | |
|---|---|---|---|
| x+2) |
x+2 -3+2 -1 - |
x+2 0+2 2 + |
x+2 7+2 9 + |
| x−6 |
x-6 -3-6 -9 - |
x-6 0-6 -6 - |
x-6 7-6 1 + |
Above the number line show the sign of each factor of the rational expression in each interval. Below the number line show the sign of the quotient.
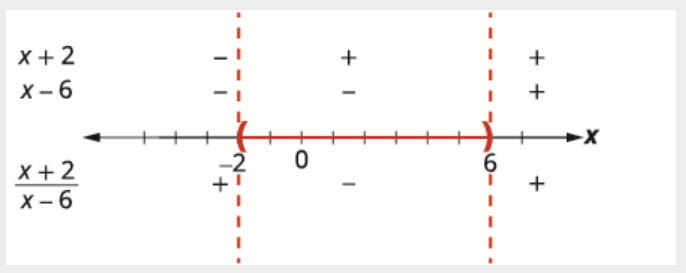
Determine the intervals where the inequality is correct. We want the quotient to be negative, so the solution includes the points between −2 and 6. Since the inequality is strictly less than, the endpoints are not included.
We write the solution in interval notation as (−2, 6).
Solve and write the solution in interval notation: 3xx−3<1.
- Answer
-
(−32,3)
Solve and write the solution in interval notation: 3xx−4<2.
- Answer
-
(−8,4)
In the next example, the numerator is always positive, so the sign of the rational expression depends on the sign of the denominator.
Solve and write the solution in interval notation: 5x2−2x−15>0.
Solution
The inequality is in the correct form.
5x2−2x−15>0
Factor the denominator.
5(x+3)(x−5)>0
Find the critical points. The quotient is 0 when the numerator is 0. Since the numerator is always 5, the quotient cannot be 0.
The quotient will be undefined when the denominator is zero.
(x+3)(x−5)=0x=−3,x=5
Use the critical points to divide the number line into intervals.
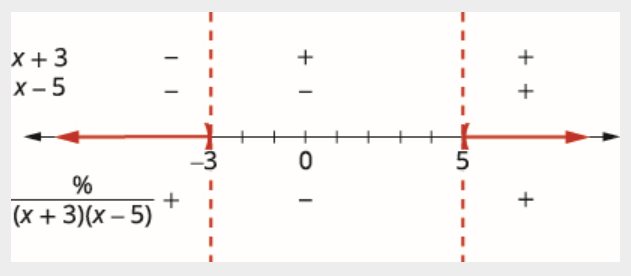
Test values in each interval. Above the number line show the sign of each factor of the denominator in each interval. Below the number line, show the sign of the quotient.
Write the solution in interval notation.
(−∞,−3)∪(5,∞)
Solve and write the solution in interval notation: 1x2+2x−8>0.
- Answer
-
(−∞,−4)∪(2,∞)
Solve and write the solution in interval notation: 3x2+x−12>0.
- Answer
-
(−∞,−4)∪(3,∞)
The next example requires some work to get it into the needed form.
Solve and write the solution in interval notation: 13−2x2<53x.
Solution
13−2x2<53x
Subtract 53x to get zero on the right.
13−2x2−53x<0
Rewrite to get each fraction with the LCD
1⋅x23⋅x2−2⋅3x2⋅3−5⋅x3x−x<0
Simplify.
x23x2−63x2−5x3x2<0
Subtract the numerators and place the difference over the common denominator.
x2−5x−63x2<0
Factor the numerator.
(x−6)(x+1)3x2<0
Find the critical points.
3x2=0x−6=0x+1=0x=0x=6x=−1
Use the critical points to divide the number line into intervals.
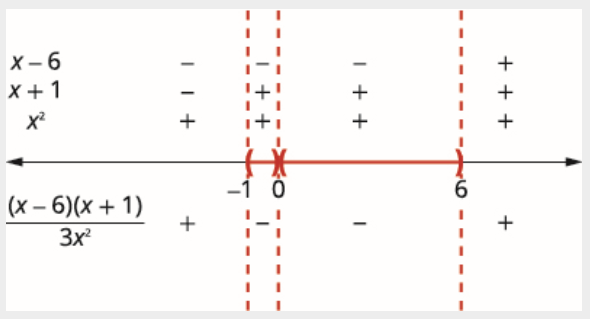
Above the number line show the sign of each factor in each interval. Below the number line, show the sign of the quotient.
Since, 0 is excluded, the solution is the two (−1,0)∪(0,6) intervals, (−1,0) and (0,6).
Solve and write the solution in interval notation: 12+4x2<3x.
- Answer
-
(2,4)
Solve and write the solution in interval notation: 13+6x2<3x.
- Answer
-
(3,6)
Solve an Inequality with Rational Functions
When working with rational functions, it is sometimes useful to know when the function is greater than or less than a particular value. This leads to a rational inequality.
Given the function R(x)=x+3x−5, find the values of x that make the function less than or equal to 0.
Solution
We want the function to be less than or equal to 0.
R(x)≤0
Substitute the rational expression for R(x).
x+3x−5≤0x≠5
Find the critical points.
x+3=0x−5=0x=−3x=5
Use the critical points to divide the number line into intervals.
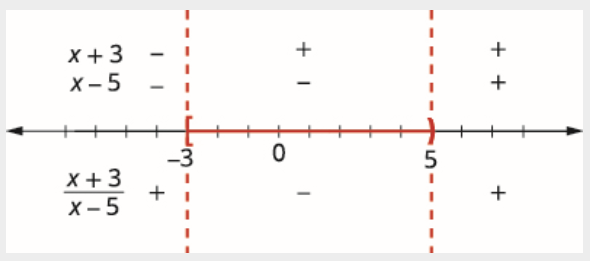
Test values in each interval. Above the number line, show the sign of each factor in each interval. Below the number line, show the sign of the quotient. Write the solution in interval notation. Since 5 is excluded we, do not include it in the interval.
[−3,5)
Given the function R(x)=x−2x+4, find the values of x that make the function less than or equal to 0.
- Answer
-
(−4,2]
Given the function R(x)=x+1x−4, find the values of x that make the function less than or equal to 0.
- Answer
-
[−1,4)
In economics, the function C(x) is used to represent the cost of producing x units of a commodity. The average cost per unit can be found by dividing C(x) by the number of items x. Then, the average cost per unit is \(c(x)=\dfrac{C(x)}{x}).
The functionC(x)=10x+3000 represents the cost to produce x, number of items. Find:
- The average cost function, c(x)
- How many items should be produced so that the average cost is less than $40.
Solution
- C(x)=10x+3000
The average cost function is c(x)=C(x)x). To find the average cost function, divide the cost function by x.
c(x)=C(x)xc(x)=10x+3000x
The average cost function is c(x)=10x+3000x
- We want the function c(x) to be less than 40.
c(x)<40
Substitute the rational expression forc(x).
10x+3000x<40,x≠0
Subtract 40 to get 0 on the right.
10x+3000x−40<0
Rewrite the left side as one quotient by finding the LCD and performing the subtraction.
10x+3000x−40(xx)<010x+3000x−40xx<010x+3000−40xx<0−30x+3000x<0
Factor the numerator to show all factors.
−30(x−100)x<0−30(x−100)=0x=0
Find the critical points.
−30≠0x−100=0x=100
More than 100 items must be produced to keep the average cost below $40 per item.
The functionC(x)=20x+6000 represents the cost to produce x, number of items. Find:
- How many items should be produced so that the average cost is less than $60.
- Answer
-
- c(x)=20x+6000x
- More than 150 items must be produced to keep the average cost below $60 per item.
The functionC(x)=5x+900 represents the cost to produce x, number of items. Find:
- How many items should be produced so that the average cost is less than $20.
- Answer
-
- c(x)=5x+900x
- More than 60 items must be produced to keep the average cost below $20 per item.


