5.1: Series

 

 

Series

---

Convergence of Sequences

An infinite sequence \(\left\{z_1,z_2,z_3 \ldots\right\}\) of complex numbers has a limit \(z\) if, for each positive number \(ε\), there exists a positive integer \(n_0\) such that

\(\begin{eqnarray}\label{seq}
                \left|z_n-z\right|< \varepsilon \quad \text{whenever}\quad n > n_0.
                \end{eqnarray}\)

Geometrically, this means that for sufficiently large values of \(n\), the points \(z_n\) lie in any given \(ε\) neighborhood of \(z\) (Figure 1). Since we can choose \(ε\) as small as we please, it follows that the points \(z_n\) become arbitrarily close to \(z\) as their subscripts increase. Note that the value of \(n_0\) that is needed will, in general, depend on the value of \(ε\).

Figure 1: Geometric interpretation.

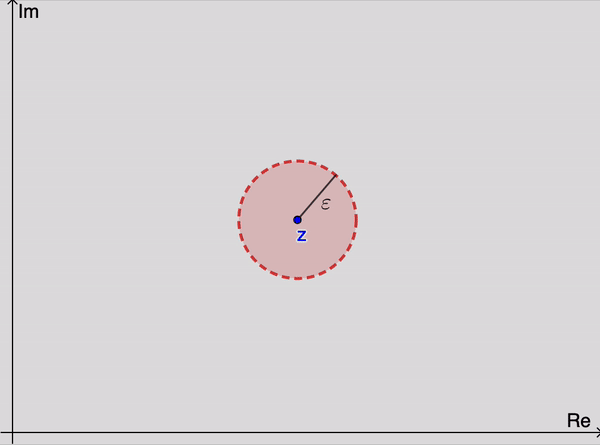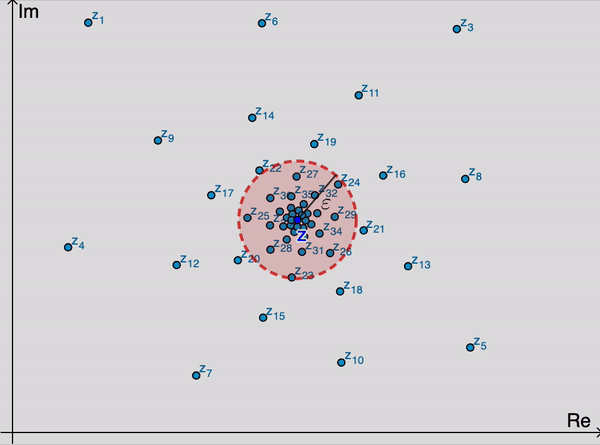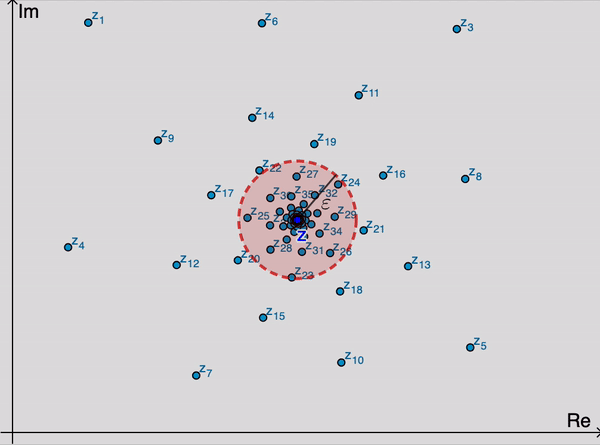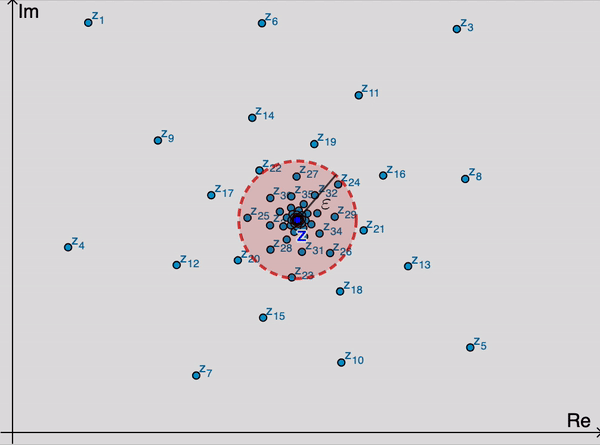
The sequence \(\left\{z_n\right\}_{n=1}^{\infty}\) can have at most one limit. That is, a limit \(z\) is unique if it exists. When that limit exists, the sequence is said to converge to \(z\); and we write

\(\begin{eqnarray*}
            \lim_{n\rightarrow \infty} z_n=z
            \end{eqnarray*}\)

If the sequence has no limit, it diverges.

Theorem \(\PageIndex{1}\)

Suppose that  \(z_n=x_n+iy_n\left ( n=1,2,3,\ldots ​\right )\) and  \(z=x+iy\) . Then

\(\begin{eqnarray}\label{teoseq01}
                    \lim_{n\rightarrow \infty} z_n=z
                    \end{eqnarray}\)

if and only if

\(\begin{eqnarray}\label{teoseq02}
                    \lim_{n\rightarrow \infty} x_n=x\quad \text{and}\quad \lim_{n\rightarrow \infty} y_n=y.
                    \end{eqnarray}\)

Proof

To prove this theorem, we first assume that conditions (3) hold. That is, there exist, for each \(ε>0\), positive integers \(n_1\) and \(n_2\) such that

\(|x_n-x|<\frac{\varepsilon}{2}\quad \text{whenever} \quad n>n_1\)

and

\(|y_n-y|<\frac{\varepsilon}{2}\quad \text{whenever} \quad n>n_2.\)

Hence if \(n_0\) is the larger of the two integers \(n_1\) and \(n_2\),

\(|x_n-x|<\frac{\varepsilon}{2}\quad \text{and} \quad |y_n-y|<\frac{\varepsilon}{2} \quad
                    \text{whenever} \quad n > n_0.\)

Since

\(|(x_n+iy_n)-(x+iy)|=|(x_n-x)+(y_n-y)|\leq |x_n-x|+|y_n-y|,\)

then

\(|z_n-z|< \frac{\varepsilon}{2}+\frac{\varepsilon}{2} \quad \text{whenever} \quad n > n_0.\)

Therefore condition (2) holds.

Conversely, if we start with condition (2), we know that for each positive number \(\varepsilon\), there exists a positive integer \(n_0\) such that

\(|(x_n+iy_n)-(x+iy)|<\varepsilon \quad \text{whenever} \quad n>n_0.\)

However

\(|x_n-x|\leq |(x_n-x)+(y_n-y)|=|(x_n+iy_n)-(x+iy)|\)

and

\(|y_n-y|\leq |(x_n-x)+(y_n-y)|=|(x_n+iy_n)-(x+iy)|.\)

Consequently

\(|x_n-x|<\varepsilon \quad \text{and} \quad |y_n-y|<\varepsilon \quad \text{whenever} \quad n
                    > n_0.\)

Therefore, conditions (3) are satisfied. ■

---

Convergence of Series

An infinite series

\(\begin{eqnarray}\label{series01}
                \sum_{n=1}^{\infty}z_n=z_1+z_2+z_3+\cdots
                \end{eqnarray}\)

of complex numbers converges to the sum \(S\) if the sequence

\(\begin{eqnarray}\label{partialsum}
                \sum_{n=1}^{N}z_n=z_1+z_2+z_3+\cdots +z_N\quad(N=1,2,3,\ldots)
                \end{eqnarray}\)

of partial sums converges to \(S\); we then write

\(\sum_{n=1}^{\infty}z_n=S.\)

Note that since a sequence can have at most one limit, a series can have at most one sum. When a series does not converge, we say that it diverges.

Theorem \(\PageIndex{2}\)

Suppose that \(z_n=x_n+iy_n\left ( n=1,2,3,\ldots ​\right )\) and \(S=X+iY\). Then

\(\begin{eqnarray}\label{teo01}
                    \sum_{n=1}^{\infty} z_n=S
                    \end{eqnarray}\)

if and only if

\(\begin{eqnarray}\label{teo02}
                    \sum_{n=1}^{\infty} x_n=X\quad \text{and}\quad \sum_{n=1}^{\infty} y_n=Y.
                    \end{eqnarray}\)

Proof

To prove this theorem, we first write the partial sums (5) as

\(\begin{eqnarray}\label{teo03}
                    S_N = X_N+iY_N,
                    \end{eqnarray}\)

where

\(X_N = \sum_{n=1}^{N}x_n \quad \text{and}\quad Y_N = \sum_{n=1}^{N}y_n.\)

Now statement (6) is true if and only if

\(\begin{eqnarray}\label{teo04}
                    \lim_{N\rightarrow \infty} S_N = S;
                    \end{eqnarray}\)

and, in view of relation (8) and Theorem 1 on sequences, limit (9) holds if and only if

\(\begin{eqnarray}\label{teo05}
                    \lim_{N\rightarrow \infty} X_N=X\quad \text{and}\quad \lim_{N\rightarrow \infty} Y_N=Y.
                    \end{eqnarray}\)

Limits (10) therefore imply statement (6), and conversely. Since \(X_N=X\) and \(Y_N=Y\) are partial sums of the series (7), the theorem is proved. ■

This theorem can be useful in showing that a number of familiar properties of series in calculus carry over to series whose terms are complex numbers.

Property 1: If a series of complex numbers converges, the \(n\)-th term converges to zero as \(n\) tends to infinity.

It follows from Property 1 that the terms of convergent series are bounded. That is, when series (4) converges, there exists a positive constant \(M\) such that

\(|z_n| \leq M \; \text{ for each positive integer } n.\)

Another important property of series of complex numbers that follows from a corresponding property in calculus is the following.

Property 2: The absolute convergence of a series of complex numbers implies the convergence of that series.

Recall that series (4) is said to be absolutely convergent if the series

\(\begin{eqnarray*}\label{series02}
                \sum_{n=1}^{\infty}|z_n|=\sum_{n=1}^{\infty}\sqrt{x^2_n+y^2_n}\quad \quad(z_n=x_n+iy_n)
                \end{eqnarray*}\)

of real numbers \(\sqrt{x^2_n+y^2_n}\) converges.

To establish the fact that the sum of a series is a given number \(S\), it is often convenient to define the remainder \(ρN\) after \(N\) terms, using the partial sums:

\(\begin{eqnarray*}\label{series03}
            \rho_N=S-S_N
            \end{eqnarray*}\)

Thus \(S=S_N+\rho_N\). Now, since \(|S_N-S|=|\rho_N-0|\), then a series converges to a number \(S\) if and only if the sequence of remainders tends to zero.

Example \(\PageIndex{1}\)

With the aid of remainders, it is easy to verify that

\(\begin{eqnarray*}
                \sum_{n=0}^{\infty}z^n=\frac{1}{1-z}\quad\text{whenever}\quad |z|< 1
                \end{eqnarray*}\)

We need only recall the identity

\(1+z+z^2+\cdots+z^n=\frac{1-z^{n+1}}{1-z}\)

to write the partial sums

\(\begin{eqnarray}
                S_N(z)=\sum_{n=0}^{\infty}z^n=1+z+z^2+\cdots+z^{N-1}\quad\quad(z\neq 1)
                \end{eqnarray}\)

as

\(S_N(z)=\frac{1-z^N}{1-z}.\)

If

\(S(z)=\frac{1}{1-z}\)

then

\(\rho_N(z)=S(z)-S_N(z)=\frac{z^N}{1-z}\quad\quad(z\neq 1).\)

Thus

\(\left|\rho_N\right|=\frac{|z|^N}{|1-z|}\rightarrow 0\quad\text{only when}\quad |z|<1.\)

In this case, it is clear that the remainders \(\rho_N\) tend to zero when \(|z|<1\) but not when \(|z|\geq 1\)

---

Geometric series exploration

The series introduced in the previous example

\(\begin{eqnarray*}
            \sum_{n=0}^{\infty}z^n=\frac{1}{1-z}\quad\text{whenever}\quad |z|< 1
            \end{eqnarray*}\)

is known as the geometric series.

Use the following applet to explore this series. Drag the point \(z\) around. Observe what happens when it is inside, outside or on the border of the unit circle. Drag the slider to show the partial sum.

Code

Enter the following script in GeoGebra to explore it yourself and make your own version. The symbol # indicates comments.

#Complex number
        
Z = 0.72 + ί * 0.61

#Circle of radius 1

c = Circle((0,0), 1)

#Number of terms of the partial series

n = Slider(0, 250, 1, 1, 150, false, true, false, false)

SetValue(n, 250)

#Define the sequence z^n

S = Join({0 + ί * 0, 1 + ί * 0}, Sequence(Z^j, j, 1, n))

#Define partial sum

SP = Sequence(Sum(S, j), j, 1, n + 2)

#Finally join the points of the partial sum

L = Sequence(Segment(Element(SP, j), Element(SP, j + 1)), j, 1, n + 1)