5.2: Taylor Series

For Real Functions

Let $a\in \mathbb R$ and $f(x)$ be and infinitely differentiable function on an interval $I$ containing $a$. Then the one-dimensional Taylor series of $f$ around $a$ is given by

$f(x)=f(a)+f’(a)(x-a)+\frac{f’’(a)}{2!}(x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+\cdots$

which can be written in the most compact form:

$f(x)=\sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n.$

Recall that, in real analysis, Taylor’s theorem gives an approximation of a $k$-times differentiable function around a given point by a $k$-th order Taylor polynomial.

For example, the best linear approximation for $f(x)$ is

$f(x)\approx f(a)+f′(a)(x−a).$

This linear approximation fits $f(x)$ with a line through $x=a$ that matches the slope of $f$ at $a$.

For a better approximation we can add other terms in the expansion. For instance, the best quadratic approximation is

$f(x)\approx f(a)+f’(a)(x−a)+\frac12 f’’(a)(x−a)^2.$

The following applet shows the partial sums of the Taylor series for a given function. Drag the slider to show more terms of the series. Drag the point a or change the function.

 

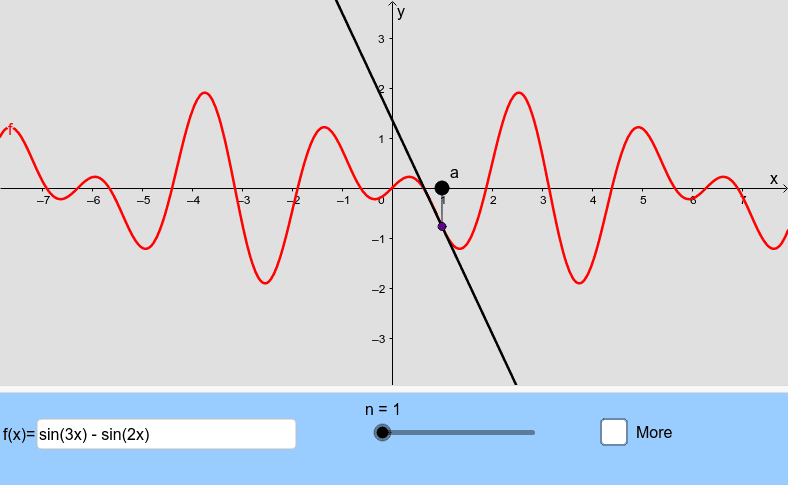
INTERACTIVE GRAPH

 

---

For Complex Functions

Suppose that a function $f$ is analytic throughout a disk $|z -z_0|< R$, centred at $z_0$ and with radius $R_0$. Then $f(z)$ has the power series representation

$\begin{eqnarray}\label{seriefunction}                 f(z)=\sum_{n=0}^{\infty} a_n(z-z_0)^n,\quad |z-z_0|<R,                 \end{eqnarray}$

where

$\begin{eqnarray}                 a_n=\frac{f^{(n)}(z_0)}{n!},\quad n=0,1,2,\ldots                 \end{eqnarray}$

That is, series (1) converges to $f(z)$ when $z$ lies in the stated open disk.

Every complex power series (1) has a radius of convergence. Analogous to the concept of an interval of convergence for real power series, a complex power series (1) has a circle of convergence, which is the circle centered at $z_0$ of largest radius $R>0$ for which (1) converges at every point within the circle $|z−z_0|=R$. A power series converges absolutely at all points $z$ within its circle of convergence, that is, for all $z$ satisfying $|z−z_0|<R$, and diverges at all points $z$ exterior to the circle, that is, for all $z$ satisfying $|z−z_0|>R$. The radius of convergence can be:

1. $R=0$ (in which case (1) converges only at its center $z=z_0$),
2. $R$ a finite positive number (in which case (1) converges at all interior points of the circle $|z−z_0|<R$, or
3. $R=∞$ (in which case (1) converges for all $z$).

The radius of convergence can be calculated using the ratio test of convergece. For example, if:

1. $\displaystyle \lim_{n\rightarrow \infty} \left| \frac{a_{n+1}}{a_n}\right| = L\neq 0$, the radius of convergence is $R=\dfrac{1}{L}$;
2. $\displaystyle \lim_{n\rightarrow \infty}  \left| \frac{a_{n+1}}{a_n}\right|= 0$, the radius of convergence is $R=∞$;
3. $\displaystyle \lim_{n\rightarrow \infty}  \left| \frac{a_{n+1}}{a_n}\right|= \infty$, the radius of convergence is $R=0$.

---

Dynamic Exploration

Use the following applet to explore Taylor series representations and its radius of convergence which depends on the value of $z_0$.

On the left side of the applet below, a phase portrait of a complex function is displayed. On the right side, you can see the approximation of the function through it’s Taylor polynomials at the blue base point $z_0$. The complex function, the base point $z_0$, the order of the polynomial (vertical slider) and the zoom (horizontal slider) can be modified.

 

INTERACTIVE GRAPH

 

 

---

Maclaurin series

A Taylor series with centre $z_0=0$

$f(z) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}z^n$

is referred to as Maclaurin series.

Some important Maclaurin series are:

$\begin{eqnarray*}             \displaystyle \frac{1}{1-z}&=& \sum_{n=0}^{\infty} z^n, \quad |z|\lt 1; \\             \displaystyle e^z &=& \sum_{n=0}^{\infty} \frac{z^n}{n!} \quad |z|\lt \infty;\\             \displaystyle \sin z &=& \sum_{n=0}^{\infty} (-1)^n\frac{z^{2n+1}}{n!} \quad |z|\lt \infty;\\             \displaystyle \cos z &=& \sum_{n=0}^{\infty} (-1)^n \frac{z^{2n}}{n!} \quad |z|\lt \infty;\\             \displaystyle \sinh z &=& \sum_{n=0}^{\infty} \frac{z^{2n+1}}{n!} \quad |z|\lt \infty;\\             \displaystyle \cosh z &=& \sum_{n=0}^{\infty} \frac{z^{2n}}{n!} \quad |z|\lt \infty;             \end{eqnarray*}$

Exercise $\PageIndex{1}$

Exercise: Find the Maclaurin series expansion of the function

$f(z)=\frac{z}{z^4+9}$

and calculate the radius of convergence.

---

Note

The applet was originally written by Aaron Montag using CindyJS. The source can be found at GitHub.