12.1: Principle of the Argument
- Page ID
- 6544
Setup
\(\gamma\) a simple closed curve, oriented in a counterclockwise direction. \(f(z)\) analytic on and inside \(\gamma\), except for (possibly) some finite poles inside (not on) \(\gamma\) and some zeros inside (not on) \(\gamma\).
Let \(p_1, \ ..., p_m\) be the poles of \(f\) inside \(\gamma\).
Let \(z_1, \ ..., z_n\) be the zeros of \(f\) inside \(\gamma\).
Write mult\((z_k)\) = the multiplicity of the zero at \(z_k\). Likewise write mult(\(p_k\)) = the order of the pole at \(p_k\).
We start with a theorem that will lead to the argument principle.
With the above setup
\[\int_{\gamma} \dfrac{f'(z)}{f(z)} \ dz = 2\pi i (\sum \text{mult} (z_k) - \sum \text{mult} (p_k)). \nonumber \]
- Proof
-
To prove this theorem we need to understand the poles and residues of \(f'(z)/f(z)\). With this in mind, suppose \(f(z)\) has a zero of order \(m\) at \(z_0\). The Taylor series for \(f(z)\) near \(z_0\) is
\[f(z) = (z - z_0)^m g(z) \nonumber \]
where \(g(z)\) is analytic and never 0 on a small neighborhood of \(z_0\). This implies
\[\begin{array} {rcl} {\dfrac{f'(z)}{f(z)}} & = & {\dfrac{m(z - z_0)^{m - 1} g(z) + (z - z_0)^m g'(z)}{(z - z_0)^m g(z)}} \\ {} & = & {\dfrac{m}{z - z_0} + \dfrac{g'(z)}{g(z)}} \end{array} \nonumber \]
Since \(g(z)\) is never 0, \(g'(z)/g(z)\) is analytic near \(z_0\). This implies that \(z_0\) is a simple pole of \(f'(z)/f(z)\) and
\[\text{Res} (\dfrac{f'(z)}{f(z)}, z_0) = m \text{mult} (z_0). \nonumber \]
Likewise, if \(z_0\) is a pole of order \(m\) then the Laurent series for \(f(z)\) near \(z_0\) is
\[f(z) = (z - z_0)^{-m} g(z) \nonumber \]
where \(g(z)\) is analytic and never 0 on a small neighborhood of \(z_0\). Thus,
\[\begin{array} {rcl} {\dfrac{f'(z)}{f(z)}} & = & {-\dfrac{m(z - z_0)^{-m - 1} g(z) + (z - z_0)^{-m} g'(z)}{(z - z_0)^{-m} g(z)}} \\ {} & = & {-\dfrac{m}{z - z_0} + \dfrac{g'(z)}{g(z)}} \end{array} \nonumber \]
Again we have that \(z_0\) is a simple pole of \(f'(z)/f(z)\) and
\[\text{Res} (\dfrac{f'(z)}{f(z)}, z_0) = -m = -\text{mult} (z_0). \nonumber \]
The theorem now follows immediately from the Residue Theorem:
\[\begin{array} {rcl} {\int_{\gamma} \dfrac{f'(z)}{f(z)} \ dz} & = & {2\pi i \text{ sum of the residues}} \\ {} & = & {2\pi i (\sum \text{mult} (z_k) - \sum \text{mult} (p_k)).} \end{array} \nonumber \]
We write \(Z_{f, \gamma}\) for the sum of multiplicities of the zeros of \(f\) inside \(\gamma\). Likewise for \(P_{f, \gamma}\). So the Theorem 12.2.1 says,
\[\int_{\gamma} \dfrac{f'}{f} \ dz = 2\pi i (Z_{f, \gamma} - P_{f, \gamma}). \nonumber \]
We have an intuition for what this means. We define it formally via Cauchy’s formula. If \(\gamma\) is a closed curve then its winding number (or index) about \(z_0\) is defined as
\[\text{Ind} (\gamma, z_0) = \dfrac{1}{2\pi i} \int_{\gamma} \dfrac{1}{z - z_0}\ dz. \nonumber \]
Mapping Curves: \(f \circ \gamma\)
One of the key notions in this topic is mapping one curve to another. That is, if \(z = \gamma (t)\) is a curve and \(w = f(z)\) is a function, then \(w = f \circ \gamma (t) = f(\gamma (t))\) is another curve. We say \(f\) maps \(\gamma\) to \(f \circ \gamma\). We have done this frequently in the past, but it is important enough to us now, so that we will stop here and give a few examples. This is a key concept in the argument principle and you should make sure you are very comfortable with it.
Let \(\gamma (t) = e^{it}\) with \(0 \le t \le 2\pi\) (the unit circle). Let \(f(z) = z^2\). Describe the curve \(f \circ \gamma\).
Solution
Clearly \(f \circ \gamma (t) = e^{2it}\) traverses the unit circle twice as \(t\) goes from 0 to \(2\pi\).
Let \(\gamma (t) = it\) with \(-\infty < t < \infty\) (the \(y\)-axis). Let \(f(z) = 1/(z + 1)\). Describe the curve \(f \circ \gamma (t)\).
Solution
\(f(z)\) is a fractional linear transformation and maps the line given by \(\gamma\) to the circle through the origin centered at 1∕2. By checking at a few points:
\(f(-i) = \dfrac{1}{-i + 1} = \dfrac{1 + i}{2}\), \(f(0) = 1\), \(f(i) = \dfrac{1}{i + 1} = \dfrac{1 - i}{2}\), \(f(\infty) = 0\).
We see that the circle is traversed in a clockwise manner as \(t\) goes from \(-\infty\) to \(\infty\).
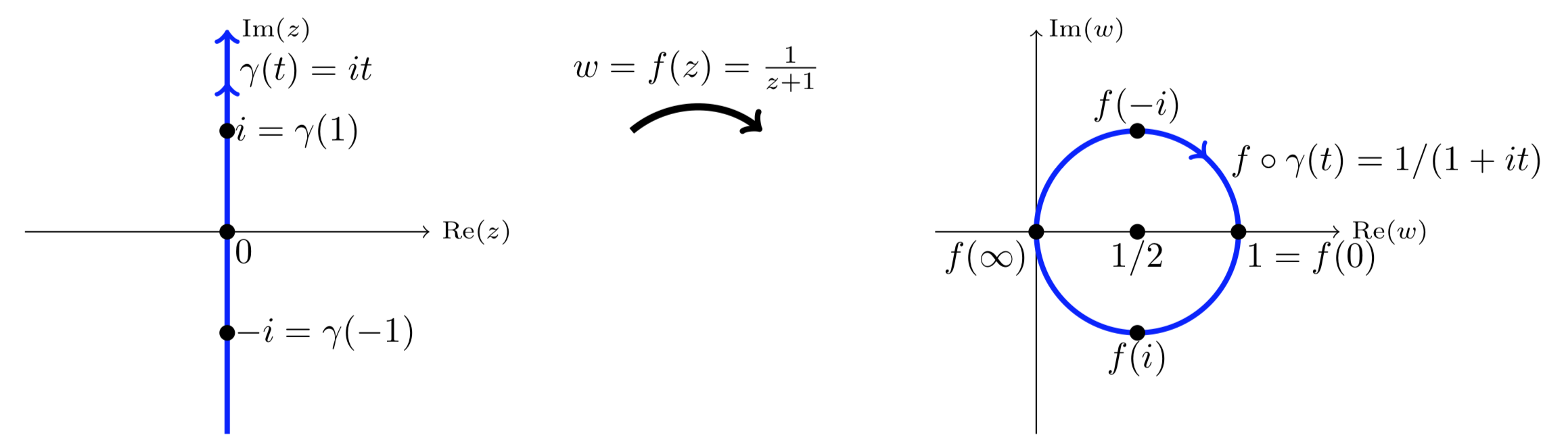
The curve \(z = \gamma (t) = it\) is mapped to \(w = f \circ \gamma (t)) = 1/(it + 1).\)
Argument Principle
You will also see this called the principle of the argument.
For \(f\) and \(\gamma\) with the same setup as above
\[\int_{\gamma} \dfrac{f'(z)}{f(z)}\ dz = 2\pi i \text{Ind} (f \circ \gamma, 0) = 2\pi i (Z_{f, \gamma} - P_{f, \gamma}) \nonumber \]
- Proof
-
Theorem 12.2.1 showed that
\[\int_{\gamma} \dfrac{f'(z)}{f(z)}\ dz = 2\pi i (Z_{f, \gamma} - P_{f, \gamma}) \nonumber \]
So we need to show is that the integral also equals the winding number given. This is simply the change of variables \(w = f(z)\). With this change of variables the countour \(z = \gamma (t)\) becomes \(w = f \circ \gamma (t)\) and \(dw = f'(z)\ dz\) so
\[\int_{\gamma} \dfrac{f'(z)}{f(z)}\ dz = \int_{f \circ \gamma} \dfrac{dw}{w} = 2\pi i \text{Ind} (f \circ \gamma, 0) \nonumber \]
The last equality in the above equation comes from the definition of winding number.
Note that by assumption \(\gamma\) does not go through any zeros of \(f\), so \(w = f(\gamma (t))\) is never zero and \(1/w\) in the integral is not a problem.
Here is an easy corollary to the argument principle that will be useful to us later.
Assume that \(f \circ \gamma\) does not go through −1, i.e. there are no zeros of \(1 + f(z)\) on \(\gamma\) then
\[\int_{\gamma} \dfrac{f'}{f + 1} = 2\pi i \text{Ind}(f \circ \gamma, -1) = 2\pi i (Z_{1 + f, \gamma} - P_{f, \gamma}). \nonumber \]
- Proof
-
Applying the argument principle in Equation 12.2.11 to the function \(1 + f(z)\), we get
\[\int_{\gamma} \dfrac{(1 + f)' f(z)}{1 + f(z)} \ dz = 2\pi i \text{Ind} (1 + f \circ \gamma, 0) = 2\pi i (Z_{1 + f, \gamma} - P_{1 + f, \gamma}) \nonumber \]
Now, we can compare each of the terms in this equation to those in Equation 12.2.14:
\[\begin{array} {rclcl} {\int_{\gamma} \dfrac{(1 + f)' f(z)}{1 + f(z)} \ dz} & = & {\int_{\gamma} \dfrac{f' f(z)}{1 + f(z)} \ dz} & \ \ & {(\text{because } (1 + f)' = f')} \\ {\text{Ind} (1 + f \circ \gamma, 0)} & = & {\text{Ind} (f \circ \gamma, -1)} & \ \ & {(1 + f \text{ winds around 0 } \Leftrightarrow \text{ winds around -1})} \\ {Z_{1 + f, \gamma}} & = & {Z_{1 + f, \gamma}} & \ \ & {(\text{same in both equation}))} \\ {P_{1 + f, \gamma}} & = & {P_{f, \gamma}} & \ \ & {(\text{poles of } f = \text{poles of } 1 + f)} \end{array} \nonumber \]
Let \(f(z) = z^2 + z\) Find the winding number of \(f \circ \gamma\) around 0 for each of the following curves.
- \(\gamma_1\) = circle of radius 2.
- \(\gamma_2\) = circle of radius 1/2.
- \(\gamma_3\) = circle of radius 1.
Solution
\(f(z)\) has zeros at 0, −1. It has no poles.
So, \(f\) has no poles and two zeros inside \(\gamma_1\). The argument principle says \(\text{Ind} (f \circ \gamma_1 , 0) = Z_{f, \gamma_1} - P_{f, \gamma} = 2\)
Likewise \(f\) has no poles and one zero inside \(\gamma_2\), so \(\text{Ind} (f \circ \gamma_2, 0) = 1 - 0 = 1\)
For \(\gamma_3\) a zero of \(f\) is on the curve, i.e. \(f(-1) = 0\), so the argument principle doesn’t apply. The image of \(\gamma_3\) is shown in the figure below – it goes through 0.
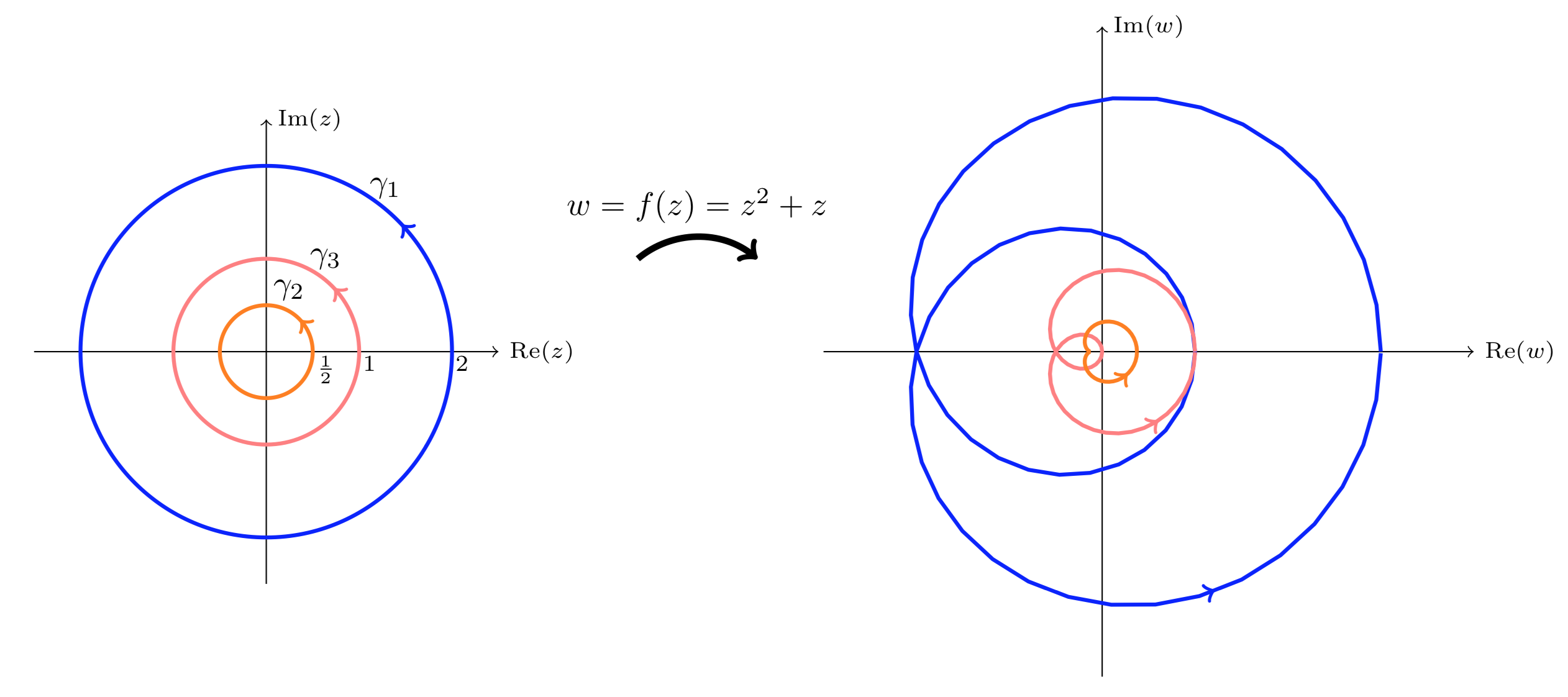
The image of 3 different circles under \(f(z) = z^2 + z\).
Rouché’s Theorem
Make the following assumptions:
- \(\gamma\) is a simple closed curve
- \(f, h\) are analytic functions on and inside \(\gamma\), except for some finite poles.
- There are no poles of \(f\) and \(h\) on \(\gamma\).
- \(|h| < |f|\) everywhere on \(\gamma\).
Then
\[\text{Ind} (f \circ \gamma, 0) = \text{Ind} ((f + h) \circ \gamma, 0). \nonumber \]
That is,
\[Z_{f, \gamma} - P_{f, \gamma} = Z_{f + h, \gamma} - P_{f + h, \gamma} \nonumber \]
- Proof
-
In class we gave a heuristic proof involving a person walking a dog around \(f \circ \gamma\) on a leash of length \(h \circ \gamma\). Here is the analytic proof.
The argument principle requires the function to have no zeros or poles on \(\gamma\). So we first show that this is true of \(f, f + h, (f + h)/f\). The argument is goes as follows.
Zeros: The fact that \(0 \le |h| < |f|\) on \(\gamma\) implies \(f\) has no zeros on \(\gamma\). It also implies \(f + h\) has no zeros on \(\gamma\), since the value of \(h\) is never big enough to cancel that of \(f\). Since \(f\) and \(f + h\) have no zeros, neither does \((f + h)/f\).
Poles: By assumption \(f\) and \(h\) have no poles on \(\gamma\), so \(f + h\) has no poles there. Since \(f\) has no zeors on \(\gamma\), \((f + h)/f\) has no poles there.
Now we can apply the argument principle to \(f\) and \(f + h\)
\[\dfrac{1}{2\pi i} \int_{\gamma} \dfrac{f'}{f} \ dz = \text{Ind} (f \circ \gamma, 0) = Z_{f, \gamma} - P_{f, \gamma}. \nonumber \]
\[\dfrac{1}{2\pi i} \int_{\gamma} \dfrac{(f + h)'}{f + h} \ dz = \text{Ind} ((f + h) \circ \gamma, 0) = Z_{f + h, \gamma} - P_{f + h, \gamma}. \nonumber \]
Next, by assumption \(|\dfrac{h}{f}| < 1\), so \((\dfrac{h}{f}) \circ \gamma\) is inside the unit circle. This means that \(1 + \dfrac{h}{f} = \dfrac{f + h}{f}\) maps \(\gamma\) to the inside of the unit disk centered at 1. (You should draw a figure for this.) This implies that
\[\text{Ind} ((\dfrac{f + h}{f}) \circ \gamma, 0) = 0. \nonumber \]
Let \(g = \dfrac{f + h}{f}\). The above says \(\text{Ind} (g \circ \gamma, 0) = 0\). So, \(\int_{\gamma} \dfrac{g'}{g} \ dz = 0\). (We showed above that \(g\) has no zeros or poles on \(\gamma\).)
Now, it's easy to compute that \(\dfrac{g'}{g} = \dfrac{(f + h)'}{f + h} - \dfrac{f'}{f}\). So, using
\[\text{Ind} (g \circ \gamma, 0) = \int_{\gamma} \dfrac{g'}{g}\ dz = \int_{\gamma} \dfrac{(f + h)'}{f + h} \ dz - \int_{\gamma} \dfrac{f'}{f} \ dz = 0 \Rightarrow \text{Ind} ((f + h) \circ \gamma, 0) = \text{Ind} (f \circ \gamma, 0). \nonumber \]
Now equations 12.2.19 and 12.2.20 tell us \(Z_{f, \gamma} - P_{f, \gamma} = Z_{f + h, \gamma} - P_{f + h, \gamma}\), i.e. we have proved Rouchés theorem.
Under the same hypotheses, If \(h\) and \(f\) are analytic (no poles) then
\[Z_{f, \gamma} = Z_{f + h, \gamma}. \nonumber \]
- Proof
-
Since the functions are analytic \(P_{f, \gamma}\) and \(P_{f + h, \gamma}\) are both 0. So Equation 12.2.18 shows \(Z_f = Z_{f + h}\). \(\text{QED}\)
We think of \(h\) as a small perturbation of \(f\).
Show all 5 zeros of \(z^5 + 3z + 1\) are inside the curve \(C_2: |z| = 2\).
Solution
Let \(f(z) = z^5\) and \(h(z) = 3z + 1\). Clearly all 5 roots of \(f\) (really one root with multiplicity 5) are inside \(C_2\). Also clearly, \(|h| < 7 < 32 = |f|\) on \(C_2\). The corollary to Rouchés theorem says all 5 roots of \(f + h = z^5 + 3z + 1\) must also be inside the curve.
Show \(z + 3 + 2e^z\) has one root in the left half-plane.
Solution
Let \(f(z) = z + 3\), \(h(z) = 2e^z\). Consider the contour from \(-iR\) to \(iR\) along the \(y\)-axis and then the left semicircle of radius \(R\) back to \(-iR\). That is, the contour \(C_1 + C_R\) shown below.
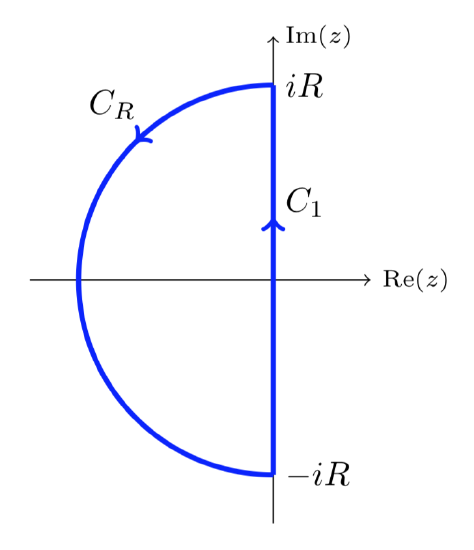
To apply the corollary to Rouchés theorem we need to check that (for \(R\) large) \(|h| < |f|\) on \(C_1 + C_R\). On \(C_1\), \(z = iy\), so
\[|f(z)| = |3 + iy| \ge 3, \ \ \ |h(z)| = 2|e^{iy}| = 2. \nonumber \]
So \(|h| < |f|\) on \(C_1\).
On \(C_R\), \(z = x + iy\) with \(x < 0\) and \(|z| = R\). So,
\[|f(z)| > R - 3 \text{ for } R \text{ large, } |h(z)| = 2|e^{x + iy}| = 2e^x < 2 \text{ (since } x < 0). \nonumber \]
So \(|h| < |f|\) on \(C_R\).
The only zero of \(f\) ia at \(z = -3\), which lies inside the contour.
Therefore, by the Corollary to Rouchés theorem, \(f + h\) has the same number of roots as \(f\) inside the contour, that is 1. Now let \(R\) go to infinity and we see that \(f + h\) has only one root in the entire half-plane.
Rouchés theorem can be used to prove the fundamental theorem of algebra as follows.
- Proof
-
Let
\[P(z) = z^n + a_{n - 1} z^{n - 1} + \ ... + a_0 \nonumber \]
be an \(n\)th order polynomial. Let \(f(z) = z^n\) and \(h = P - f\). Choose an \(R\) such that \(R > \text{max} (1, n |a_{n - 1}|, ..., n|a_0|)\). Then on \(|z| = R\) we have
\[|h| \le |a_{n - 1}| R^{n - 1} + |a_{n - 2}| R^{n - 2} + \ ... + |a_0| \le \dfrac{R}{n} R^{n - 1} + \dfrac{R}{n} R^{n - 2} + \ ... + \dfrac{R}{n} < R^n. \nonumber \]
On \(|z| = R\) we have \(|f(z)| = R^n\), so we have shown \(|h| < |f|\) on the curve. Thus, the corollary to Rouchés theorem says \(f + h\) and \(f\) have the same number of zeros inside \(|z| = R\). Since we know \(f\) has exactly \(n\) zeros inside the curve the same is true for the polynomial \(f + h\). Now let \(R\) go to infinity, we’ve shown that \(f + h\) has exactly \(n\) zeros in the entire plane.
The proof gives a simple bound on the size of the zeros: they are all have magnitude less than or equal to \(\text{max} (1, n |a_{n - 1}|, ..., n|a_0|)\).