4.3: SOME APPLICATIONS OF THE MEAN VALUE THEOREM

In this section, we assume that \(a,b \in \mathbb{R}\) and \(a < b\). In the proposition below, we show that it is possible to use the derivative to determine whether a function is constant. The proof is based on the Mean Value Theorem.

Proposition \(\PageIndex{1}\)

Let \(f\) be continuous on \([a,b]\) and differentiable on \((a,b)\). If \(f^{\prime}(x)=0\) for all \(x \in (a,b)\), then \(f\) is constant on \([a,b]\).

Proof

Suppose by contradiction that \(f\) is not constant on \([a,b]\). Then there exist \(a_{1}\) and \(b_{1}\) such that \(a \leq a_{1}<b_{1} \leq b\) and \(f\left(a_{1}\right) \neq f\left(b_{1}\right)\). By Theorem 4.2.3, there exist \(c \in \left(a_{1}, b_{1}\right)\) such that

\[f^{\prime}(c)=\frac{f\left(b_{1}\right)-f\left(a_{1}\right)}{b_{1}-a_{1}} \neq 0,\]

which is a contradiction. \(\square\)

The next application of the Mean Value Theorem concerns developing simple criteria for monotonicity of real-valued functions based on the derivative.

Proposition \(\PageIndex{2}\)

Let \(f\) be differentiable on \((a,b)\).

1. If \(f^{\prime}(x)>0\) for all \(x \in (a,b)\), then \(f\) is strictly increasing on \((a,b)\).
2. If \(f^{\prime}(x)<0\) for all \(x \in (a,b)\), then \(f\) is strictly decreasing on \((a,b)\).

Proof

Let us prove (i). Fix any \(x_{1}, x_{2} \in(a, b)\) with \(x_{1}<x_{2}\). By Theorem 4.2.3, there exists \(c \in \left(x_{1}, x_{2}\right)\) such that

\[\frac{f\left(x_{2}\right)-f\left(x_{1}\right)}{x_{2}-x_{1}}=f^{\prime}(c)>0.\]

This implies \(f\left(x_{1}\right)<f\left(x_{2}\right)\). Therefore, \(f\) is strictly increasing on \((a,b)\). The proof of (ii) is similar. \(\square\)

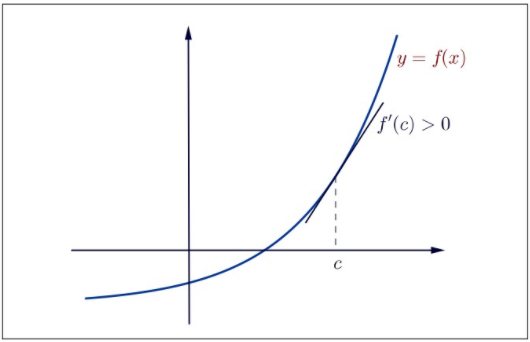
Figure \(4.5\): Strictly Increasing Function.

Example \(\PageIndex{1}\)

Let \(n \in \mathbb{N}\) and \(f:[0, \infty) \rightarrow \mathbb{R}\) be given by \(f(x)=x^{n}\).

Solution

Then \(f^{\prime}(x)=n x^{n-1}\). Therefore, \(f^{\prime}(x) > 0\) for all \(x > 0\) and, so, \(f\) is strictly increasing. In particular, this shows that every positive real number has exactly one \(n\)-th root (refer to Example 3.4.2).

Theorem \(\PageIndex{3}\) - Inverse Function Theorem.

Suppose \(f\) is differentiable on \(I = (a,b)\) and \(f^{\prime}(x) \neq 0\) for all \(x \in (a,b)\). Then \(f\) is one-to-one, \(f(I)\) is an open interval, and the inverse function \(f^{-1}: f(I) \rightarrow I\) is differentiable. Moreover,

\[\left(f^{-1}\right)^{\prime}(y)=\frac{1}{f^{\prime}(x)},\]

where \(f(x) = y\).

Proof

It follows from Theorem 4.2.5 that

\[f^{\prime}(x)>0 \text { for all } x \in (a,b), \text { or } f^{\prime}(x)<0 \text { for all } x \in (a,b).\]

Suppose \(f^{\prime}(x)>0\) for all \(x \in (a,b)\). Then \(f\) is strictly increasing on this interval and, hence, it is one-to-one. It follows from Theorem 3.4.10 and Remark 3.4.11 that \(f(I)\) is an open interval and \(f^{-1}\) is continuous on \(f(I)\).

It remains to prove the differentiability of the inverse function \(f^{-1}\) and the representation of its derivative (4.7). Fix any \(\bar{y} \in f(I)\) with \(\bar{y} = f(\bar{x})\). Let \(g=f^{-1}\). We will show that

\[\lim _{y \rightarrow \bar{y}} \frac{g(y)-g(\bar{y})}{y-\bar{y}}=\frac{1}{f^{\prime}(\bar{x})}.\]

Fix any sequence \(\left\{y_{k}\right\}\) in \(f(I)\) that converges to \(\bar{y}\) and \(y_{k} \neq \bar{y}\) for every \(k\). For each \(y_{k}\), there exists \(x_{k} \in I\) such that \(f\left(x_{k}\right)=y_{k}\). That is, \(g\left(y_{k}\right)=x_{k}\) for all \(k\). It follows from the continuity of \(g\) that \(\left\{x_{k}\right\}\) converges to \(\bar{x}\). Then

\[\begin{aligned}
\lim _{k \rightarrow \infty} \frac{g\left(y_{k}\right)-g(\bar{y})}{y_{k}-\bar{y}} &=\lim _{k \rightarrow \infty} \frac{x_{k}-\bar{x}}{f\left(x_{k}\right)-f(\bar{x})} \\
&=\lim _{k \rightarrow \infty} \frac{1}{\frac{f\left(x_{k}\right)-f(\bar{x})}{x_{k}-\bar{x}}}=\frac{1}{f^{\prime}(\bar{x})}
\end{aligned}.\]

The proof is now complete. \(\square\)

Example \(\PageIndex{2}\)

Let \(n \in \mathbb{N}\) and consider the function \(f:(0, \infty) \rightarrow \mathbb{R}\) given by \(f(x)=x^{n}\).

Solution

Then \(f\) is differentiable and \(f^{\prime}(x)=n x^{n-1} \neq 0\) for all \(x \in(0, \infty)\). It is also clear that \(f((0, \infty))=(0, \infty)\). It follows from the Inverse Function Theorem that \(f^{-1}:(0, \infty) \rightarrow(0, \infty)\) is differentiable and given \(y \in(0, \infty)\)

\[\left(f^{-1}\right)^{\prime}(y)=\frac{1}{f^{\prime}\left(f^{-1}(y)\right)}=\frac{1}{n\left(f^{-1}(y)\right)^{n-1}}.\]

Given \(y > 0\), the value \(f^{-1}(y)\) is the unique positive real number whose \(n\)-th power is \(y\). We call \(f^{-1}(y)\) the (positive) \(n\)-th root of \(y\) and denote it by \(\sqrt[n]{y}\). We also obtain the formula

\[\left(f^{-1}\right)^{\prime}(y)=\frac{1}{n(\sqrt[n]{y})^{n-1}}.\]

Exercise \(\PageIndex{1}\)

1. Let \(f: \mathbb{R} \rightarrow \mathbb{R}\) be differentiable. Prove that if \(f^{\prime}(x)\) is bounded, then \(f\) is Lipschitz continuous and, in particular, uniformly continuous.
2. Give an example of a function \(f:(0, \infty) \rightarrow \mathbb{R}\) which is differentiable and uniformly continuous but such that \(f^{\prime}(x)\) is not bounded.

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{2}\)

Let \(f: \mathbb{R} \rightarrow \mathbb{R}\). Suppose there exist \(\ell \geq 0\) and \(\alpha > 0\) such that

\[|f(u)-f(v)| \leq \ell|u-v|^{\alpha} \text { for all } u, v \in \mathbb{R}\].

1. Prove that \(f\) is uniformly continuous on \(\mathbb{R}\).
2. Prove that if \(\alpha > 1\), then \(f\) is a constant function.
3. Find a nondifferentiable function that satisfies the condition above for \(\alpha = 1\).

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{3}\)

Let \(f\) and \(g\) be differentiable functions on \(\mathbb{R}\) such that \(f\left(x_{0}\right)=g\left(x_{0}\right)\) and

\[f^{\prime}(x) \leq g^{\prime}(x) \text { for all } x \geq x_{0}.\]

Prove that

\[f(x) \leq g(x) \text { for all } x \geq x_{0}.\]

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{4}\)

Let \(f, g: \mathbb{R} \rightarrow \mathbb{R}\) be differentiable functions satisfying

1. \(f(0)=g(0)=1\)
2. \(f(x)>0, g(x)>0\) and \(\frac{f^{\prime}(x)}{f(x)}>\frac{g^{\prime}(x)}{g(x)}\) for all \(x\).

Prove that

\[\frac{f(1)}{g(1)}>1>\frac{g(1)}{f(1)}.\]

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{5}\)

Let \(f\) be twice differentiable on an open interval \(I\). Suppose that there exist \(a,b,c \in I\) with \(a < b < c\) such that \(f(a)<f(b)\) and \(f(b)>f(c)\). Prove that exist \(d \in(a, c)\) such that \(f^{\prime \prime}(d)<0\).

Answer

Add texts here. Do not delete this text first.

Exercise \(\PageIndex{6}\)

Prove that the function \(f\) defined in Exercise 4.1.11 is not monotone on any open interval containing \(0\).

Answer

Add texts here. Do not delete this text first.