8.4: Integration of Elementary Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
In Chapter 5, integration was treated as antidifferentiation. Now we adopt another, measure-theoretical approach.
Lebesgue's original theory was based on Lebesgue measure (Chapter 7, §8). The more general modern treatment develops the integral for functions f:S→E in an arbitrary measure space. Henceforth, (S,M,m) is fixed, and the range space E is E1,E∗,C,En, or another complete normed space. Recall that in such a space, ∑i|ai|<∞ implies that ∑ai converges and is permutable (Chapter 7, §2).
We start with elementary maps, including simple maps as a special case.
Let f:S→E be elementary on A∈M; so f=ai on Ai for some M-partition
A=⋃iAi (disjoint).
(Note that there may be many such partitions.)
We say that f is integrable (with respect to m), or m-integrable, on A iff
∑|ai|mAi<∞.
(The notation "|ai|mAi" always makes sense by our conventions (2*) in Chapter 4, §4.) If m is Lebesgue measure, then we say that f is Lebesgue integrable, or L-integrable.
We then define ∫Af, the m-integral of f on A, by
∫Af=∫Afdm=∑iaimAi.
(The notation "dm" is used to specify the measure m.)
The "classical" notation for ∫Afdm is ∫Af(x)dm(x).
Note 1. The assumption
∑|ai|mAi<∞
implies
(∀i)|ai|mAi<∞;
so ai=0 if mAi=∞, and mAi=0 if |ai|=∞. Thus by our conventions, all "bad" terms aimAi vanish. Hence the sum in (1) makes sense and is finite.
Note 2. This sum is also independent of the particular choice of {Ai}. For if {Bk} is another M-partition of A, with f=bk on Bk, say, then f=ai=bk on Ai∩Bk whenever Ai∩Bk≠∅. Also,
(∀i)Ai=⋃k(Ai∩Bk) (disjoint);
so
(∀i)aimAi=∑kaim(Ai∩Bk),
and hence (see Theorem 2 of Chapter 7, §2, and Problem 11 there)
∑iaimAi=∑i∑kaim(Ai∩Bk)=∑k∑ibkm(Ai∩Bk)=∑kbkmBk.
(Explain!)
This makes our definition (1) unambiguous and allows us to choose any M-partition {Ai}, with f constant on each Ai, when forming integrals (1).
Let f:S→E be elementary and integrable on A∈M. Then the following statements are true.
(i) |f|<∞ a.e. on A.
(ii) f and |f| are elementary and integrable on any M-set B⊆A, and
|∫Bf|≤∫B|f|≤∫A|f|.
(iii) The set B=A(f≠0) is σ-finite (Definition 4 in Chapter 7, §5), and
∫Af=∫Bf.
(iv) If f=a (constant) on A,
∫Af=a⋅mA.
(v) ∫A|f|=0 iff f=0 a.e. on A.
(vi) If mQ=0, then
∫Af=∫A−Qf
(so we may neglect sets of measure 0 in integrals).
(vii) For any k in the scalar field of E,kf is elementary and integrable, and
∫Akf=k∫Af.
Note that if f is scalar valued, k may be a vector. If E=E∗, we assume k∈E1.
- Proof
-
(i) By Note 1, |f|=|ai|=∞ only on those Ai with mAi=0. Let Q be the union of all such Ai. Then mQ=0 and |f|<∞ on A−Q, proving (i).
(ii) If {Ai} is an M-partition of A,{B∩Ai} is one for B. (Verify!) We have f=ai and |f|=|ai| on B∩Ai⊆Ai.
Also,
∑|ai|m(B∩Ai)≤∑|ai|mAi<∞.
(Why?) Thus f and |f| are elementary and integrable on B, and (ii) easily follows by formula (1).
(iii) By Note 1, f=0 on Ai if mAi=∞. Thus f≠0 on Ai only if mAi<∞. Let {Aik} be the subsequence of those Ai on which f≠0; so
(∀k)mAik<∞.
Also,
B=A(f≠0)=⋃kAik∈M (σ-finite!).
By (ii), f is elementary and integrable on B. Also,
∫Bf=∑kaikmAik,
while
∫Af=∑iaimAi.
These sums differ only by terms with ai=0. Thus (iii) follows.
The proof of (iv)-(vii) is left to the reader.◻
Note 3. If f:S→E∗ is elementary and sign-constant on A, we also allow that
∫Af=∑iaimAi=±∞.
Thus here ∫Af exists even if f is not integrable. Apart from claims of integrability and σ-finiteness, Corollary 1(ii)-(vii) hold for such f, with the same proofs.
Let m be Lebesgue measure in E1. Define f=1 on R (rationals) and f=0 on E1−R; see Chapter 4, §1, Example (c). Let A=[0,1].
By Corollary 1 in Chapter 7, §8, A∩R∈M∗ and m(A∩R)=0. Also, A−R∈M∗.
Thus {A∩R,A−R} is an M∗-partition of A, with f=1 on A∩R and f=0 on A−R.
Hence f is elementary and integrable on A, and
∫Af=1⋅m(A∩R)+0⋅m(A−R)=0.
Thus f is L-integrable (even though it is nowhere continuous).
(i) If f:S→E is elementary and integrable or elementary and nonnegative on A∈M, then
∫Af=∑k∫Bkf
for any M-partition {Bk} of A.
(ii) If f is elementary and integrable on each set Bk of a finite M-partition
A=⋃kBk,
it is elementary and integrable on all of A, and (2) holds again.
- Proof
-
(i) If f is elementary and integrable or elementary and nonnegative on A=⋃kBk, it is surely so on each Bk by Corollary 2 of §1 and Corollary 1(ii) above.
Thus for each k, we can fix an M-partition Bk=⋃iAki, with f constant (f=aki) on Aki,i=1,2,…. Then
A=⋃kBk=⋃k⋃iAki
is an M-partition of A into the disjoint sets Aki∈M.
Now, by definition,
∫Bkf=∑iakimAki
and
∫Af=∑k,iakimAki=∑k(∑iakimAki)=∑k∫Bkf
by rules for double series. This proves formula (2).
(ii) If f is elementary and integrable on Bk(k=1,…,n), then with the same notation, we have
∑i|aki|mAki<∞
(by integrability); hence
n∑k=1∑i|aki|mAki<∞.
This means, however, that f is elementary and integrable on A, and so clause (ii) follows.◻
Caution. Clause (ii) fails if the partition {Bk} is infinite.
(i) If f,g:S→E∗ are elementary and nonnegative on A, then
∫A(f+g)=∫Af+∫Ag.
(ii) If f,g:S→E are elementary and integrable on A, so is f±g, and
∫A(f±g)=∫Af±∫Ag.
- Proof
-
Arguing as in the proof of Theorem 1 of §1, we can make f and g constant on sets of one and the same M-partition of A, say, f=ai and g=bi on Ai∈M; so
f±g=ai±bi on Ai,i=1,2,….
In case (i), f,g≥0; so integrability is irrelevant by Note 3, and formula (1) yields
∫A(f+g)=∑i(ai+bi)mAi=∑iaimAi+∑bimAi=∫Af+∫Ag.
In (ii), we similarly obtain
∑i|ai±bi|mAi≤∑|ai|mAi+∑i|bi|mAi<∞.
(Why?) Thus f±g is elementary and integrable on A. As before, we also get
∫A(f±g)=∫Af±∫Ag,
simply by rules for addition of convergent series. (Verify!)◻
Note 4. As we know, the characteristic function CB of a set B⊆S is defined
CB(x)={1,x∈B,0,x∈S−B.
If g:S→E is elementary on A, so that
g=ai on Ai,1,2,…,
for some M-partition
A=⋃Ai,
then
g=∑iaiCAi on A.
(This sum always exists for disjoint sets Ai. Why?) We shall often use this notation.
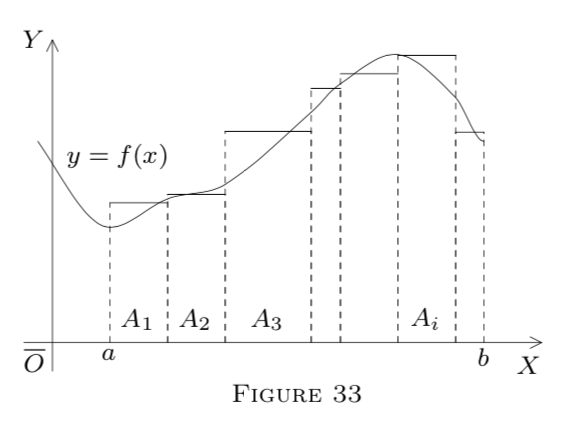
If m is Lebesgue measure in E1, the integral
∫Ag=∑iaimAi
has a simple geometric interpretation; see Figure 33. Let A=[a,b]⊂E1; let g be bounded and nonnegative on E1. Each product aimAi is the area of a rectangle with base Ai and altitude ai. (We assume the Ai to be intervals here.) The total area,
∫Ag=∑iaimAi,
can be treated as an approximation to the area under some curve y=f(x), where f is approximated by g (Theorem 3 in §1). Integration historically arose from such approximations.
Integration of elementary extended-real functions. Note 3 can be extended to sign-changing functions as follows.
If
f=∑iaiCAi(ai∈E∗)
on
A=⋃iAi(Ai∈M),
we set
∫Af=∫Af+−∫Af−,
with
f+=f∨0≥0 and f−=(−f)∨0≥0;
see §2.
By Theorem 2 in §2, f+ and f− are elementary and nonnegative on A; so
∫Af+ and ∫Af−
are defined by Note 3, and so is
∫Af=∫Af+−∫Af−
by our conventions (2*) in Chapter 4, §4.
We shall have use for formula (3), even if
∫Af+=∫Af−=∞;
then we say that ∫Af is unorthodox and equate it to +∞, by convention; cf. Chapter 4, §4. (Other integrals are called orthodox.) Thus for elementary and (extended) real functions, ∫Af is always defined. (We further develop this idea in §5.)
Note 5. With f as above, we clearly have
f+=a+i and f−=a−i on Ai,
where
a+i=max(ai,0) and a−i=max(−ai,0).
Thus
∫Af+=∑a+i⋅mAi and ∫Af−=∑a−i⋅mAi,
so that
∫Af=∫Af+−∫Af−=∑ia+i⋅mAi−∑ia−i⋅mAi.
If ∫Af+<∞ or ∫Af−<∞, we can subtract the two series termwise (Problem 14 of Chapter 4, §13) to obtain
∫Af=∑i(a+i−a−i)mAi=∑iaimAi
for a+i−a−i=ai. Thus formulas (3) and (4) agree with our previous definitions.


