1.4: Inequivalence of Ball and Polydisc

Definition: Biholomorphic

Two domains and are said to be biholomorphic or biholomorphically equivalent if there exists a one-to-one and onto holomorphic map such that the inverse is holomorphic. The mapping is said to be a biholomorphic map or a biholomorphism.

As function theory on two biholomorphic domains is the same, one of the main questions in complex analysis is to classify domains up to biholomorphic transformations. In one variable, there is the rather striking theorem due to Riemann:

Theorem : Riemann Mapping Theorem

If is a nonempty simply connected domain such that , then is biholomorphic to .

In one variable, a topological property on is enough to classify a whole class of domains. It is one of the reasons why studying the disc is so important in one variable, and why many theorems are stated for the disc only. There is simply no such theorem in several variables. We will show momentarily that the unit ball and the polydisc, are not biholomorphically equivalent. Both are simply connected (have no holes), and they are the two most obvious generalizations of the disc to several variables. They are homeomorphic, that is, topology does not see any difference.

Exercise

Prove that there exists a homeomorphism , that is, is a bijection, and both and are continuous.

Let us stick with . Instead of proving that and are biholomorphically inequivalent we will prove a stronger theorem. First a definition.

Definition: Proper Map

Suppose is a continuous map between two topological spaces. Then is a proper map if for every compact , the set is compact.

The notation “” is a common notation for relatively compact subset, that is, the closure is compact in the relative (subspace) topology. Often the distinction between compact and relatively compact is not important. For instance, in the definition above we can replace compact with relatively compact. So the notation is sometimes used if “compact” is meant.

Vaguely, “proper” means that “boundary goes to the boundary.” As a continuous map, pushes compacts to compacts; a proper map is one where the inverse does so too. If the inverse is a continuous function, then clearly is proper, but not every proper map is invertible. For example, the map given by is proper, but not invertible. The codomain of is important. If we replace by , still given by , then the map is no longer proper. Let us state the main result of this section.

Theorem : Rothstein 1935

There exists no proper holomorphic mapping of the unit bidisc to the unit ball .

As a biholomorphic mapping is proper, the unit bidisc is not biholomorphically equivalent to the unit ball in . This fact was first proved by Poincaré by computing the automorphism groups of and , although his proof assumed the maps extended past the boundary. The first complete proof was by Henri Cartan in 1931, though popularly the theorem is attributed to Poincaré. It seems standard practice that any general audience talk about several complex variables contains a mention of Poincaré, and often the reference is to this exact theorem.

We need some lemmas before we get to the proof of the result. First, a certain one-dimensional object plays an important role in the geometry of several complex variables. It allows us to apply one-variable results in several variables. It is especially important in understanding the boundary behavior of holomorphic functions. It also prominently appears in complex geometry.

Definition: Analytic Disc

A nonconstant holomorphic mapping is called an analytic disc. If the mapping extends continuously to the closed unit disc , then the mapping is called a closed analytic disc.

Often we call the image the analytic disc rather than the mapping. For a closed analytic disc we write and call it the boundary of the analytic disc.

In some sense, analytic discs play the role of line segments in . It is important to always have in mind that there is a mapping defining the disc, even if we are more interested in the set. Obviously for a given image, the mapping is not unique.

Let us consider the boundaries of the unit bidisc and the unit ball . We notice the boundary of the unit bidisc contains analytic discs and for . That is, through every point in the boundary, except for the distinguished boundary , there exists an analytic disc lying entirely inside the boundary. On the other hand, the ball contains no analytic discs in its boundary.

Proposition

The unit sphere contains no analytic discs.

Proof

Suppose there is a holomorphic function such that the image is inside the unit sphere. In other words, for all . Without loss of generality (after composing with a unitary matrix) assume that . Consider the first component and notice that . If a sum of positive numbers is less than or equal to 1, then they all are, and hence . Maximum principle says that for all . But then for all and all . Therefore, is constant and thus not an analytic disc.

The fact that the sphere contains no analytic discs is the most important geometric distinction between the boundary of the polydisc and the sphere.

Exercise

Modify the proof to show some stronger results.

1. Let be an analytic disc and . Prove contains points not in .
2. Let be an analytic disc. Prove that is nowhere dense in .
3. Find an analytic disc in , such that , , and locally near , the set is the curve defined by , , .

Before we prove the theorem, let us prove a lemma making the statement about proper maps taking boundary to boundary precise.

Lemma

Let and be bounded domains and let be continuous. Then is proper if and only if for every sequence in such that , the set of limit points of lies in .

Proof

Suppose is proper. Take a sequence in such that . Then take any convergent subsequence of converging to some . Consider as a set. Let be the closure of in (subspace topology). If , then and is compact. Otherwise, if , then . The inverse image is not compact (it contains a sequence going to ) and hence is not compact either as is proper. Thus , and hence . As we took an arbitrary subsequence of , was an arbitrary limit point. Therefore, all limit points are in .

Let us prove the converse. Suppose that for every sequence in such that , the set of limit points of lies in . Take a closed set (subspace topology) and look at . If is not compact, then there exists a sequence in such that . That is because is closed (in ) but not compact. The hypothesis then says that the limit points of are in . Hence has limit points in and is not compact.

Exercise

Let and be bounded domains and let be continuous. Suppose , and is defined by for all . Prove that is proper if and only if .

Exercise

Let be a continuous function of locally compact Hausdorff topological spaces. Let and be the one-point compactifications of and . Then is a proper map if and only if it extends as a continuous map by letting and .

We now have all the lemmas needed to prove the theorem of Rothstein.

Proof of Theorem . Suppose there is a proper holomorphic map . Fix some in the boundary of the disc . Take a sequence such that . The functions map the unit disc into . By the standard Montel’s theorem, by passing to a subsequence we assume that the sequence of functions converges (uniformly on compact subsets) to a limit . As , then by Lemma we have that and hence must be constant.

Let denote the derivative (we differentiate each component). The functions converge to . So for an arbitrary fixed , . This limit holds for all and some subsequence of an arbitrary sequence where . The holomorphic mapping , therefore, extends continuously to the closure and is zero on . We apply the maximum principle or the Cauchy formula and the fact that was arbitrary to find . By symmetry . Therefore, is constant, which is a contradiction as was proper.

The proof is illustrated in Figure .

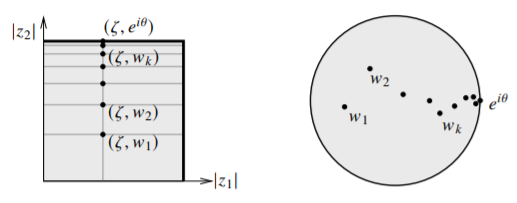
Figure

In the picture, on the left-hand side is the bidisc, and we restrict to the horizontal gray lines (where the second component is fixed to be ) and take a limit to produce an analytic disc in the boundary of . We then show that on the vertical gray line (where the first component is fixed to be ). The right-hand side shows the disc where is fixed, which corresponds to the vertical gray line on the left.

The proof says that the reason why there is not even a proper mapping is the fact that the boundary of the polydisc contains analytic discs, while the sphere does not. The proof extends easily to higher dimensions as well, and the proof of the generalization is left as an exercise.

Theorem

Let , , and , , be bounded domains such that contains no analytic discs. Then there exist no proper holomorphic mapping .

Exercise

Prove Theorem

The key takeaway from this section is that in several variables, to see if two domains are equivalent, the geometry of the boundaries makes a difference, not just the topology of the domains.

The following is a fun exercise in one dimension about proper maps of discs:

Exercise

Let be a proper holomorphic map. Then for some real and some (that is, is a finite Blaschke product). Hint: Consider .

In several variables, when is replaced by a ball, this question (what are the proper maps) becomes far more involved, and if the dimensions of the balls are different, it is not solved in general.

Exercise

Suppose be a proper holomorphic map where is a nonempty domain. Prove that . Hint: Consider the same idea as in Exercise 1.2.19.

Exercise

Suppose is a nonconstant continuous map such that is holomorphic and whenever . Prove that maps into and furthermore that this map is proper.