2.6: Holomorphic Convexity

Definition: Holomorphic Hull

Let \(U \subset \mathbb{C}^n\) be a domain. For a set \(K \subset U\), define the holomorphic hull \[\widehat{K}_U \overset{\text{def}}{=} \Bigl\{ z \in U : |f(z)| \leq \sup_{w\in K} |f(w)| \text{ for all $f \in \mathcal{O}(U)$} \Bigr\} .\] A domain \(U\) is holomorphically convex if whenever \(K \subset \subset U\), then \(\widehat{K}_U \subset \subset U\). In other words, \(U\) is holomorphically convex if it is convex with respect to moduli of holomorphic functions on \(U\).\(^{1}\)

It is a simple exercise (see below) to show that a holomorphically convex domain is Hartogs pseudoconvex. We will prove that holomorphic convexity is equivalent to being a domain of holomorphy. That a Hartogs pseudoconvex domain is holomorphically convex is the Levi problem for Hartogs pseudoconvex domains and is considerably more difficult. The thing is, there are lots of plurisubharmonic functions, and they are easy to construct; we can even construct them locally, and then piece them together by taking maxima. There are far fewer holomorphic functions, and we cannot just construct them locally and expect the pieces to somehow fit together. As it is so fundamental, let us state it as a theorem.

Theorem \(\PageIndex{1}\): Solution of the Levi Problem

A domain \(U \subset \mathbb{C}^n\) is holomorphically convex if and only it is Hartogs pseudoconvex.

Proof

The forward direction follows from an exercise below. We skip the proof of the backward direction in order to save some hundred pages or so. See Hörmander’s book [H] for the proof.

Exercise \(\PageIndex{1}\)

Prove that a holomorphically convex domain is Hartogs pseudoconvex. See Exercise 2.4.22.

Exercise \(\PageIndex{2}\)

Prove that every domain \(U \subset \mathbb{C}\) is holomorphically convex by giving a topological description of \(\widehat{K}_U\) for any compact \(K \subset \subset U\). Hint: Runge may be useful.

Exercise \(\PageIndex{3}\)

Suppose \(f \colon \mathbb{C}^n \to \mathbb{C}\) is holomorphic and \(U\) is a topological component of \(\bigl\{ z \in \mathbb{C}^n : |f(z)| < 1 \bigr\}\). Prove that \(U\) is a holomorphically convex domain.

Exercise \(\PageIndex{4}\)

Compute the hull \(\widehat{K}_{\mathbb{D}^n}\) of the set \(K = \bigl\{ z \in \mathbb{D}^n : |z_j| = \lambda_j \text{ for } j=1,\ldots,n \bigr\}\), where \(0 \leq \lambda_j < 1\). Prove that the unit polydisc is holomorphically convex.

Exercise \(\PageIndex{5}\)

Prove that a geometrically convex domain \(U \subset \mathbb{C}^n\) is holomorphically convex.

Exercise \(\PageIndex{6}\)

Prove that the Hartogs figure (see Theorem 2.1.1) is not holomorphically convex.

Exercise \(\PageIndex{7}\)

Let \(U \subset \mathbb{C}^n\) be a domain, \(f \in \mathcal{O}(U)\), and \(f\) is not identically zero. Show that if \(U\) is holomorphically convex, then \(\widetilde{U} = \bigl\{ z \in U : f(z) \not= 0 \bigr\}\) is holomorphically convex. Hint: First see Exercise 1.6.2.

Exercise \(\PageIndex{8}\)

Suppose \(U,V \subset \mathbb{C}^n\) are biholomorphic domains. Prove that \(U\) is holomorphically convex if and only if \(V\) is holomorphically convex.

Exercise \(\PageIndex{9}\)

In the definition of holomorphic hull of \(K\), replace \(U\) with \(\mathbb{C}^n\) and \(\mathcal{O}(U)\) with holomorphic polynomials on \(\mathbb{C}^n\), to get the polynomial hull of \(K\). Prove that the polynomial hull of \(K \subset \subset \mathbb{C}^n\) is the same as the holomorphic hull \(\widehat{K}_{\mathbb{C}^n}\).

Exercise \(\PageIndex{10}\)

1. Prove the Hartogs triangle \(T\) (see Exercise 2.1.7) is holomorphically convex.
2. Prove \(T \cup B_{\epsilon}(0)\) (for a small enough \(\epsilon > 0\)) is not holomorphically convex.

Exercise \(\PageIndex{11}\)

Show that if domains \(U_1 \subset \mathbb{C}^n\) and \(U_2 \subset \mathbb{C}^n\) are holomorphically convex, then so are all the topological components of \(U_1 \cap U_2\).

Exercise \(\PageIndex{12}\)

Let \(n \geq 2\).

1. Let \(U \subset \mathbb{C}^n\) be a domain and \(K \subset \subset U\) a nonempty compact subset. Show that \(U \setminus K\) is not holomorphically convex.
2. Let \(U \subset \mathbb{C}^n\) be a bounded holomorphically convex domain. Prove that \(\mathbb{C}^n \setminus U\) is connected.
3. Find an unbounded holomorphically convex domain \(U \subset \mathbb{C}^n\) where \(\mathbb{C}^n \setminus U\) is disconnected.

The set \(\mathbb{C}^n\) is both holomorphically convex and a domain of holomorphy. These two notions are equivalent also for all other domains in \(\mathbb{C}^n\).

Theorem \(\PageIndex{2}\)

Cartan-Thullen

Let \(U \subsetneq \mathbb{C}^n\) be a domain. The following are equivalent:

1. \(U\) is a domain of holomorphy.
2. For all \(K \subset \subset U\), \(\operatorname{dist}(K,\partial U) = \operatorname{dist}(\widehat{K}_U,\partial U)\).
3. \(U\) is holomorphically convex.

Proof

Let us start with (i) \(\Rightarrow\) (iii). Suppose there is a \(K \subset \subset U\) with \(\operatorname{dist}(K,\partial U) > \operatorname{dist}(\widehat{K}_U,\partial U)\). After possibly a rotation by a unitary, there exists a point \(p \in \widehat{K}_U\) and a polydisc \(\Delta = \Delta_r(0)\) with polyradius \(r = (r_1,\ldots,r_n)\) such that \(p + \Delta = \Delta_r(p)\) contains a point of \(\partial U\), but \[K + \Delta = \bigcup_{q \in K} \Delta_r(q) \subset \subset U.\] See Figure \(\PageIndex{1}\).

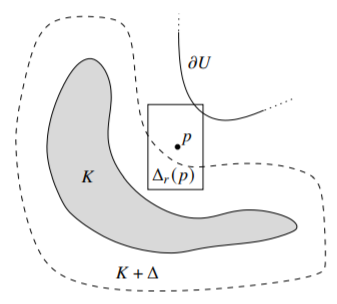
Figure \(\PageIndex{1}\)

If \(f \in \mathcal{O}(U)\), then there is an \(M > 0\) such that \(|f| \leq M\) on \(K + \Delta\) as that is a relatively compact set. By the Cauchy estimates for each \(q \in K\) we get \[\left|\frac{\partial^\alpha f}{\partial z^\alpha}(q)\right| \leq \frac{M \alpha!}{r^\alpha} .\] This inequality therefore holds on \(\widehat{K}_U\) and hence at \(p\). The series \[\sum_{\alpha} \frac{1}{\alpha !}\frac{\partial^\alpha f}{\partial z^\alpha}(p) {(z-p)}^\alpha\] converges in \(\Delta_r(p)\). Hence \(f\) extends to all of \(\Delta_r(p)\) and \(\Delta_r(p)\) contains points outside of \(U\), in other words, \(U\) is not a domain of holomorphy.

The implication (ii) \(\Rightarrow\) (iii) is immediate.

Finally, we prove (iii) \(\Rightarrow\) (i). Suppose \(U\) is holomorphically convex. Let \(p \in \partial U\). By convexity choose nested compact sets \(K_{j-1} \subsetneq K_j \subset \subset U\) such that \(\bigcup_j K_j = U\), and \(\widehat{(K_j)}_U = K_j\). As the sets exhaust \(U\), we can perhaps pass to a subsequence to ensure that there exists a sequence of points \(p_j \in K_j \setminus K_{j-1}\) such that \(\lim_{j\to\infty} p_j = p\).

As \(p_j\) is not in the hull of \(K_{j-1}\), there is a function \(f_j \in \mathcal{O}(U)\) such that \(|f_j| < 2^{-j}\) on \(K_{j-1}\), but \[|f_j(p_j)| > j + \left| \sum_{k=1}^{j-1} f_k(p_j)\right| .\] Finding such a function is left as an exercise below. For any \(j\), the series \(\sum_{k=1}^\infty f_k(z)\) converges uniformly on \(K_j\) as for all \(k > j\), \(|f_k| < 2^{-k}\) on \(K_j\). As the \(K_j\) exhaust \(U\), the series converges uniformly on compact subsets of \(U\). Consequently, \[f(z) = \sum_{k=1}^\infty f_k(z)\] is a holomorphic function on \(U\). We bound \[|f(p_j)| \geq |f_j(p_j)| - \left| \sum_{k=1}^{j-1} f_k(p_j)\right| - \left| \sum_{k=j+1}^\infty f_k(p_j)\right| \geq j - \sum_{k=j+1}^\infty 2^{-k} \geq j-1 .\] So \(\lim_{j\to\infty} f(p_j) = \infty\). Clearly there cannot be any open \(W \subset \mathbb{C}^n\) containing \(p\) to which \(f\) extends (see definition of domain of holomorphy). As any connected open \(W\) such that \(W \setminus U \not= \emptyset\) must contain a point of \(\partial U\), we are done.

By Exercise \(\PageIndex{8}\), holomorphic convexity is a biholomorphic invariant. Thus, being a domain of holomorphy is also a biholomorphic invariant. This fact is not easy to prove from the definition of a domain of holomorphy, as the biholomorphism is defined only on the interior of our domains.

Holomorphic convexity is an intrinsic notion; it does not require knowing anything about points outside of \(U\). It is a much better way to think about domains of holomorphy. Holomorphic convexity generalizes easily to more complicated complex manifolds\(^{2}\), while the notion of a domain of holomorphy only makes sense for domains in \(\mathbb{C}^n\).

Exercise \(\PageIndex{13}\): Behnke-Stein again

Show that the union \(\bigcup_j U_j\) of a nested sequence of holomorphically convex domains \(U_{j-1} \subset U_j \subset \mathbb{C}^n\) is holomorphically convex.

Exercise \(\PageIndex{14}\)

Prove the existence of the function \(f_j \in \mathcal{O}(U)\) as indicated in the proof of Cartan–Thullen above.

Exercise \(\PageIndex{15}\)

Show that if \(U \subset \mathbb{C}^n\) is holomorphically convex, then there exists a single function \(f \in \mathcal{O}(U)\) that does not extend through any point \(p \in \partial U\).

Exercise \(\PageIndex{16}\)

We know \(U = \mathbb{C}^2 \setminus \{ z \in \mathbb{C}^2 : z_1 = 0 \}\) is a domain of holomorphy. Use part (ii) of the theorem to show that if \(W \subset \mathbb{C}^2\) is a domain of holomorphy and \(U \subset W\), then either \(W=U\) or \(W = \mathbb{C}^2\). Hint: Suppose \(L \subset W\) is a complex line and \(K\) is a circle in \(L\). What is \(\widehat{K}_W\)?

In the following series of exercises, which you should most definitely do in order, you will solve the Levi problem (and more) for complete Reinhardt domains. Recall that a domain \(U\) is a if whenever \((z_1,\ldots,z_n)\) is in \(U\) and \(r_j = |z_j|\), then the entire closed polydisc \(\overline{\Delta_r(0)} \subset U\). We say a complete Reinhardt domain \(U\) is logarithmically convex if there exists a (geometrically) convex \(C \subset \mathbb{R}^n\) such that \(z \in U\) if and only if \((\log |z_1|,\ldots,\log |z_n|) \in C\).

Exercise \(\PageIndex{17}\)

Prove that a logarithmically convex complete Reinhardt domain is the intersection of sets of the form \[\bigl\{ z \in \mathbb{C}^n : \alpha_1 \log |z_1| + \cdots + \alpha_n \log |z_n| < \beta \bigr\} = \bigl\{ z \in \mathbb{C}^n : |z_1|^{\alpha_1} \cdots |z_n|^{\alpha_n} < e^\beta \bigr\} \] for some nonnegative \(\alpha_1,\ldots,\alpha_n\), and \(\beta \in \mathbb{R}\).

Exercise \(\PageIndex{18}\)

Prove that a complete Reinhardt domain that is Hartogs pseudoconvex is logarithmically convex.

Exercise \(\PageIndex{19}\)

For each \(k \in \mathbb{N}_0\), let \(\ell_m^k \in \mathbb{N}_0\) be the smallest nonnegative integer such that \(\ell_m^k \geq k \alpha_m\). Prove that the domain of convergence of the power series \[\sum_{k=0}^\infty e^{-k\beta} z_1^{\ell_1^k} \cdots z_n^{\ell_n^k}\] is precisely \(\bigl\{ z \in \mathbb{C}^n : |z_1|^{\alpha_1} \cdots |z_n|^{\alpha_n} < e^\beta \bigr\}\). Hint: That it diverges outside is easy, what is hard is that it converges inside. Perhaps useful is to notice \(\frac{\ell_m^k}{k}-\alpha_m \leq \frac{1}{k}\), and that if \(z\) is in the set, there is some \(\epsilon > 0\) such that \((1+\epsilon)|z_1|^{\alpha_1} \cdots |z_n|^{\alpha_n} = e^{\beta}\).

Exercise \(\PageIndex{20}\)

Prove that a logarithmically convex Reinhardt domain is holomorphically convex and therefore it is a domain of holomorphy.

Exercise \(\PageIndex{21}\)

Prove that a complete Reinhardt domain is a domain of holomorphy if and only if it is the domain of convergence of some power series at the origin. Hint: There is a function that does not extend past any boundary point of a holomorphically convex domain.

We (you) have proved the following proposition.

Proposition \(\PageIndex{1}\)

Let \(U \subset \mathbb{C}^n\) be a complete Reinhardt domain. Then the following are equivalent:

1. \(U\) is logarithmically convex.
2. \(U\) is a domain of holomorphy.
3. \(U\) is a domain of convergence of some power series at the origin.
4. \(U\) is Hartogs pseudoconvex.

Footnotes

[1] Sometimes simply \(\widehat{K}\) is used, but we use \(\widehat{K}_U\) to emphasize the dependence on \(U\).

[2] Manifolds with complex structure, that is, “manifolds with multiplication by \(i\) on the tangent space.”