10.3: Regular Markov Chains

Last updated
Save as PDF

Page ID: 37932

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

In this section, you will learn to:

Identify Regular Markov Chains, which have an equilibrium or steady state in the long run
Find the long term equilibrium for a Regular Markov Chain.

At the end of Section 10.1, we examined the transition matrix T for Professor Symons walking and biking to work. As we calculated higher and higher powers of T, the matrix started to stabilize, and finally it reached its steady-state or state of equilibrium. When that happened, all the row vectors became the same, and we called one such row vector a fixed probability vector or an equilibrium vector E. Furthermore, we discovered that ET = E.

In this section, we wish to answer the following four questions.

Does every Markov chain reach a state of equilibrium? Is there a way to determine if a Markov chain reaches a state of equilibrium?
Does the product of an equilibrium vector and its transition matrix always equal the equilibrium vector? That is, does ET = E?
Can the equilibrium vector E be found without raising the matrix to higher powers?
Does the long term market share distribution for a Markov chain depend on the initial market share?

Exercise $\PageIndex{1}$

Does every Markov chain reach the state of equilibrium?

Answer

No. Some Markov chains reach a state of equilibrium but some do not. Some Markov chains transitions do not settle down to a fixed or equilibrium pattern. Therefore we’d like to have a way to identify Markov chains that do reach a state of equilibrium.

One type of Markov chains that do reach a state of equilibrium are called regular Markov chains. A Markov chain is said to be a regular Markov chain if some power of its transition matrix T has only positive entries.

To determine if a Markov chain is regular, we examine its transition matrix T and powers, Tⁿ, of the transition matrix. If we find any power $n$ for which Tⁿ has only positive entries (no zero entries), then we know the Markov chain is regular and is guaranteed to reach a state of equilibrium in the long run.

Fortunately, we don’t have to examine too many powers of the transition matrix T to determine if a Markov chain is regular; we use technology, calculators or computers, to do the calculations. There is a theorem that says that if an $n \times n$ transition matrix represents $n$ states, then we need only examine powers T^m up to $m = ( n-1)^2 + 1$.
If some power of the transition matrix T^m is going to have only positive entries, then that will occur for some power $m \leq(n-1)^{2}+1$.

For example, if T is a $3 \times 3$ transition matrix, then

\[m = ( n-1)^2 + 1= ( 3-1)^2 + 1=5 . \nonumber \]

If we examine T, T², T³, T⁴ and T⁵, and find that any of those matrices has only positive entries, then we know T is regular.
If however, T, T², T³, T⁴ and T⁵ all have at least one zero entry and none of them have all positive entries, then we can stop checking. All higher powers of T will also have at least one zero entry, and T will not be regular.

Example $\PageIndex{1}$

Determine whether the following Markov chains are regular.

$\mathrm{A}=\left[\begin{array}{ll}
0 & 1 \\
.4 & .6
\end{array}\right]$
$\mathrm{B}=\left[\begin{array}{ll}
1 & 0 \\
3 & 7
\end{array}\right]$

Solution

a.) The transition matrix A does not have all positive entries. But it is a regular Markov chain because

\[ A^{2}=\left[\begin{array}{ll}
.40 & .60 \\
.24 & .76
\end{array}\right] \nonumber \]

has only positive entries.

b.) The matrix B is not a regular Markov chain because every power of B has an entry 0 in the first row, second column position.

\[\mathrm{B}=\left[\begin{array}{ll}
1 & 0 \\
.3 & .7
\end{array}\right] \quad \text { and } \quad \mathrm{B}^{2}=\left[\begin{array}{cc}
1 & 0 \\
.3 & .7
\end{array}\right]\left[\begin{array}{cc}
1 & 0 \\
.3 & .7
\end{array}\right]=\left[\begin{array}{cc}
1 & 0 \\
.51 & .49
\end{array}\right] \nonumber \]

Since B is a $2 \times 2$ matrix, $m = (2-1)^2+1= 2$. We’ve examined B and B², and discovered that neither has all positive entries. We don’t need to examine any higher powers of B; B is not a regular Markov chain.

In fact, we can show that all 2 by 2 matrices that have a zero in the first row, second column position are not regular. Consider the following matrix M.

\[\begin{array}{l}
\mathrm{M}=\left[\begin{array}{ll}
\mathrm{a} & 0 \\
\mathrm{b} & \mathrm{c}
\end{array}\right] \\
\mathrm{M}^{2}=\left[\begin{array}{ll}
a & 0 \\
b & c
\end{array}\right]\left[\begin{array}{ll}
a & 0 \\
b & c
\end{array}\right]=\left[\begin{array}{ll}
\mathrm{a} \cdot \mathrm{a}+0 \cdot \mathrm{b} & \mathrm{a} \cdot 0+0 \cdot \mathrm{c} \\
\mathrm{b} \cdot \mathrm{a}+\mathrm{c} \cdot \mathrm{b} & \mathrm{b} \cdot 0+\mathrm{c} \cdot \mathrm{c}
\end{array}\right]
\end{array} \nonumber \]

Observe that the first row, second column entry, $a \cdot 0 + 0 \cdot c$, will always be zero, regardless of what power we raise the matrix to.

Exercise $\PageIndex{2}$

Does the product of an equilibrium vector and its transition matrix always equal the equilibrium vector? That is, does ET = E?

Answer

At this point, the reader may have already guessed that the answer is yes if the transition matrix is a regular Markov chain. We try to illustrate with the following example from Section 10.1.

A city is served by two cable TV companies, BestTV and CableCast. Due to their aggressive sales tactics, each year 40% of BestTV customers switch to CableCast; the other 60% of BestTV customers stay with BestTV. On the other hand, 30% of the CableCast customers switch to Best RV and 70% of CableCast customers stay with CableCast.

The transition matrix is given below.

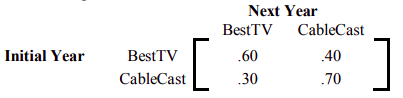
$10.3.2.png$

If the initial market share for BestTV is 20% and for CableCast is 80%, we'd like to know the long term market share for each company.

Let matrix T denote the transition matrix for this Markov chain, and V₀ denote the matrix that represents the initial market share. Then V₀ and T are as follows:

\[\mathrm{V}_{0}=\left[\begin{array}{ll}
.20 & .80
\end{array}\right] \quad \text{ and } \quad \mathrm{T}=\left[\begin{array}{ll}
.60 & .40 \\
.30 & .70
\end{array}\right] \nonumber \]

Since each year people switch according to the transition matrix T, after one year the distribution for each company is as follows:

\[\mathrm{V}_{1}=\mathrm{V}_{0} \mathrm{T}=\left[\begin{array}{ll}
.20 & .80
\end{array}\right]\left[\begin{array}{ll}
.60 & .40 \\
.30 & .70
\end{array}\right]=\left[\begin{array}{ll} .36 & .64 \end{array}\right] \nonumber \]

After two years, the market share for each company is

\[\mathrm{V}_{2}=\mathrm{V}_{1} \mathrm{T}=\left[\begin{array}{lll}
.36 & .64
\end{array}\right]\left[\begin{array}{ll}
.60 & .40 \\
.30 & .70
\end{array}\right]=\left[\begin{array}{ll}
.408 & .592
\end{array}\right] \nonumber \]

After three years the distribution is

\[\mathrm{V}_{3}=\mathrm{V}_{2} \mathrm{T}=\left[\begin{array}{ll}
.408 & .592
\end{array}\right]\left[\begin{array}{ll}
.60 & .40 \\
.30 & .70
\end{array}\right]=\left[\begin{array}{lll}
.4224 & .5776
\end{array}\right] \nonumber \]

After 20 years the market share are given by $\mathrm{V}_{20}=\mathrm{V}_{0} \mathrm{T}^{20}=\left[\begin{array}{ll}
3 / 7 & 4 / 7
\end{array}\right]$.

After 21 years, $\mathrm{V}_{21}=\mathrm{V}_{0} \mathrm{T}^{21}=[3 / 7 \quad 4 / 7]$; market shares are stable and did not change.

The market share after 20 years has stabilized to $\left[\begin{array}{ll}
3 / 7 & 4 / 7
\end{array}\right]$. This means that

\[ \left[\begin{array}{lll}
3/7 & 4/7
\end{array}\right] \left[\begin{array}{ll}
.60 & .40 \\
.30 & .70
\end{array}\right]= \left[\begin{array}{lll}
3 / 7 & 4 / 7
\end{array}\right] \nonumber \]

Once the market share reaches an equilibrium state, it stays the same, that is, ET = E.

This helps us answer the next question.

Exercise $\PageIndex{3}$

Can the equilibrium vector E be found without raising the transition matrix T to large powers?

Answer

The answer to the second question provides us with a way to find the equilibrium vector E. The answer lies in the fact that ET = E.

Since we have the matrix T, we can determine E from the statement ET = E.

Suppose $\mathrm{E}=\left[\begin{array}{ll}
\mathrm{e} & 1-\mathrm{e}
\end{array}\right]$, then ET = E gives us

\[\left[\begin{array}{ll}
\mathrm{e} & 1-\mathrm{e}
\end{array}\right]\left[\begin{array}{ll}
.60 & .40 \\
.30 & .70
\end{array}\right]=\left[\begin{array}{lll}
\mathrm{e} & 1-\mathrm{e}
\end{array}\right] \nonumber \]

\[ \left[\begin{array}{ll}
(.60)\mathrm{e}+.30(1-\mathrm{e}) & (.40)\mathrm{e}+.70(1-\mathrm{e})
\end{array}\right] = \left[\begin{array}{ll}
\mathrm{e} & 1-\mathrm{e}
\end{array}\right] \nonumber \]

\[ \left[\begin{array}{ll}
.30\mathrm{e}+.30 & -.30\mathrm{e}+.70
\end{array}\right] = \left[\begin{array}{ll}
\mathrm{e} & 1-\mathrm{e}
\end{array}\right] \nonumber \]

\[.30\mathrm{e}+.30 = \mathrm{e} \nonumber \]

\[\mathrm{e} = 3/7 \nonumber \]

Therefore, $\mathrm{E}=\left[\begin{array}{ll}
3 / 7 & 4 / 7
\end{array}\right]$

As a result of our work in Exercise $\PageIndex{2}$ and $\PageIndex{3}$, we see that we have a choice of methods to find the equilibrium vector.

Method 1: We can determine if the transition matrix T is regular. If T is regular, we know there is an equilibrium and we can use technology to find a high power of T.

For the question of what is a sufficiently high power of T, there is no “exact” answer.
Select a “high power”, such as $n=30$, or $n=50$, or $n=98$. Evaluate Tⁿ on your calculator or with a computer. Check if Tⁿ⁺¹ = Tⁿ. If Tⁿ⁺¹ = Tⁿ and all the rows of Tⁿ are the same, then we’ve found the equilibrium. The equilibrium vector is one row of Tⁿ. But if you did not find equilibrium yet for a regular Markov chain, try using a higher power of T.

Method 2: We can solve the matrix equation ET=E.

The disadvantage of this method is that it is a bit harder, especially if the transition matrix is larger than $2 \times 2$. However it’s not as hard as it seems, if T is not too large a matrix, because we can use the methods we learned in chapter 2 to solve the system of linear equations, rather than doing the algebra by hand.
The advantage of solving ET = E as in Method 2 is that it can be used with matrices that are not regular. If a matrix is regular, it is guaranteed to have an equilibrium solution. If a matrix is not regular, then it may or may not have an equilibrium solution, and solving ET = E will allow us to prove that it has an equilibrium solution even if the matrix is not regular. (In mathematics we say that being a regular matrix is a “sufficient” condition for having an equilibrium, but is not a necessary condition.)

Exercise $\PageIndex{4}$

Does the long term market share for a Markov chain depend on the initial market share?

Answer

We will show that the final market share distribution for a Markov chain does not depend upon the initial market share. In fact, one does not even need to know the initial market share distribution to find the long term distribution.

Furthermore, the final market share distribution can be found by simply raising the transition matrix to higher powers.

Consider the initial market share $\mathrm{V}_{0}=\left[\begin{array}{ll}
.20 & .80
\end{array}\right]$, and the transition matrix $\mathrm{T}=\left[\begin{array}{ll}
.60 & .40 \\
.30 & .70
\end{array}\right]$ for BestTV and CableCast in the above example.

Recall we found Tⁿ, for very large $n$, to be $\left[\begin{array}{ll}
3 / 7 & 4 / 7 \\
3 / 7 & 4 / 7
\end{array}\right]$.

Using our calculators, we can easily verify that for sufficiently large $n$ (we used $n = 30$),

\[\mathrm{V}_{0} \mathrm{T}^{\mathrm{n}}=\left[\begin{array}{ll}
.20 & .80
\end{array}\right]\left[\begin{array}{ll}
3 / 7 & 4 / 7 \\
3 / 7 & 4 / 7
\end{array}\right]=\left[\begin{array}{lll}
3 / 7 & 4 / 7
\end{array}\right] \nonumber \]

No matter what the initial market share, the product is $\left[\begin{array}{ll}
3 / 7 & 4 / 7
\end{array}\right]$. If instead the initial share is $\mathrm{W}_0=\left[\begin{array}{ll}
.10 & .90
\end{array}\right]$, then for sufficiently large $n$

\[\mathrm{W}_{0} \mathrm{T}^{\mathrm{n}}=\left[\begin{array}{lll}
.10 & .90
\end{array}\right]\left[\begin{array}{ll}
3 / 7 & 4 / 7 \\
3 / 7 & 4 / 7
\end{array}\right]=\left[\begin{array}{ll}
3 / 7 & 4 / 7
\end{array}\right] \nonumber \]

For any distribution $A=\left[\begin{array}{ll}
a & 1-a
\end{array} |\right.$, for example,

\[\left[\begin{array}{ll}
a & 1-a
\end{array}\right]\left[\begin{array}{ll}
3 / 7 & 4 / 7 \\
3 / 7 & 4 / 7
\end{array}\right]=\left[\begin{array}{ll}
3 / 7(a)+3 / 7(1-a) & 4 / 7(a)+4 / 7(1-a)
\end{array}\right] \nonumber \]

\[=\left[\begin{array}{ll}
3 / 7 & 4 / 7
\end{array}\right] \nonumber \]

It makes sense; the entry $3/7(a) + 3/7(1 - a)$, for example, will always equal 3/7.

Example $\PageIndex{2}$

Three companies, A, B, and C, compete against each other. The transition matrix T for people switching each month among them is given by the following transition matrix.

Next Month

$Example10.3.2.png$

If the initial market share for the companies A, B, and C is $\left[\begin{array}{lll}
.25 & .35 & .40
\end{array}\right]$, what is the long term distribution?

Solution

Since the long term market share does not depend on the initial market share, we can simply raise the transition market share to a large power and get the distribution.

\[\mathrm{T}^{20}=\left[\begin{array}{lll}
13 / 55 & 3 / 11 & 27 / 55
\end{array}\right] \nonumber \]

In the long term, Company A has 13/55 (about 23.64%) of the market share, Company B has 3/11 (about 27.27%) of the market share, and Company C has 27/55 (about 49.09%) of the market share.

We summarize as follows:

Regular Markov Chains

A Markov chain is said to be a Regular Markov chain if some power of it has only positive entries.

Let T be a transition matrix for a regular Markov chain.

As we take higher powers of T, Tⁿ, as $n$ becomes large, approaches a state of equilibrium.
If V₀ is any distribution vector, and E an equilibrium vector, then V₀Tⁿ = E.
Each row of the equilibrium matrix Tⁿ is a unique equilibrium vector E such that ET = E.
The equilibrium distribution vector E can be found by letting ET = E.

Learning Objectives

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Regular Markov Chains