4.12: Applied Examples of Functions
- Page ID
- 45174
Applied examples of function (AKA word problems!) can take many forms.
Be prepared to use any type of function that has been reviewed in this chapter.
A summer job pays time and a half for overtime if a worker works more than 40 hours. After 40 hours, the worker is paid 1.5 times the hourly rate of \($12.00\) per hour.
- Write and graph a piece-wise function that gives the weekly pay P in terms of the number of hours worked h. HINT: This can be tricky, think about how to express the number of hours above 40.
- How much will be earned working 45 hours?
Solution
- To write the piece-wise function:
\(P (h) = \left\{\begin{array}{cc} 12h &0 < h \leq 40 \\ 12(40) + 1.5(12)(h − 40) &h > 40\end{array} \right.\)
To graph this function, make a table of solutions:
|
Table of Solutions for \(P (h) = 12h \) Domain \(0 < h \leq 40\) |
|
| \(h\) | \(P(h)\) |
| 1 | \($12.00\) |
| 10 | \($120.00\) |
| 40 | \($480.00\) |
|
Table of Solutions for \(P (h) = 12(40) + 1.5(7)(h − 40) \) Simplified \(P (h) = 18h − 240 \) Domain \(h > 40\) |
|
| \(h\) | \(P(h)\) |
| 41 | 498 |
| 45 | 570 |
| 50 | 660 |
| 60 | 840 |
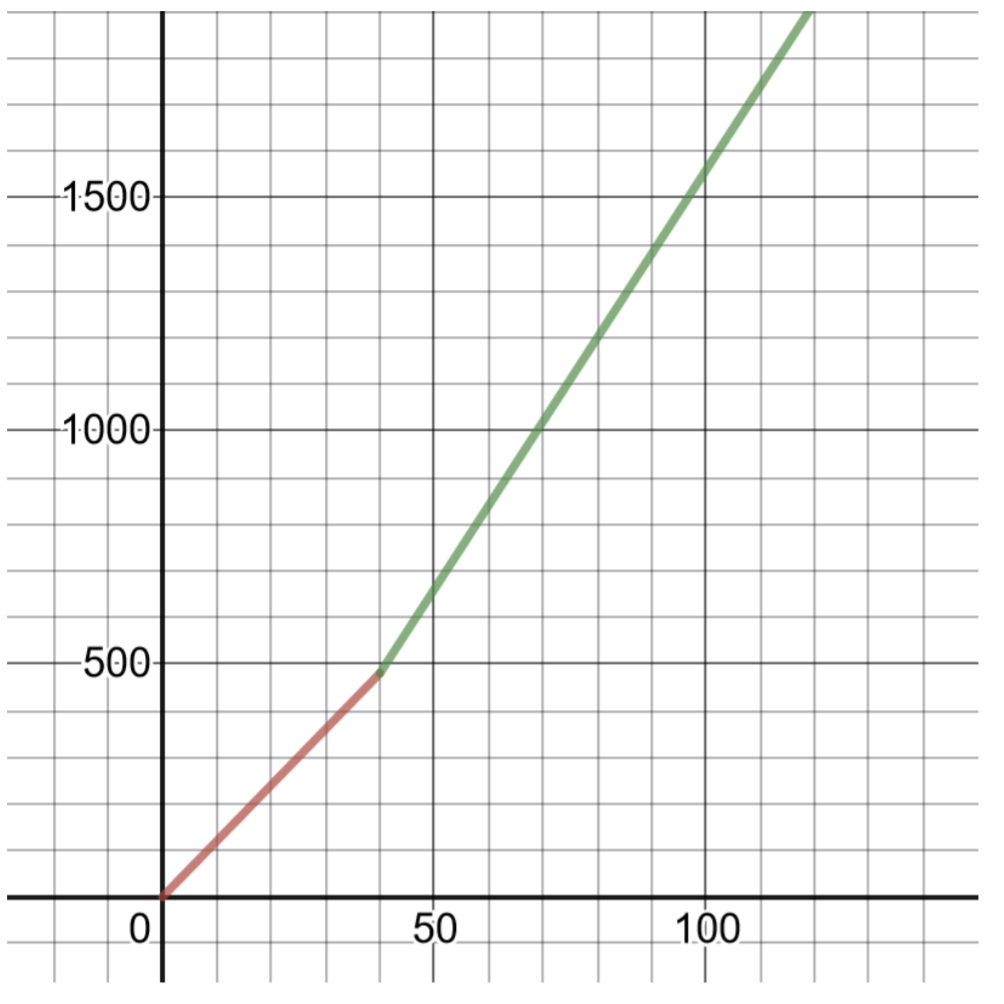
- \($570.00\) for 45 hours of work (see Table of Solutions)
NASA launches a rocket at \(t=0\) seconds. Its height, in meters above sea-level, as a function of time is given by \(h(t) = −4.9t^2 + 46t + 227\).
- Assuming that the rocket will splash down into the ocean, at what time does splashdown occur?
- How high above sea-level does the rocket get at its peak?
Solution
- At splash down, \(h(t) = 0\), so set the function equal to 0 and solve for \(t\).
\(0 = −4.9t 2 + 46t + 227\)
Use the Quadratic Formula to solve this equation, with \(a = −4.9\), \(b = 46\), \(c = 227\)
\(\begin{aligned} t &= \dfrac{−46 \pm \sqrt{46^2 − 4(−4.9)(227) }}{2(−4.9) } && \text{Quadratic Formula} \\ t &= \dfrac{−46 \pm \sqrt{ 2116 + 4449.2 }}{−9.8 } &&\text{Simplify the radical} \\ t &= \dfrac{46 \pm \sqrt{ 6565.2 }}{9.8 } &&\text{Further simplify the radical, divide all terms by -1 (still have } \pm\text{ )} \\t &= \dfrac{46 \pm 81.026 }{9.8 } &&\text{Square root} \\ t &= \dfrac{46 + 81.026 }{9.8 } &&\text{Addition} \\ t &= \dfrac{46 − 81.026 }{9.8} && \text{Subtraction} \\ t& = 12.96 \text{ and } t = −3.57&& \text{Two solutions, reject negative solution because time cannot be negative} \\ t &= 12.96 \text{ seconds }&&\text{Final Answer} \end{aligned}\)
- How high above sea-level does the rocket get at its peak?
The sign of the coefficient of the leading term of the quadratic function \(h(t) = −4.9t^2 + 46t + 227\) shows which way the parabola opens. The coefficient is \(−4.9\), and since it’s negative, the quadratic function opens downward.
Now we need to find the vertex. The y-value of the vertex ordered pair will show where the range begins.
The vertex is \(\left(− \dfrac{b }{2a} , f\left( −\dfrac{ b }{2a}\right) \right)\), with \(a = −4.9\) and \(b = 46\)
The vertex is \(\left(−\dfrac{ 46 }{2(−4.9) }, f\left( − \dfrac{46 }{2(−4.9)}\right)\right)\)
The vertex is \((4.694, f (4.694))\) which is \((4.694, (−4.9)(4.694)^2 + (46)(4.694) + 227 ))\) or \((4.694, 334.959)\)
The height of the rocket at its peak is \(334.959\) meters above sea level.
To promote group sales for an Alaskan cruise, a travel agency reduces the regular ticket price of \($4500\) by \($5\) for each person in the group.
- Write a linear equation that gives the per-person cost \(f(p)\), if \(p\) people travel in the group.
- Use the equation to determine the cost for 50 people.
Solution
- Since the per-person cost is reduced the same amount for each person, this is a linear equation.
Use \(f(x) = mx + b\), or let’s write it as \(f(p) = mp + b\), with \(f(p)\) the per-person cost.
\(f(p) = mp + b\)
Since the per-person cost is reduced by $5 for each person in the group, that is the slope of the line.
\(\begin{aligned} f(p)&= −5p + b && \text{Slope-intercept form of the equation of a line} \\ f(p) &= −5p + 4500 &&\text{The y-intercept is the starting point, so the regular ticket price of }$4500 {is the y-intercept} \\ f(p)& = −5p + 4500 && \text{Linear Equation} \end{aligned}\)
- Use the equation to determine the cost for 50 people.
\(\begin{aligned} f(50) &= −5(50) + 4500 && \text{Replace p with 50 people in the Linear Equation} \\ f(50) &= −250 + 4500 &&\text{Simplify} \\ f(50) &= 4250 &&\text{Simplify} \\ \text{If }50 &\text{ people take the cruise, the cost per-person for the cruise is } $4250&&\text{Final Answer }\end{aligned}\)
Complete the following applied function problems:
- A tailor charges a basic fee of \($20\) plus \($5\) per letter to sew an athlete’s name on the back of a jacket.
- Write a linear equation that will find the cost to have a name containing x letters sewn on the back of a jacket.
- What is the cost for a name with 11 letters?
- In Acapulco, Mexico, a popular tourist attraction is to watch men diving from a cliff to the water 75 feet below. A diver’s height \(f(t)\) above the water (in feet), \(t\) seconds after diving, is given by \(f(t) = −16t^2+75\).
- How long does a dive last?
- In a certain country, income tax is assessed as follows: There is no tax on income up to \($15000\). Income over \($15000\) and up to \($30000\) is taxed at \(12%\). Income over \($30000\) is taxed at \(18%\).
- Write the piecewise function of the above information and sketch its graph.
- Determine the amount of tax to be paid on an income of \($18000\).


