Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

7.5: Forms of the Equation of a Line

Last updated

Dec 15, 2024
Save as PDF
- 7.4: Equations of Vertical and Horizontal Lines
- 7.6: Applied Examples

Victoria Dominguez, Cristian Martinez, & Sanaa Saykali
Citrus College via ASCCC Open Educational Resources Initiative

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

The previous section explained the equations of vertical and horizontal lines. Now discover three more forms of the equations of a line, namely, the Slope-Intercept Form, the Point-Slope Form, and the Standard Form.

Slope-Intercept Form of the Equation of a Line

Definition: Slope-Intercept Form

The Slope-Intercept Form of the equation of a line is of the form:

$y = mx + b \nonumber$

Where $m$ is the slope of the line and $(0, b)$ is the $y$ −intercept.

Note that the $y$ -intercept is the point where the line intersect the $y$ −axis, that is when $x = 0$ .

Example 7.5.1

Write an equation of the line with the given slopes and $y$ -intercepts.

slope = $5$ ; $y$ −intercept $(0, \dfrac{1}{2})$
slope = $−\dfrac{5}{6}$ ; $y$ − intercept $(0, −\dfrac{3}{4})$

Solution

$m = 5$ and $b = \dfrac{1}{2}$

The equation of a line is of the for $y = mx + b$ . Thus,

$\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= 5x + \dfrac{1}{2} &\text{Substitute $m = 5$ and $b = \dfrac{1}{2}$} \end{array}$

Therefore, $y = 5x + \dfrac{1}{2}$ is the equation of the line with the given slope and $y$ -intercept.

Given $m = −\dfrac{5}{6}$ and $b = −\dfrac{3}{4}$

Thus,

$\begin{array} &&y = mx + b &\text{Slope-intercept form} \\ &= −\dfrac{5}{6}x −\dfrac{3}{4} &\text{Substitute values} \end{array}$

Therefore, $y = −\dfrac{5}{6}x − \dfrac{3}{4}$ is the equation of the line with the given slope and $y$ -intercept.

Example 7.5.2

Identify the slope and $y$ −intercept then, use them to graph each line.

$y = −2x + 4$
$5y − 3x = 10$

Solution

a. Notice that the given linear equation is in the slope-intercept form. So, $m = −2$ or equivalently, $m = −\dfrac{2}{1}$ and $b = 4$

$m$ is the slope of the line, then $m = \dfrac{\text{rise}}{\text{run}} = −\dfrac{2}{1}$ . To graph the line, plot at least two points. Start at the $y$ −intercept $(0, 4)$ and move down $2$ unit then move to the right $1$ unit to plot the second point. Now join the two points with a straight line as shown in the figure below.

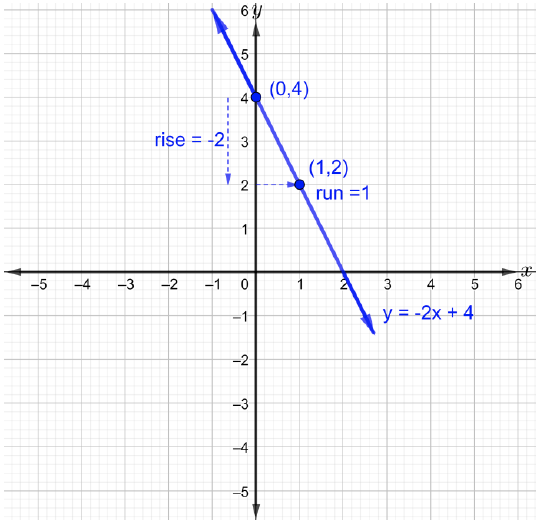
$clipboard_e5fcc0c548a6809df50a713b48295362a.png$

b. Notice that it is not clear how to identify the slope and $y$ -intercept in this given linear equation because it is not in the slope-intercept form. Thus, solve for $y$ to have the equation in the slope-intercept form as follows,

$\begin{array} &&5y − 3x = −10 &\text{Given} \\ &5y = 3x − 10 &\text{Add $3x$ to both sides of the equation} \\ &y = \dfrac{3}{5}x − 2 &\text{Divide all terms by $5$ to isolate $y$} \end{array}$

Now, $m = \dfrac{3}{5}$ and $b = −2$ . Start by plotting the $y$ -intercept $(0, −2)$ then move $3$ units upward and $5$ units to the right and plot the second point which is $(5, 1)$ . Now, join the two points, namely, $(0, −2)$ and $(5, 1)$ to get the graph of the line shown in the figure below.

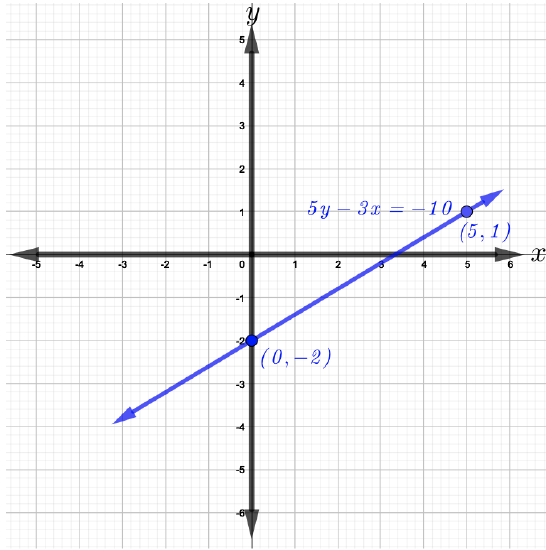
$clipboard_eca3205bebd002556f4570dc0193cd9f6.png$

Exercise 7.5.1

Write an equation of a line with the given slope and $y$ -intercept.

slope: $2$ $y$ -intercept: $(0, \dfrac{3}{4})$
slope: $\dfrac{5}{7}$ $y$ -intercept: $(0, −6)$
slope: $−\dfrac{1}{2}$ $y$ -intercept: $(0, −\dfrac{7}{11} )$

Exercise 7.5.2

Identify the slope and $y$ -intercept then use them to graph each line.

$y = 5x − 3$
$2y = −6x + 1$

Point-Slope Form of the Equation of a Line

Definition: Point-Slope Form

The Point-Slope Form of the equation of a straight line is:

$y − y_1 = m(x − x_1) \nonumber$

Where $m$ is the slope of the line and $(x_1, y_1)$ is any point on the straight line.

Example 7.5.3

Find the equation of each line passing through the given point and given slope.

Slope $3$ and point $(−1, 8)$
Slope $−\dfrac{5}{2}$ and point $(\dfrac{4}{3}, \dfrac{1}{3})$

Solution

To find the equation of the line through the point $(−1, 8)$ with slope $m = 3$ , use the point-slope form as follows:

$\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ &y − 8 = 3[x − (−1)] &\text{Substitute $m = 3$, $x_1 = −1$, and $y_1 = 8$} \\ &y − 8 = 3(x + 1) &\text{Simplify} \\ &y − 8 = 3x + 3 &\text{Multiply both terms on the right of the equation by $3$} \\ &y = 3x + 11 &\text{Add $8$ to both sides of the equality to isolate $y$} \end{array}$

Therefore, $y = 3x + 11$ is the equation of the line with the given slope and point. The line is in the slope-intercept form.

Similar to part a, use the Point-Slope Form as follows:

$\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-Slope form} \\ & y−(−\dfrac{1}{3}) = −\dfrac{5}{2} (x −\dfrac{4}{3}) &\text{Substitute $m = −\dfrac{5}{2},\;\; x_1 = \dfrac{4}{3}$, and $y_1 = −\dfrac{1}{3}$} \\ &y + \dfrac{1}{3} = −\dfrac{5}{2}x + \dfrac{20}{6} &\text{Distribute and simplify} \\ &y = −\dfrac{5}{2}x + \dfrac{20}{6} − \dfrac{1}{3} &\text{Subtract $\dfrac{1}{3}$ from both sides} \\ &y = −\dfrac{5}{2}x + 3 &\text{To combine the two fractions, notice that the LCD $= 6$.} \\ & &\text{Multiply numerator and denominator of $\dfrac{1}{3}$ by $2$ and simplify:} \\ & &\text{$\dfrac{20}{6} − \dfrac{1(2)}{3(2)} = \dfrac{20}{6} − \dfrac{2}{6} = \dfrac{18}{6} = 3$} \end{array}$

Therefore, $y = −\dfrac{5}{2}x + 3$ is the equation of the line through the give point and the given slope.

Example 7.5.4

Find an equation of the line given points $(2, 4)$ and $(−3, 9)$ .

Notice that earlier in this chapter it explained how to find an equation of a line given a slope and $y$ -intercept. This chapter also explained how to find an equation of a line given any point on the line and a slope. So, in both methods, the slope is given.

Solution

To find an equation of a line given any two points on the line, first find the slope using the slope of the line formula. After, apply the point-slope form with any of the given points. First, use the two points to find the slope of the line. Let $(x_1, y_1) = (2, 4)$ and $(x_2, y_2) = (−3, 9)$ . Then,

$\begin{array} &&m = \dfrac{y_2 − y_1}{x_2 − x_1} &\text{Slope of the line formula} \\ &= \dfrac{9 − 4}{−3 − 2} &\text{Substitute values} \\ &= \dfrac{5}{−5} &\text{Simplify} \\ &= −1 & \end{array}$

Now the slope has been found so next find the equation of the line using any one of the given points. Thus, $m = −1$ and consider using point $(2, 4)$ .

$\begin{array} &&y − y_1 = m(x − x_1) &\text{Point-slope form} \\ &y − 4 = −1(x − 2) &\text{Substitute $m = −1$, $x_1 = 2$, $y_1 = 4$} \\ &y − 4 = −x + 2 &\text{Distribute $-1$ to both terms on the right} \\ &y = −x + 6 &\text{Add $4$ to both sides of the equation to isolate $y$} \end{array}$

Therefore, $y = −x + 6$ is the equation of the line passing through the giving point and has the slope-intercept form.

Exercise 7.5.3

Find the equation of each line passing through the given point and has the given slope.

The slope $−\dfrac{5}{2}$ and the point $(3, 0)$ .
The slope $\dfrac{1}{2}$ and the point $(−2, −3)$ .

Exercise 7.5.4

Find an equation of the line given the following Points.

$(−9, −3)$ and $(6, −2)$
$(4, 1)$ and $(−2, 2)$

Standard Form of the Equation of a Line (AKA General Form of a Linear Equation)

Definition: Standard Form

The standard form of a non-vertical line is in the form

$Ax + By = C \nonumber$

Where $A$ is a positive integer, $B$ and $C$ are integers with $B \neq 0$ .

Example 7.5.5

Graph each line of the following equations:

$4x − 3y = 6$
$\dfrac{1}{2} − y + 1 = 0$

Note that the $x$ -intercept is the point where the line intersects the $x$ -axis. That is, when $y = 0$ . Thus, the $x$ -intercept is a point of the form $(a, 0)$ , where $a$ is any real number.

Solution

The equation $4x − 3y = 6$ is in standard form. To graph the line of the given equation it may be possible to use more than one method. For example, solving for $y$ to get the equation in slope-intercept form, then, graph the line. It’s also possible to find two points, then graph the line. The two easiest points to find quickly are the $x$ and $y$ intercepts. So, this method is recommended.

To find the $x$ -intercept, set $y = 0$ in the given equation and solve for $x$ as follows,

$\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4x − 3(0) = 6 &\text{Substitute $y = 0$} \\ &4x = 6 &\text{Simplify} \\ &x = \dfrac{6}{4} &\text{Divide by $4$ both sides of the equation} \\ &x = \dfrac{3}{2} &\text{Simplify} \end{array}$

Hence, the $x$ -intercept is the point $(\dfrac{3}{2}, 0)$

Now, to find the $y$ -intercept, set $x = 0$ as follows,

$\begin{array} &&4x − 3y = 6 &\text{Given} \\ &4(0) − 3y = 6 &\text{Substitute $x = 0$} \\ &−3y = 6 &\text{Simplify} \\ &y = 6 −3 &\text{Divide by $−3$ both sides of the equation} \\ &y = −2 &\text{Simplify} \end{array}$

Now, plot the points $(\dfrac{3}{2}, 0)$ and $(0, −2)$ and graph the straight line that passes through them as shown in the figure below.

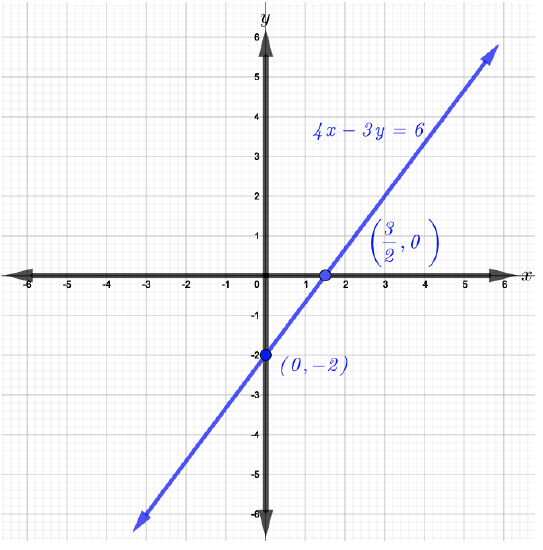
$clipboard_ede795f89eb03e5b448b62ec8dc0b7663.png$

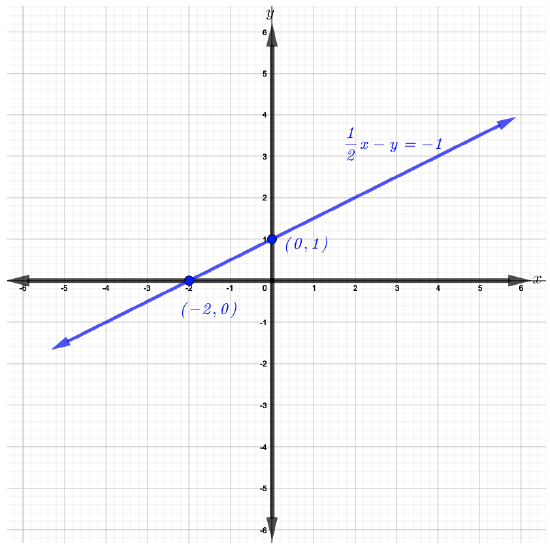
The equation $\dfrac{1}{2} x − y + 1 = 0$ is not in standard form. So, subtract $1$ from both sides of the equation to have $\dfrac{1}{2}x − y = −1$ which is now in standard form.

Again, similar to part b, find the $x$ and $y$ -intercepts. First, find the $x$ -intercept by setting $y = 0$ and solve for $x$ as follows.

$\begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}x − (0) = −1 &\text{Substitute $y = 0$} \\ &\dfrac{1}{2}x = −1 &\text{Simplify} \\ &x = −2 &\text{Multiply by $2$ both sides of the equation.} \end{array}$

Thus, the $x$ -intercept is the point $(−2, 0)$ .

Now, set $x = 0$ to find the $y$ -intercept, as follows,

$\begin{array} &&\dfrac{1}{2}x − y = −1 &\text{Standard form of the given equation} \\ &\dfrac{1}{2}(0) − y = −1 &\text{Substitute $x = 0$} \\ &−y = −1 &\text{Simplify} \\ &y = 1 &\text{Multiply by $-1$.} \end{array}$

Hence, the $y$ -intercept is $(0, 1)$ .

Plot the $x$ and $y$ -intercepts, $(−2, 0)$ and $(0, 1)$ , then graph the straight line that passes through them as shown in the figure below.

$clipboard_e3475016017c80b2298d3517f4bef3bf0.png$

There is no homework for this section.

Slope-Intercept Form of the Equation of a Line

Solution

Solution

Point-Slope Form of the Equation of a Line

Solution

Standard Form of the Equation of a Line (AKA General Form of a Linear Equation)

Solution

Support Center

How can we help?