5.8.1: Exercises

Last updated
Save as PDF

Page ID: 169545

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

For the following exercises, find the $x$- and $y$-intercepts on the graph.

Exercise $\PageIndex{1}$

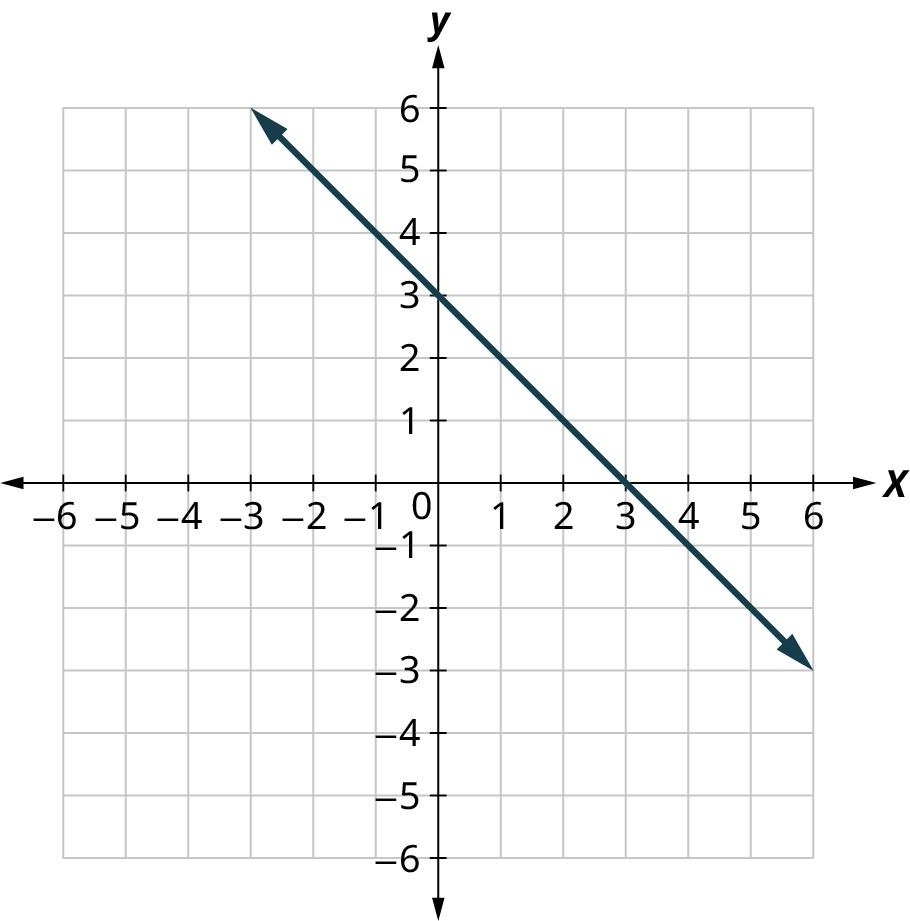
$A line is plotted on an x y coordinate plane. The x and y axes range from negative 6 to 6, in increments of 1. The line passes through the points, (negative 2, 5), (0, 3), (3, 0), and (6, negative 3). Note: all values are approximate.$

Exercise $\PageIndex{2}$

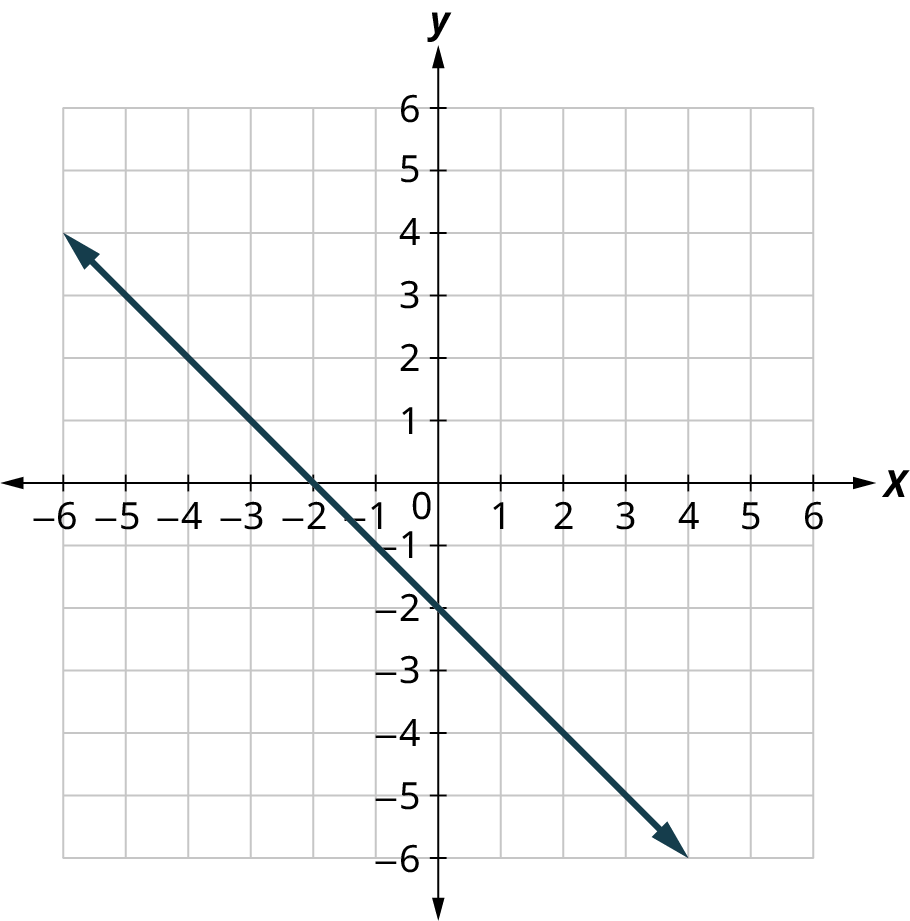
$A line is plotted on an x y coordinate plane. The x and y axes range from negative 6 to 6, in increments of 1. The line passes through the points, (negative 6, 4), (negative 2, 0), (0, negative 2), and (4, negative 6). Note: all values are approximate.$

Exercise $\PageIndex{3}$

$A line is plotted on an x y coordinate plane. The x and y axes range from negative 6 to 6, in increments of 1. The line passes through the points, (negative 1, negative 6), (0, negative 5), (5, 0), and (6, 1). Note: all values are approximate.$

Exercise $\PageIndex{4}$

$A line is plotted on an x y coordinate plane. The x and y axes range from negative 6 to 6, in increments of 1. The line passes through the points, (negative 3, negative 6), (0, 0), and (3, 6). Note: all values are approximate.$

For the following exercises, graph using the intercepts.

Exercise $\PageIndex{5}$

$- x + 4y = 8$

Exercise $\PageIndex{6}$

$x + y = - 3$

Exercise $\PageIndex{7}$

$4x + y = 4$

Exercise $\PageIndex{8}$

$3x - y = - 6$

Exercise $\PageIndex{9}$

$2x + 4y = 12$

Exercise $\PageIndex{10}$

$2x - 5y = - 20$

Exercise $\PageIndex{11}$

$y = - 2x$

Exercise $\PageIndex{12}$

$y = x$

For the following exercises, find the slope of the line.

Exercise $\PageIndex{13}$

$A line is plotted on an x y coordinate plane. The x and y axes range from negative 8 to 8, in increments of 1. The line passes through the points, (negative 5, negative 6), (0, negative 4), and (5, negative 2). Note: all values are approximate.$

Exercise $\PageIndex{14}$

$A line is plotted on an x y coordinate plane. The x and y axes range from negative 8 to 8, in increments of 1. The line passes through the points, (negative 4, negative 6), (0, negative 1), and (7.2, 8). Note: all values are approximate.$

Exercise $\PageIndex{15}$

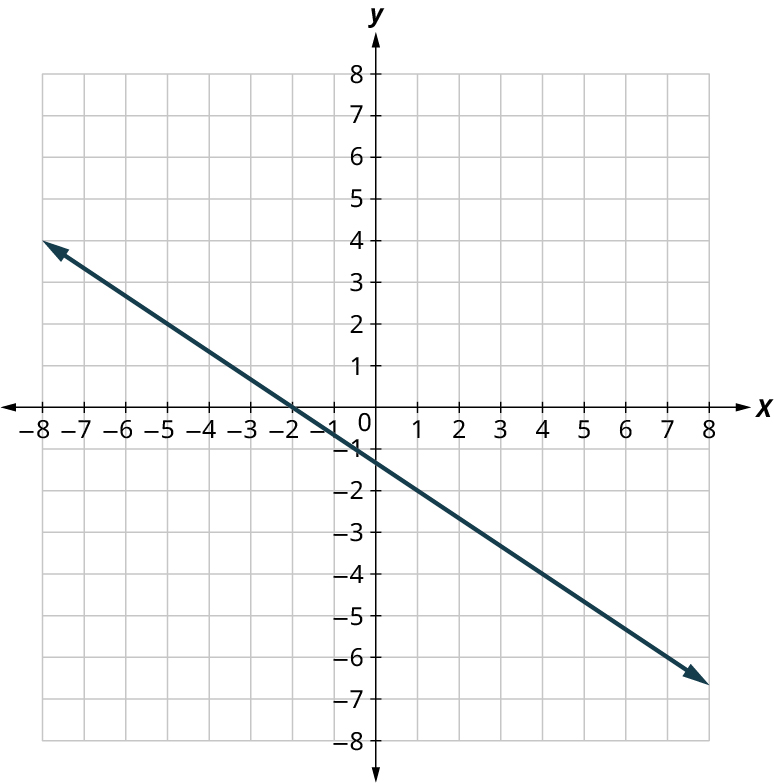
$A line is plotted on an x y coordinate plane. The x and y axes range from negative 8 to 8, in increments of 1. The line passes through the points, (negative 2, negative 8), (0, negative 5), (4, 1), and (8, 7). Note: all values are approximate.$

Exercise $\PageIndex{16}$

Exercise $\PageIndex{17}$

Exercise $\PageIndex{18}$

Exercise $\PageIndex{19}$

$A line is plotted on an x y coordinate plane. The x and y axes range from negative 8 to 8, in increments of 1. The line passes through the points, (negative 3, negative 7), (0, negative 2), (1, 0), and (6, 8). Note: all values are approximate.$

Exercise $\PageIndex{20}$

$A line is plotted on an x y coordinate plane. The x and y axes range from negative 8 to 8, in increments of 1. The line passes through the points, (negative 6, 4), (0, 2), and (6, 0). Note: all values are approximate.$

For the following exercises, use the slope formula to find the slope of the line between each pair of points.

Exercise $\PageIndex{21}$

(2, 5), (4, 0)

Exercise $\PageIndex{22}$

(−3, 3), (4, −5)

Exercise $\PageIndex{23}$

(−1, −2), (2, 5)

Exercise $\PageIndex{24}$

(4, −5), (1, −2)

For the following exercises, identify the slope and $y$-intercept of each line.

Exercise $\PageIndex{25}$

$y = - 7x + 3$

Exercise $\PageIndex{26}$

$y = 4x - 10$

Exercise $\PageIndex{27}$

$3x + y = 5$

Exercise $\PageIndex{28}$

$4x + y = 8$

Exercise $\PageIndex{29}$

$6x + 4y = 12$

Exercise $\PageIndex{30}$

$8x + 3y = 12$

Exercise $\PageIndex{31}$

$5x - 2y = 6$

Exercise $\PageIndex{32}$

$7x - 3y = 9$

For the following exercises, graph the line of each equation using its slope and $y$-intercept.

Exercise $\PageIndex{33}$

$y = 3x - 1$

Exercise $\PageIndex{34}$

$y = 2x - 3$

Exercise $\PageIndex{35}$

$y = - x + 3$

Exercise $\PageIndex{36}$

$y = - x - 4$

Exercise $\PageIndex{37}$

$y = - 2x - 3$

Exercise $\PageIndex{38}$

$y = - 3x + 2$

Exercise $\PageIndex{39}$

$3x - 2y = 4$

Exercise $\PageIndex{40}$

$3x - 4y = 8$

For the following exercises, find the slope of each line and graph.

Exercise $\PageIndex{41}$

$y = 3$

Exercise $\PageIndex{42}$

$y = - 2$

Exercise $\PageIndex{43}$

$x = - 5$

Exercise $\PageIndex{44}$

$x = 4$

For the following exercises, graph and interpret applications of slope-intercept.
The equation $P = 31 + 1.75w$ models the relation between the amount of Tuyet’s monthly water bill payment, $P$, in dollars, and the number of units of water, $w$, used.

Exercise $\PageIndex{45}$

Find Tuyet’s payment for a month when 0 units of water are used.

Exercise $\PageIndex{46}$

Find Tuyet’s payment for a month when 12 units of water are used.

Exercise $\PageIndex{47}$

Interpret the slope and $P$-intercept of the equation.

Exercise $\PageIndex{48}$

Graph the equation.

For the following exercises, graph and interpret applications of slope-intercept.
Bruce drives his car for his job. The equation $R = 0.575m + 42$ models the relation between the amount in dollars, $R$, that he is reimbursed and the number of miles, $m$, he drives in one day.

Exercise $\PageIndex{49}$

Find the amount Bruce is reimbursed on a day when he drives 0 miles.

Exercise $\PageIndex{50}$

Find the amount Bruce is reimbursed on a day when he drives 220 miles.

Exercise $\PageIndex{51}$

Interpret the slope and $R$-intercept of the equation.

Exercise $\PageIndex{52}$

Graph the equation.

For the following exercises, graph and interpret applications of slope-intercept.
Cherie works in retail and her weekly salary includes commission for the amount she sells. The equation $S = 400 + 0.15c$ models the relation between her weekly salary, $S$, in dollars and the amount of her sales, $c$, in dollars.

Exercise $\PageIndex{53}$

Find Cherie’s salary for a week when her sales were $0.

Exercise $\PageIndex{54}$

Find Cherie’s salary for a week when her sales were $3,600.

Exercise $\PageIndex{55}$

Interpret the slope and $S$-intercept of the equation.

Exercise $\PageIndex{56}$

Graph the equation.

For the following exercises, graph and interpret applications of slope-intercept.
Costa is planning a lunch banquet. The equation $C = 450 + 28g$ models the relation between the cost in dollars, $C$, of the banquet and the number of guests, $g$.

Exercise $\PageIndex{57}$

Find the cost if the number of guests is 40.

Exercise $\PageIndex{58}$

Find the cost if the number of guests is 80.

Exercise $\PageIndex{59}$

Interpret the slope and $C$-intercept of the equation.

Exercise $\PageIndex{60}$

Graph the equation.

Search

Text Color

Text Size

Margin Size

Font Type

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)

Exercise \(\PageIndex{15}\)

Exercise \(\PageIndex{16}\)

Exercise \(\PageIndex{17}\)

Exercise \(\PageIndex{18}\)

Exercise \(\PageIndex{19}\)

Exercise \(\PageIndex{20}\)

Exercise \(\PageIndex{21}\)

Exercise \(\PageIndex{22}\)

Exercise \(\PageIndex{23}\)

Exercise \(\PageIndex{24}\)

Exercise \(\PageIndex{25}\)

Exercise \(\PageIndex{26}\)

Exercise \(\PageIndex{27}\)

Exercise \(\PageIndex{28}\)

Exercise \(\PageIndex{29}\)

Exercise \(\PageIndex{30}\)

Exercise \(\PageIndex{31}\)

Exercise \(\PageIndex{32}\)

Exercise \(\PageIndex{33}\)

Exercise \(\PageIndex{34}\)

Exercise \(\PageIndex{35}\)

Exercise \(\PageIndex{36}\)

Exercise \(\PageIndex{37}\)

Exercise \(\PageIndex{38}\)

Exercise \(\PageIndex{39}\)

Exercise \(\PageIndex{40}\)

Exercise \(\PageIndex{41}\)

Exercise \(\PageIndex{42}\)

Exercise \(\PageIndex{43}\)

Exercise \(\PageIndex{44}\)

Exercise \(\PageIndex{45}\)

Exercise \(\PageIndex{46}\)

Exercise \(\PageIndex{47}\)

Exercise \(\PageIndex{48}\)

Exercise \(\PageIndex{49}\)

Exercise \(\PageIndex{50}\)

Exercise \(\PageIndex{51}\)

Exercise \(\PageIndex{52}\)

Exercise \(\PageIndex{53}\)

Exercise \(\PageIndex{54}\)

Exercise \(\PageIndex{55}\)

Exercise \(\PageIndex{56}\)

Exercise \(\PageIndex{57}\)

Exercise \(\PageIndex{58}\)

Exercise \(\PageIndex{59}\)

Exercise \(\PageIndex{60}\)