5.8: Graphing Functions
- Page ID
- 129560
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)After completing this module, you should be able to:
- Graph functions using intercepts.
- Compute slope.
- Graph functions using slope and -intercept.
- Graph horizontal and vertical lines.
- Interpret graphs of functions.
- Model applications using slope and -intercept.
In this section, we will expand our knowledge of graphing by graphing linear functions. There are many real-world scenarios that can be represented by graphs of linear functions. Imagine a chairlift going up at a ski resort. The journey a skier takes travelling up the chairlift could be represented as a linear function with a positive slope. The journey a skier takes down the slopes could be represented by a linear function with a negative slope.
Graphing Functions Using Intercepts
Every linear equation can be represented by a unique line that shows all the solutions of the equation. We have seen that when graphing a line by plotting points, you can use any three solutions to graph. This means that two people graphing the line might use different sets of three points. At first glance, their two lines might not appear to be the same, since they would have different points labeled. But if all the work was done correctly, the lines should be exactly the same. One way to recognize that they are indeed the same line is to look at where the line crosses the \(\bar{x}\)-axis and the \(y\)-axis. These points are called the intercepts of a line. Let us review the graphs of the lines in Figure \(\PageIndex{2}\).
The table below lists where each of these lines crosses the \(x\)- and -axis. Do you see a pattern? For each line, the -coordinate of the point where the line crosses the \(x\)-axis is zero. The point where the line crosses the \(x\)-axis has the form and is called the \(x\)-intercept of the line. The \(x\)-intercept occurs when is zero. In each line, the \(x\)-coordinate of the point where the line crosses the -axis is zero. The point where the line crosses the -axis has the form and is called the -intercept of the line. The -intercept occurs when \(x\) is zero.
| Figure | The line crosses the |
Ordered Pair for this Point | The line crosses the |
Ordered Pair for This Point |
|---|---|---|---|---|
| Figure (a) | 3 | 6 | ||
| Figure (b) | 4 | |||
| Figure (c) | 5 | |||
| Figure (d) | 0 | 0 | ||
| General Figure |
Find the \(x\)-intercept and -intercept on the (a) and (b) graphs in Figure \(\PageIndex{3}\).
- Answer
-
In Figure \(\PageIndex{3}\), the graph crosses the \(x\)-axis at the point \((4,0)\). The \(x\)-intercept is \((4,0)\). The graph crosses the \(y\)-axis at the point \((0,2)\). The \(y\)-intercept is \((0,2)\). In Figure 5.66 , the graph crosses the \(x\)-axis at the point \((2,0)\). The \(x\)-intercept is \((2,0)\). The graph crosses the \(y\)-axis at the point \((0,-6)\). The \(y\)-intercept is \((0,-6)\).
Find the \(x\)-intercept and \(y\)-intercept on the given graph.

Find the intercepts of \(2 x+y=8\). Then graph the function using the intercepts.
- Answer
-
Let to find the \(x\)-intercept, and let to find the-intercept.
\(2x+y=8\) \(2x+y=8\) To find the \(x\)-intercept, let \(y=0\)
.\(2x+0=8\) To find the \(y\) intercept let \(x=0\). \(2(0)+y=8\) Simplify. \(\begin{aligned} 2 x & =8 \\ x & =4\end{aligned}\) Simplify. \(y=8\) The \(x\)-intercept is: \((4,0)\) The \(y\)-intercept is: \((0,8)\) Plot the intercepts to get the graph in Figure \(\PageIndex{5}\).
Figure \(\PageIndex{5}\)
Find the intercepts of \(3x + y = 12\) and use them to graph the equation.
Computing Slope
When graphing linear equations, you may notice that some lines tilt up as they go from left to right and some lines tilt down. Some lines are very steep and some lines are flatter. In mathematics, the measure of the steepness of a line is called the slope of the line. To find the slope of a line, we locate two points on the line whose coordinates are integers. Then we sketch a right triangle where the two points are vertices of the triangle and one side is horizontal and one side is vertical. Next, we measure or calculate the distance along the vertical and horizontal sides of the triangle. The vertical distance is called the rise and the horizontal distance is called the run.
We can assign a numerical value to the slope of a line by finding the ratio of the rise and run. The rise is the amount the vertical distance changes while the run measures the horizontal change, as shown in this illustration. Slope (Figure \(\PageIndex{6}\)) is a rate of change.
To calculate slope \((m)\), use the formula
\[m=\dfrac{r i s e}{r u n} \nonumber \]
where the rise measures the vertical change and the run measures the horizontal change.
The concept of slope has many applications in the real world. In construction, the pitch of a roof, the slant of plumbing pipes, and the steepness of stairs are all applications of slope. As you ski or jog down a hill, you definitely experience slope.
Find the slope of the line shown in Figure \(\PageIndex{7}\).
- Answer
-
Step 1: Locate two points on the graph whose coordinates are integers, such as (0,5) and (3,3). Starting at (0,5), sketch a right triangle to (3,3) as shown in Figure \(\PageIndex{8}\).
Figure \(\PageIndex{8}\) Step 2: Count the rise; since it goes down, it is negative. The rise is −2.
Step 3: Count the run. The run is 3.
Step 4: Use the slope formula \(m=\frac{r i s e}{r u n}\) substitute the values of the rise and run. \(m=\frac{-2}{3}\)
The slope of the line is \(-\frac{2}{3}\).
The solution is \(y\) decreases by 2 units as \(x\) increases by 3 units.
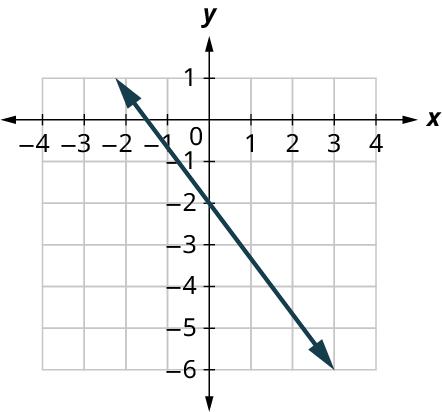
Find the slope of the line shown in the graph.
Sometimes we will need to find the slope of a line between two points when we don’t have a graph to measure the rise and the run. We could plot the points on grid paper, then count out the rise and the run, but there is a way to find the slope without graphing. First, we need to introduce some algebraic notation.
We have seen that an ordered pair \((x, y)\) gives the coordinates of a point. But when we work with slopes, we use two points. How can the same symbol \((x, y)\) be used to represent two different points? Mathematicians use subscripts to distinguish such points. For example, \(\left(x_1, y_1\right)\) would be said aloud as " \(x\) sub \(1, y\) sub 1 " and \(\left(x_2, y_2\right)\) read " \(x\) sub 2, \(y\) sub 2." The "sub" is a short way of saying "subscript." We will use ( \(x_1, y_1\) ) to identify the first point and \(\left(x_2, y_2\right)\) to identify the second point in our slope equation. If we had more than two points, (if we were finding more than one slope), we could use ( \(\left.x_3, y_3\right),\left(x_4, y_4\right)\), and so on.
Let's review how the rise and run relate to the coordinates of the two points by taking another look at the slope of the line between the points \((2,3)\) and \((7,6)\), as shown in Figure \(\PageIndex{10}\).
On the graph, we count the rise of 3 and the run of 5 . Notice on the graph that that \(\left(x_1, y_1\right)\) is the point \((2,3)\) and ( \(\left.x_2, y_2\right)\) is the point \((7,6)\). The rise can be found by subtracting the \(y\)-coordinates, 6 and 3 , and the run can be found by subtracting the \(x\)-coordinates 7 and 2 .
\[
m=\frac{r i s e}{r u n}=\frac{6-3}{7-2}=\frac{3}{5}
\nonumber \]
We have shown that \(m=\frac{y_2-y_1}{x_2-x_1}\) is really another version of \(m=\frac{r i s e}{r u n}\). We can use this formula to find the slope of a line.
To find the slope of the line between two points \(\left(x_1, y_1\right)\) and \(\left(x_2, y_2\right)\), use the formula
\[
m=\frac{y_2-y_1}{x_2-x_1}
\nonumber \]
Use the slope formula to find the slope of the line through the points (−2, −3) and (−7, 4).
- Answer
-
We'll call \((-2,-3)\) point 1 and \((-7,4)\) point 2.
Step 1: Use the slope formula: \(m=\frac{y_2-y_1}{x_2-x_1}\)
Step 2: Substitute the values: \(m=\frac{4-(-3)}{-7-(-2)}\)
Step 3: Simplify: \(m=\frac{7}{-5}=-\frac{7}{5}\)
Step 4: Verify the slope on the graph shown in Figure \(\PageIndex{11}\).
Figure \(\PageIndex{11}\): Copy and Paste Caption here. (Copyright; author via source)
Use the slope formula to find the slope of the line through the pair of points \((-3, 4)\) and \((2, -1)\).
Graphing Functions Using Slope and -Intercept
We have graphed linear equations by plotting points and using intercepts. Once we see how an equation in slopeintercept form and its graph are related, we will have one more method we can use to graph lines. Review the graph of the equation \(y=\frac{1}{2} x+3\) in Figure 5.73 and find its slope and \(y\)-intercept.
The vertical and horizontal lines in the graph show us the rise is 1 and the run is 2 , respectively.
Substituting into the slope formula: \(m=\frac{r i s e}{r u n}=\frac{1}{2}\)
The \(y\)-intercept is \((0,3)\). Look at the equation of this line.
\[y=\frac{1}{2} x+3 \nonumber \]
Look at the slope and \(y\)-intercept.
\[\text { slope } m=\frac{1}{2} \text { and } y \text {-intercept }(0,3) \nonumber \]
When a linear equation is solved for \(y\), the coefficient of the \(x\) term is the slope and the constant term is the \(y\) coordinate of the \(y\)-intercept. We say that the equation \(y=\frac{1}{2} x+3\) is in slope-intercept form. Sometimes the slope-intercept form is called the \(y\)-form.
Identify the slope and \(y\)-intercept of the line from the equation:
1. \(y=-\frac{4}{7} x-2\)
2. \(x+3 y=9\)
- Answer
-
1. We compare our equation to the slope-intercept form of the equation.
Step 1: Write the slope-intercept form of the equation of the line.
\[y=m x+b \nonumber \]
Step 2: Write the equation of the line.
\[y=-\frac{4}{7} x-2 \nonumber \]
Step 3: Identify the slope.
\[m=-\frac{4}{7} \nonumber \]
Step 4: Identify the \(y\)-intercept.
\[y \text {-intercept is }(0,-2) \nonumber \]
2. When an equation of a line is not given in slope-intercept form, our first step will be to solve the equation for \(y\).
Step 1: Solve for \(y\).
\[x+3 y=9 \nonumber \]
Step 2: Subtract \(x\) from each side.
\[3 y=-x+9 \nonumber \]
Step 3: Divide both sides by 3.
\[\frac{3 y}{3}=\frac{-x+9}{3} \nonumber \]
Step 4: Simplify.
\[y=-\frac{1}{3} x+3 \nonumber \]
Step 5: Write the slope-intercept form of the equation of the line.
\[y=m x+b \nonumber \]
Step 6: Write the equation of the line.
\[y=-\frac{1}{3} x+3 \nonumber \]
Step 7: Identify the slope.
\[m=-\frac{1}{3} \nonumber \]
Step 8: Identify the \(y\)-intercept.
\[y \text {-intercept is }(0,3) \nonumber \]
Identify the slope and \(y\)-intercept from the equation of the line.
- \(y = 2x - 1\)
- \(x + 4y = 16\)
Graph the line of the equation using its slope and -intercept.
- Answer
-
The equation is in slope-intercept form .
Step 1: Identify the slope and \(y\)-intercept.
\(m=-1, y\)-intercept is \((0,4)\).Step 2: Plot the \(y\)-intercept on the coordinate system (Figure 5.74).
1. Identify the rise over the run.
\[m=-1=\frac{-1}{1} \nonumber \]
2. Count out the rise and run to mark the second point. rise -1 , run 1
Figure \(\PageIndex{13}\)
Graph the line of the equation \(y = - x - 3\) using its slope and \(y\)-intercept.
Graphing Horizontal and Vertical Lines
Some linear equations have only one variable. They may have just \(x\) without the , or just without an \(x\). This changes how we make a table of values to get the points to plot. Let us consider the equation . This equation has only one variable, \(x\). The equation says that \(x\) is always equal to , so its value does not depend on . No matter what the value of is, the value of \(x\) is always . To make a table of values, write in for all the \(x\)-values. Then choose any values for . Since \(x\) does not depend on , you can choose any numbers you like. But to fit the points on our coordinate graph, we will use 1, 2, and 3 for the -coordinates in the table below.
| \(x\) | (\(x\), ) | |
| −3 | 1 | |
| 2 | ||
| 3 | ||
Plot the points from the table and connect them with a straight line (Figure \(\PageIndex{14}\)). Notice that we have graphed a vertical line.
What is the slope? If we take the two points \((-3,3)\) and \((-3,1)\) then the rise is 2 and the run is 0 .
Using the slope formula we get: \(m=\frac{r i s e}{r u n}=\frac{2}{0}\)
The slope is undefined since division by zero is undefined. We say that the slope of the vertical line \(x=-3\) is undefined. The slope of any vertical line \(x=a\) (where \(a\) is any number) will be undefined.
What if the equation has \(y\) but no \(x\) ? Let's graph the equation \(y=4\). This time the \(y\)-value is a constant, so in this equation, \(y\) does not depend on \(x\). Fill in 4 for all the \(y\) values in the table below and then choose any values for \(x\). We will use 0,2 , and 4 for the \(x\)-coordinates.
| \(x\) | (\(x\), ) | |
| 0 | 4 | |
| 2 | 4 | |
| 4 | 4 | |
In Figure \(\PageIndex{152}\), we have graphed a horizontal line passing through the -axis at 4.
What is the slope? If we take the two points \((2,4)\) and \((4,4)\) then the rise is 0 and the run is 2 . Using the slope formula, we get \(m=\frac{r i s e}{r u n}=\frac{0}{2}=0\). The slope of the horizontal line \(y=4\) is 0 . The slope of any horizontal line \(y=b\) (where \(b\) is any number) will be 0 . When the \(y\)-coordinates are the same, the rise is 0 .
Graph: .
- Answer
-
The equation has only one variable, \(x\), and \(x\) is always equal to 2 . We create a table where \(x\) is always 2 and then put in any values for \(y\). The graph is a vertical line passing through the \(x\)-axis at 2 (Figure \(\PageIndex{16}\)).
\(x\) (\(x\), ) 2 1 2 2 2 3 Figure \(\PageIndex{16}\)
Graph \(x = 5\).
Graph: .
- Answer
-
The equation \(y=-1\) has only one variable, \(y\). The value of \(y\) is constant. All the ordered pairs in the next table have the same \(y\)-coordinate. The graph is a horizontal line passing through the \(y\)-axis at -1 (Figure \(\PageIndex{17}\)).
\(x\) (\(x\), ) 0 3 Figure \(\PageIndex{17}\)
Graph the equation \(y = - 4\).
The table below summarizes all the methods we have used to graph lines.
Interpreting Graphs of Functions
An important yet often overlooked area in algebra involves interpreting graphs. Oftentimes in math classes, students are given mathematical functions and can make graphs to represent them. But the interpretation of graphs is a more applicable skill to the real world. Being able to “read” a graph—understanding its domain and range, what the intercepts mean, and what the slope (or curve) means— that's a real-world skill.
In Figure \(\PageIndex{18}\) the \(x\)-axis on the graph represents the 120-minute bike ride Juan went on. The -axis represents how far away he was from his home.
Figure \(\PageIndex{18}\)
- Interpret the \(x\)- and -intercept.
- For each segment, find the slope.
- Create an interpretation of this graph (i.e., make up a story that goes with it).
- Answer
-
- is the \(x\)- and -intercept and represents Juan at home before his bike ride. The distance from home is 0 miles and 0 minutes have passed.
- In the first 30 minutes, the slope is and indicates Juan is traveling 1 mile for every 5 minutes. Between 30 and 60 minutes, the slope is 0 and indicates that he’s not riding the bike (the distance is not increasing). Then between 60 and 90 minutes, the slope is again. Finally, after 90 minutes the slope is meaning Juan is getting 4 miles closer to home every 15 minutes.
- Answers will vary. Juan left his house for a bike ride. After 30 minutes, he was 6 miles from home and he stopped for ice cream at his local ice-cream truck. He enjoyed his ice cream for 30 minutes. He then jumped back on his bike and rode to his friend’s house. He arrived there 30 minutes later. His friend’s house was 12 miles from his home. His friend was not home so he immediately turned around and quickly rode home in 45 minutes.
In the given figure the \(x\)-axis on the graph represents the years. The y-axis represents the number of teachers at Jones High School.

Interpret the \(x\)- and \(y\)-intercept.
For each segment, find the slope.
Create an interpretation of this graph (i.e., make up a story that goes with it).
Modeling Applications Using Slope and -Intercept
Many real-world applications are modeled by linear equations. We will review a few applications here so you can understand how equations written in slope-intercept form relate to real-world situations. Usually when a linear equation model uses real-world data, different letters are used for the variables instead of using only \(x\) and . The variable names often remind us of what quantities are being measured. Also, we often need to extend the axes in our rectangular coordinate system to bigger positive and negative numbers to accommodate the data in the application.
The equation
- Find the Fahrenheit temperature for a Celsius temperature of 0°.
- Find the Fahrenheit temperature for a Celsius temperature of 20°.
- Interpret the slope and -intercept of the equation.
- Graph the equation.
- Answer
-
- Find the Fahrenheit temperature for a Celsius temperature of 0°.
Find \(F\) when \C=0\) \(F=\frac{9}{5}(0)+32\) Simplify. \(F=32\) - Find the Fahrenheit temperature for a Celsius temperature of 20°.
Find \(F\) when \C=20\) \(F=\frac{9}{5}(20)+32\) Simplify. \(F=36 + 32\) Simplify. \(F=68\) 3. Interpret the slope and \(F\)-intercept of the equation.
Even though this equation uses \(F\) and \(C\), it is still in slope-intercept form.
\[\begin{array}{l}
y=m x+b \\
F=m C+b \\
F=\frac{9}{5} C+32
\end{array} \nonumber \]The slope \(\frac{9}{5}\) means that the temperature Fahrenheit \((F)\) increases 9 degrees when the temperature Celsius \((C)\) increases 5 degrees.
The \(F\)-intercept means that when the temperature is \(0^{\circ}\) on the Celsius scale, it is \(32^{\circ}\) on the Fahrenheit scale.
4. Graph the equation.
We will need to use a larger scale than our usual. Start at the \(F\)-intercept \((0,32)\), and then count out the rise of 9 and the run of 5 to get a second point as shown in Figure \(\PageIndex{20}\).
Figure \(\PageIndex{20}\): Copy and Paste Caption here. (Copyright; author via source) - Find the Fahrenheit temperature for a Celsius temperature of 0°.
The equation \(h = 2s + 50\) is used to estimate a person’s height in inches, \(h\), based on women’s shoe size, \(s\).
- Estimate the height of a child who wears women’s shoe size 0.
- Estimate the height of a woman with shoe size 8.
- Interpret the slope and \(h\)-intercept of the equation.
- Graph the equation.
Sam drives a delivery van. The equation \(C=0.5 d+60\) models the relation between his weekly cost, \(C\), in dollars and the number of miles, \(d\), that he drives.
- Find Sam’s cost for a week when he drives 0 miles.
- Find the cost for a week when he drives 250 miles.
- Interpret the slope and -intercept of the equation.
- Graph the equation.
- Answer
-
- Find Sam’s cost for a week when he drives 0 miles.
Find \(C\) when \(d=0\). Simplify. Sam’s costs are $60 when he drives 0 miles.
- Find the cost for a week when he drives 250 miles.
Find \(C\) when \(d=250\). Simplify. Sam’s costs are $185 when he drives 250 miles.
3. Interpret the slope and \(C\)-intercept of the equation.
\[\begin{array}{l}
y=m x+b \\
C=0.5 d+60
\end{array} \nonumber \]The slope, 0.5 , means that the weekly cost, \(C\), increases by \(\$ 0.50\) when the number of miles driven, \(d\), increases by 1 . The \(C\)-intercept means that when the number of miles driven is 0 , the weekly cost is \(\$ 60\).
4. Graph the equation (Figure \(\PageIndex{21}\)).We'll need to use a larger scale than usual. Start at the \(C\)-intercept ( 0,60 ). To count out the slope \(m=0.5\), we rewrite it as an equivalent fraction that will make our graphing easier.
\[m=0.5=\frac{5}{10}=\frac{50}{100} \nonumber \]
So to graph the next point go up 50 from the intercept of 60 and then to the right 100 . The second point will be \((100,110)\).
Figure \(\PageIndex{21}\): Copy and Paste Caption here. (Copyright; author via source) - Find Sam’s cost for a week when he drives 0 miles.
Stella has a home business selling gourmet pizzas. The equation \(C = 4p + 25\) models the relation between her weekly cost, \(C\), in dollars and the number of pizzas, \(p\), that she sells.
- Find Stella’s cost for a week when she sells no pizzas.
- Find the cost for a week when she sells 15 pizzas.
- Interpret the slope and \(C\)-intercept of the equation.
- Graph the equation.
Check Your Understanding
- True or False. The \(x\)-intercept of \(y = {\text{ }}2x{\text{ }}-8{\text{ is }}\left( {0,-8} \right)\).
- True or False. The slope of the line containing the points (1, 2) and (2, 4) is 1.
For the following exercises, use the graph shown.

3. True or False. This graph has a slope of 5.
4. True or False. This is the graph of the equation \(y = {\text{ }}4x + 5\).
5. True or False. All vertical lines have a slope of zero.


