10.3: Angles

Last updated
Save as PDF

Page ID: 129641

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

The exterior view of an architectural building.

Figure 10.26 This modern architectural design emphasizes sharp reflective angles as part of the aesthetic through the use of glass walls. (credit: “Société Générale @ La Défense @ Paris” by Images Guilhem Vellut/Flickr, CC BY 2.0)

Learning Objectives

After completing this section, you should be able to:

Identify and express angles using proper notation.
Classify angles by their measurement.
Solve application problems involving angles.
Compute angles formed by transversals to parallel lines.
Solve application problems involving angles formed by parallel lines.

Unusual perspectives on architecture can reveal some extremely creative images. For example, aerial views of cities reveal some exciting and unexpected angles. Add reflections on glass or steel, lighting, and impressive textures, and the structure is a work of art. Understanding angles is critical to many fields, including engineering, architecture, landscaping, space planning, and so on. This is the topic of this section.

We begin our study of angles with a description of how angles are formed and how they are classified. An angle is the joining of two rays, which sweep out as the sides of the angle, with a common endpoint. The common endpoint is called the vertex. We will often need to refer to more than one vertex, so you will want to know the plural of vertex, which is vertices.

In Figure 10.27, let the ray $\vec{A B}$ stay put. Rotate the second ray $\vec{A C}$ in a counterclockwise direction to the size of the angle you want. The angle is formed by the amount of rotation of the second ray. When the ray $\vec{A C}$ continues to rotate in a counterclockwise direction back to its original position coinciding with ray $\vec{A B},$ the ray will have swept out $360^{\circ} .$ We call the rays the “sides” of the angle.

Two rays, A B and A C make an acute angle. A point, C is marked on the ray, A B. An arrow from A B points to A C.

Figure 10.27 Vertex and Sides of an Angle

Classifying Angles

Angles are measured in radians or degrees. For example, an angle that measures $π$ radians, or 3.14159 radians, is equal to the angle measuring $180^{\circ} .$ An angle measuring $\frac{π}{2}$ radians, or 1.570796 radians, measures $90^{\circ} .$ To translate degrees to radians, we multiply the angle measure in degrees by $\frac{π}{180} .$ For example, to write $45^{\circ}$ in radians, we have

$45^{\circ} (\frac{π}{180}) = \frac{π}{4} = 0.785398 radians.$

To translate radians to degrees, we multiply by $\frac{180}{π} .$ For example, to write $2 π$ radians in degrees, we have

$2 π (\frac{180}{π}) = 360^{\circ} .$

Another example of translating radians to degrees and degrees to radians is $\frac{2 π}{3} .$ To write in degrees, we have $\frac{2 π}{3} (\frac{180}{π}) = 120^{\circ} .$ To write $30^{\circ}$ in radians, we have $30^{\circ} (\frac{π}{180}) = \frac{π}{6}$ . However, we will use degrees throughout this chapter.

FORMULA

To translate an angle measured in degrees to radians, multiply by $\frac{π}{180} .$

To translate an angle measured in radians to degrees, multiply by $\frac{180}{π} .$

Several angles are referred to so often that they have been given special names. A straight angle measures $180^{\circ} Figure 10.28.$

Four angles are depicted. Straight angle: 180 degrees. Right angle: 90 degrees. Acute angle: 60 degrees. Obtuse angle: 135 degrees.

Figure 10.28 Classifying and Naming Angles

An easy way to measure angles is with a protractor (Figure 10.29). A protractor is a very handy little tool, usually made of transparent plastic, like the one shown here.

A protractor with its center labeled and an inch ruler is across the bottom.

Figure 10.29 Protractor (credit: modification of work “School drawing tools” by Marco Verch/Flickr, CC BY 2.0)

With a protractor, you line up the straight bottom with the horizontal straight line of the angle. Be sure to have the center hole lined up with the vertex of the angle. Then, look for the mark on the protractor where the second ray lines up. As you can see from the image, the degrees are marked off. Where the second ray lines up is the measurement of the angle.

Checkpoint

Make sure you correctly match the center mark of the protractor with the vertex of the angle to be measured. Otherwise, you will not get the correct measurement. Also, keep the protractor in a vertical position.

Notation

Naming angles can be done in couple of ways. We can name the angle by three points, one point on each of the sides and the vertex point in the middle, or we can name it by the vertex point alone. Also, we can use the symbols $∠ Figure 10.30.$

Two rays, A C and A B make an acute angle.

Figure 10.30 Naming an Angle

We can name this angle $∡ B A C$ , or $∡ C A B$ , or $∡ A .$

Example 10.7

Classifying Angles

Determine which angles are acute, right, obtuse, or straight on the graph (Figure 10.31). You may want to use a protractor for this one.

Eight rays are graphed on a square grid. All the rays originate from the same point, O. The rays, O L and O E are horizontal. The ray, O H is vertical. The ray, O K makes an acute angle with O L. The ray, O J makes an acute angle with O K. The rays, O J and O H make an acute angle. The ray, O G makes an acute angle with O H. The ray, O F makes an acute angle with O G. The rays, O E and O F make an acute angle. The eighth ray is perpendicular to O F and O A.

Figure 10.31

Answer

Acute angles measure less than $90^{\circ} .$	Obtuse angles measure between $90^{\circ}$ and $180^{\circ} .$	Right angles measure $90^{\circ} .$	Straight angles measure $180^{\circ} .$
$\begin{array}{l} ∠ E O F \\ ∠ E O G \\ ∠ F O G \\ ∠ G O H \\ ∠ F O H \\ ∠ H O J \\ ∠ H O K \\ ∠ J O K \\ ∠ K O L \\ ∠ J O L \end{array}$	$\begin{array}{l} ∠ E O J \\ ∠ E O K \\ ∠ F O J \\ ∠ F O K \\ ∠ F O L \\ ∠ G O K \\ ∠ G O L \end{array}$	$\begin{array}{l} ∠ E O H \\ ∠ H O L \\ ∠ G O J \end{array}$	$∠ E O L$

Most angles can be classified visually or by description. However, if you are unsure, use a protractor.

Your Turn 10.7

Determine which angles are acute, obtuse, right, and straight in the graph.

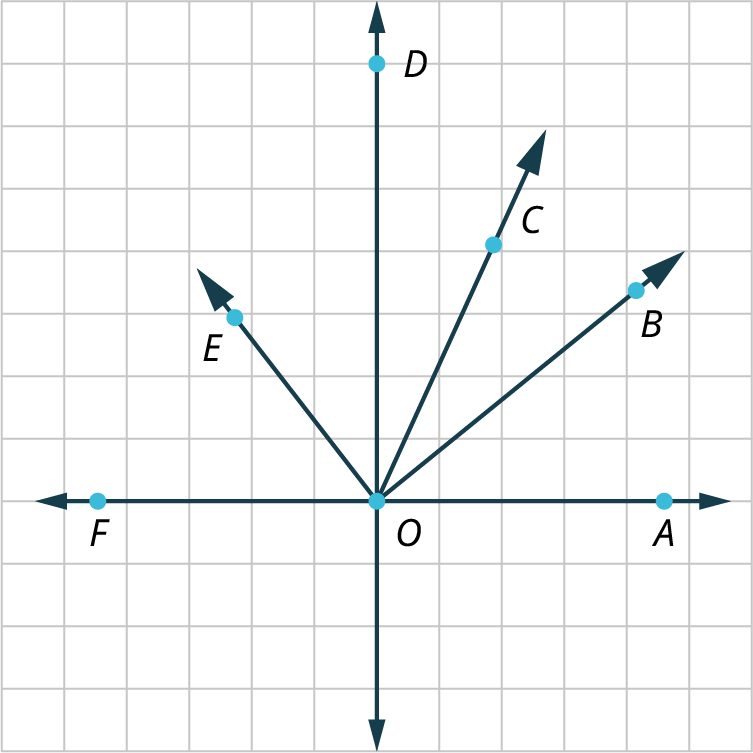
Seven rays are graphed on a squared grid. All the rays originate from the same point, O. The rays, O F and O A are horizontal. The ray, O D is vertical. The ray, O E makes an acute angle with O F. The ray, O E makes an acute angle with O D. The ray, O C makes an acute angle with O D. The ray, O B makes an acute angle with O C. The rays, O B, and O A make an acute angle. The seventh ray is perpendicular to O F and O A.

Figure 10.32

Adjacent Angles

Two angles with the same starting point or vertex and one common side are called adjacent angles. In Figure 10.33, angle $∠ D B C$ is adjacent to $∠ C B A$ . Notice that the way we designate an angle is with a point on each of its two sides and the vertex in the middle.

Three rays, B A, B C, and B D originate from the same point, B. The rays, B A, and B C make an acute angle. The rays, B C, and B D make an acute angle. The angle, A B D is acute.

Figure 10.33 Adjacent Angles

Supplementary Angles

Two angles are supplementary if the sum of their measures equals $180^{\circ} . Figure 10.34, we are given that m ∡ F B E = 35^{\circ}, so what is m ∡ A B E ? These are supplementary angles. Therefore, because m ∡ A B F = 180^{\circ}, and as 180^{\circ} - 35^{\circ} = 145^{\circ}, we have m ∡ A B E = 145^{\circ} .$

Five rays originate from the same point, B. The rays, B F, and B A are horizontal. The ray, B D is vertical. The ray, B E lies between B F and B D and it makes an acute angle with each ray. The ray, B C lies between B D and B A, and it makes an acute angle with each ray.

Figure 10.34 Supplementary Angles

Example 10.8

Solving for Angle Measurements and Supplementary Angles

Solve for the angle measurements in Figure 10.35.

A horizontal line with a ray originating from its center. The line makes an acute angle, 5 x plus 2 with the ray, and an obtuse angle, 32 x minus 7 with the ray.

Figure 10.35

Answer

Step 1: These are supplementary angles. We can see this because the two angles are part of a horizontal line, and a horizontal line represents $180^{\circ} .$ Therefore, the sum of the two angles equals $180^{\circ} .$

Step 2:

$\begin{matrix} (32 x - 7) + (5 x + 2) & = & 180 \\ 37 x - 5 & = & 180 \\ 37 x & = & 185 \\ x & = & 5 \end{matrix}$

Step 3: Find the measure of each angle:

$\begin{matrix} 32 x - 7 & = & 32 (5) - 7 \\ = & 153^{\circ} \\ 5 x + 2 & = & 5 (5) + 2 \\ = & 27^{\circ} \end{matrix}$

Step 4: We check: $153^{\circ} + 27^{\circ} = 180^{\circ} .$

Your Turn 10.8

Solve for the angle measurements in the figure shown.

A horizontal line with a ray originating from its center. The line makes an acute angle, 2 x plus 5 with the ray, and an obtuse angle, 5 x with the ray.

Figure 10.36

Complementary Angles

Two angles are complementary if the sum of their measures equals $90^{\circ} . Figure 10.37, we have m ∡ A B C = 30^{\circ}, and m ∡ A B D = 90^{\circ} . What is the m ∡ C B D ? These are complementary angles. Therefore, because 90^{\circ} - 30^{\circ} = 60^{\circ}, the ∡ C B D = 60^{°} .$

Two lines, A B and B D intersect each other forming a right angle. A ray, B C makes an acute angle, 6 x minus 5 with the line, B A. Another ray originating from B makes an acute angle, 9 x with the line, B D. This ray and B C make an acute angle of 20 degrees.

Figure 10.37 Complementary Angles

Example 10.9

Solving for Angle Measurements and Complementary Angles

Solve for the angle measurements in Figure 10.38.

Two lines intersect each other forming a right angle. A ray makes an acute angle, 7 x minus 5 with the horizontal line. Another ray originating from the intersection point of the lines makes an acute angle, 9 x minus 5 with the vertical line. An acute angle of 4 x is formed by these two rays.

Figure 10.38

Answer

We have that

$\begin{matrix} (9 x - 5) + 4 x + (7 x - 5) & = & 90 \\ 20 x & = & 100 \\ x & = & 5 \end{matrix}$

Then, $m ∡ (9 x - 5) = 40^{\circ}$ , $m ∡ (4 x) = 20^{\circ}$ , and $m ∡ (7 x - 5) = 30^{\circ} .$

Your Turn 10.9

Find the measure of each angle in the illustration.

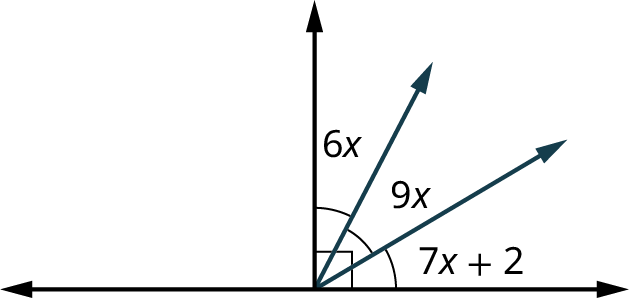
Two lines intersect each other forming a right angle. A ray makes an acute angle, 7 x plus 2 with the horizontal line. Another ray originating from the intersection point of the lines makes an acute angle, 6 x with the vertical line. An acute angle of 9 x is formed by these two rays.

Figure 10.39

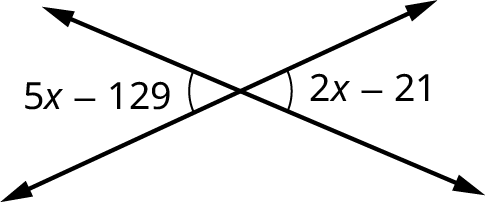
Vertical Angles

When two lines intersect, the opposite angles are called vertical angles, and vertical angles have equal measure. For example, Figure 10.40 shows two straight lines intersecting each other. One set of opposite angles shows angle markers; those angles have the same measure. The other two opposite angles have the same measure as well.

Two lines intersect each other. One set of opposite angles is shaded.

Figure 10.40 Vertical Angles

Example 10.10

Calculating Vertical Angles

In Figure 10.41, one angle measures $40^{\circ} .$ Find the measures of the remaining angles.

Two lines intersect each other. One set of opposite angles is labeled 1 and 3. The other set of opposite angles is labeled 2 and 40 degrees.

Figure 10.41

Answer

The 40-degree angle and $∠ 2$ are vertical angles. Therefore, $m ∡ 2 = 40^{\circ} .$

Notice that $∡ 2$ and $∡ 1$ are supplementary angles, meaning that the sum of $m ∡ 2$ and $m ∡ 1$ equals $180^{\circ} .$ Therefore, $m ∡ 1 = 180^{\circ} - 40^{\circ} = 140^{\circ}$ .

Since $∡ 1$ and $∡ 3$ are vertical angles, then $m ∡ 3$ equals $140^{\circ} .$

Your Turn 10.10

Given the two intersecting lines in the figure shown and /**/m\measuredangle 2 = {67^ \circ },/**/ find the measure of the remaining angles.

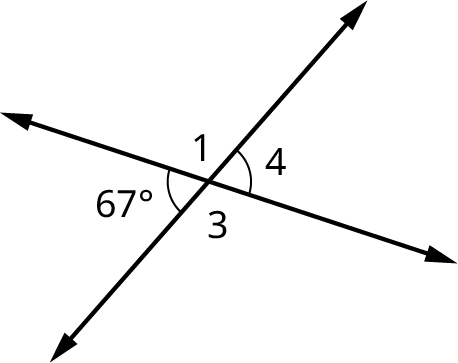
Two lines intersect each other. One set of opposite angles is labeled 1 and 3. The other set of opposite angles is labeled 4 and 67 degrees.

Figure 10.42

Transversals

When two parallel lines are crossed by a straight line or transversal, eight angles are formed, including alternate interior angles, alternate exterior angles, corresponding angles, vertical angles, and supplementary angles. See Figure 10.43. Angles 1, 2, 7, and 8 are called exterior angles, and angles 3, 4, 5, and 6 are called interior angles.

Two parallel lines, l subscript 1 and l subscript 2 are intersected by a transversal. The transversal makes four angles numbered 1, 2, 3, and 4 with the line, l subscript 1. The transversal makes four angles numbered 5, 6, 7, and 8 with the line, l subscript 2. 1, 2, 7, and 8 are exterior angles. 3, 4, 5, and 6 are interior angles.

Figure 10.43 Transversal

Alternate Interior Angles

Alternate interior angles are the interior angles on opposite sides of the transversal. These two angles have the same measure. For example, $∡ 3 Figure 10.44.$

Figure 10.44 Alternate Interior Angles

Alternate Exterior Angles

Alternate exterior angles are exterior angles on opposite sides of the transversal and have the same measure. For example, in Figure 10.45, $∡ 2$ and $∡ 7$ are alternate exterior angles and have equal measures; $∡ 1$ and $∡ 8$ are alternate exterior angles and have equal measures as well.

Figure 10.45 Alternate Exterior Angles

Corresponding Angles

Corresponding angles refer to one exterior angle and one interior angle on the same side as the transversal, which have equal measures. In Figure 10.46, $∡ 1$ and $∡ 5$ are corresponding angles and have equal measures; $∡ 3$ and $∡ 7$ are corresponding angles and have equal measures; $∡ 2$ and $∡ 6$ are corresponding angles and have equal measures; $∡ 4$ and $∡ 8$ are corresponding angles and have equal measures as well.

Figure 10.46 Corresponding Angles

Example 10.11

Evaluating Space

You live on the corner of First Avenue and Linton Street. You want to plant a garden in the far corner of your property (Figure 10.47) and fence off the area. However, the corner of your property does not form the traditional right angle. You learned from the city that the streets cross at an angle equal to $150^{\circ} .$ What is the measure of the angle that will border your garden?

Two streets, First Avenue and Linton Street intersect each other. One set of opposite angles is unknown and 150 degrees. The other set of opposite angles shows the garden on the left and blank on the right.

Figure 10.47

Answer

As the angle between Linton Street and First Avenue is $150^{\circ},$ the supplementary angle is $30^{\circ} .$ Therefore, the garden will form a $30^{\circ}$ angle at the corner of your property.

Your Turn 10.11

Suppose you have a similar property to the one in Figure 10.53, but the angle that corresponds to the garden corner is /**/{50^ \circ }/**/. What is the measure between the two cross streets?

Example 10.12

Determining Angles Formed by a Transversal

In Figure 10.48 given that angle 3 measures $40^{\circ},$ find the measures of the remaining angles and give a reason for your solution.

Two parallel lines, l subscript 1 and l subscript 2 are intersected by a transversal. The transversal makes four angles numbered 1, 2, 40 degrees, and 4 with the line, l subscript 1. The transversal makes four angles numbered 5, 6, 7, and 8 with the line, l subscript 2. 1, 2, 7, and 8 are exterior angles. 40 degrees, 4, 5, and 6 are interior angles. The corresponding angles, 1 and 5 are highlighted.

Figure 10.48

Answer

$m ∡ 2 = m ∡ 3 = 40^{\circ}$ by vertical angles.

$∡ 3 = m ∡ 7$ by corresponding angles.

$m ∡ 7 = m ∡ 6 = 40^{\circ}$ by vertical angles.

$m ∡ 1 = 180 - 40 = 140^{\circ}$ by supplementary angles.

$m ∡ 4 = m ∡ 1 = 140^{\circ}$ by vertical angles.

$m ∡ 8 = m ∡ 1 = 140^{\circ}$ by alternate exterior angles.

$m ∡ 5 = m ∡ 8 = 140^{\circ}$ by vertical angles.

Your Turn 10.12

In the given figure if /**/m\measuredangle 1 = {120^ \circ }/**/, find the /**/m\measuredangle 5/**/, /**/m\measuredangle 4/**/, and /**/m\measuredangle 8/**/.

Figure 10.49

Example 10.13

Measuring Angles Formed by a Transversal

In Figure 10.50 given that angle 2 measures $23^{\circ},$ find the measure of the remaining angles and state the reason for your solution.

Two parallel lines, l subscript 1 and l subscript 2 are intersected by a transversal. The transversal makes four angles numbered 1, 23 degrees, 3, and 4 with the line, l subscript 1. The transversal makes four angles numbered 5, 6, 7, and 8 with the line, l subscript 2. 1, 23 degrees, 7, and 8 are exterior angles. 3, 4, 5, and 6 are interior angles. The corresponding angles, 1 and 5 are highlighted.

Figure 10.50

Answer

$m ∡ 2 = m ∡ 3 = 23^{\circ}$ by vertical angles, because $∡ 2$ and $∡ 3$ are the opposite angles formed by two intersecting lines.

$m ∡ 1 = 157^{\circ}$ by supplementary angles to $m ∡ 2$ or $m ∡ 3.$ We see that $∡ 1$ and $∡ 2$ form a straight angle as does $∡ 1$ and $∡ 3.$ A straight angle measures $180^{\circ},$ so $180^{\circ} - 23^{\circ} = 157^{\circ} .$

$m ∡ 4 = m ∡ 1 = 157^{\circ}$ by vertical angles, because $∡ 4$ and $∡ 1$ are the two opposite angles formed by two intersecting lines.

$m ∡ 5 = m ∡ 1 = 157^{\circ}$ by corresponding angles because they are the same angle formed by the transversal crossing two parallel lines, one exterior and one interior.

$m ∡ 8 = m ∡ 5 = 157^{\circ}$ by vertical angles because $∡ 8$ and $∡ 5$ are the two opposite angles formed by two intersecting lines.

$m ∡ 7 = m ∡ 2 = 23^{\circ}$ by alternate exterior angles because, like vertical angles, these angles are the opposite angles formed by the transversal intersecting two parallel lines.

$m ∡ 6 = m ∡ 7 = 23^{\circ}$ by vertical angles because these are the opposite angles formed by two intersecting lines.

Your Turn 10.13

In the provided figure given that the /**/m\measuredangle 2 = {48^ \circ }/**/, find /**/m\measuredangle 1/**/, and /**/m\measuredangle 5./**/

Figure 10.51

Example 10.14

Finding Missing Angles

Find the measures of the angles 1, 2, 4, 11, 12, and 14 in Figure 10.52 and the reason for your answer given that $l_{1}$ and $l_{2}$ are parallel.

Two parallel lines, l subscript 1 and l subscript 2 are intersected by two transversals. The first transversal makes four angles numbered 62 degrees, 9, 7, and 8 with the line, l subscript 2. The second transversal makes four angles numbered 14, 62 degrees, 11, and 12 with the line, l subscript 2. The two transversals intersect at a point on the line, l subscript 1. Six angles are formed around the intersection point. The angles are labeled 1, 2, 62 degrees, 4, 5, and 6.

Figure 10.52

Answer

$m ∡ 12 = 118^{\circ}$ , supplementary angles

$m ∡ 14 = 118^{\circ}$ , vertical angles

$m ∡ 11 = 62^{\circ}$ , vertical angles

$m ∡ 4 = 62^{\circ}$ , corresponding angles

$m ∡ 1 = 62^{\circ}$ , vertical angles

$m ∡ 2 = 56^{\circ}$ , supplementary angles

Your Turn 10.14

Using Figure 10.58, find the measures of angles 5, 6, 7, 8, and 9.

Who Knew?

The Number 360

Did you ever wonder why there are $360^{\circ}$ in a circle? Why not $100^{\circ}$ or $500^{\circ} ?$ The number 360 was chosen by Babylonian astronomers before the ancient Greeks as the number to represent how many degrees in one complete rotation around a circle. It is said that they chose 360 for a couple of reasons: It is close to the number of days in a year, and 360 is divisible by 2, 3, 4, 5, 6, 8, 9, 10, …

Check Your Understanding

Classify the following angles as acute, right, obtuse, or straight.

10.

/**/m\measuredangle = {180^ \circ }/**/

11.

/**/m\measuredangle = {176^ \circ }/**/

12.

/**/m\measuredangle = {90^ \circ }/**/

13.

/**/m\measuredangle = {37^ \circ }/**/

For the following exercises, determine the measure of the angles in the given figure.
$Two parallel lines, l subscript 1 and l subscript 2 are intersected by a transversal. The transversal makes four angles labeled 1, 31 degrees, 3, and 4 with the line, l subscript 1. The transversal makes four angles numbered 5, 6, 7, and 8 with the line, l subscript 2. 1, 31 degrees, 7, and 8 are exterior angles. 3, 4, 5, and 6 are interior angles.$

14.

Find the measure of /**/\measuredangle 1/**/ and state the reason for your solution.

15.

Find the measure of /**/\measuredangle 3/**/ and state the reason for your solution.

16.

Find the measure of /**/\measuredangle 5/**/ and state the reason for your solution.

Section 10.2 Exercises

Classify the angles in the following exercises as acute, obtuse, right, or straight.

/**/m\measuredangle = {32^ \circ }/**/

/**/m\measuredangle = {120^ \circ }/**/

/**/m\measuredangle = {180^ \circ }/**/

/**/m\measuredangle = {90^ \circ }/**/

/**/m\measuredangle = {110^ \circ }/**/

/**/m\measuredangle = {45^ \circ }/**/

Use the given figure to solve for the angle measurements.
$Two lines intersect each other forming a right angle. A ray originates from the intersection point of the lines. The ray makes an acute angle, 5 x plus 4 with the horizontal line. The ray makes an acute angle, 39 x minus 2 with the vertical line.$

Use the given figure to solve for the angle measurements.
$A horizontal line with two rays originating from its center. The first ray makes an angle, 3 x plus 2 with the horizontal axis. The angle formed between the two rays is labeled 3 x plus 7. The second ray makes an angle, 2 x plus 3 with the horizontal axis.$

Give the measure of the supplement to /**/{89^ \circ }./**/

Use the given figure for the following exercises. Let angle 2 measure /**/{35^ \circ }/**/.
$Two parallel lines, l subscript 1 and l subscript 2 are intersected by a transversal. The transversal makes four angles numbered 1, 2, 3, and 4 with the line, l subscript 1. The transversal makes four angles numbered 5, 6, 7, and 8 with the line, l subscript 2. 1, 2, 7, and 8 are exterior angles. 3, 4, 5, and 6 are interior angles.$

10.

Find the measure of angle 1 and state the reason for your solution.

11.

Find the measure of angle 3 and state the reason for your solution.

12.

Find the measure of angle 4 and state the reason for your solution.

13.

Find the measure of angle 5 and state the reason for your solution.

14.

Find the measure of angle 6 and state the reason and state the reason for your solution.

15.

Find the measure of angle 7 and state the reason for your solution.

16.

Find the measure of angle 8 and state the reason for your solution.

17.

Use the given figure to solve for the angle measurements.
$Two lines intersect each other. One set of opposite angles is labeled 5 x minus 129 and 2 x minus 21.$

Use the given figure for the following exercises.
$Two parallel lines are intersected by a transversal. The transversal makes four angles with the line, l subscript 1. Two angles are unknown. Two opposite angles are marked 3 and 50 degrees. The transversal makes four angles with the line, l subscript 2. 8 and 50 degrees are exterior angles. 3 is the interior angle.$

18.

Find the measure of angle 3 and explain the reason for your solution.

19.

Find the measure of angle 8 and explain the reason for your solution.