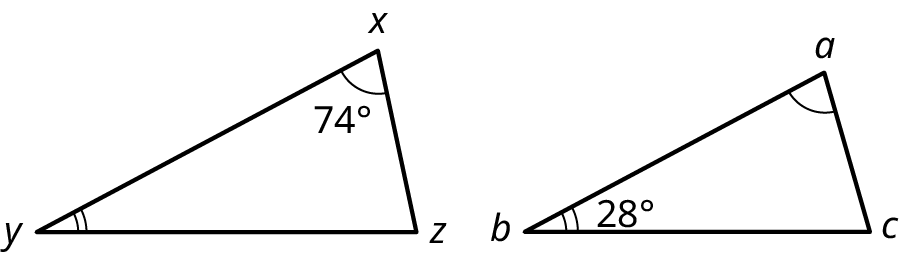10.4: Triangles

Figure 10.53 The appearance of triangles in buildings is part of modern-day architectural design. (credit: "Inside Hallgrímskirkja church, Reykjavik, Iceland" by O Palsson/Flickr, CC BY 2.0)

Learning Objectives

After completing this section, you should be able to:

1. Identify triangles by their sides.
2. Identify triangles by their angles.
3. Determine if triangles are congruent.
4. Determine if triangles are similar.
5. Find the missing side of similar triangles.

How were the ancient Greeks able to calculate the radius of Earth? How did soldiers gauge their target? How was it possible centuries ago to estimate the height of a sail at sea? Triangles have always played a significant role in how we find heights of objects too high to measure or distances between objects too far away to calculate. In particular, the concept of similar triangles has countless applications in the real world, and we shall explore some of those applications in this section.

Technology has given us instruments that allow us to find measurements of distant objects with little effort. However, it is all based on the properties of triangles discovered centuries ago. In this section, we will explore the various types of triangles and their special properties, as well as how to measure interior and exterior angles. We will also explore congruence theorems and similarity.

Identifying Triangles

Joining any three noncollinear points with line segments produces a triangle. For example, given points $A$

Figure 10.54 Triangle

Triangles are classified by their angles and their sides. All angles in an acute triangle measure $<{90}^{\circ }.$

A few other facts to remember as we move forward:

• The points where the line segments meet are called the vertices (plural for vertex).
• We often refer to sides of a triangle by the angle they are opposite. In other words, side $a$ is opposite angle $A$, side $b$ is opposite angle $B$, and side $c$ is opposite angle $C$.

Figure 10.55 Types of Triangles

We want to add a special note about right triangles here, as they are referred to more than any other triangle. The side opposite the right angle is its longest side and is called the hypotenuse, and the sides adjacent to the right angle are called the legs.

One of the most important properties of triangles is that the sum of the interior angles equals ${180}^{\circ }.$

Figure 10.56 Sum of Interior Angles

This is how the proof goes:

Step 1: Start with a straight line $\overleftrightarrow{AB}$ and a point $C$ not on the line.

Step 2: Draw a line through point $C$ parallel to the line $\overleftrightarrow{AB}$.

Step 3: Construct two transversals (a line crossing the parallel lines), one angled to the right and one angled to the left, to intersect the parallel lines.

Step 4: Because of the property that alternate interior angles inside parallel lines are equal, we have that

$$m\measuredangle 2=m\sphericalangle 1\text{and}m\measuredangle 3=m\measuredangle 4.$$

Step 5: Notice that $m\measuredangle 2+m\measuredangle 5+m\measuredangle 4={180}^{\circ }$ by the straight angle property.

Step 6: Therefore, by substitution, $m\measuredangle 1=m\measuredangle 2,$ and $m\measuredangle 3=m\measuredangle 4,$ we have that

$$m\measuredangle 1+m\measuredangle 3+m\sphericalangle 5={180}^{\circ }\text{.}$$

Therefore, the sum of the interior angles of a $\text{triangle}={180}^{\circ }.$

Example 10.15

Finding Measures of Angles Inside a Triangle

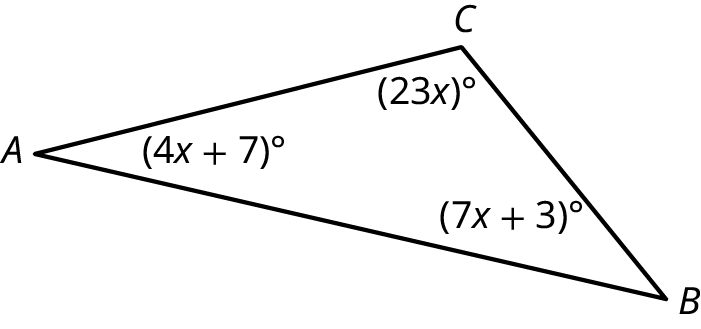
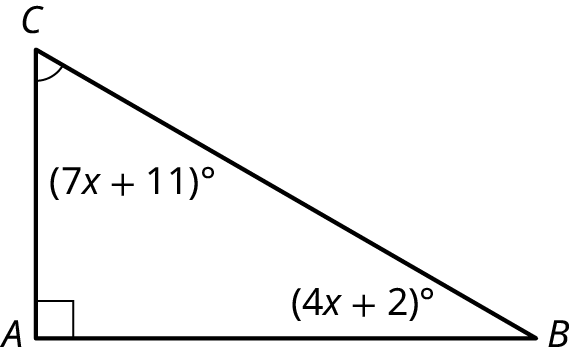
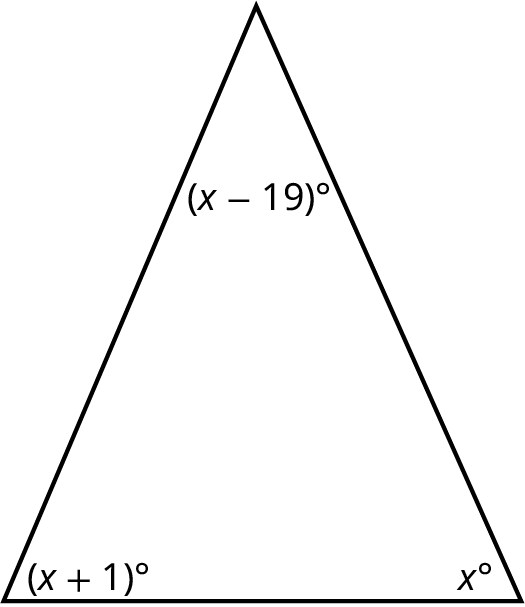
Find the measure of each angle in the triangle shown (Figure 10.57). We know that the sum of the angles must equal ${180}^{\circ }.$

Figure 10.57

Answer

Step 1: As the sum of the interior angles equals ${180}^{\circ },$ we can use algebra to find the measures:

$$\begin{array}{ccc}\hfill x+(x+17)+(3x-62)& \hfill =\hfill & 180\hfill \\ \hfill 5x-45& \hfill =\hfill & 180\hfill \\ \hfill 5x& \hfill =\hfill & 225\hfill \\ \hfill x& \hfill =\hfill & \frac{225}{5}=45\hfill \end{array}$$

Step 2: Now that we have the value of $x$, we can substitute 45 into the other two expressions to find the measure of those angles:

$$\begin{array}{ccc}\hfill \left(x+17\right)& \hfill =\hfill & 45+17={62}^{\circ }\hfill \\ \hfill (3x-62)& \hfill =\hfill & 3(45)-62=135-62={73}^{\circ }\hfill \end{array}$$

Step 3: Then, $m\measuredangle x={45}^{\circ }$, $m\measuredangle (x+17)={62}^{\circ }$, and $m\measuredangle (3x-62)={73}^{\circ }.$

Your Turn 10.15

1.

Find the measures of each angle in the triangle shown.

Figure 10.58

Example 10.16

Finding Angle Measures

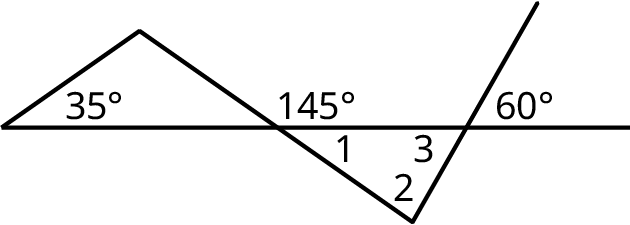
Find the measure of angles numbered 1–5 in Figure 10.59.

Figure 10.59

Answer

The $m\measuredangle 1={119}^{\circ }$ because it is supplementary with the unknown angle of the adjacent triangle. The unknown angle measures ${61}^{\circ }.$ The $m\measuredangle 2={61}^{\circ }$ because of vertical angles. The $m\measuredangle 5={59}^{\circ }$ because the angle that is supplementary to the ${134}^{\circ }$ measures ${46}^{\circ }$, and angle 5 is the unknown angle in that triangle. The $m\measuredangle 4={59}^{\circ }$ by vertical angles. Finally, $m\measuredangle 3={60}^{\circ },$ as it is the third angle in the triangle with angles measuring ${59}^{\circ }$ and ${61}^{\circ }.$

Your Turn 10.16

1.

Find the measure of angles 1, 2, and 3 in the figure shown.

Figure 10.60

Congruence

If two triangles have equal angles and their sides lengths are equal, the triangles are congruent. In other words, if you can pick up one triangle and place it on top of the other triangle and they coincide, even if you have to rotate one, they are congruent.

Example 10.17

Determining If Triangles Are Congruent

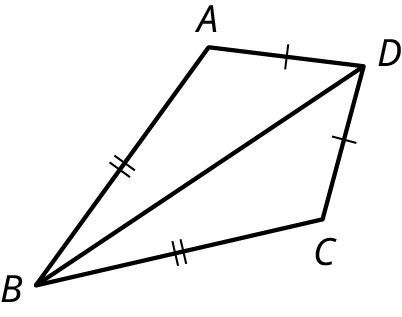
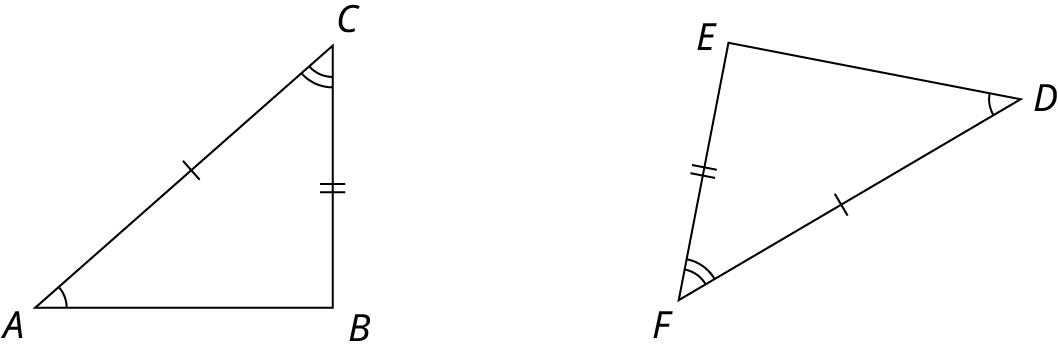
In Figure 10.61, is the triangle $\mathit{ABC}$ congruent to triangle $\mathit{DEF}$?

Figure 10.61

Answer

Triangle $\mathit{ABC}$ is congruent to triangle $\mathit{DEF}$. Angles $A$ and $C$ are congruent to angles $D$ and $F$, which implies that angle $B$ is congruent to angle $E$. Side $\mathit{AB}$ is congruent to side $\mathit{DE}$, and side $\mathit{CB}$ is congruent to side $\mathit{FE}$, which implies that side $\mathit{AC}$ is congruent to side $\mathit{DF}$.

Your Turn 10.17

1.

In the figure shown, is triangle /**/ABC/**/ congruent to triangle /**/DEF/**/?

Figure 10.62

The Congruence Theorems

The following theorems are tools you can use to prove that two triangles are congruent. We use the symbol $\cong$ to define congruence. For example, $\text{Δ}ABC\cong \text{Δ}DEF$.

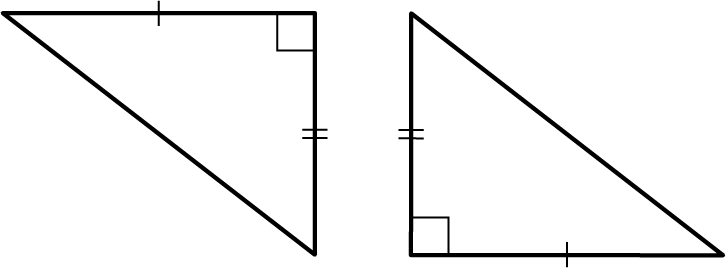
Side-Side-Side (SSS). If three sides of one triangle are equal to the corresponding sides of the second triangle, then the triangles are congruent. See Figure 10.63.

Figure 10.63 Side-Side-Side (SSS)

We have that $\overline{DF}\cong \overline{RT}$, $\overline{EF}\cong \overline{ST},$ and $\overline{\mathit{DE}}\cong \overline{\mathit{RS}}\text{,}$ then $\text{Δ}DEF\cong \text{Δ}RST.$

Side-Angle-Side (SAS). If two sides of a triangle and the angle between them are equal to the corresponding two sides and included angle of the second triangle, then the triangles are congruent. See Figure 10.64. We see that $\overline{AB}\cong \overline{A^{\prime }{B}^{\prime }}$ and $\overline{BC}\cong \overline{B^{\prime }{C}^{\prime }}$, $m\measuredangle B=m\measuredangle B^{\prime }$, then $\text{Δ}ABC\cong \text{Δ}{A}^{\prime }{B}^{\prime }{C}^{\prime }$.

Figure 10.64 Side-Angle-Side (SAS)

Angle-Side-Angle (ASA). If two angles and the side between them in one triangle are congruent to the two corresponding angles and the side between them in a second triangle, then the two triangles are congruent. See Figure 10.65. Notice that $m\measuredangle \text{A}\cong m\measuredangle \text{F}$, and $m\measuredangle \text{C}\cong m\measuredangle \text{D}$, $\overline{\mathit{AC}}\cong \overline{\mathit{DF}}$, then $\text{Δ}\mathit{ABC}\cong \text{Δ}\mathit{DEF}.$

Figure 10.65 Angle-Side-Angle (ASA)

Angle-Angle-Side (AAS). If two angles and a nonincluded side of one triangle are congruent to two angles and the nonincluded corresponding side of a second triangle, then the triangles are congruent.

See Figure 10.66. We see that $m\measuredangle X\cong m{X}^{\prime }$, $m\measuredangle Z\cong m\measuredangle Z^{\prime }$, and $\overline{XY}\cong \overline{X^{\prime }{Y}^{\prime }}$, then $\text{Δ}XYZ\cong \text{Δ}{X}^{\prime }{Y}^{\prime }{Z}^{\prime }$.

Figure 10.66 Angle-Angle-Side (AAS)

Example 10.18

Identifying Congruence Theorems

What congruence theorem is illustrated in Figure 10.67?

Figure 10.67

Answer

AAS: Two angles and a non-included side in one triangle are congruent to the corresponding angles and side in the second triangle.

Your Turn 10.18

1.

Identify the congruence theorem being illustrated in the figure shown.

Figure 10.68

Example 10.19

Determining the Congruence Theorem

What congruence theorem is illustrated in Figure 10.69?

Figure 10.69

Answer

The SSS theorem.

Your Turn 10.19

1.

What congruence theorem is being illustrated in the figure shown?

Figure 10.70

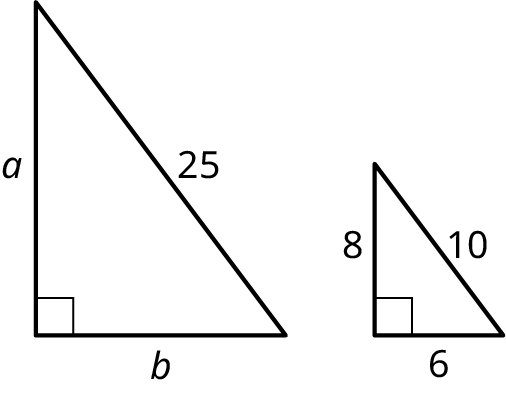
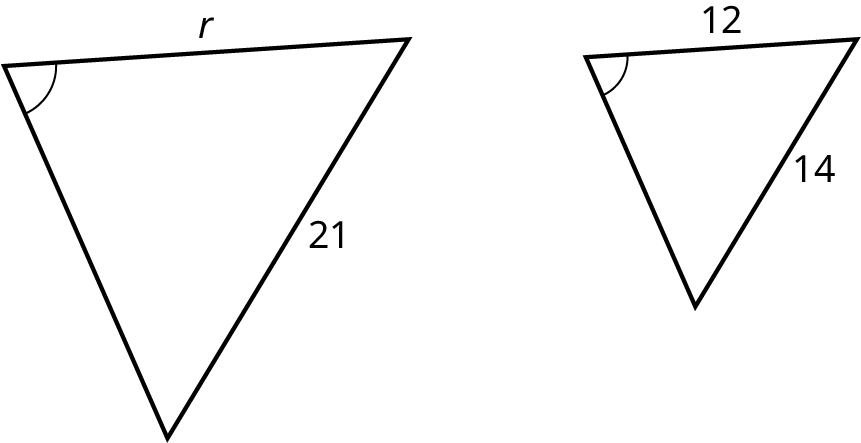
Similarity

If two triangles have the same angle measurements and are the same shape but differ in size, the two triangles are similar. The lengths of the sides of one triangle will be proportional to the corresponding sides of the second triangle. Note that a single fraction $\frac{a}{b}$ is called a ratio, but two fractions equal to each other is called a proportion, such as $\frac{a}{b}=\frac{c}{d}.$

This rule of similarity applies to all shapes as well as triangles. Another way to view similarity is by applying a scaling factor, which is the ratio of corresponding measurements between an object or representation of the object, to an image that produces the second, similar image.

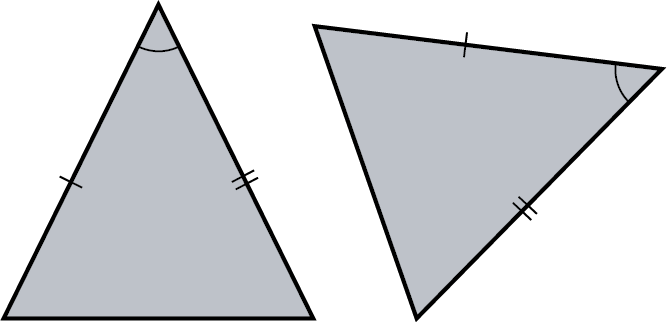
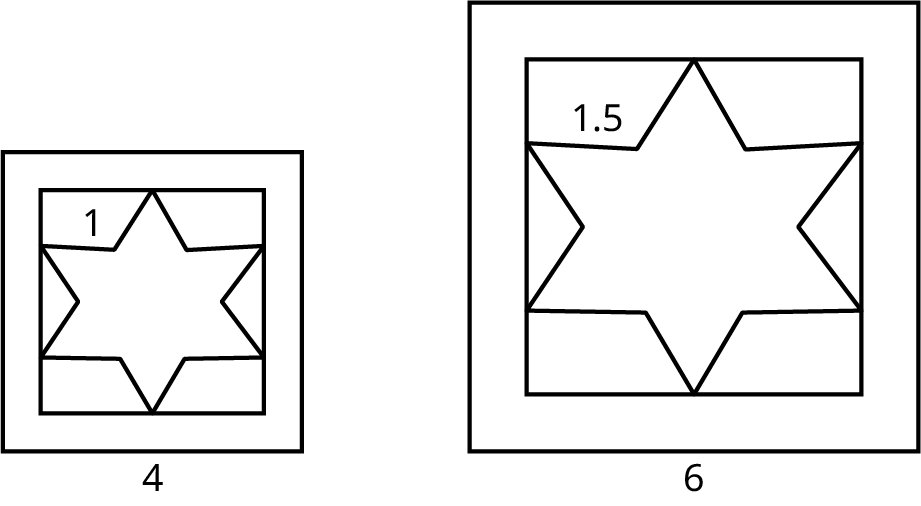
For example, why are the two images in Figure 10.71 are similar? These two images have the same proportions between elements. Therefore, they are similar.

Figure 10.71 Similarity

Example 10.20

Determining If Triangles Are Similar

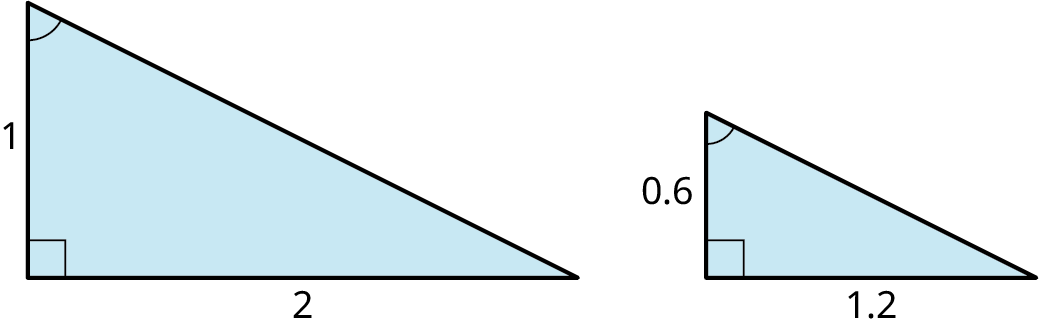
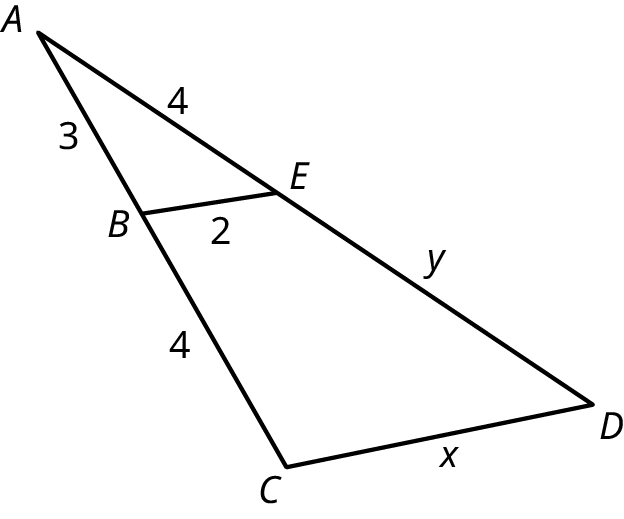
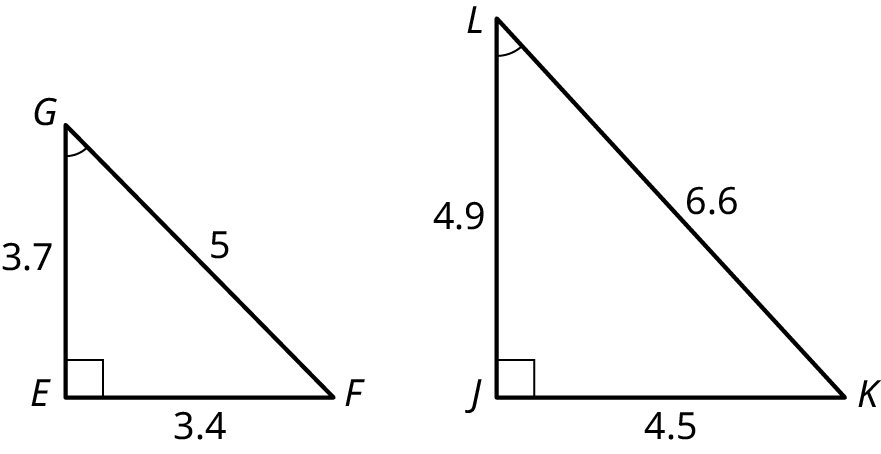
Are the two triangles shown in Figure 10.72 similar?

Figure 10.72

Answer

Step 1: We will look at the proportions within each triangle. In triangle $\alpha$ (alpha), the side opposite the ${57}^{\circ }$ angle measures 7, and the side opposite the ${33}^{\circ }$ angle measures 4. Then, the measures of the corresponding sides in triangle $\beta$ (beta) measures 3.5 and 2, respectively. We have

$$\frac{4}{7}=0.5714\frac{2}{3.5}=\mathrm{0.5714.}$$

This is the proportion $\frac{4}{7}=\frac{2}{3.5}$. The scaling factor is 0.5714.

Step 2: Let’s try another correspondence. In triangle $\alpha$, the hypotenuse measures 8.06 and the side opposite the ${57}^{\circ }$ angle measures 7. In triangle $\beta$, the hypotenuse measure 4.03 and the side opposite the ${57}^{\circ }$ angle measures 3.5. We have

$$\frac{7}{8.06}=0.8685\frac{3.5}{4.03}=\mathrm{0.8685.}$$

Step 3: Now, let’s look at the proportions between triangle $\alpha$ and triangle $\beta .$ The side measuring 2 in triangle $\beta$ corresponds to the side measuring 4 in triangle $\alpha$, the side measuring 3.5 in triangle $\beta$ corresponds to the side measuring 7 in triangle $\alpha ,$ and the hypotenuse in triangle $\beta$ corresponds to the hypotenuse in triangle $\alpha .$ We have

$$\frac{2}{4}=0.5\frac{3.5}{7}=0.5\frac{4.03}{8.06}=0.5$$

Thus, the corresponding angles are equal and the proportions between each pair of corresponding sides equals 0.5. In other words, the scaling factor is 0.5. Therefore, the triangles are similar.

Your Turn 10.20

1.

Is triangle /**/EFG/**/ similar to triangle /**/JKL/**/ in the figure shown?

Figure 10.73

Example 10.21

Proving Similarity

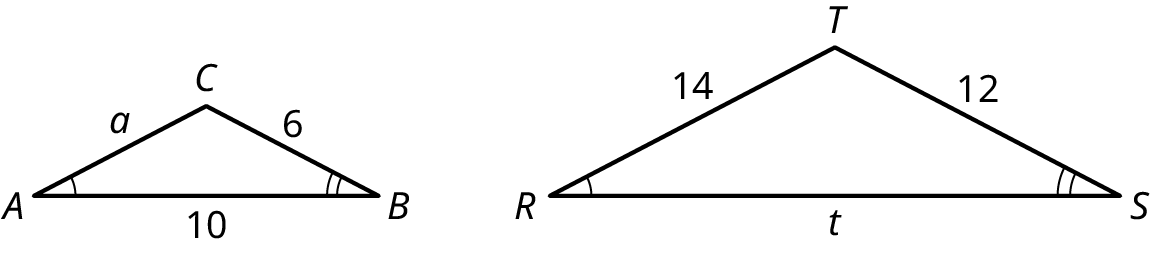
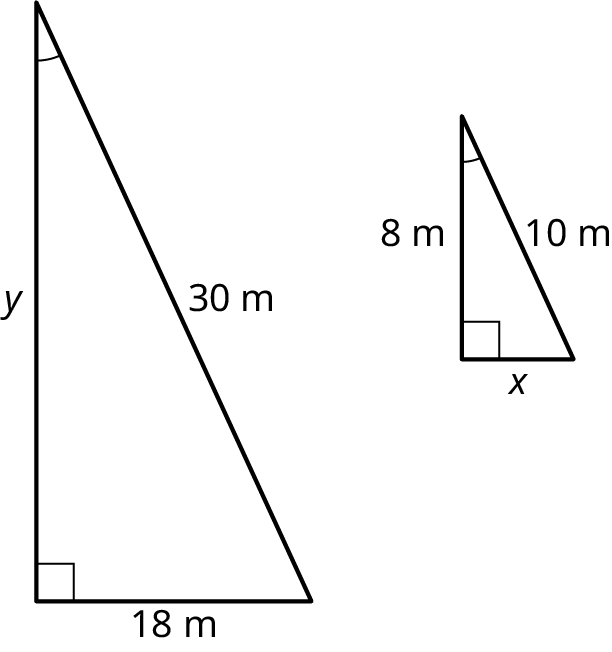
In Figure 10.74, is triangle $\delta$ (delta) similar to triangle $\epsilon$ (epsilon)? Find the lengths of sides $x$ and $y$ as part of your answer.

Figure 10.74

Answer

We can see that all three angles in triangle $\delta$ are equal to the corresponding angles in triangle $\epsilon$. That is enough to determine similarity. However, we want to find the values of $x$ and $y$ to prove similarity.

Step 1: We have to do is set up the proportions between the corresponding sides. We have the side that measures 2.375 in triangle $\delta$ corresponding to the side measuring 1.069 in triangle $\epsilon$. We have the hypotenuse/side in triangle $\delta$ measuring 6 corresponding to the hypotenuse/side labeled $y$ in triangle $\epsilon$. And, finally, the side labeled $x$ in triangle $\delta$ corresponds to the side measuring 2.475 in triangle $\epsilon .$

Each proportion should be equal. We start with the proportion of the shorter sides. Thus

$$\frac{1.069}{2.375}=0.45$$

Step 2: We solve for $y$ using the first proportion. Set the two ratios equal to each other, cross-multiply, and solve for $y$. We have:

$$\begin{array}{ccc}\hfill \frac{1.069}{2.375}& \hfill =\hfill & \frac{y}{6}\hfill \\ \hfill (6)(1.069)& \hfill =\hfill & (2.375)(y)\hfill \\ \hfill 6.414& \hfill =\hfill & 2.375y\hfill \\ \hfill \frac{6.414}{2.375}& \hfill =\hfill & 2.7=y\hfill \end{array}$$

So, $y=2.7$.

Step 3: Checking that length in the proportion factor of 0.45, we have:

$$\frac{y}{6}=\frac{2.7}{6}=0.45$$

Step 4: Solving for $x$, we will use the same proportion we used to solve for $y$. We have:

$$\begin{array}{ccc}\hfill \frac{1.069}{2.375}& \hfill =\hfill & \frac{2.475}{x}\hfill \\ \hfill 1.069(x)& \hfill =\hfill & 2.475(2.375)\hfill \\ \hfill 1.069(x)& \hfill =\hfill & 5.878\hfill \\ \hfill x& \hfill =\hfill & \frac{5.878}{1.069}=5.5\hfill \\ \hfill \frac{2.475}{x}& \hfill =\hfill & \frac{2.475}{5.5}=0.45\hfill \end{array}$$

Step 5: We test the proportions. We have the following:

$$\frac{2.7}{6}=\frac{2.475}{5.5}=\frac{1.069}{2.375}=0.45$$

The proportions are all equal. Therefore, we have proven the property of similarity between triangle $\delta$ and triangle $\epsilon .$

Your Turn 10.21

1.

Are these triangles similar? Find the lengths of sides /**/x/**/ and /**/y/**/ to prove your answer.

Figure 10.75

Example 10.22

Applying Similar Triangles

A person who is 5 feet tall is standing 50 feet away from the base of a tree (Figure 10.76). The tree casts a 57-foot shadow. The person casts a 7-foot shadow. What is the height of the tree?

Figure 10.76

Answer

The bigger triangle includes a tree at side $x$ and the smaller triangle includes the person at the side labeled 5 ft. These two triangles are similar because the smaller triangle fits inside the larger triangle at the smallest angle. It would fit inside the larger triangle at either of the other two angles as well. That all angles are equal is one of the criteria for similar triangles, so we can solve using proportions:

$$\begin{array}{ccc}\hfill \frac{5}{7}& \hfill =\hfill & \frac{x}{57}\hfill \\ \hfill 5(57)& \hfill =\hfill & 7x\hfill \\ \hfill \frac{285}{7}& \hfill =\hfill & x=40.7\hfill \end{array}$$

The tree is 40.7 feet tall.

Your Turn 10.22

1.

A person who is 6 feet tall is standing 100 feet away from the base of a tree. The tree casts a shadow 107.5-foot shadow. The person’s shadow is 7.5 feet long. How tall is the tree?

Figure 10.77

Example 10.23

Finding Missing Lengths

At a certain time of day, a radio tower casts a shadow 180 feet long (Figure 10.78). At the same time, a 9-foot truck casts a shadow 15 feet long. What is the height of the tower?

Figure 10.78

Answer

These are similar triangles and the problem can be solved by using proportions:

$$\begin{array}{ccc}\hfill \frac{x}{180}& \hfill =\hfill & \frac{9}{15}\hfill \\ \hfill 9(180)& \hfill =\hfill & 15x\hfill \\ \hfill 1620& \hfill =\hfill & 15x\hfill \\ \hfill 108& \hfill =\hfill & x\hfill \end{array}$$

The height of the tower is 108 ft.

Your Turn 10.23

1.

A tree casts a shadow of 180 feet early in the morning. A 10-foot high garage casts a shadow of 30 feet at the same time in the morning. What is the height of the tree?

People in Mathematics

Thales of Miletus

Thales of Miletus, sixth century BC, is considered one of the greatest mathematicians and philosophers of all time. Thales is credited with being the first to discover that the two angles at the base of an isosceles triangle are equal, and that the two angles formed by intersecting lines are equal—that is, vertical or opposite angles, are equal. Thales is also known for devising a method for measuring the height of the pyramids by similar right triangles. Figure 10.79 shows his method. He measured the length of the shadow cast by the pyramid at the precise time when his own shadow ended at the same place.

Figure 10.79 Thales and Similarity

He equated the vertical height of the pyramid with his own height; the horizontal distance from the pyramid to the tip of its shadow with the distance from himself and the tip of his own shadow; and finally, the length of the shadow cast off the top of the pyramid with length of his own shadow cast off the top of his head. Using proportions, as shown in Figure 10.79, he essentially discovered the properties of similarity for right triangles. That is, $△ABC$ is similar to $△A^{\prime }{B}^{\prime }{C}^{\prime }.$ Note that to be similar, all corresponding angles between the two triangles must be equal, and the proportions from one side to another side within each triangle, as well as the proportions of the corresponding sides between the two triangles must be equal.

Thales is also credited with discovering a method of determining the distance of a ship from the shoreline. Here is how he did it, as illustrated in Figure 10.80.

Figure 10.80 Thales and Similar Triangles

Thales walked along the shoreline pointing a stick at the ship until it formed a ${90}^{\circ }$ angle to the shore. Then he walked along the shot and placed the stick in the ground at point $C$. He continued walking until he reached point $D$. Then, he turned and walked away from the shore at a ${90}^{\circ }$ angle until the stick he placed in the ground at point $C$ lined up with the ship, point $E$. This is how he created similar triangles and estimated the distance of the ship to the shore by using proportions.

Check Your Understanding

17.

Find the measure of the missing angle in the given figure.

18.

Find the measure of the missing angle in the given figure.

19.

In the isosceles triangle shown, find the missing angles.

20.

In the figure shown given /**/\overline {BE}/**/ is parallel to /**/\overline {CD}/**/, find /**/x/**/ and /**/y/**/.

21.

Find /**/a/**/ and /**/t/**/ in the given figure.

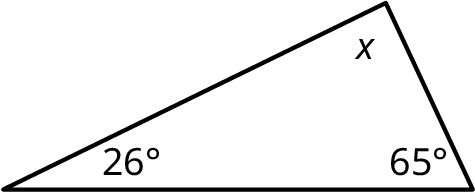
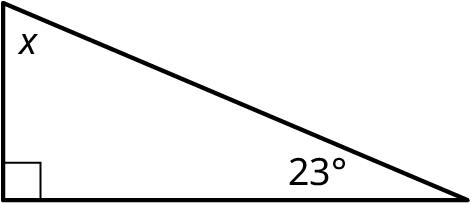
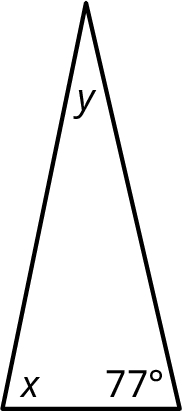
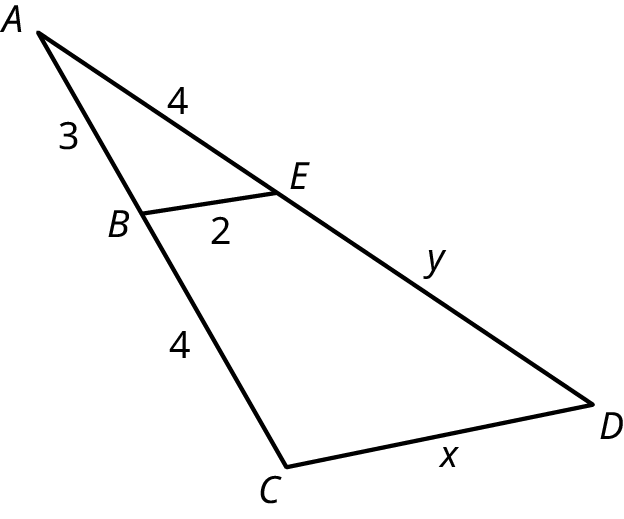
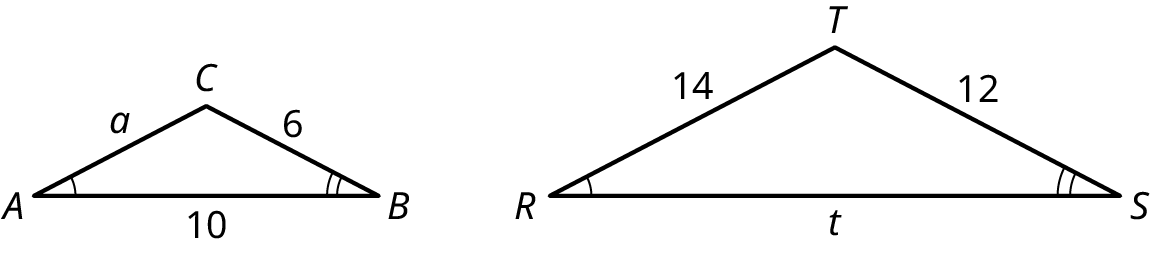
Section 10.3 Exercises

For the following exercises, classify the triangle with the listed angle measurements as acute, right, or obtuse.

1.

/**/m\measuredangle A = {88^ \circ }/**/, /**/m\measuredangle B = {32^ \circ }/**/, /**/m\measuredangle C = {60^ \circ }/**/

2.

/**/m\measuredangle A = {65^ \circ }/**/, /**/m\measuredangle B = {90^ \circ }/**/, /**/m\measuredangle C = {25^ \circ }/**/

3.

/**/m\measuredangle A = {30^ \circ }/**/, /**/m\measuredangle B = {120^ \circ }/**/, /**/m\measuredangle C = {30^ \circ }/**/

4.

/**/m\measuredangle A = {85^ \circ }/**/, /**/m\measuredangle B = {50^ \circ }/**/, /**/m\measuredangle C = {45^ \circ }/**/

5.

Find the missing angles in the given figure.

6.

What are the measurements of each angle in the given figure?

7.

Find the angle measurements in the given figure.

8.

Find the angle measurements in the given figure.

For the following exercises, determine which congruence theorem is used to show that the two triangles are congruent.

9.

10.

11.

12.

Are these triangles similar? If so, what is the common proportion or the scaling factor?

13.

Are the images in the given figure similar? If so, what is the common proportion or the scaling factor?

14.

In the figure shown, given /**/\overline {BE}/**/ is parallel to /**/\overline {CD} ,/**/ find /**/x/**/ and /**/y/**/.

15.

Find /**/a/**/ and /**/t/**/ in the given figure.

16.

In the given figure, find the proportions and solve for /**/a/**/ and /**/b/**/.

17.

In the given figure, find the proportions and solve for /**/r/**/.

18.

A triangular plot of land has a perimeter of 2,400 ft. The longest side is 200 ft less than twice the shortest side. The middle side is 200 ft less than the longest side. Find the lengths of the three sides.

19.

The Orange Tree Hotel in Charleston, North Carolina has a fountain in the shape of a cylinder with a circular foundation. The circumference of the foundation is 6 times the radius increased by 12.88 ft. Find the radius of the circular foundation. (Use 3.14 as an approximation for /**/\pi/**/.)