19.1.2: Right Triangle Trigonometry

Learning Objectives

• Use the Pythagorean Theorem to find the missing lengths of the sides of a right triangle.
• Find the missing lengths and angles of a right triangle.
• Find the exact trigonometric function values for angles that measure \(30^{\circ}\), \(45^{\circ}\), and \(60^{\circ}\).
• Solve applied problems using right-triangle trigonometry.

Introduction

Suppose you have to build a ramp and don’t know how long it needs to be. You know certain angle measurements and side lengths, but you need to find the missing pieces of information.

There are six trigonometric functions, or ratios, that you can use to compute what you don’t know. You will now learn how to use these six functions to solve right-triangle application problems.

Using the Pythagorean Theorem in Trigonometry Problems

There are several ways to determine the missing information in a right triangle. One of these ways is the Pythagorean Theorem, which states that \(a^2 + b^2 = c^2\).

Suppose you have a right triangle in which a and b are the lengths of the legs, and c is the length of the hypotenuse, as shown below.

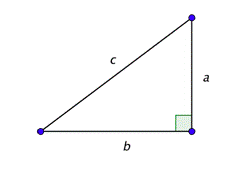
If you know the length of any two sides, then you can use the Pythagorean Theorem (\(a^2 + b^2 = c^2\)) to find the length of the third side. Once you know all the side lengths, you can compute all of the trigonometric functions.

Example

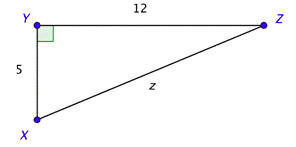
Problem: Find the values of \(tan X\) and \(\sec X\).

Answer

You can immediately find the tangent from the definition and the information in the diagram.

\(\tan X=\frac{\text { opposite }}{\text { adjacent }}=\frac{12}{5}\)

To find the value of the secant, you will need the length of the hypotenuse. Use the Pythagorean Theorem to find the length of the hypotenuse.

\(\begin{array}{c}
5^{2}+12^{2}=z^{2} \\
25+144=z^{2} \\
169=z^{2} \\
13=z
\end{array}\)

Now calculate \(\sec X\) using the definition of secant.

\(\sec X=\frac{\text { hypotenuse }}{\text { adjacent }}=\frac{z}{5}=\frac{13}{5}\)

\(\tan X=\frac{12}{5}, \sec X=\frac{13}{5}\)

Exercise

What is the value of \(\csc R\)?

1. \(\frac{\sqrt{3}}{3}\)
2. \(\frac{3}{\sqrt{3}}\)
3. \(\frac{3}{\sqrt{6}}\)
4. \(\frac{3}{\sqrt{12}}\)

Answer

1. \(\frac{\sqrt{3}}{3}\). Incorrect. You found \(\cos R\) instead of \(\csc R\). Use the Pythagorean Theorem to find the opposite side length. Then divide the hypotenuse by the opposite length. The correct answer is \(\frac{3}{\sqrt{6}}\).
2. \(\frac{3}{\sqrt{3}}\). Incorrect. It looks like you used the wrong angle and found \(\csc T\). Remember that the two acute angles will give you different trigonometric function values. Use the Pythagorean Theorem to find the opposite side length. Divide the hypotenuse by the opposite length. The correct answer is \(\frac{3}{\sqrt{6}}\).
3. \(\frac{3}{\sqrt{6}}\). Correct. You need to know the opposite side length, so use the Pythagorean Theorem: \((\sqrt{3})^{2}+r^{2}=3^{2}\). This simplifies to \(3 + r^2 = 9\). Solving this equation gives you \(r = \sqrt{6}\). Using the definition of cosecant, \(\csc R=\frac{\text { hypotenuse }}{\text { opposite }}=\frac{3}{r}=\frac{3}{\sqrt{6}}\).
4. \(\frac{3}{\sqrt{12}}\). Incorrect. You probably used the correct definition, \(\csc R=\frac{\text { hypotenuse }}{\text { opposite }}\), and used the Pythagorean Theorem to find the opposite side length, \(r\), but set up the equation incorrectly. It should be \((\sqrt{3})^{2}+r^{2}=3^{2}\). The correct answer is \(\frac{3}{\sqrt{6}}\).

Some problems may provide you with the values of two trigonometric ratios for one angle and ask you to find the value of other ratios. However, you really only need to know the value of one trigonometric ratio to find the value of any other trigonometric ratio for the same angle.

Example

Problem: For acute angle \(A\), \(\tan A = \frac{2}{5}\). Find the values of \(\cos A\) and \(\sec A\).

Answer

First you need to draw a right triangle in which \(\tan A = \frac{2}{5}\).

The tangent is the ratio of the opposite side to the adjacent side. The simplest triangle you can use that has that ratio is shown. It has an opposite side of length 2 and an adjacent side of length 5. You could have used a triangle that has an opposite side of length 4 and an adjacent side of length 10. (You just need the ratio to reduce to \(\frac{2}{5}\)).

You can use the Pythagorean Theorem to find the hypotenuse.

\(\begin{array}{c}
5^{2}+2^{2}=h^{2} \\
25+4=h^{2} \\
29=h^{2} \\
\sqrt{29}=h
\end{array}\)

Then use the definition of cosine to find \(\cos A\).

\(\cos A=\frac{\text { adjacent }}{\text { hypotenuse }}=\frac{5}{\sqrt{29}}\)

Now use the fact that \(\sec A=\frac{1}{\cos A}\) to find \(\sec A\).

\(\sec A=\frac{1}{\cos A}=\frac{1}{\frac{5}{\sqrt{29}}}=\frac{\sqrt{29}}{5}\)

\(\cos A=\frac{5}{\sqrt{29}}, \sec A=\frac{\sqrt{29}}{5}\)

Example

Problem: If angle \(X\) is an acute angle with \(\sin X = \frac{3}{4}\), what is the value of \(\cot X\)?

Answer

In this right triangle, because \(\sin X = \frac{3}{4}\), the ratio of the opposite side to the hypotenuse is \(\frac{3}{4}\). The simplest triangle we can use that has that ratio would be the triangle that has an opposite side of length 3 and a hypotenuse of length 4.

We can use the Pythagorean Theorem to find the unknown leg length.

\(\begin{array}{c}
y^{2}+3^{2}=4^{2} \\
y^{2}+9=16 \\
y^{2}=7 \\
y=\sqrt{7}
\end{array}\)

You can find the cotangent using the definition.

\(\cot X=\frac{\text { adjacent }}{\text { opposite }}=\frac{y}{3}=\frac{\sqrt{7}}{3}\)

Or you can find the cotangent by first finding tangent and then taking the reciprocal.

\(\begin{array}{l}
\tan X=\frac{\text { opposite }}{\text { adjacent }}=\frac{3}{y}=\frac{3}{\sqrt{7}} \\
\cot X=\frac{1}{\tan X}=\frac{1}{\frac{3}{\sqrt{7}}}=\frac{\sqrt{7}}{3}
\end{array}\)

\(\cot X=\frac{\sqrt{7}}{3}\)

Solving Right Triangles

Determining all of the side lengths and angle measures of a right triangle is known as solving a right triangle. Let’s look at how to do this when you’re given one side length and one acute angle measure. Once you learn how to solve a right triangle, you’ll be able to solve many real world applications, such as the ramp problem at the beginning of this lesson, and the only tools you’ll need are the definitions of the trigonometric functions, the Pythagorean Theorem, and a calculator.

Example

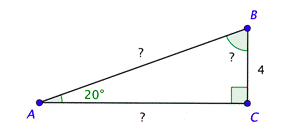
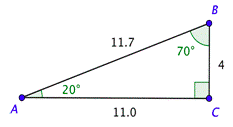
Problem: You need to build a ramp with the following dimensions. Solve the right triangle shown below. Use the approximations \(\csc 20^{\circ} \approx 2.92\) and \(\tan 20^{\circ} \approx 0.364\), and give the lengths to the nearest tenth.

Answer

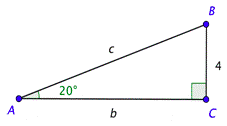
Remember that the acute angles in a right triangle are complementary, which means their sum is \(90^{\circ}\). Since \(m \angle A=20^{\circ}\), it follows that \(m \angle B=90^{\circ}-20^{\circ}=70^{\circ}\).

You can use the definition of cosecant to find \(c\). Substitute the measure of the angle on the left side of the equation and use the triangle to set up the ratio on the right. Solving the equation and rounding to the nearest tenth gives you \(c \approx 11.7\).

\(\begin{array}{c}
\csc 20^{\circ}=\frac{\text { hypotenuse }}{\text { opposite }} \\
2.92 \approx \frac{c}{4} \\
4(2.92) \approx c \\
11.68 \approx c
\end{array}\)

In a similar way, you can use the definition of tangent and the measure of the angle to find \(b\). Solving the equation and rounding to the nearest tenth gives you \(b \approx 11.0\).

\(\begin{array}{c}
\tan 20^{\circ}=\frac{\text { opposite }}{\text { adjacent }} \\
0.364 \approx \frac{4}{b} \\
0.364 b \approx 4 \\
b \approx \frac{4}{0.364} \approx 10.989
\end{array}\)

The ramp needs to be 11.7 feet long.

In the problem above, you were given the values of the trigonometric functions. In the next problem, you’ll need to use the trigonometric function keys on your calculator to find those values.

Example

Problem: Solve the right triangle shown below. Give the lengths to the nearest tenth.

Answer

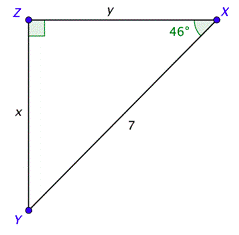
The acute angles are complementary, which means their sum is \(90^{\circ}\). Since \(\text { Since } m \angle X=46^{\circ}\), it follows that \(m \angle Y=90^{\circ}-46^{\circ}=44^{\circ}\).

You can use the definition of sine to find \(x\). Use your calculator to find the value of \(\sin 46^{\circ}\) and the triangle to set up the ratio on the right. Solving the equation and rounding to the nearest tenth gives you \(x \approx 5.0\).

\(\begin{array}{c}
\sin 46^{\circ}=\frac{\text { opposite }}{\text { hypotenuse }} \\
0.72 \approx \frac{x}{7} \\
7(0.72) \approx x \\
5.04 \approx x
\end{array}\)

To find \(y\), you can either use another trigonometric function (such as cosine) or you can use the Pythagorean Theorem. Solving the equation and rounding to the nearest tenth gives you \(y \approx 4.9\).

\(\begin{array}{c}
5.0^{2}+y^{2} \approx 7^{2} \\
25+y^{2} \approx 49 \\
y^{2} \approx 24 \\
y \approx \sqrt{24} \\
y \approx 4.899
\end{array}\)

We now know all three sides and all three angles. Their values are shown in the drawing.

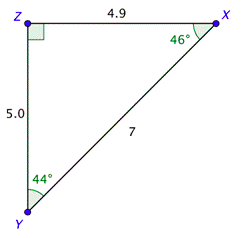
Sometimes you may be given enough information about a right triangle to solve the triangle, but that information may not include the measures of the acute angles. In this situation, you will need to use the inverse trigonometric function keys on your calculator to solve the triangle.

Example

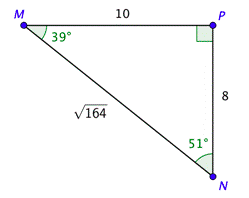
Problem: Solve the right triangle shown below, given that \(\cot N =\frac{4}{5}\). Find the exact side lengths and approximate the angles to the nearest degree.

Answer

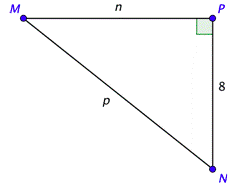
You are not given an angle measure, but you can use the definition of cotangent to find the value of \(n\).

Use the ratio you are given on the left side and the information from the triangle on the right side. Cross-multiply and solve for \(n\).

\(\begin{aligned}
\cot N &=\frac{\text { adjacent }}{\text { opposite }} \\
\frac{4}{5} &=\frac{8}{n} \\
4 n &=40 \\
n &=10
\end{aligned}\)

Use the Pythagorean Theorem to find the value of \(p\).

\(\begin{array}{c}
10^{2}+8^{2}=p^{2} \\
100+64=p^{2} \\
164=p^{2} \\
\sqrt{164}=p
\end{array}\)

We can use the triangle to find a value of the tangent and the inverse tangent key on your calculator to find the angle that yields that value. Rounding to the nearest degree, \(\angle M\) is approximately \(39^{\circ}\), \(M \approx 39^{\circ}\). Subtract \(39^{\circ}\), from \(90^{\circ}\) to get \(N \approx 51^{\circ}\).

\(\begin{array}{c}
\tan M=\frac{8}{10}=0.8 \\
M=\tan ^{-1} 0.8 \\
M \approx 38.7^{\circ}
\end{array}\)

We now know all three sides and all three angles. Their values are shown in the drawing.

Exercise

What is the value of \(x\) to the nearest hundredth?

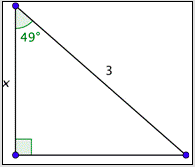
1. 4.57
2. 1.97
3. 0.90
4. 0.22

Answer

1. 4.57. Incorrect. You probably set up the ratio incorrectly, equating \(\cos 49^{\circ}\) and \(\frac{3}{x}\). A correct way to set up the equation is \(\cos 49^{\circ}=\frac{x}{3}\). The correct answer is 1.97.
2. 1.97. Correct. One way to set up a correct equation is to use the definition of cosine. This will give you \(\cos 49^{\circ}=\frac{x}{3}\). The solution to this equation is: \(x=3 \cdot \cos 49^{\circ} \approx 3 \cdot(0.656)=1.968\). This rounds to 1.97.
3. 0.90. Incorrect. You probably set up the correct equation, \(\cos 49^{\circ}=\frac{x}{3}\), and solved it correctly. However, your calculator was not set to degrees. The correct answer is 1.97.
4. 0.22. Incorrect. You may have correctly set up your equation as \(\cos 49^{\circ}=\frac{x}{3}\), but then incorrectly solved it as \(x=\frac{\cos 49^{\circ}}{3}\). The correct answer is 1.97.

Special Angles

As a general rule, you need to use a calculator to find the values of the trigonometric functions for any particular angle measure. However, angles that measure \(30^{\circ}\), \(45^{\circ}\), and \(60^{\circ}\), which you will see in many problems and applications, are special. You can find the exact values of these functions without a calculator. Let’s see how.

Suppose you had a right triangle with an acute angle that measured \(45^{\circ}\). Since the acute angles are complementary, the other one must also measure \(45^{\circ}\). Because the two acute angles are equal, the legs must have the same length, for example, 1 unit.

You can determine the hypotenuse using the Pythagorean Theorem.

\(\begin{array}{c}
1^{2}+1^{2}=h^{2} \\
1+1=h^{2} \\
2=h^{2} \\
\sqrt{2}=h
\end{array}\)

Now you have all the sides and angles in this right triangle.

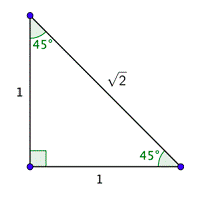
You can use this triangle (which is sometimes called a \(45^{\circ}\) - \(45^{\circ}\) - \(90^{\circ}\) triangle) to find all of the trigonometric functions for \(45^{\circ}\). One way to remember this triangle is to note that the hypotenuse is \(\sqrt{2}\) times the length of either leg.

Example

Problem: Find the values of the six trigonometric functions for \(45^{\circ}\) and rationalize denominators, if necessary.

Answer

Use the definitions of sine, cosine and tangent. Notice that because the opposite and adjacent sides are equal, sine and cosine are equal.

\(\begin{array}{c}
\sin 45^{\circ}=\frac{\text { opposite }}{\text { hypotenuse }}=\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2} \\
\cos 45^{\circ}=\frac{\text { adjacent }}{\text { hypotenuse }}=\frac{1}{\sqrt{2}}=\frac{1}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2} \\
\tan 45^{\circ}=\frac{1}{1}=1
\end{array}\)

Use the reciprocal identities. Notice that because the opposite and adjacent sides are equal, cosecant and secant are equal.

\(\begin{array}{r}
\csc 45^{\circ}=\frac{1}{\sin 45^{\circ}}=\frac{1}{\frac{1}{\sqrt{2}}}=\frac{\sqrt{2}}{1}=\sqrt{2} \\
\sec 45^{\circ}=\frac{1}{\cos 45^{\circ}}=\frac{1}{\frac{1}{\sqrt{2}}}=\frac{\sqrt{2}}{1}=\sqrt{2} \\
\cot 45^{\circ}=\frac{1}{\tan 45^{\circ}}=\frac{1}{1}=1
\end{array}\)

\(\begin{array}{l}
\sin 45^{\circ}=\cos 45^{\circ}=\frac{\sqrt{2}}{2}, \tan 45^{\circ}=1 \\
\csc 45^{\circ}=\sec 45^{\circ}=\sqrt{2}, \cot 45^{\circ}=1
\end{array}\)

You can construct another triangle that you can use to find all of the trigonometric functions for \(30^{\circ}\) and \(60^{\circ}\). Start with an equilateral triangle with side lengths equal to 2 units. If you split the equilateral triangle down the middle, you produce two triangles with \(30^{\circ}\), \(60^{\circ}\) and \(90^{\circ}\) angles. These two right triangles are congruent. They both have a hypotenuse of length 2 and a base of length 1.

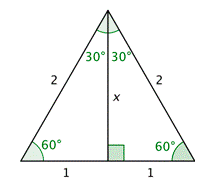
You can determine the height using the Pythagorean Theorem.

\(\begin{array}{c}
x^{2}+1^{2}=2^{2} \\
x^{2}+1=4 \\
x^{2}=3 \\
x=\sqrt{3}
\end{array}\)

Here is the left half of the equilateral triangle turned on its side.

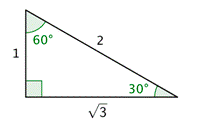
You can use this triangle (which is sometimes called a \(30^{\circ}\) - \(60^{\circ}\) - \(90^{\circ}\) triangle) to find all of the trigonometric functions for \(30^{\circ}\) and \(60^{\circ}\). Note that the hypotenuse is twice as long as the shortest leg, which is opposite the \(30^{\circ}\) angle, so that \(\sin 30^{\circ}=\frac{1}{2}\). The length of the longest leg, which is opposite the \(60^{\circ}\) angle is \(\sqrt{3}\) times the length of the shorter leg.

Example

Problem: Find the values of \(\cos 30^{\circ}\), \(\tan 60^{\circ}\), \(\sec 30^{\circ}\), and \(\cot 60^{\circ}\). Rationalize denominators, if necessary.

Answer

Use the definitions of sine, cosine and tangent. For each angle, be sure to use the legs that are opposite and adjacent to that angle. For example, \(\sqrt{3}\) is opposite to \(60^{\circ}\), but adjacent to \(30^{\circ}\).

\(\begin{array}{r}
\cos 30^{\circ}=\frac{\sqrt{3}}{2} \\
\tan 60^{\circ}=\frac{\sqrt{3}}{1}=\sqrt{3}
\end{array}\)

Remember that secant is the reciprocal of cosine and that cotangent is the reciprocal of tangent. Rationalize the denominators.

\(\begin{array}{r}
\sec 30^{\circ}=\frac{1}{\frac{\sqrt{3}}{2}}=\frac{2}{\sqrt{3}}=\frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{2 \sqrt{3}}{3} \\
\cot 60^{\circ}=\frac{1}{\sqrt{3}}=\frac{1}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{\sqrt{3}}{3}
\end{array}\)

\(\begin{array}{l}
\cos 30^{\circ}=\frac{\sqrt{3}}{2}, \sec 30^{\circ}=\frac{2 \sqrt{3}}{3} \\
\tan 60^{\circ}=\sqrt{3}, \cot 60^{\circ}=\frac{\sqrt{3}}{3}
\end{array}\)

You can use the information from the \(30^{\circ}\) - \(60^{\circ}\) - \(90^{\circ}\) and \(45^{\circ}\) - \(45^{\circ}\) - \(90^{\circ}\) triangles to solve similar triangles without using a calculator.

Example

Problem: What is the value of \(x\) in the triangle below?

Answer

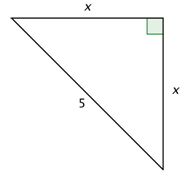
Since the two legs have the same length, the two acute angles must be equal, so they are each \(45^{\circ}\).

In a \(45^{\circ}\) - \(45^{\circ}\) - \(90^{\circ}\) triangle, the length of the hypotenuse is times the length of a leg. You can use this relationship to find \(x\). Remember to rationalize the denominator.

\(\begin{aligned}
\sqrt{2} \cdot x &=5 \\
x &=\frac{5}{\sqrt{2}} \\
&=\frac{5}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} \\
&=\frac{5 \sqrt{2}}{2}
\end{aligned}\)

Here is another way you can solve this problem. You can use the definition of sine to find \(x\).

\(\begin{aligned}
\sin 45^{\circ} &=\frac{x}{5} \\
5 \cdot \sin 45^{\circ} &=x \\
5 \cdot \frac{1}{\sqrt{2}} &=x \\
\frac{5}{\sqrt{2}} &=x \\
x &=\frac{5 \sqrt{2}}{2}
\end{aligned}\)

\(x=\frac{5 \sqrt{2}}{2}\)

You also could have solved the last problem using the Pythagorean Theorem, which would have produced the equation \(x^2 + x^2 = 5^2\).

Example

Problem: Solve the right triangle shown below.

Answer

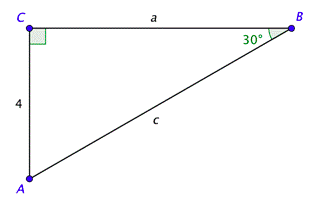
The acute angles are complementary, so \(m \angle A=60^{\circ}\). This is a \(30^{\circ}\) - \(60^{\circ}\) - \(90^{\circ}\) triangle. We can now use the trigonometric functions to find the lengths of the missing sides.

Since we know all the measures of the angles, we now need to find the lengths of the missing sides. To find \(c\) (the length of the hypotenuse), we can use the sine function because we know that \(\sin 30^{\circ}=\frac{1}{2}\) and we know the length of the opposite side.

\(\begin{array}{c}
\sin 30^{\circ}=\frac{4}{c} \\
\frac{1}{2}=\frac{4}{c} \\
c=8
\end{array}\)

To find \(a\) (the length of the side opposite angle \(A\)), we can use the tangent function because we know that \(\tan 60^{\circ}=\sqrt{3}\) and we know the length of the adjacent side.

\(\begin{array}{c}
\tan 60^{\circ}=\frac{a}{4} \\
\sqrt{3}=\frac{a}{4} \\
4 \sqrt{3}=a
\end{array}\)

We now know all three sides and all three angles. Their values are shown in the drawing.

Exercise

If \(\cos x = \frac{1}{2}\), what is the value of \(\csc x\)?

1. 2
2. \(\frac{\sqrt{3}}{3}\)
3. \(\frac{\sqrt{6}}{3}\)
4. \(\frac{2 \sqrt{3}}{3}\)

Answer

1. 2. Incorrect. Refer to the \(30^{\circ}\) - \(60^{\circ}\) - \(90^{\circ}\) triangle. From there you can see that \(\cos 60^{\circ}=\frac{1}{2}\). It follows that \(x = 60^{\circ}\). You may have used the wrong angle and found \(\csc 30^{\circ}\) or used the correct angle but found \(\sec 60^{\circ}\). You need to find \(\csc 60^{\circ}\). The correct answer is \(\frac{2 \sqrt{3}}{3}\).
2. \(\frac{\Incorrect. Refer to the \(30^{\circ}\) - \(60^{\circ}\) - \(90^{\circ}\) triangle. From there you can see that \(\cos 60^{\circ}=\frac{1}{2}\). It follows that \(x=60^{\circ}\). You may have mistakenly found \(\cot 60^{\circ}\). You need to find \(\csc 60^{\circ}\). The correct answer is \(\frac{2 \sqrt{3}}{3}\).
3. \(\frac{\sqrt{6}}{3}\). Incorrect. You may have correctly found \(\csc 60^{\circ}\), but made a mistake when rationalizing the denominator. The correct answer is \(\frac{2 \sqrt{3}}{3}\).
4. \(\frac{2 \sqrt{3}}{3}\). Correct. Refer to the \(30^{\circ}\) - \(60^{\circ}\) - \(90^{\circ}\) triangle. From there you can see that \(\cos 60^{\circ}=\frac{1}{2}\). It follows that \(x=60^{\circ}\). So \(\csc x=\csc 60^{\circ}=\frac{2}{\sqrt{3}}=\frac{2}{\sqrt{3}} \cdot \frac{\sqrt{3}}{\sqrt{3}}=\frac{2 \sqrt{3}}{3}\).

Using Trigonometry in Real-World Problems

There are situations in the real world, such as building a ramp for a loading dock, in which you have a right triangle with certain information about the sides and angles, and you wish to find unknown measures of sides or angles. This is where understanding trigonometry can help you.

Example

Problem: Ben and Emma are out flying a kite. Emma can see that the kite string she is holding is making a \(70^{\circ}\) angle with the ground. The kite is directly above Ben, who is standing 50 feet away. To the nearest foot, how many feet of string has Emma let out?

Answer

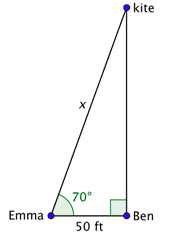
We want to find the length of string let out. It is the hypotenuse of the right triangle shown.

Since the 50-foot distance measures the adjacent side to the \(70^{\circ}\) angle, you can use the cosine function to find \(x\).

\(\cos 70^{\circ}=\frac{50}{x}\)

Solve the equation for \(x\). Use a calculator to find a numerical value. The answer rounds to 146.

\(\begin{array}{c}
x \cdot \cos 70^{\circ}=50 \\
x=\frac{50}{\cos 70^{\circ}} \\
x=\frac{50}{0.342 \ldots} \\
x=146.19 \ldots
\end{array}\)

Emma has let out approximately 146 feet of string.

In the example above, you were given one side and an acute angle. In the next one, you’re given two sides and asked to find an angle. Finding an angle will usually involve using an inverse trigonometric function. The Greek letter theta, \(\theta\), is commonly used to represent an unknown angle. In this example, \(\theta\) represents the angle of elevation.

Example

Problem: A wheelchair ramp is placed over a set of stairs so that one end is 2 feet off the ground. The other end is at a point that is a horizontal distance of 28 feet away, as shown in the diagram. What is the angle of elevation to the nearest tenth of a degree?

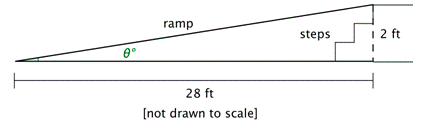
Answer

The angle of elevation is labeled \(\theta ^{\circ}\) in the diagram. The lengths given are the sides opposite and adjacent to this angle, so you can use the tangent function to find \(\theta\).

You want to find the measure of an angle that gives you a certain tangent value. This means that you need to find the inverse tangent. Remember that you have to use the keys 2ND and TAN on your calculator. Look at the hundredths place to round to the nearest tenth.

\(\begin{aligned}
\tan \theta^{\circ} &=\frac{2}{28} \\
\tan \theta^{\circ} &=\frac{1}{14} \\
\theta^{\circ} &=\tan ^{-1}\left(\frac{1}{14}\right) \\
\theta &=4.0856 \ldots
\end{aligned}\)

The angle of elevation is approximately \(4.1^{\circ}\).

Remember that problems involving triangles with certain special angles can be solved without the use of a calculator.

Example

Problem: A fence is used to make a triangular enclosure with the longest side equal to 30 feet, as shown below. What is the exact length of the side opposite the \(60^{\circ}\) angle?

Answer

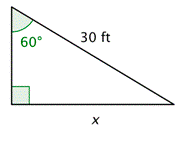
Call the unknown length \(x\). Since you know the length of the hypotenuse, you can use the sine function.

This is a \(30^{\circ}\) - \(60^{\circ}\) - \(90^{\circ}\) triangle. Therefore, you can find the exact value of the trigonometric function without using a calculator.

\(\begin{array}{l}
\sin 60^{\circ}=\frac{x}{30} \\
\frac{\sqrt{3}}{2}=\frac{x}{30}
\end{array}\)

Solve the equation for \(x\).

\(x=\frac{30 \sqrt{3}}{2}=15 \sqrt{3}\)

The exact length of the side opposite the \(60^{\circ}\) angle is 15\(\sqrt{3}\) feet.

Sometimes the right triangle can be part of a bigger picture.

Exercise

A guy wire is attached to a telephone pole 3 feet below the top of the pole, as shown below. The guy wire is anchored 14 feet from the telephone pole and makes a \(64^{\circ}\) angle with the ground. How high up the pole is the guy wire attached? Round your answer to the nearest tenth of a foot.

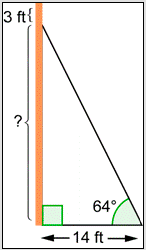
1. \(14 \cdot \sin 64^{\circ} \approx 12.6 \text { feet }\)
2. \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\)
3. \(14 \cdot \tan 64^{\circ}+3 \approx 31.7 \text { feet }\)
4. \(\frac{14}{\cos 64^{\circ}} \approx 31.9 \text { feet }\)

Answer

1. \(14 \cdot \sin 64^{\circ} \approx 12.6 \text { feet }\). Incorrect. You may have been confused as to which ratio corresponds to which trigonometric function. You need to solve the equation \(\tan 64^{\circ}=\frac{x}{14}\), where \(x\) represents the vertical distance from the base of the telephone pole up to where the guy wire is attached. The correct answer is \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
2. \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\). Correct. Let \(x\) represent the vertical distance from the base of the telephone pole up to where the guy wire is attached. Then \(\tan 64^{\circ}=\frac{x}{14}\). Solving this equation for \(x\) gives you \(x=14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
3. \(14 \cdot \tan 64^{\circ}+3 \approx 31.7 \text { feet }\). Incorrect. It looks like you set up and solved the correct equation to find the unknown length. However, you misread the problem. When you added the 3 you found the height of the entire pole. The correct answer is \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).
4. \(\frac{14}{\cos 64^{\circ}} \approx 31.9 \text { feet }\). Incorrect. It looks like you set up and solved an equation to find the length of the wire (the hypotenuse of the triangle). You need to solve the equation \(\tan 64^{\circ}=\frac{x}{14}\), where \(x\) represents the vertical distance from the base of the telephone pole up to where the guy wire is attached. The correct answer is \(14 \cdot \tan 64^{\circ} \approx 28.7 \text { feet }\).

Summary

There are many ways to find the missing side lengths or angle measures in a right triangle. Solving a right triangle can be accomplished by using the definitions of the trigonometric functions and the Pythagorean Theorem. This process is called solving a right triangle. Being able to solve a right triangle is useful in solving a variety of real-world problems such as the construction of a wheelchair ramp.

You can find the exact values of the trigonometric functions for angles that measure \(30^{\circ}\), \(45^{\circ}\), and \(60^{\circ}\). You can find exact values for the sides in \(30^{\circ}\), \(45^{\circ}\), and \(60^{\circ}\) triangles if you remember that \(\sin 45^{\circ}=\frac{1}{\sqrt{2}}\) and \(\sin 30^{\circ}=\frac{1}{2}\). For other angle measures, it is necessary to use a calculator to find approximate values of the trigonometric functions.