2.6: Addition and Subtraction with Other Bases

Last updated
Save as PDF

Page ID: 59936

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Addition in Other Bases

As we saw in the previous section with the Mayan numeration system, we can add or subtract in other bases. Below are a series of steps, but, overall, we add as usual while finding its equivalent number from base 10 to the new base.

Adding in Base b

Rewrite the addition vertically, if not already.
Start in the ones place (as usual), but find the number the sum represents in base b.
If the sum is larger than base b, then carry over to the b¹ place value.
Repeat steps 2 and 3 for the b², b³, … place values.

Example $\PageIndex{1}$

Add in base two: 111_two + 11_two

Solution

Writing this vertically, we get

$ 111_{two} $

$\\ + \underline{11_{two}} $

Let’s add the ones place as usual. If we were in base 10, 1+1=2; 2 in base 10 is equivalent to 0 in base 2 and we carry 1 over to the 2’s place. Recall, base two is {0,1}. Hence, the ones place is 0:

$ 11^{+1}1_{two} $

$\\ + \underline{ 1 \;\;\; 1_{two}} $

$\; 1 \;\; 0_{two} $

Adding in the 2’s place, 1+1+1=3 in base 10, but 3 is 1 in base 2 and we carry 1 to the 2²’s place:

$ 1^{+1}11_{two} $

$ + \underline{\;\;\;11_{two}} $

$ 0 \;\;\; 10_{two} $

Adding in the 2²’s place, we get 1+1=2 in base 10, but 2 in base 10 is 0 in base 2 and we carry a 1 over to the 2³’s place:

$ +1\;1\;11_{two} $

$ + \underline{\;\;\;\;\;11_{two}} $

$ 1 \;\;\; 010_{two} $

Hence, 111_two + 11_two = 1010_two. Note, another way to do this is convert each number to base 10 and add as usual, then convert the result back into base 2.

Example $\PageIndex{2}$

Add in base five: 44_five + 42_five

Solution

Let’s try this by converting each number to base 10, adding them, then converting the sum back into base 5:

44_five = 4(5) + 4(1) = 24_ten

42_five = 4(5) + 2(1) = 22_ten

Next, we add the base 10 numbers:

24 + 22 = 46_ten

Converting 46 in base ten into a number in base 5, we use the previous sections’ technique and obtain 141_five. Thus, 46 in base 10 is equivalent to 141 in base 5.

Subtraction in Other Bases

Subtracting in Base b

Rewrite the subtraction vertically, if not already.

Start in the ones place (as usual), but find the number the difference represents in base b.

If the ones place of the minuend is smaller than the ones place of the subtrahend, then borrow from the place value to the left in that base b. Then subtract as usual.

Repeat steps 2 and 3 for the b², b³ place values.

Example $\PageIndex{3}$

Subtract in base 5: 240_five - 40_five

Solution

$ 240_{five} $

$- \underline{40_{five}} $

If we take the ones place, 0-0 =0, which is 0 in base 5, then the ones place stays 0.

$ 240_{five} $

$- \underline{40_{five}} $

$ 0$

Now let’s take the 5’s place: 4-4=0. Since 0 is in base 5, then the 5’s place is 0.

$ 240_{five} $

$- \underline{40_{five}} $

$ 00\;$

Let’s look at the 5²’s place. Notice, we can just drop the two down and get

$ 240_{five} $

$- \underline{40_{five}} $

$ 200_{5}\;\;$

Thus, 240_five - 40_five = 200_five.

What if we have to borrow? We can subtract with borrowing easily in base 10, but what if we wanted to subtract two numbers that included borrowing? Let’s see.

Example $\PageIndex{4}$

Subtract in base 5: 404_five - 323_five

Solution

Rewriting this vertically, we get

$ 404_{five} $

$- \underline{323_{five}} $

Subtracting in the ones place, we get 4-3=1. Since 1 is in base 5, then the ones place is 1.

$\; 404_{five} $

$- \underline{323_{five}} $

$ 1$

Looking at the 5’s place, notice that 0 is less than 2 and we have to borrow from the 52 ’s place. Recall, we are in base 5, so when we borrow, we still reduce 4 to 3, but we carry 5 since we are in base 5:

$\; 4^3 0^5 4_{five} $

$- \underline{3\;2\;3_{five}} $

$ 0\;3\;1_{five}$

Now, we subtract as usual: 5-2 = 3. Since 3 is in base 5, then the 5’s place is 3. Subtracting in the 5²’s place, we get 3-3=0; hence, the 5²’s place is 0.

Thus, 404_five - 323_five = 31_five.

Conclusion

In this chapter, we have briefly sketched the development of numbers and our counting system, with the emphasis on the “brief” part. There are numerous sources of information and research that fill many volumes of books on this topic. Unfortunately, we cannot begin to come close to covering all of the information that is out there.

We have only scratched the surface of the wealth of research and information that exists on the development of numbers and counting throughout human history. It is important to note that the system that we use every day is a product of thousands of years of progress and development. It represents contributions by many civilizations and cultures. It does not come down to us from the sky, a gift from the gods. It is not the creation of a textbook publisher. It is indeed as human as we are, as is the rest of mathematics. Behind every symbol, formula, and rule there is a human face to be found, or at least sought.

Furthermore, we hope that you now have a basic appreciation for just how interesting and diverse number systems can get. Also, we’re pretty sure that you have also begun to recognize that we take our own number system for granted so much that when we try to adapt to other systems or bases, we find ourselves truly having to concentrate and think about what is going on.

Try It Now Answers

1. 1+6×3+3×6+2×12 = 61 cats.

2. From left to right:

Cord 1 = 2,162

Cord 2 = 301

Cord 3 = 0

Cord 4 = 2,070

3. 41065₇ = 9994₁₀

4. 143₁₀ = 1033₅

5. 21021₃ = 196₁₀

6. 657₁₀ = 22101₄

7. 8377₁₀ = 20271₈

8. 9352₁₀ = 244402₅

9. 1500₁₀ = 2001120₃

10. 1562

11. 10553₁₀ = 1,6,7,13₂₀

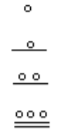
$clipboard_e7548f62e1f32a2979fb187c315bc3ec3.png$

12. 5617₁₀ = 14,0,17₂₀. Note that there is a zero in the 20’s place, so you’ll need to use the appropriate zero symbol in between the ones and 400’s places.

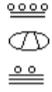
$clipboard_e89e7512138970320ff474a9ab55c0cfe.png$

13. A sample solution is shown.

$clipboard_e04e15dbab44baaee8c71766372f8b564.png$

Search

Adding in Base b

Example \(\PageIndex{1}\)

Solution

Example \(\PageIndex{2}\)

Solution

Subtracting in Base b

Example \(\PageIndex{3}\)

Solution

Example \(\PageIndex{4}\)

Solution

Try It Now Answers