13.4: Cardinality
- Page ID
- 34258
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Often times we are interested in the number of items in a set or subset. This is called the cardinality of the set.
The number of elements in a set is the cardinality of that set.
The cardinality of the set \(A\) is often notated as \(|A|\) or \(n(A)\)
Let \(A=\{1,2,3,4,5,6\}\) and \(B=\{2,4,6,8\}\)
What is the cardinality of \(B ? A \cup B, A \cap B ?\)
Solution
The cardinality of \(B\) is \(4,\) since there are 4 elements in the set.
The cardinality of \(A \cup B\) is \(7,\) since \(A \cup B=\{1,2,3,4,5,6,8\},\) which contains 7 elements.
The cardinality of \(A \cap B\) is 3 , since \(A \cap B=\{2,4,6\}\), which contains 3 elements.
What is the cardinality of \(P=\) the set of English names for the months of the year?
Solution
The cardinality of this set is \(12,\) since there are 12 months in the year.
Sometimes we may be interested in the cardinality of the union or intersection of sets, but not know the actual elements of each set. This is common in surveying.
A survey asks 200 people “What beverage do you drink in the morning”, and offers choices:
- Tea only
- Coffee only
- Both coffee and tea
Suppose 20 report tea only, 80 report coffee only, 40 report both. How many people drink tea in the morning? How many people drink neither tea or coffee?
Solution
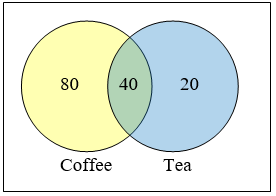This question can most easily be answered by creating a Venn diagram. We can see that we can find the people who drink tea by adding those who drink only tea to those who drink both: 60 people.
We can also see that those who drink neither are those not contained in the any of the three other groupings, so we can count those by subtracting from the cardinality of the universal set, 200.
\(200-20-80-40=60\) people who drink neither.
A survey asks: Which online services have you used in the last month:
- Have used both
The results show 40% of those surveyed have used Twitter, 70% have used Facebook, and 20% have used both. How many people have used neither Twitter or Facebook?
Solution
Let \(T\) be the set of all people who have used Twitter, and \(F\) be the set of all people who have used Facebook. Notice that while the cardinality of \(F\) is \(70 \%\) and the cardinality of \(T\) is \(40 \%\), the cardinality of \(F \cup T\) is not simply \(70 \%+40 \%\), since that would count those who use both services twice. To find the cardinality of \(F \cup T\), we can add the cardinality of \(F\) and the cardinality of \(T\), then subtract those in intersection that we've counted twice. In symbols,
\(\mathrm{n}(F \cup T)=\mathrm{n}(F)+\mathrm{n}(T)-\mathrm{n}(F \cap T)\)
\(\mathrm{n}(F \cup T)=70 \%+40 \%-20 \%=90 \%\)
Now, to find how many people have not used either service, we're looking for the cardinality of \((F \cup T)^{c}\). since the universal set contains \(100 \%\) of people and the cardinality of \(F \cup T=90 \%\), the cardinality of \((F \cup 7)^{c}\) must be the other \(10 \%\)
The previous example illustrated two important properties
\(\mathrm{n}(A \cup B)=\mathrm{n}(A)+\mathrm{n}(B)-\mathrm{n}(A \cap B)\)
\(n\left(A^{\circ}\right)=n(U)-n(A)\)
Notice that the first property can also be written in an equivalent form by solving for the cardinality of the intersection:
\(\mathrm{n}(A \cap B)=\mathrm{n}(A)+\mathrm{n}(B)-\mathrm{n}(A \cup B)\)
Add text here.Fifty students were surveyed, and asked if they were taking a social science (SS), humanities (HM) or a natural science (NS) course the next quarter.
\(\begin{array}{ll} \text{21 were taking a SS course} & \text{26 were taking a HM course} \\ \text{19 were taking a NS course} & \text{9 were taking SS and HM} \\ \text{7 were taking SS and NS} & \text{10 were taking HM and NS} \\ \text{3 were taking all three} & \text{7 were taking none} \end{array}\)
How many students are only taking a SS course?
Solution
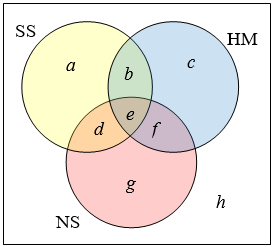It might help to look at a Venn diagram.
From the given data, we know that there are 3 students in region \(e\) and 7 students in region \(h\)
since 7 students were taking a \(S S\) and \(N S\) course, we know that \(n(d)+n(e)=7\). since we know there are 3 students in region 3 , there must be
\(7-3=4\) students in region \(d\)
Similarly, since there are 10 students taking \(\mathrm{HM}\) and \(\mathrm{NS}\), which includes regions \(e\) and \(f\), there must be
\(10-3=7\) students in region \(f\)
Since 9 students were taking \(\mathrm{SS}\) and \(\mathrm{HM}\), there must be \(9-3=6\) students in region \(b\)
Now, we know that 21 students were taking a SS course. This includes students from regions \(a, b, d,\) and \(e .\) since we know the number of students in all but region \(a,\) we can determine that \(21-6-4-3=8\) students are in region \(a\)
8 students are taking only a SS course.
One hundred fifty people were surveyed and asked if they believed in UFOs, ghosts, and Bigfoot.
\(\begin{array}{ll} \text{43 believed in UFOs} & \text{44 believed in ghosts} \\ \text{25 believed in Bigfoot} & \text{10 believed in UFOs and ghosts} \\ \text{8 believed in ghosts and Bigfoot} & \text{5 believed in UFOs and Bigfoot} \\ \text{2 believed in all three} & \text{} \end{array}\)
How many people surveyed believed in at least one of these things?
- Answer
-
Starting with the intersection of all three circles, we work our way out. since 10 people believe in UFOs and Ghosts, and 2 believe in all three, that leaves 8 that believe in only UFOs and Ghosts. We work our way out, filling in all the regions. Once we have, we can add up all those regions, getting 91 people in the union of all three sets. This leaves \(150-91=59\) who believe in none.