13.5: Exercises

Last updated
Save as PDF

Page ID: 34259

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

1. List out the elements of the set “The letters of the word Mississipi”

2. List out the elements of the set “Months of the year”

3. Write a verbal description of the set $\{3,6,9\}$

4. Write a verbal description of the set $\{a, i, e, 0, u\}$

5. Is $\{1,3,5\}$ a subset of the set of odd integers?

6. Is $\{A, B, C\}$a subset of the set of letters of the alphabet?

For problems 7-12, consider the sets below, and indicate if each statement is true or false.

$A=\{1,2,3,4,5\} \quad B=\{1,3,5\} \quad C=\{4,6\} \quad U=\{\text { numbers from } 0 \text { to } 10\}$

7. $3 \in B$

8. $5 \in C$

9. $B \subset A$

10. $C \subset A$

11. $C \subset B$

12. $C \subset U$

Using the sets from above, and treating $U$ as the Universal set, find each of the following:

13. $A \cup B$

14. $A \cup C$

15. $A \cap C$

16. $B \cap C$

17. $A^{c}$

18. $B^{c}$

Let $D=\{b, a, c, k\}, \quad E=\{t, a, s, k\}, \quad F=\{b, a, t, h\}$. Using these sets, find the following:

19. $D^{c} \cap E$

20. $F^{c} \cap D$

21. $(D \cap E) \cup F$

22. $D \cap(E \cup P)$

23. $(F \cap E)^{c} \cap D$

24. $(D \cup E)^{c} \cap F$

Create a Venn diagram to illustrate each of the following:

25. $(F \cap E) \cup D$

26. $(D \cup E)^{c} \cap F$

27. $\left(F^{c} \cap E^{\prime}\right) \cap D$

28. $(D \cup E) \cup F$

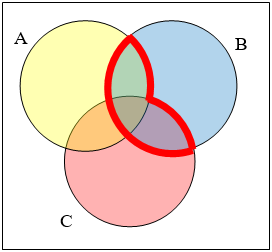
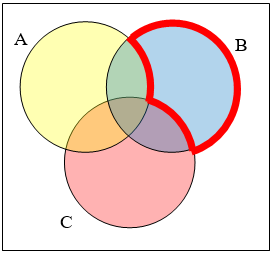
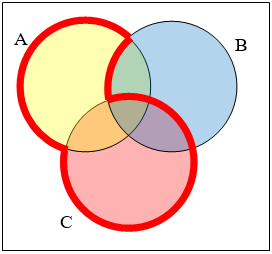
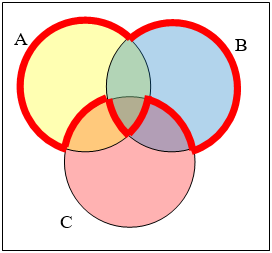
Write an expression for the shaded region.

29.

$A Venn diagram with 3 circles overlapping, labeled A, B, and C. The region where B overlaps either or both of the other sets is highlighted.$

30.

$A Venn diagram with 3 circles overlapping, labeled A, B, and C. The region in B alone is highlighted, where it isn't overlapping either other set.$

31.

$A Venn diagram with 3 circles overlapping, labeled A, B, and C. The highlighted region includes all of C, combined with the portion of A that doesn't overlap B.$

32.

$A Venn diagram with 3 circles overlapping, labeled A, B, and C. The highlighted region includes the part of A that doesn't overlap with C, combined with the part of B that doesn't overlap C, combined with the overlap of all three circles.$

Let $A=\{1,2,3,4,5\} \quad B=\{1,3,5\} \quad C=\{4,6\}$. Find the cardinality of the given set.

33. $\mathrm{n}(A)$

34. $\mathrm{n}(B)$

35. $\mathrm{n}(A \cup C)$

36. $\mathrm{n}(A \cap C)$

The Venn diagram here shows the cardinality of each set. Use this in 37-40 to find the cardinality of given set.

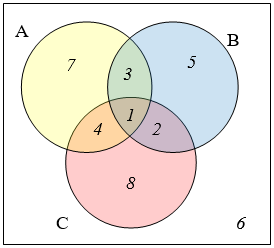
$A Venn diagram of three overlapping circles labeled A, B, and C. The part only in A is 7. The overlap of A and B only is 3. The part in B only is 5. The overlap of A and C only is 4. The overlap of all three is 1. The overlap of B and C only is 2. The part in C only is 8. The part outside all three is 6.$

37. $\mathrm{n}(A \cap C)$

38. $\mathrm{n}(B \cup C)$

39. $\mathrm{n}\left(A \cap B \cap C^{2}\right)$

40. $\mathrm{n}\left(A \cap B^{c} \cap C\right)$

41. If $n(G)=20, n(H)=30, n(G \cap H)=5,$ find $n(G \cup H)$

42. If $n(G)=5, n(H)=8, n(G \cap H)=4,$ find $n(G \cup H)$

43. A survey was given asking whether they watch movies at home from Netflix, Redbox, or a video store. Use the results to determine how many people use Redbox.

$\begin{array}{ll} \text{52 only use Netflix} & \text{62 only use Redbox} \\ \text{24 only use a video store} & \text{16 use only a video store and Redbox} \\ \text{48 use only Netflix and Redbox} & \text{30 use only a video store and Netflix} \\ \text{10 use all three} & \text{25 use none of these} \end{array}$

44. A survey asked buyers whether color, size, or brand influenced their choice of cell phone. The results are below. How many people were influenced by brand?

$\begin{array}{ll} \text{5 only said color} & \text{8 only said size} \\ \text{16 only said brand} & \text{20 said only color and size} \\ \text{42 said only color and brand} & \text{53 said only size and brand} \\ \text{102 said all three} & \text{20 said none of these} \end{array}$

45. Use the given information to complete a Venn diagram, then determine: a) how many students have seen exactly one of these movies, and b) how many had seen only Star Wars.

$\begin{array}{ll} \text{18 had seen The Matrix (M)} & \text{24 had seen Star Wars (SW)} \\ \text{20 had seen Lord of the Rings (LotR)} & \text{10 had seen M and SW} \\ \text{14 had seen LotR and SW } & \text{12 had seen M and LotR} \\ \text{6 had seen all three} & \text{} \end{array}$

46. A survey asked people what alternative transportation modes they use. Using the data to complete a Venn diagram, then determine: a) what percent of people only ride the bus, and b) how many people don’t use any alternate transportation.

$\begin{array}{ll} \text{30% use the bus} & \text{20% ride a bicycle} \\ \text{25% walk} & \text{5% use the bus and ride a bicycle} \\ \text{10% ride a bicycle and walk} & \text{12% use the bus and walk} \\ \text{2% use all three} & \text{} \end{array}$

Search

Text Color

Text Size

Margin Size

Font Type