16.2: Substitution Ciphers
- Page ID
- 34276
One simple encryption method is called a substitution cipher.
A substitution cipher replaces each letter in the message with a different letter, following some established mapping.
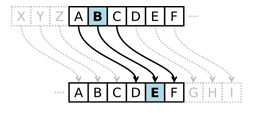A simple example of a substitution cipher is called the Caesar cipher, sometimes called a shift cipher. In this approach, each letter is replaced with a letter some fixed number of positions later in the alphabet. For example, if we use a shift of 3, then the letter A would be replaced with D, the letter 3 positions later in the alphabet. The entire mapping would look like: [1]
Original: \(\mathrm{ABCDEFGHIJKLMNOPQRSTUVWXYZ}\)
Maps to: \(\mathrm{DEFGHIJKLMNOPQRSTUVWXYZABC}\)
Use the Caesar cipher with shift of 3 to encrypt the message: “We ride at noon”
Solution
We use the mapping above to replace each letter. W gets replaced with Z, and so forth, giving the encrypted message: ZH ULGH DW QRRQ.
Notice that the length of the words could give an important clue to the cipher shift used. If we saw a single letter in the encrypted message, we would assume it must be an encrypted A or I, since those are the only single letters than form valid English words.
To obscure the message, the letters are often rearranged into equal sized blocks. The message ZH ULGH DW QRRQ could be written in blocks of three characters as
ZHU LGH DWQ RRQ.
Decrypt the message GZD KNK YDX MFW JXA if it was encrypted using a shift cipher with shift of 5.
Solution
We start by writing out the character mapping by shifting the alphabet, with A mapping to F, five characters later in the alphabet.
Original: \(\mathrm{ABCDEFGHIJKLMNOPQRSTUVWXYZ}\)
Maps to: \(\mathrm{FGHIJKLMNOPQRSTUVWXYZABCDE}\)
We now work backwards to decrypt the message. The first letter G is mapped to by B, so B is the first character of the original message. Continuing, our decrypted message is
BUY FIF TYS HAR ESA.
Removing spaces we get BUYFIFTYSHARESA. In this case, it appears an extra character was added to the end to make the groups of three come out even, and that the original message was “Buy fifty shares.”
Decrypt the message BNW MVX WNH if it was encrypted using a shift cipher with shift 9 (mapping A to J).
- Answer
-
SEND MONEY
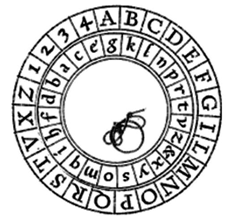
Notice that in both the ciphers above, the extra part of the alphabet wraps around to the beginning. Because of this, a handy version of the shift cipher is a cipher disc, such as the Alberti cipher disk shown here[2] from the 1400s. In a cipher disc, the inner wheel could be turned to change the cipher shift. This same approach is used for “secret decoder rings.”
The security of a cryptographic method is very important to the person relying on their message being kept secret. The security depends on two factors:
- The security of the method being used
- The security of the encryption key used
In the case of a shift cipher, the method is “a shift cipher is used.” The encryption key is the specific amount of shift used.
Suppose an army is using a shift cipher to send their messages, and one of their officers is captured by their enemy. It is likely the method and encryption key could become compromised. It is relatively hard to change encryption methods, but relatively easy to change encryption keys.
During World War II, the Germans’ Enigma encryption machines were captured, but having details on the encryption method only slightly helped the Allies, since the encryption keys were still unknown and hard to discover. Ultimately, the security of a message cannot rely on the method being kept secret; it needs to rely on the key being kept secret.
The security of any encryption method should depend only on the encryption key being difficult to discover. It is not safe to rely on the encryption method (algorithm) being kept secret.
With that in mind, let’s analyze the security of the Caesar cipher.
Suppose you intercept a message, and you know the sender is using a Caesar cipher, but do not know the shift being used. The message begins EQZP. How hard would it be to decrypt this message?
Solution
Since there are only 25 possible shifts, we would only have to try 25 different possibilities to see which one produces results that make sense. While that would be tedious, one person could easily do this by hand in a few minutes. A modern computer could try all possibilities in under a second.
\(\begin{array}{|l|l|l|l|l|l|l|l|}
\hline \textbf { Shift } & \textbf { Message } & \textbf { Shift } & \textbf { Message } & \textbf { Shift } & \textbf { Message } & \textbf { Shift } & \textbf { Message } \\
\hline 1 & \text { DPYO } & 7 & \text { XJSI } & 13 & \text { RDMC } & 19 & \text { LXGW } \\
\hline 2 & \text { COXN } & 8 & \text { WIRH } & 14 & \text { QCLB } & 20 & \text { KWFV } \\
\hline 3 & \text { BNWM } & 9 & \text { VHQG } & 15 & \text { PBKA } & 21 & \text { JVEU } \\
\hline 4 & \text { AMVL } & 10 & \text { UGPF } & 16 & \text { OAJZ } & 22 & \text { IUDT } \\
\hline 5 & \text { ZLUK } & 11 & \text { TFOE } & 17 & \text { NZIY } & 23 & \text { HTCS } \\
\hline 6 & \text { YKTJ } & \mathbf{1 2} & \textbf { SEND } & 18 & \text { MYHX } & 24 & \text { GSBR } \\
\hline & & & & & & 25 & \text { FRAQ } \\
\hline
\end{array}\)
In this case, a shift of 12 (A mapping to M) decrypts EQZP to SEND. Because of this ease of trying all possible encryption keys, the Caesar cipher is not a very secure encryption method.
A brute force attack is a method for breaking encryption by trying all possible encryption keys.
To make a brute force attack harder, we could make a more complex substitution cipher by using something other than a shift of the alphabet. By choosing a random mapping, we could get a more secure cipher, with the tradeoff that the encryption key is harder to describe; the key would now be the entire mapping, rather than just the shift amount.
Use the substitution mapping below to encrypt the message “March 12 0300”
Original: \(mathrm{ABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789}\)
Maps to: \(\mathrm{2BQF5WRTD8IJ6HLCOSUVK3A0X9YZN1G4ME7P}\)
Solution
Using the mapping, the message would encrypt to 62SQT ZN Y1YY
Use the substitution mapping from Example 4 to decrypt the message C2SVX2VP
- Answer
-
PARTY AT 9
While there were only 25 possible shift cipher keys (35 if we had included numbers), there are about 1040 possible substitution ciphers[3]. That’s much more than a trillion trillions. It would be essentially impossible, even with supercomputers, to try every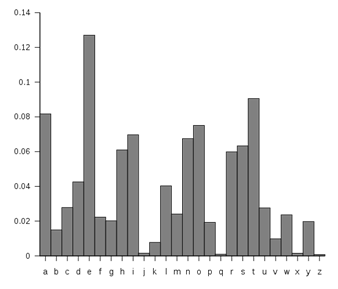 
possible combination. Having a huge number of possible encryption keys is one important part of key security.
Unfortunately, this cipher is still not secure, because of a technique called frequency analysis, discovered by Arab mathematician Al-Kindi in the 9th century. English and other languages have certain letters than show up more often in writing than others.[4] For example, the letter E shows up the most frequently in English. The chart to the right shows the typical distribution of characters.
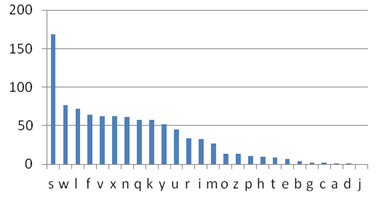The chart to the right shows the frequency of different characters in some encrypted text. What can you deduce about the mapping?
Solution
Because of the high frequency of the letter S in the encrypted text, it is very likely that the substitution maps E to S. Since W is the second most frequent character, it likely that T or A maps to W. Because C, A, D, and J show up rarely in the encrypted text, it is likely they are mapped to from J, Q, X, and Z.
In addition to looking at individual letters, certain pairs of letters show up more frequently, such as the pair “th.” By analyzing how often different letters and letter pairs show up an encrypted message, the substitution mapping used can be deduced[5].
[1] en.Wikipedia.org/w/index.php?title=File:Caesar3.svg&page=1. PD
[2] en.Wikipedia.org/wiki/File:Alberti_cipher_disk.JPG
[3] There are 35 choices for what A maps to, then 34 choices for what B maps to, and so on, so the total number of possibilities is 35*34*33*…*2*1 = 35! = about 1040
[4] en.Wikipedia.org/w/index.php?title=File:English_letter_frequency_(alphabetic).svg&page=1 PD
[5] For an example of how this is done, see en.Wikipedia.org/wiki/Frequency_analysis