5.2: Borders on a Square
( \newcommand{\kernel}{\mathrm{null}\,}\)
Here’s another problem:
Here is a large square made up of 100 smaller unit squares. The unit squares along the border of the large square are colored red. Without counting one-by-one, can you figure out how many red squares there are in the picture?
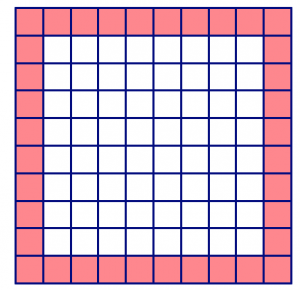
Clearly describe how you figured out the number of red squares, and how you know your answer is correct.
Justin calculated the number of squares as (10×4)−4. He justified his answer this way:
Since the dimensions of the big square are 10×10, there are 10 squares along each of the four sides. So that gives me 40 red squares. But then each corner is part of two different sides. I’ve counted each of the corners twice. So I need to make up for that by subtracting 4 at the end.
Justin showed this picture to justify his work:
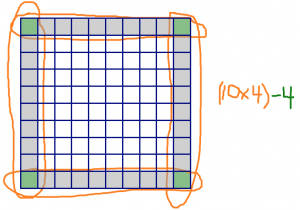
- What do you think about Justin’s solution? Are you convinced? Could he have explained it more clearly?
- Was Justin’s solution different from your solution or the same?
- Notice the color coding in Justin’s picture. What do the colors represent? Why did he use the colors the way he did?
There are lots of different ways to calculate the number of colored squares along the border of a 10×10 square. Below are the calculations several other students did. For each calculation, write a justification and draw a picture to show why it calculates the number of squares correctly. Think about using color in your picture to make your work more clear.
- Valerie calculated 10+10+8+8.
- Kayla calculated 4×9.
- Linda calculated (10×10)−(8×8).
- Mark calculated (4×8)+4.
- Allan calculated 10+9+9+8.
Now suppose that you have a large 6×6 square with the unit squares along the border colored red. Adapt two of the techniques above to calculate the number of red unit squares.
For each technique you used, write an explanation and include a picture. Think about how to use colors or other methods to make your picture and explanation more clear.
Now suppose that you have a large 25×25 square with the unit squares along the border colored red. Adapt two of the techniques above to calculate the number of red unit squares.
For each technique you used, write an explanation and include a picture. Think about how to use colors or other methods to make your picture and explanation more clear.
- Suppose that you have 64 red squares. Can you use all of those squares to make the border of a larger square in a picture like the one above? If yes, what are the dimensions of the larger square? If no, why not?
- What if you have 30 red squares? Same questions.
- What if you have 256 red squares? Same questions.
Describe some general rules:
- If you have a large n×n square with the border squares colored red, how many red squares will there be? Justify your answer with words and a picture.
- If you have
red squares, is there a quick test you can do to decide if you can use all of those squares to make the border of a large square? Can you tell how big the square will be?


