2.2: Addition, Subtraction, and Scalar Multiplication of Vectors

Last updated
Save as PDF

Page ID: 125029

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Addition and Subtraction of Vectors

To add or subtract two vectors, add, or subtract their corresponding components.

Example $\PageIndex{1}$

To ADD the vectors $\vec{u}$ and $\vec{v}$

Solution

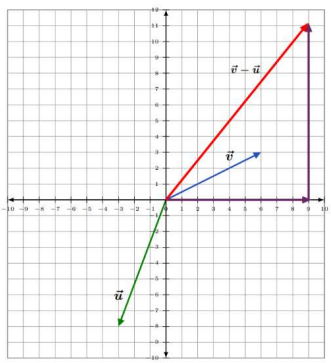
To ADD the vectors $\vec{u}$ and $\vec{v}$, begin by writing each in component form.

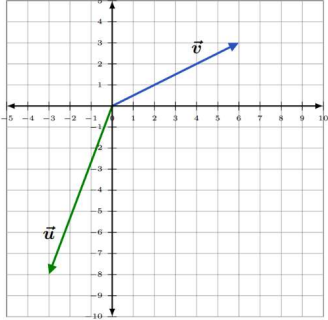
$This image shows the starting points of the two vectors v and u connected together at (0,0), but pointing in different directions. The terminal point for vector v (6,3) and for u, the terminal point if (negative 3,8).$

$\vec{u}=\langle-3,-8\rangle \text { and } \vec{v}=\langle 6,3\rangle$

ADD their corresponding components

$\vec{u}+\vec{v}=\langle-3+6,-8+3\rangle=\langle 3,-5\rangle$

So, $\vec{u}+\vec{v}=\langle 3,-5\rangle$

Now, graph this sum.

Start at the origin.
Since the horizontal component is 3, move 3 units to the right.
Since the vertical component is −5 , move 5 units downward.

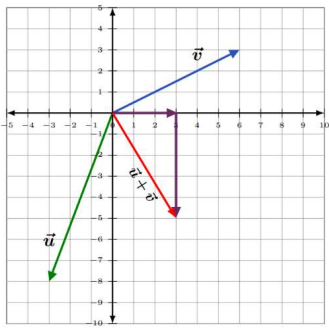
$Image of two vectors and a demonstration of graphing their sum. Here are the same vectors v and u. There is a third vector in between called u + v. The starting points for all of the three vectors is (0,0). The ending point of vector v is (6,3), the ending point for vector u is (negative 3, negative 8). The ending point of u + v is (3, negative 5).$

The addition of two vectors $\vec{u}$ and $\vec{v}$ can be demonstrated by placing the tail of one vector at the head of the other. Then connect the tail of $\vec{u}$ to the head of $\vec{v}$.

$Image of the same vectors v and u showing a different example of graphing their sum. Vector u has the same starting point (0,0) and ending point (negative 3, negative 8). But the tail of vector v is now at (negative 3, negative 8) and the head is at (3, negative 5). Drawing a line from the tail of vector u at (0,0) to the head of vector v at (3, negative 5), gives you the vector u + v.$

Example $\PageIndex{2}$

To SUBTRACT the vector $\vec{u}$ from the vector $\vec{v}$

Solution

To SUBTRACT the vector $\vec{u}$ from the vector $\vec{v}$, begin by writing each in component form.

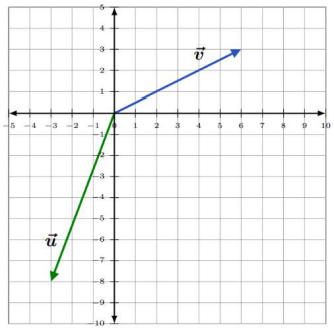
$Image of two vectors v and u pointing in different directions with the same starting point at (0,0). The terminal point of vector v is (6,3) and the terminal point of vector u is ( negative 3, negative 8).$

$\vec{u}=\langle-3,-8\rangle$ and $\vec{v}=\langle 6,3\rangle$

SUBTRACT the components of $\vec{u}$ from the corresponding components of $\vec{v}$

$\vec{v}-\vec{u}=\langle 6-(-3), 3-(-8)\rangle=\langle 6+3,3+8\rangle=\langle 9,11\rangle$

So, $\vec{v}-\vec{u}=\langle 9,11\rangle$

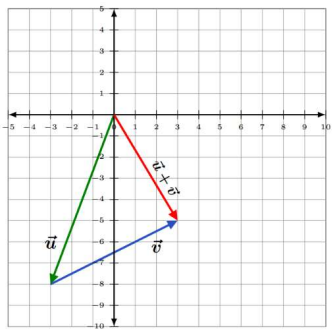
Now, graph this sum.

Start at the origin.
Since the horizontal component is 9, move 9 units to the right.
Since the vertical component is 11, move 11 units upward.

$Image of vectors v and u and an example of graphing their subtraction which produces vector v - u. The starting point of vector v - u is (0,0) and the terminal point is (9,11).$

Scalars

Definition: Scalar

In contrast to a vector, and having both direction and magnitude, a SCALAR is a physical quantity defined by only its magnitude.

Examples are speed, time, distance, density, and temperature. They are represented by real numbers (both positive and negative), and they can be operated on using the regular laws of algebra.

The term scalar derives from this usage: a scalar is that which scales, resizes a vector.

Scalar multiplication is the multiplication of a vector by a real number (a scalar).

Suppose we let the letter $k$ represent a real number and $\vec{v}$ be the vector $\left\langle x\right.,\left.y\right\rangle .$ Then, the scalar multiple of the vector $\vec{v}$ is

$k \vec{v}=\langle k x, k y\rangle$

To multiply a vector by a scalar (a constant), multiply each of its components by the constant.

$This image shows the different scalars of v. First there is v. Then there is 2v, which is twice as long as v. Finally, there is (negative one half)v, which is half as long as v. The negative sign in (negative one half) v makes it face in the opposite direction as v.$

Suppose $\overrightarrow{u}=\left\langle -3,\left.-8\right\rangle \right.$ and $k=3$. Then \[k\overrightarrow{u}=3\overrightarrow{u}=3\left\langle -3,\left.-8\right\rangle \right.=\left\langle 3(-3),\left.3(-8)\right\rangle \right.=\left\langle -9,\left.-24\right\rangle \right. \nonumber \]
Suppose $\overrightarrow{v}=\left\langle 6,\left.3\right\rangle \right.$ and $k=\frac{-1}{3}$. Then \[k \vec{u}=\frac{-1}{3} \vec{u}=\frac{-1}{3}\langle 6,3\rangle=\left\langle\frac{-1}{3}(6), \frac{-1}{3}(3)\right\rangle=\langle-2,-1\rangle \nonumber \]
Suppose $\overrightarrow{u}=\left[ \begin{array}{c} -2 \\ 6 \end{array} \right]$ and $\overrightarrow{v}=\left[ \begin{array}{c} 5 \\ 3 \end{array} \right]$. Then \[3\overrightarrow{u}+4\overrightarrow{v}=3\left[ \begin{array}{c} -2 \\ 6 \end{array} \right]+4\left[ \begin{array}{c} 5 \\ 3 \end{array} \right]=\left[ \begin{array}{c} -6 \\ 18 \end{array} \right]+\left[ \begin{array}{c} 20 \\ 12 \end{array} \right]=\left[ \begin{array}{c} 14 \\ 30 \end{array} \right] \nonumber \]

Using Technology

We can use technology to add and subtract vectors and to multiply a vector by a scalar.

Go to www.wolframalpha.com.

For the vectors $\overrightarrow{u}=\left[ \begin{array}{c} -2 \\ 6 \end{array} \right]$ and $\overrightarrow{v}=\left[ \begin{array}{c} 5 \\ 3 \end{array} \right]$, use WolframAlpha to find $3\overrightarrow{u}+4\overrightarrow{v}$. Enter evaluate 3$\mathrm{<}$-2, 6$\mathrm{>}$ + 4$\mathrm{<}$5, 3$\mathrm{>}$ in the entry field. Wolframalpha tells you what it thinks you entered, then tells you its answer. In this case, $<14,\ 30>$.

This screenshot from WolframAlpha shows vector addition with scalar multiplication. You are adding the vector <negative 2,6 multiplied by 3 and <5,3> multiplied by 4. The result is the vector <14,30>." src="/@api/deki/files/97350/clipboard_eaf3e6c7b171f693605d899d7edbd53b1.png">

Try These

Exercise $\PageIndex{1}$

Find the sum of the two vectors $\vec{u}=\langle-5,2\rangle$ and $\vec{v}=\langle 10,-1\rangle$.

Answer: $\overrightarrow{u}\ +\ \overrightarrow{v}=\left\langle -5,\left.1\right\rangle \right.$

Exercise $\PageIndex{2}$

Subtract the vector $\vec{u}=\langle-5,2\rangle$ from the vector $\vec{v}=\langle 10,-1\rangle$

Answer: $\overrightarrow{v}-\ \overrightarrow{u}=\left\langle 15,\left.-3\right\rangle \right.$

Exercise $\PageIndex{3}$

Suppose $\vec{u}=\langle-5,2\rangle, \vec{v}=\langle 1,6\rangle$, and $\vec{w}=\langle 4,-3\rangle$. Perform the operation $2 \vec{u}-4 \vec{v}+3 \vec{w}$.

Answer: $\langle -29,-5\rangle$

Search

Example \(\PageIndex{1}\)

Solution

Example \(\PageIndex{2}\)

Solution

Definition: Scalar

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)