2.3: Magnitude, Direction, and Components of a Vector
- Page ID
- 125030
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
The Magnitude of a Vector
It is productive to represent the horizontal and vertical components of a vector \(\vec{v}\) as \(v_x\) and \(v_y\), respectively.
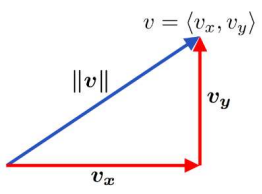
The magnitude (the length) of a vector \(\vec{v}=\left\langle v_x, v_y\right\rangle\) is \[\|\vec{v}\|=\sqrt{v_x^2+v_y^2} \nonumber \]
Magnitude of vector \(\vec{v}=\left\langle 5,\left.-8\right\rangle \right.\):

Solution
The vector \(\vec{v}=\left\langle 5,\left.-8\right\rangle \right.\) has magnitude:
\(\left\|\overrightarrow{v}\right\|=\sqrt{{v_x}^2+{v_y}^2}\)= \(\sqrt{5^2+{\left(-8\right)}^2}=\ \sqrt{25+64}\) = \(\sqrt{89}\)
Interpret this as the length of the vector \(\overrightarrow{v}=\left\langle 5,\left.-8\right\rangle \right.\) is \(\sqrt{89}\) units.
The Direction of a Vector
The direction of a vector \(\vec{v}\) is the angle the vector makes with the positive x-axis.
It is typically represented with the uppercase Greek letter theta \(\theta\). We use some trigonometry to determine the angle \(\theta\).

\(\tan \theta=\dfrac{y}{x}\) or \(\theta=\tan ^{-1} \dfrac{y}{x}\)
The angle \(\theta \) is always between \(0^{\circ}\) and \(360^{\circ}\).
To approximate the direction of the vector \(\vec{v}=\langle 5,8\rangle\), use \(\theta=\tan ^{-1} \frac{y}{x}\), with \(x=5\) and \(y=8\).
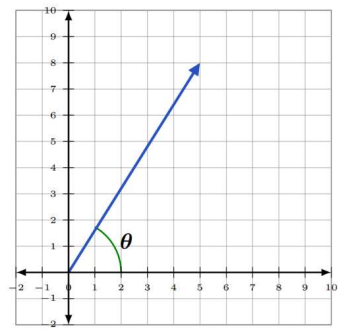
Solution
\(\begin{aligned}
\vec{v} & =\langle 5,8\rangle \\
\theta & =\tan ^{-1} \frac{y}{x} \\
\theta & =\tan ^{-1} \frac{8}{5}
\end{aligned}\)
Using a calculator, we get
\(\begin{aligned}
& \theta=57.99^{\circ} \\
& \theta=58^{\circ}
\end{aligned}\)
To approximate the direction of the vector \(\vec{v}=\langle 5,-8\rangle\), use \(\theta=\tan ^{-1} \frac{y}{x}\), with \(x=5\) and \(y=-8\).

Solution
\(\begin{gathered}
\vec{v}=\langle 5,-8\rangle \\
\theta=\tan ^{-1} \frac{y}{x} \\
\theta=\tan ^{-1} \frac{-8}{5}
\end{gathered}\)
Using a calculator, we get
\(\theta=-57.99^{\circ}\)
Vertical component is in Quadrant IV and \(\theta\) must be in the interval \(\left[0,\left.360\right)\right.\), therefore we calculate \(\theta\) by
\[\theta =360{}^\circ -57.99{}^\circ =302.005{}^\circ\nonumber \] \[\theta =302{}^\circ \nonumber \]
The Components of a Vector
The lengths of the \(x\)- and \(y\)- components of a vector \(\left\|\vec{v}\right\|=\sqrt{{v_x}^2+{v_y}^2}\) in two dimensions can be found using trigonometric ratios.
\(\vec{v}_x=\|\vec{v}\|_{\cos \theta}\)and \(\vec{v}_y=\|\vec{v}\|_{\sin \theta}\)
\(\vec{v}_x\) is the horizontal component of \(\vec{v}\) and \(\vec{v}_y\) is the vertical component.
The angle \(\theta\) is always between \(0^{\circ}\) and \(360^{\circ}\).
Suppose the magnitude of a vector \(\vec{v}\boldsymbol{=}\left\langle v_x,\left.v_y\right\rangle \right.\) is 20 units, and that \(\vec{v}\) makes a 60\(\mathrm{{}^\circ}\) angle with the horizontal. Then, the components of \(\vec{v}\) are
\[\begin{aligned}
\vec{v}_x & =\|\vec{v}\| \cos \theta \\
= & 20 \cos 60^{\circ} \\
& =20 \cdot \frac{1}{2} \\
& =10
\end{aligned} \nonumber \]
and
\[\begin{aligned}
\vec{v}_y & =\|\vec{v}\|_{\sin } \theta \\
= & 20 \sin 60^{\circ} \\
& =20 \cdot \frac{\sqrt{3}}{2} \\
& =10 \sqrt{3}
\end{aligned} \nonumber \]
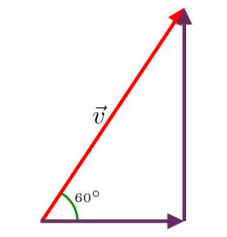
So, we could write \(\vec{v}\boldsymbol{=}\left\langle v_x,\left.v_y\right\rangle \right.\) as \(\vec{v}\boldsymbol{=}\left\langle 10,\left.10\sqrt{3}\right\rangle \right.\)
Using Technology
We can use technology to determine the magnitude of a vector.
Go to www.wolframalpha.com.
To find the magnitude of the vector \(\vec{v}\boldsymbol{=}\left\langle 2,\left.4\right\rangle ,\right.\) enter magnitude of the vector \(\mathrm{<}\)2,4\(\mathrm{>}\) in the entry field. Wolframalpha tells you what it thinks you entered, then tells you its answer. In this case, \(\left\|\vec{v}\right\|=2\sqrt{5}\).
. The result is 2 times the square root of 5." src="/@api/deki/files/97361/clipboard_e757f835523c600e69c47a6190429dff2.png">
To find the direction of the vector \(\vec{v}\boldsymbol{=}\left\langle 5,\left.8\right\rangle ,\right.\) enter direction of the vector \(\mathrm{<}\)5,8\(\mathrm{>}\) in the entry field. Wolframalpha answers \(57.9946{}^\circ \approx 58{}^\circ\).
. The result is 9.43398 radians (r) and 57.9946 degrees from the x-axis (theta)." src="/@api/deki/files/97362/clipboard_e0ddb516d9c06e26d0792e439e307323d.png">
Try These
Find the magnitude of the vector \(\vec{v}=\langle 3,-4\rangle\).
- Answer
-
\(\left\|\overrightarrow{v}\right\|=5\)
Find the magnitude of the vector \(\vec{v}=\langle -3,-3\rangle\).
- Answer
-
\(\left\|\overrightarrow{v}\right\|=3\sqrt{2}\)
Find the components of the vector \(\vec{v}\) if the magnitude of \(\vec{v}\) is 6 and it makes a \(30^{\circ}\) angle with the horizontal.
- Answer
-
\({\overrightarrow{v}}_x=\ 3\sqrt{3}\) and \({\overrightarrow{v}}_y\mathrm{=3}\)
Approximate the direction of the vector \(\vec{v}=\langle 3,10\rangle\).
- Answer
-
\(\theta \approx 73.3008{}^\circ\)

