4.3: Matrix Multiplication
- Page ID
- 125045
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Compatible Matrices
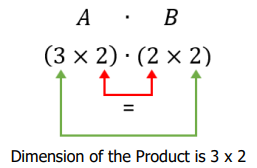
We are going to multiply together two matrices, one of size \(m\times n\), and one of size \(n\times p\). The multiplication will be possible, and the product exists because the sizes make them compatible with each other.

Notice the number of columns of the leftmost matrix is equal to the number of rows of the rightmost matrix.
For the product, \(A \cdot B\), of two matrices to exist it must be that (the number of columns of matrix \(A\) ) = (the number of rows of matrix \(B\)) Matrices for which this is true are said to be compatible with each other.
Matrices as Collections of Row and Column Matrices
It is productive to think of a matrix as a collection of individual row matrices and column matrices.For example, we can think of the matrix \(A=\left[ \begin{array}{cc} 3 & 1 \\ --4 & 2 \\ 0 & 5 \end{array} \right]\) as being composed of
- the three row matrices, \(\left[ \begin{array}{cc} 3 & 1 \end{array} \right],\ \ \left[ \begin{array}{cc} --4 & 2 \end{array} \right],\) and \(\left[ \begin{array}{cc} 0 & 5 \end{array} \right],\ \)and
- the two column matrices \(\left[ \begin{array}{c} 3 \\ --4 \\ 0 \end{array} \right]\) and \(\left[ \begin{array}{c} 1 \\ 2 \\ 5 \end{array} \right]\).
(If you need a review of row and column matrices, see Section 4.2)
Multiplication of Two Matrices
To multiply two compatible matrices \(A\) and \(B\) together, multiply every row matrix of \(A\) through every column matrix of \(B\).
Suppose the size of matrix \(A\) is \(3\times 4\) and the size of matrix \(B\) is \(4\times 5\). The matrices are compatible with each other and the size of the product is \(3\times 5\)
Some of the entries of the product \(A\bullet B\) are
\(a_{11}\): The entry in row 1, column 1, is the result of multiplying the
1st row of matrix \(A\) through the 1st column of matrix \(B\).
\(a_{12}\): The entry in row 1, column 2, is the result of multiplying the
1st row of matrix \(A\) through the 2nd column of matrix \(B\).
\(a_{24}\): The entry in row 2, column 4, is the result of multiplying the
2nd row of matrix \(A\) through the 4th column of matrix \(B\).
\(a_{35}\): The entry in row 3, column \(5\), is the result of multiplying the
3rd row of matrix \(A\) through the 5th column of matrix \(B\).
\(a_{33}\): The entry in row 3, column 3, is the result of multiplying the
3rd row of matrix \(A\) through the 3rd column of matrix \(B\).
Do you see the general rule for producing any particular entry?
To get the entry in row \(i\) and column\(\ j\), \(a_{ij},\ \)multiply
the \(ith\) row of matrix \(A\) through the \(jth\) column of matrix \(B.\)
Compute the product of the matrices \(A=\left[ \begin{array}{cc} 3 & 1 \\ --4 & 2 \\ 0 & 5 \end{array} \right]\) and \(B=\left[ \begin{array}{cc} 3 & 2 \\ 4 & 1 \end{array} \right]\).
First note that the two matrices are compatible
Solution
\[A \cdot B=\left[\begin{array}{cc}
3 & 1 \\
-4 & 2 \\
0 & 5
\end{array}\right] \cdot\left[\begin{array}{ll}
3 & 2 \\
4 & 1
\end{array}\right] \nonumber \]
The product is the \(3\times 2\) matrix of the form \(\left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{array} \right]\)
Since we are multiplying 3 rows through 2 columns, there will be 6 entries. The six entries of \(A\bullet B\) are
\(a_{11}=\ \)the 1st row of \(A\) times the 1st column of \(B\)
\[=\left[\begin{array}{ll}
3 & 1
\end{array}\right] \cdot\left[\begin{array}{l}
3 \\
4
\end{array}\right]=[3 \cdot 3+1 \cdot 4]=[13] \nonumber \]
\(a_{12}=\ \)the 1st row of \(A\) times the 2nd column of \(B\)
\[=\left[\begin{array}{ll}
3 & 1
\end{array}\right] \cdot\left[\begin{array}{l}
2 \\
1
\end{array}\right]=[3 \cdot 2+1 \cdot 1]=[7] \nonumber \]
\(a_{21}=\ \)the 2nd row of \(A\) times the 1st column of \(B\)
\[=\left[\begin{array}{ll}
-4 & 2
\end{array}\right] \cdot\left[\begin{array}{l}
3 \\
4
\end{array}\right]=[-4 \cdot 3+2 \cdot 4]=[-4] \nonumber \]
\(a_{22}=\ \)the 2nd row of \(A\) times the 2nd column of \(B\)
\[=\left[\begin{array}{ll}
-4 & 2
\end{array}\right] \cdot\left[\begin{array}{l}
2 \\
1
\end{array}\right]=[-4 \cdot 2+2 \cdot 1]=[-6] \nonumber \]
\(a_{31}=\ \)the 3rd row of \(A\) times the 1st column of \(B\)
\[=\left[\begin{array}{ll}
0 & 5
\end{array}\right] \cdot\left[\begin{array}{l}
3 \\
4
\end{array}\right]=[0 \cdot 3+5 \cdot 4]=[20] \nonumber \]
\(a_{32}=\) the 3rd row of \(A\) times the 2nd column of \(B\)
\[=\left[\begin{array}{ll}
0 & 5
\end{array}\right] \cdot\left[\begin{array}{l}
2 \\
1
\end{array}\right]=[0 \cdot 2+5 \cdot 1]=[5] \nonumber \]
So, \(A \cdot B=\left[\begin{array}{cc}
13 & 7 \\
-4 & -6 \\
20 & 5
\end{array}\right]\)
Your Turn: Show that the product of the matrices \(A\mathrm{=}\left[ \begin{array}{cc} \mathrm{2} & \mathrm{3} \\ \mathrm{4} & \mathrm{1} \end{array} \right]\) and \(B\mathrm{=}\left[ \begin{array}{ccc} \mathrm{2} & \mathrm{3} & 0 \\ \mathrm{1} & \mathrm{2} & \mathrm{4} \end{array} \right]\) is \(\left[ \begin{array}{ccc} \mathrm{7} & \mathrm{12} & \mathrm{12} \\ \mathrm{9} & \mathrm{14} & \mathrm{4} \end{array} \right]\).
Using Technology
You can see that multiplying matrices together involves a lot of arithmetic and can be cumbersome. We can use technology to help us through the process.
Go to www.wolframalpha.com.
To find the product of the two matrices of above Your Turn Example, enter [[2,3], [4,1]] * [[2,3,0], [1,2,4]] in the entry field. WolframAlpha sees a matrix as a collection of row matrices.

Both entries and rows are separated by commas and WA does not see spaces.
Wolframalpha tells you what it thinks you entered, then tells you its answer \(\left[ \begin{array}{ccc} 7 & 12 & 12 \\ 9 & 14 & 4 \end{array} \right]\).
![This screenshot from WolframAlpha shows a matrix multiplication of a 2 x 2 matrix and a 2 x 3 matrix. The equation is [[2,3],[4,1]] * [[2,3,0],[1,2,4]]. The result is a matrix with the first row of 7 12 12 and a second row of 9 14 4.](https://math.libretexts.org/@api/deki/files/97501/clipboard_e3239e8b46cfdaf1b1c18aa1e4cc3265b.png?revision=1)
Try these
\[A=\left[\begin{array}{cc}
1 & 2 \\
-1 & 3 \\
0 & 4
\end{array}\right] \quad B=\left[\begin{array}{cc}
3 & 2 \\
1 & 0 \\
-1 & -2
\end{array}\right] \quad C=\left[\begin{array}{lll}
2 & 1 & 3 \\
4 & 2 & 1
\end{array}\right] \quad D=\left[\begin{array}{cc}
-2 & 6 \\
4 & 1
\end{array}\right] \quad E=\left[\begin{array}{l}
5 \\
2
\end{array}\right] \quad F=\left[\begin{array}{l}
2 \\
1 \\
5
\end{array}\right] \nonumber \]
\(A \cdot C\)
- Answer
-
\(\left[ \begin{array}{ccc} 10 & 5 & 5 \\ 10 & 5 & 0 \\ 16 & 8 & 4 \end{array} \right]\)
\(C \cdot A\)
- Answer
-
\(\left[ \begin{array}{cc} 1 & 19 \\ 2 & 18 \end{array} \right]\)
Compare your answers to question 1 and 2. If you got them right, would you say that matrix multiplication is or is not commutative?
- Answer
-
Is not commutative
\(D \cdot C\)
- Answer
-
\(\left[ \begin{array}{ccc} 20 & 10 & 0 \\ 12 & 6 & 13 \end{array} \right]\)
\(C \cdot F\)
- Answer
-
\(\left[ \begin{array}{c} 20 \\ 15 \end{array} \right]\)
\(A \cdot E\)
- Answer
-
\(\left[ \begin{array}{c} 9 \\ 1 \\ 8 \end{array} \right]\)
\(D^2\)
- Answer
-
\(\left[ \begin{array}{cc} 28 & -6 \\ -4 & 25 \end{array} \right]\)
\(D \cdot\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
- Answer
-
\(D\)
\(B \cdot D\)
- Answer
-
\(\left[ \begin{array}{cc} 2 & 20 \\ -2 & 6 \\ -6 & -8 \end{array} \right]\)
\(B \cdot D \cdot C\)
- Answer
-
\(\left[ \begin{array}{ccc} 84 & 42 & 26 \\ 20 & 10 & 0 \\ -44 & -22 & -26 \end{array} \right]\)
\(D \cdot B\)
- Answer
-
Not defined

