5.1: The Basic Trigonometric Functions

Right Triangle Trigonometry

There are six trigonometric functions associated with right triangles. Since our focus is on the mathematics of games, we will concentrate on only three of them, the sine function, the cosine function, and the tangent function.

The sine function is useful for producing the vertical motion of an object and the cosine function for producing the horizontal motion.

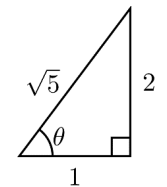
The figures just below show right triangles with angle \(\theta\), and sides opposite angle \(\theta\), adjacent to angle \(\theta\), and the hypotenuse of the triangle\(.\)

The angle \(\theta\) has two measures associated with it:

1. Its degree measure, which we can label \(\theta {}^\circ\), and
2. Its trigonometric measure.

A trigonometric measure of an angle is a ratio (quotient) of two of the sides of the triangle.

We will discuss all three of these ratios, the sine, the cosine, and the tangent of an angle.

The Sine of an Angle

Definition: Sine of an Angle

In words: In a right triangle, the sine of angle \(\theta\) is the ratio of the length of the side opposite \(\theta\) to the length of the hypotenuse. We abbreviate the phrase “the sine of angle \(\theta\)” with \(\sin \theta\).

\[\sin \theta=\frac{\text { opposite }}{\text { hypotenuse }} \nonumber \]

\[\sin \theta=\frac{y}{r} \nonumber \]

The Cosine of an Angle

Definition: Cosine of an Angle

In words: In a right triangle, the cosine of angle \(\theta\) is the ratio of the length of the side adjacent to \(\theta\) to the length of the hypotenuse. We abbreviate the phrase “the cosine of angle \(\theta\)” with \(\cos \theta\).

\[\cos \theta=\frac{\text { adjacent }}{\text { hypotenuse }} \nonumber \]

\[\cos \theta=\frac{x}{r} \nonumber \]

The Tangent of an Angle

Definition: Tangent of an Angle

In words: In a right triangle, the tangent of angle \(\theta\) is the ratio of the length of the side opposite \(\theta\) to the length of the side adjacent to \(\theta\). We abbreviate the phrase “the tangent of angle \(\theta\)” with \(\tan \theta\).

\[\tan \theta=\frac{\text { opposite }}{\text { adjacent }} \nonumber \]

\[\tan \theta=\frac{y}{x} \nonumber \]

Example \(\PageIndex{1}\)

Find \(\sin \theta \), \(\cos \theta \) and \(\tan \theta\) for the 3-4-5 triangle.

Solution

\(\begin{aligned}
& \sin \theta=\frac{\text { opposite }}{\text { hypotenuse }}=\frac{3}{5}=0.6 \\
& \cos \theta=\frac{\text { adjacent }}{\text { hypotenuse }}=\frac{4}{5}=0.8 \\
& \tan \theta=\frac{\text { opposite }}{\text { adjacent }}=\frac{3}{4}=0.75
\end{aligned}\)

Example \(\PageIndex{2}\)

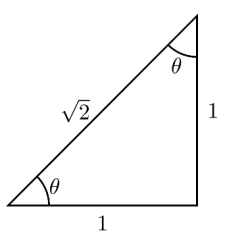
Find \(\sin \theta \), \(\cos \theta \), and \(\tan \theta\) for the triangle.

Solution

\(\begin{aligned}
&\sin \theta=\frac{\text { opposite }}{\text { hypotenuse }}=\frac{1}{\sqrt{2}} \approx 0.7071\\
&\begin{aligned}
& \cos \theta=\frac{\text { adjacent }}{\text { hypotenuse }}=\frac{1}{\sqrt{2}} \approx 0.7071 \\
& \tan \theta=\frac{\text { opposite }}{\text { adjacent }}=\frac{1}{1}=1
\end{aligned}
\end{aligned}\)

Using Technology

WolframAlpha evaluates the sines, cosines, and tangents of angles for us.

Go to www.wolframalpha.com.

Example \(\PageIndex{3}\)

Find \(\sin 45^{\circ}\), \(\cos 45^{\circ}\), and \(\tan 45^{\circ}\).

Solution

To compute these ratios, enter Evaluate sin(45), cos(45), tan(45) into the entry field.

Separate the entries with commas. WA does not see spaces.

WolframAlpha tells you what it thinks you entered, then tells you its answers.

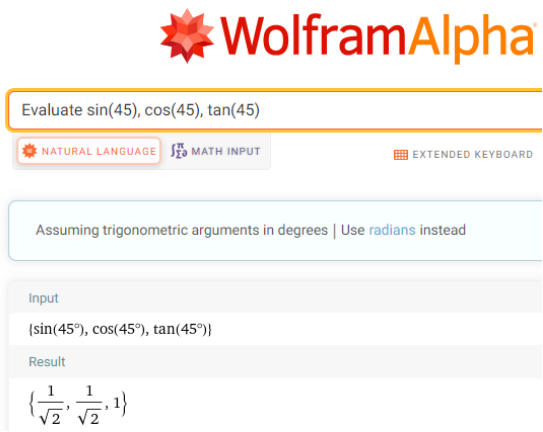
We conclude that \(\sin 45^{\circ}=\frac{1}{\sqrt{2}}\), \(\cos 45^{\circ}=\frac{1}{\sqrt{2}}\) , and \(\tan 45^{\circ}=1\).

WA also provides us with decimal approximations to these ratios.

\(\sin 45^{\circ}=0.7070107, \cos 45^{\circ}=0.7070107\), and \(\tan 45^{\circ}=1\)

Notice that these are the same values we got in Example 2.

Example \(\PageIndex{4}\)

Find \(\sin 30^{\circ}\), \(\sin 60^{\circ}\), \(\sin 90^{\circ}\).

Solution

To compute these ratios, enter Evaluate sin(30), sin(60), sin(90) into the entry field.

Separate the entries with commas. WA does not see spaces.

WolframAlpha tells you what it thinks you entered, then tells you its answers.

We conclude that \(\sin 30^{\circ}=\frac{1}{2}\), \(\sin 60^{\circ}=\frac{\sqrt{3}}{2}\) and \(\sin 90^{\circ}=1\).

WA also provides us with decimal approximations to these ratios.

\(\sin 30^{\circ}=0.5\), \(\sin 60^{\circ}=0.866025\) and \(\sin 90^{\circ}=1\).

Try these

Exercise \(\PageIndex{1}\)

Find \(\sin \theta \), \(\cos \theta \), and \(\tan \theta\) for each triangle. Write your answers as decimal numbers rounded to 4 places.

1. 
2. 
3. 
4. 
5. 

Answer

1. \({\mathrm{sin} 45{}^\circ \ }=\frac{1}{\sqrt{2}}=0.7071,\ \)cos\(\ 45{}^\circ =\frac{1}{\sqrt{2}}=0.7071\), tan\(\ 45{}^\circ =1\)
2. \({\mathrm{sin} \theta \ }=\frac{4}{5}=0.8,\ \)cos\(\ \theta =\frac{3}{5}=0.6\), tan\(\ \theta =\frac{4}{3}=1.3333\)
3. \({\mathrm{sin} \theta \ }=\frac{\sqrt{5}}{3}=0.7454,\ \)cos\(\ \theta =\frac{2}{3}=0.6666\), tan\(\ \theta =\frac{\sqrt{5}}{2}=1.1180\)
4. \({\mathrm{sin} \theta \ }=\frac{2}{\sqrt{5}}=0.8944,\ \)cos\(\ \theta =\frac{1}{\sqrt{5}}=0.4472\), tan\(\ \theta =\frac{2}{1}=2\)
5. \({\mathrm{sin} \theta \ }=\frac{15}{17}=0.8834,\ \)cos\(\ \theta =\frac{8}{17}=0.4705\), tan\(\ \theta =\frac{15}{8}=1.875\)

Exercise \(\PageIndex{2}\)

Find each value. Write your answers as decimal numbers rounded to 4 places.

1. \(\sin 30^{\circ}\), \(\cos 30^{\circ}\), \(\tan 30^{\circ}\)
2. \(\sin 90^{\circ}\), \(\cos 90^{\circ}\)
3. \(\sin 0^{\circ}\), \(\cos 0^{\circ}\), \(\tan 0^{\circ}\)
4. \(\sin 180^{\circ}\), \(\cos 180^{\circ}\)
5. \(\sin 120^{\circ}\), \(\cos 120^{\circ}\)

Answer

1. \({\mathrm{sin} 30{}^\circ =0.5\ }\), cos\(\ 30{}^\circ =0.8661\), tan\(\ 30{}^\circ =0.5774\)
2. \({\mathrm{sin} 90{}^\circ =1\ }\), cos\(\ 90{}^\circ =0\)
3. \({\mathrm{sin} 0{}^\circ =0\ }\), cos\(\ 0{}^\circ =1\), tan\(\ 0{}^\circ =0\)
4. \({\mathrm{sin} 180{}^\circ =0\ }\), cos\(\ 180{}^\circ =-1\)
5. \({\mathrm{sin} 120{}^\circ =0.8660\ }\), cos\(\ 120{}^\circ =-0.5\)