5.2: Circular Trigonometry

Last updated
Save as PDF

Page ID: 125051

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

The Sine Function on the Unit Circle

In computer games, objects typically move up-and-down and left-to-right. These movements can be produced using the sine and cosine functions.

Draw a circle with radius 1 unit and on its circumference, place a point, let’s call it $P$.

The circle centered at the origin with radius 1 is called the unit-circle.

$This image shows a circle in the xy-plane with the center at (0,0) and a radius of 1. The radius ends at the end of the circle at point P which is (x,y).$

From our presentation of the sine and cosine function using right triangles, we can see that

\[\sin \theta=\frac{\text { opposite }}{\text { hypotenuse }}=\frac{y}{1}=y \nonumber \]

\[y=\sin \theta \nonumber \]

This tells us that the sine of the angle $\theta$ determines the vertical distance of the point $P$ from the horizontal axis.

$This image shows a triangle inside the first quadrant of a circle with a radius of 1. The opposite side of the triangle is the sine of theta. The sine of the angel theta equals the y-value of point P on the unit circle.$

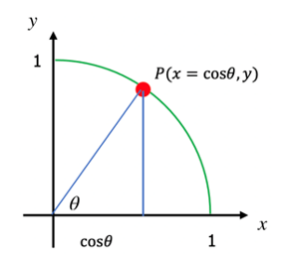
The Cosine Function on the Unit Circle

To define cosine function, place a point $P(x,y)$ on the circumference of unit-circle.

Once again, from our presentation of the cosine functions using right triangles, we can see that

\[\cos \theta=\frac{\text { adjacent }}{\text { hypotenuse }}=\frac{x}{1}=x \nonumber \]

\[x=\cos \theta \nonumber \]

This tells us that the cosine of the angle $\theta$ determines the horizontal distance of the point $P$ from the vertical axis.

$This image shows a triangle inside the first quadrant of a circle with a radius of 1. The adjacent side of the triangle is the cosine of theta. The cosine of the angel theta equals the x-value of point P on the unit circle.$

The Sine and Cosine Functions on any Circle

We can extend this idea by making the radius of the circle $r$ units rather than just 1 unit.

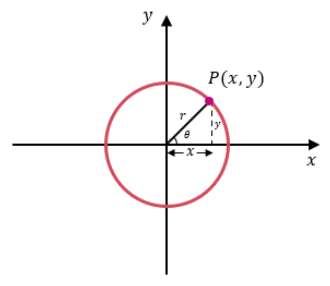
$Representation of Point P with coordinates x and y on the circle of any radius r. The circle has a right triangle inside of it. The triangle has the adjacent side x and the opposite side y. There is an angle of theta between the adjacent side and the hypotenuse.$

Using the same reasoning we just used with the unit circle, we see that

\[\sin \theta=\frac{\text { opposite }}{\text { hypotenuse }}=\frac{y}{r} \rightarrow r \cdot \sin \theta=y \rightarrow y=r \cdot \sin \theta \nonumber \]

\[\cos \theta=\frac{\text { adjacent }}{\text { hypotenuse }}=\frac{x}{r} \rightarrow r \cdot \cos \theta \rightarrow x=r \cdot \cos \theta \nonumber \]

which, again, tells us that the sine of the angle $\theta$ determines the vertical distance of the point $P$ from the horizontal axis and that the cosine of the angle $\theta$ determines the horizontal distance of the point $P$ from the vertical axis.

If $P$ represents an object, that object’s height $y$ off the ground (the horizontal axis) is given by $r\cdot \sin \theta $, and that object’s horizontal distance $x$ from some reference point is given by $r\cdot \cos \theta $. The height of the object is controlled by some number $r$ times $\sin \theta$, and its horizontal distance is controlled by some number $r$ times $\cos \theta$.

$This image shows a triangle inside the first quadrant of the circle. The radius of the circle is r, the opposite side is r times sine(theta) and the adjacent side is r times cosine(theta). Theta is the angle between the hypotenuse and the adjacent side. The r and r times cosine(theta) connect at the edge of the circle at point P, which is (x=r times cosine(theta),y=r times sine(theta)).$

Example $\PageIndex{1}$

An object lies on the circumference of a unit circle. Find its coordinates if the line segment from the origin to the object makes angle of 30° with the horizontal.

Solution

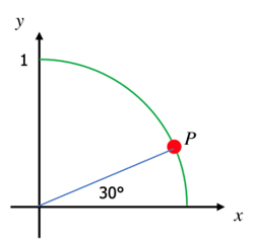
$This image shows the first quadrant of a circle with a radius of 1. There is a line connecting the center of the circle at (0,0) and the edge of the circle at point P. The line is 30 degrees away from the x-axis.$

Because the object is on the circumference of unit circle, we can use

$\begin{gathered}
x=r \cos \theta \text { and } y=r \sin \theta, \text { with } r=1, \theta=30 \\
x=1 \cos 30^{\circ} \text { and } y=1 \sin 30^{\circ} \\
x=\cos 30^{\circ} \text { and } y=\sin 30^{\circ} \\
x=0.8660 \text { and } y=0.5
\end{gathered}$

The coordinates of the object are (0.8660, 0.5).

Example $\PageIndex{2}$

An object lies on the circumference of a circle of radius 5 cm. Find its coordinates if the line segment from the origin to the object makes angle of 40° with the horizontal.

Solution

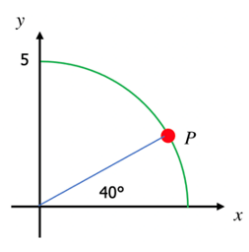
$This image shows the first quadrant of a circle with a radius of 5. There is a line connecting the center of the circle at (0,0) and the edge of the circle at point P. The line is 40 degrees away from the x-axis.$

Because the object is on the circumference of circle of radius 5 cm, we can use

$\begin{gathered}
x=r \cos \theta \text { and } y=r \sin \theta, \text { with } r=5, \theta=40^{\circ} \\
x=5 \cos 40^{\circ} \quad \text { and } y=5 \sin 40^{\circ} \\
x=5(0.7660) \text { and } y=5(0.6428) \\
x=3.8302 \quad \text { and } y=3.2139
\end{gathered}$

The coordinates of the object are (3.8302, 3.2139).

Example $\PageIndex{3}$

The coordinates of an object are (2.1, 3.6373). Find its distance from the origin.

Solution

We can use the Pythagorean Theorem, $a^2+b^2=c^2$, where $c$ is the hypotenuse, the radius of the circle in our case.

$\begin{aligned}
& 2.1^2+3.6373^2=r^2 \\
& 4.41+13.2300=r^2 \\
& 17.64=r^2 \\
& \sqrt{17.64}=\sqrt{r^2} \\
& 4.2=r
\end{aligned}$

We conclude that the object is about 4.2 cm from the origin.

Try these

Exercise $\PageIndex{1}$

An object lies on the circumference of a unit circle. Find its coordinates if the line segment from the origin to the object makes angle of 45° with the horizontal.

Answer: (0.7071, 0.7071)

Exercise $\PageIndex{2}$

An object lies on the circumference of a unit circle. Find its coordinates if the line segment from the origin to the object makes angle of 5° with the horizontal.

Answer: (0.9962, 0.0872)

Exercise $\PageIndex{3}$

An object lies on the circumference of a circle of radius 25 cm. Find its coordinates if the line segment from the origin to the object makes angle of 75° with the horizontal.

Answer: (6.4705, 4.8396)

Exercise $\PageIndex{4}$

An object lies on the circumference of a circle of radius 10 feet. Find its coordinates if the line segment from the origin to the object makes angle of 135° with the horizontal.

Answer: (-7.0711, 7.0711)

Exercise $\PageIndex{5}$

How high above the ground is an object that makes an angle of 60° with a 4-foot-tall observer’s eyes and is 35 feet away from that observer’s eyes? Round to two decimals place.

$This image shows the first quadrant of a circle with a triangle inside of it. The x-axis is labeled ground. There is a horizontal line crossing the circle labeled eye level that is 4 units above the x-axis, or 4ft above the ground according to the labels. The hypotenuse of the triangle is 35 feet and the hypotenuse is 60 degrees away from the eye level line. The opposite side of the triangle is a straight line that connects the edge of the circle and the eye level line. The adjacent side is a portion of the eye level line. Finally, there is a straight blue line that connects the eye level line to the ground line.$

Answer: 34.31 ft

Exercise $\PageIndex{6}$

The coordinates of an object are (5.682, 2.0521). Find its distance from the origin if it makes an angle of 60° with the horizontal.

Answer: 6 units

Search

Text Color

Text Size

Margin Size

Font Type

Example \(\PageIndex{1}\)

Solution

Example \(\PageIndex{2}\)

Solution

Example \(\PageIndex{3}\)

Solution

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)