5.4: Graphs of the Cosine Function
- Page ID
- 125053
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Discrete Graph of the Cosine Function from 0° to 360°
Just as the sine function determines the vertical distance of an object from an observer, the cosine function determines the horizontal distance of an object from that observer.
Here is table of values for the cosine function for angles between 0° and 360° followed by a graph of the cosine function for all angles from 0° to 360°.
| Angle \(\theta\) | Cosine \(\theta\)(Horizontal Distance from Observer) |
|---|---|
| 0\(\mathrm{{}^\circ}\) | 1 |
| 45\(\mathrm{{}^\circ}\) | 0.7071 |
| 90\(\mathrm{{}^\circ}\) | 0 |
| 135\(\mathrm{{}^\circ}\) | –0.7071 |
| 180\(\mathrm{{}^\circ}\) | –1 |
| 225\(\mathrm{{}^\circ}\) | –0.7071 |
| 270\(\mathrm{{}^\circ}\) | 0 |
| 315\(\mathrm{{}^\circ}\) | 0.7071 |
| 360\(\mathrm{{}^\circ}\) | 1 |
The positive cosine values indicate that the object is to the front of the observer whereas the negative values indicate that the object is to the back of the observer. For example, at an angle of 45° from the observer’s eye, the object is 0.7071 units in front of the observer. At an angle of 135° from the observer’s eye, the object is 0.7071 units behind the observer.
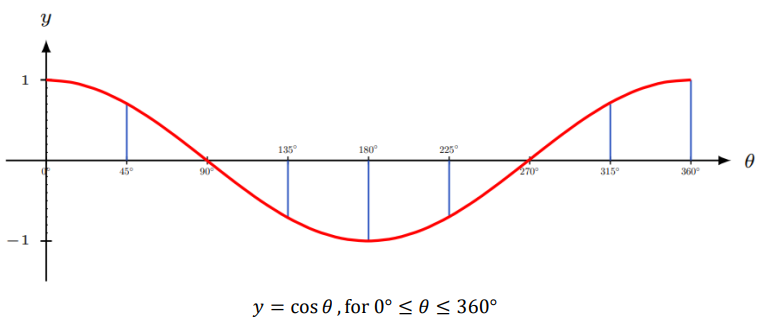
If you think that this graph looks like the graph of the sine function, but shifted to the left by 90°, you would be right.

The Extended Cosine Curve
Just as the sine curve does, the heights of the cosine curve oscillate between –1 and 1.

The graph of the cosine function gives a visual illustration of how it determines the horizontal distance of an object from a vertical axis.
It may now be visually apparent that
The cosine function determines the horizontal distance of an object to the left or right of an observer.
What to See
The graph shows how an object’s horizontal distance from the observer changes as the angle of view increases. As the angle of view increases, the horizontal distance from the vertical increases (moves away from the observer) and decreases (moves toward the observer).
What Not to See
The graph does not show how an object moves vertically as angle of view increases. The object is not moving along the curve.
Try these
An object moves along the circumference of a unit circle. Find its horizontal distance from an observer if the angle it makes from observer’s eye is
- 225°
- 270°
- 315°
- 360°
- Answer
-
- -0.7071
- 0
- 0.7071
- 1
An object moves along the circumference of a unit circle. Find its horizontal distance from an observer if the angle it makes from observer’s eye is
- 390°
- 405°
- 420°
- 450°
- Answer
-
- 0.8660
- 0.7071
- 0.5
- 0
Determine if each statement is true or false.
- Horizontal distance at 87° > Horizontal distance at 78°
- Horizontal distance at 45° > Horizontal distance at 145°
- Horizontal distance at 30° ≥ Horizontal distance at 150°
- Horizontal distance at 90° = Horizontal distance at 270°
- Answer
-
- False, since 0.0523 \(\mathrm{<}\) 0.2079
- False, since 0.7071 \(\mathrm{<}\) 0.9063 (Be careful here: 0.7071 \(\mathrm{>}\) –0.9063, but the negative sign tells us the object is the left of the observer. Think absolute value. At 45\(\mathrm{{}^\circ}\), the object is 0.7071 to the right of the observer. At 145\(\mathrm{{}^\circ}\), the object is 0.9063 units to the left of the observer, and, therefore, farther from the observer.)
- False, since is 0.8660 =-0.8660
- True, since 0 = 0

