2.2: Numeration Systems
- Page ID
- 70303
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In this exercise set, you will learn about two ancient numeration systems –those of the Chinese and Mayans.
Chinese Numerals
Chinese numerals are still used today. Symbols for some Chinese numerals are shown below.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 100 | 1,000 |
 |
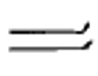 |
 |
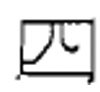 |
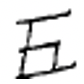 |
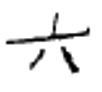 |
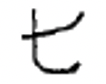 |
 |
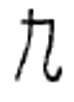 |
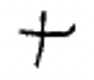 |
 |
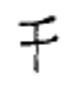 |
Chinese numerals are formed by writing the symbols vertically and using the multiplicative principle, which simplifies the recording of numerals by eliminating the repetition of symbols. For instance, the Chinese write the numeral for 3,058 by thinking \(3 \times 1000 + 5 \times 10 + 8\) and write down the symbols 3, 1000, 5, 10 and 8 in that order to represent that number. Even though you can think of the 8 as \(8 \times 1\), the 1 is not written down. This Chinese numeral (3,058) is shown to the left. The Chinese numeral for 872 is shown to the right.
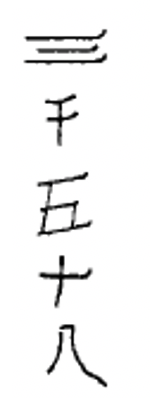
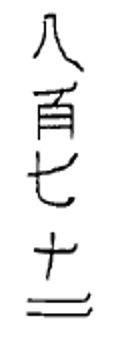
Below are some more Chinese numerals. Make sure you understand how to read all of them before trying the exercises.
| 6,400 | 87 | 9,531 | 2,605 | 4,011 | 7,000 |
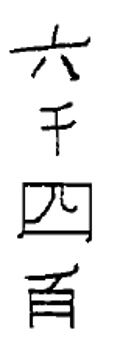 |
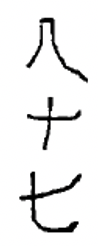 |
 |
 |
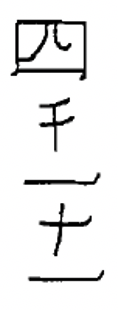 |
 |
Write each Hindu-Arabic numeral as a Chinese numeral.
- 5,093
- 610
- 427
- 8,008
So you won't have to keep turning back the page to remember these symbols, here again are the Chinese numerals you probably need to look at to do the following exercise.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 100 | 1000 |
 |
 |
 |
 |
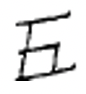 |
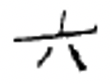 |
 |
 |
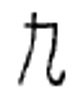 |
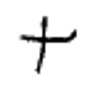 |
 |
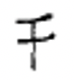 |
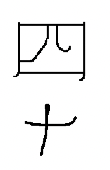
Rewrite each Chinese numeral in Hindu-Arabic numeral .
| a. ____ | b. ____ | c. ____ | d. ____ | e. ____ |
 |
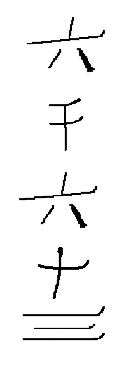 |
 |
 |
 |
Notice in the Chinese system that numbers over nine have symbols written in pairs. To write 800, you must write the symbol for 8 above the symbol for 100. IMPORTANT NOTE: This is true even if there is only a "1" in the place value, see 2d above. You MUST remember to write the symbol for "one" above the symbol for "ten"! Although the multiplicative principle allows you to write down fewer symbols than a simple additive system (for most numerals, at least), a further simplification would allow us to skip writing the second numeral of each pair. This would work if we used the position of the symbol to indicate the size of that group (10, 100, 1000, etc.) This type of system is called a positional numeration system. In order to keep track of a position where no digit is used, a symbol for zero is necessary. Although the Chinese system doesn't need a symbol for zero, a circle was introduced to represent zero in the 1200's.
Mayan Numerals
The final system we'll learn about in this Exercise Set uses a positional system and is similar to the Chinese system in that the symbols for the numerals are written from top to bottom. Mayan Numerals were developed by the Mayan priests of southern Mexico and Central America around 300B.C. It is believed to be the earliest positional numeration system incorporating a zero and using it for a placeholder.
Some Mayan Numerals are shown below. Try to figure out the pattern and then fill in the missing numerals.
Explain what symbols are in this system, what they stand for and how the system works for at least the numerals one to nineteen.
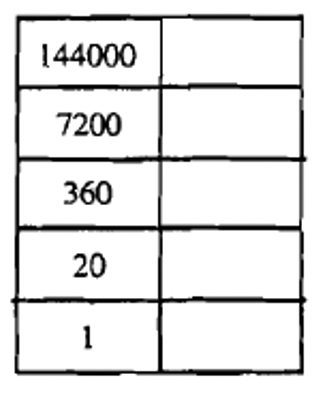
From what you have seen of this system so far, it might look like a simple additive system. One might guess that the numeral for 20 would be four line segments and that the numeral for 103 would be twenty line segments and three dots. At first glance, it is very similar to the tally system. However, the Mayans used a vertical positional system. The bottom level represented how many units (or ones), the second level up represented how many 20's, the third level up represented how many 360's (20 18), the fourth level up represented how many 7200's (20 18 20), the fifth level up represented how many 144,000's (20 18 20 20), etc. Except between the second and third level, each place value increased by a multiple of 20. It is almost a Base Twenty system except for that strange third level. Why the third level is 18 times the second level is explained later. Looking at the chart to the left, which shows the first four place values, may help you understand the system.
| 7200's |
| 360's |
| 20's |
| 1's |
To try and make sense of all of this, we will look at some Mayan numerals that have more than one position now. The numerals from one to nineteen only utilize the bottom level so it isn't apparent that the Mayan system is positional until you count past nineteen.
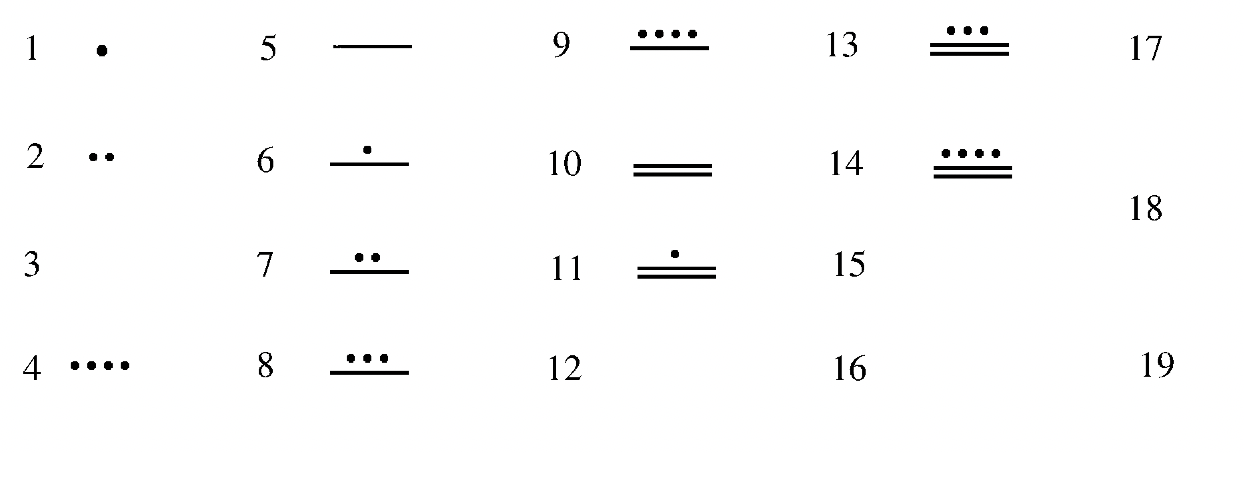
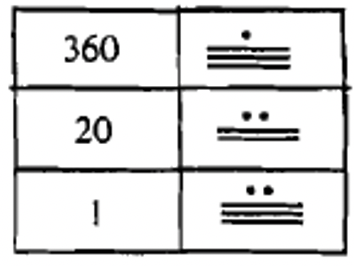
To the left is a two-level Mayan numeral. There is a 16 in the bottom level, representing 16 ones, or 16 (\(16 \times 1\)), plus there is a 7 in the second level up, representing 7 groups of twenty, or 140 (\(7 \times 20\)). We add the values of each level, 16 + 140, so the numeral you see represents 156.
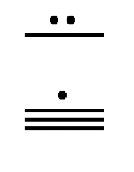
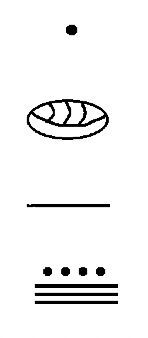
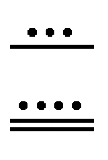
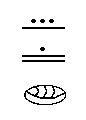
You have seen two basic symbols in this system so far –a dot ( ), which represents the number one and a line segment ( ), which represents the number five. As previously mentioned, there needs to be a symbol for zero to incorporate the use of place value. For that, the Mayans used a shell that looked something like this:
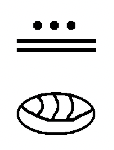
To the left is a two level Mayan numeral with a zero in the bottom level, representing zero ones, or 0, plus a 13 in the second level up representing 13 groups of twenty, or 260 (\(13 \times 20\)). So after adding the values together (0 + 260), the numeral you see represents the number 260.
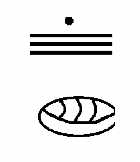
State the Hindu-Arabic equivalent of each Mayan numeral. Show how you obtained your answers. Note that proper space should be left between each place value. Otherwise, someone might incorrectly conclude the number shown for 5a represents 14, which would be the answer if there was no space.
| a. ____ | b. ____ | c. ____ |
 |
 |
 |
Now, we'll go on to some three and four level Mayan numeral. Remember that the place value for the third level up is 360 and the place value for the fourth level up is 7200. See if you can figure these out on your own first.
| a. ____ | b. ____ | c. ____ | d. ____ | e. ____ |
 |
 |
 |
 |
 |
How did you do? Make sure that if you still have any trouble understanding any of these that you go back and work through them again.
It's a little trickier to start with a Hindu-Arabic numeral and convert it to Mayan, but with a little patience and practice, you'll be doing it quickly and accurately! Before showing a method for doing this, try the following exercise. Hint: It should be easy, not hard –no calculator is required. Think about the place values of the various levels in the Mayan system.
Write the Mayan numeral equivalents for each of the following numbers:
| a. 1 | b. 20 | c. 360 | d. 7200 | e. 144000 |
To convert a number to a Mayan numeral, the first thing you'll have to determine is how many levels the numeral will have. Remember the levels: 1, 20, 360, 7200, 144000, 2880000, etc. So any numeral less than 20 has one level, a numeral between 20 and 359 has two levels, a numeral between 360 and 7199 has three levels, a numeral between 7200 and 143999 has four levels, and so on.
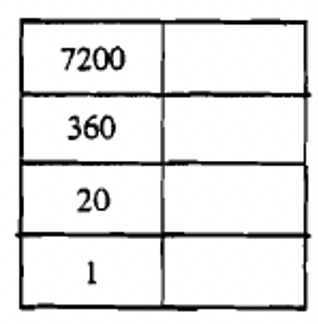
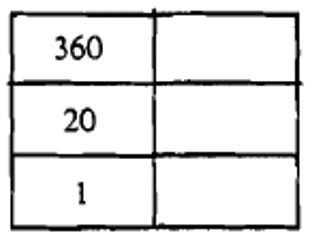
It might help if you set up a table with the correct number of levels set up already with a space to fill in what symbol you'll be using at each level. For instance, look below at the four most common charts you'll be using.
 |
 |
 |
 |
Let's start with the number 174. Convince yourself that this will be a two level numeral. We'll start at the top, which is the 20's place value. We have to ask ourselves how many 20's are in 174? This is a division question: \(174 \div 20 = 8\), remainder 14. We can begin to construct the Mayan numeral by starting with the two-level chart and filling an 8 in second level up as shown below.
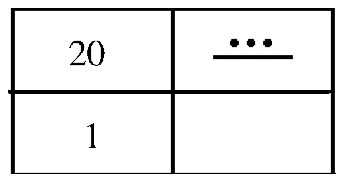
So far, we have eight groups of twenty, or 160 filled in, which leaves 14 more (the remainder) to accommodate. When you get down to the units place, the remainder is filled in there. So the next step is to fill 14 in the units place. Do that in the vacant place in the chart shown. Before feeling satisfied that everything is correct, check your answer by computing the Mayan numeral you have just constructed and see if it is indeed 174. Then, get rid of the chart and write the answer as a Mayan numeral as shown to the right.
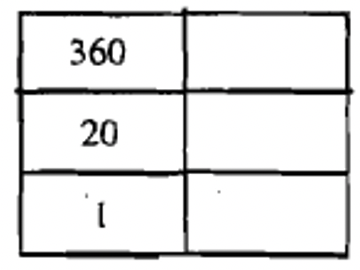
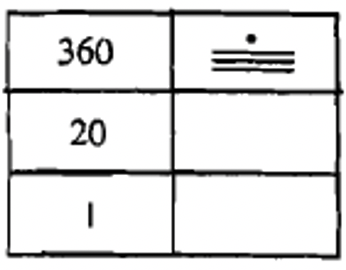
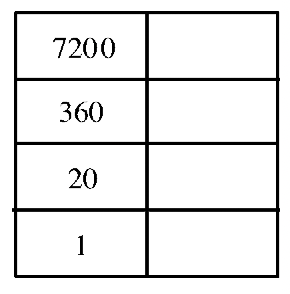
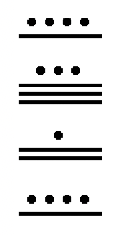
Let's try another number. We'll convert 6017 to a Mayan numeral. This will be a three level numeral, so we'll start off with a three level chart and figure out how many 360's are in 6017. We do this division problem: \(6017 \div 360 = 16\), remainder 257. This tells us to put the symbol for 16 in the third level up (360's place). Now we have to take the remainder, 257, and find out how many 20's there are in it to find out what to put in the second level. We do this division problem: \(257 \div 20 = 12\), remainder 17. Since only the units place value is left (the bottom level), the remainder of 17 goes in that level. The sequence of filling in the charts is shown below. Make sure you go back and check your work by converting the numeral back to Hindu-Arabic (\(1 \times 17 + 12 \times 20 + 16 \times 360\)) and seeing if it really equals 6017.
 |
 |
 |
 |
Before going on, I'm going to show you a quick and easy way to find out the quotient and remainder by using a simple calculator when doing these division problems. If you can already do it easily or your calculator figures it out for you, skip on down to Exercise 8. Let's say you were going to change the number 5263 to Mayan. The first division problem you would have to compute would be \(5263 \div 360\). When you do this on your calculator, it shows up something like 14.619444. This indicates that there are 14 360's in 5263, but the remainder isn't evident. At least, you know to put 14 in the third level up. To find the remainder on your calculator, key in 14 360 - 5263 and the number showing is the remainder if you ignore the negative sign! In this case, the remainder is 223. Remember that the remainder must be less than what you originally divided by –less than 360 in this case. If you wanted to find what to put in the 20's place, you would repeat this process by taking 223 (the remainder) and dividing it by 20. You might not need a calculator to continue. Let's try to find the quotient and remainder when dividing 24567 by 7200. On your calculator, \(24567 \div 7200 = 3.4120833...\) So the quotient is 3. To get the remainder, key in \(3 \times 7200 - 24567\), which gives a remainder of 2967 (which is less than 7200!). So the answer is 3, remainder 2967. To check, 7200 3 + 2967 must equal 24567. Think about why this process works and try it on the next few problems.
Use a calculator to find the quotient and remainder for these division problems.
- \(9876 \div 360\) = ____
- \(71509 \div 7200\) = ____
- \(333 \div 20\) = ____
- \(430040 \div 144000\) = ____
Let's convert 71509 to Mayan. Fill in the Mayan symbols on the chart to the left as we work through the problem. This is a four level Mayan numeral and Exercise 8b should help us get started! Did you get 9, remainder 6709? So 9 is in the fourth level up. Now, we compute: \(6709 \div 360 = 18\), remainder 229. So 18 is in the third level up. Next computation: \(229 \div 20 = 11\), remainder 9, so 11 is the second level up and that leaves 9 in the units place. The final answer is shown to the right.

Well, which number should we convert now? How about 430040 so we can use the help of Exercise 8d? Fill in the Mayan symbols on the chart to the left as we work through the problem. We first note that this is a five level Mayan numeral and so we do the division in Exercise 8d which gives a 2 at the fifth level up with a remainder of 142040. This is a big remainder but less than 144000. Now, we divide 142040 by 7200 to get 19 at the fourth level up and a remainder of 5240. Next, divide 5240 by 360 to get 14 at the third level up and a remainder of 200. There are exactly ten 20's in 200 and no remainder for the units, so we need to have a zero at the bottom level. Finally, the numeral we seek is shown on the right. Make sure you check it by computing \(2 \times 144000 + 19 7200 + 14 \times 360 + 10 \times 20 + 0!\) Does it really equal 430040? If so, it's right.

Let's convert 1584060 to Mayan. This is another five level Mayan numeral, so our first division of \(1584060 \div 144000\) gives us 11 at the fifth level up with a remainder of 60. There are no 7200's or 360's in 60, so there must be zeroes at those two levels. There are 3 20's in 60 with no remainder, so the units level must also have a zero. The numeral is shown on the right. Please check it. Is it really 1584060?
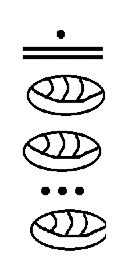
Think about the highest numeral value that can be on any given level. For instance, the bottom level could go up to 19, or . But what about the second level up? What number would be represented by a two level Mayan numeral if there was a 19 at the second level up and a zero at the bottom level? Write the Mayan numeral for 380.
What is the highest Mayan numeral value that should be on the second level up? What is the highest Mayan symbol that could be on any level except the second level up?
Convert each of the following to Mayan numerals. (show work) CHECK Answers!
- 1549
- 4750
- 53981
- 145804
- 1000000
You may be wondering why the Mayans chose 360 for the third level up instead of 400, which seems more natural. Their counting system was based on their calendar, which consisted of 18 months of 20 days each, hence 360. The extra five days were considered "useless" and they didn't worry about them. Their system made it easy to count time. They didn't count the "useless days." For instance, consider the following:
| a. 1 year | b. 2 years | c. 3 years | c. 5 months, 9 days | d. 8 years, 11 months |
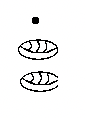 |
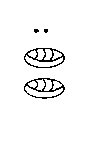 |
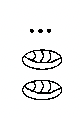 |
 |
 |
Write the Mayan numeral for the number of (non-useless) days in:
- 7 months, 15 days
- 13 Mayan years
- 20 Mayan years
The final exercise of this set will be to compare the Hindu-Arabic, Chinese and Mayan numerals.
State how many different symbols a person has to memorize to understand each system:
- Hindu-Arabic: _____
- Chinese: _____
- Mayan: _____
Write each number as a numeral in Chinese and Mayan. Note how many symbols it takes to write the given number in Hindu-Arabic, Chinese and Mayan. Show work.
- 15
- 100
- 100
- 9999


